基于二阶规则波模拟的数值波浪水槽优化

曾 诚,尹雨然,周 婕,邱 斐,白一墨,王玲玲

(1.河海大学水利水电学院,江苏 南京 210098; 2.河海大学力学与材料学院,江苏 南京 211100)

近年来,随着海洋资源的不断开发,海岸和近海工程受到社会各界的广泛关注。波浪作为海洋环境中的重要因素,对海洋工程结构的强度和稳定性具有重要影响。数值模拟作为一种研究手段,在工程应用中得到了越来越多的重视[1]。目前,波浪研究中较为常用的数值模型是基于Navier-Stokes方程的黏性流数值波浪水槽[2]和基于光滑粒子流体动力学的数值波浪水槽[3]。与物理波浪水槽[4]相比,数值波浪水槽具有成本低、信息完整和模拟能力强等优点。

数值造波和消波技术是数值波浪水槽构建的关键技术。常用的造波方法包括速度边界法[5]、推板造波法[6]和质量源造波法[7]等,消波方法主要包括辐射边界法、阻尼消波法和松弛区域法等。数值造波技术方面,徐刚等[8]采用速度边界法建立了数值波浪水槽,研究了波浪衰减特性,并对数值波浪水槽的模拟精度和波浪衰减问题进行了分析。Higuera等[9]利用OpenFOAM建立了三维多推板数值波浪水槽,成功模拟生成了二维和三维聚焦波。Prasad等[10]采用推板造波法建立了数值波浪水槽,并对波能转换器的性能进行了研究。Machado等[11]将推板和摇板2种造波方法进行了对比,认为推板造波法更准确。Lin等[12]将源造波法运用到基于Navier-Stokes方程的数值波浪水槽中,通过使用不同的源函数,产生各种波序列。为消除波浪水槽边界产生的反射波,保证水槽内波浪稳定,前人提出了多种消波方法。Milgram[13]在1970年最早提出了主动吸收造波理论。William等[14]在水槽末端设置斜坡来达到消波目的。Kim等[15]采用网格逐渐稀疏的消波方法建立了三维数值波浪水槽,产生了较好的消波效果。另外,还可采用出流边界使波浪完全透射过出流边界,从而避免发生波浪反射,其中Sommerfeld辐射边界[16]具有较好的消波效果。Clément[17]对Sommerfeld辐射边界条件进行了研究,指出由于该条件在时间和空间上是局部的,因此仅限于频率已知的规则入射波和长波情况,而不适用于完全非定常入射波情况。邹志利等[18-19]也对Sommerfeld辐射边界条件进行了研究,发现单独采用该条件的消波效果并不理想。Israeli等[20]提出了阻尼消波法,分析了消波系数对消波效果的影响,并尝试通过辐射边界条件和阻尼区消波相结合的方法提高消波效果。Baker等[21]在其二维边界元模式中引入阻尼消波法,其主要思想是在消波区域对自由面边界条件或动量方程添加一阻尼耗散项,从而达到消波的目的。随着阻尼消波法的不断发展和完善,该方法成为了数值波浪水槽研究中广泛运用的消波方法。Clément[17]指出,通过阻尼消波能够有效消除高频短波,但是对于低频长波消波效果不太理想,需要延长阻尼区域,增加计算成本。Méndez等[22]针对阻尼消波法进行了研究,结果表明阻尼消波区设置不合理会导致平均水位的缓慢抬升。韩朋[23]基于VOF方法针对不规则波的数值模拟进行了阻尼消波研究,给出了不同波要素组合情况下阻尼系数的经验取值范围。王国玉等[24]基于OpenFOAM求解器interDyMFoam,开发了数值波浪水槽,并将计算结果与试验测量数据进行对比,验证了数值造波和消波方法的可靠性。另外,Tian等[25-26]给出了阻尼项的不同表达形式。近年来,Jacobsen等[27]提出了松弛区域法,在波浪水槽前后端设置松弛区域,通过合理分配计算值和理论值之间的权重实现数值解与解析解之间的过渡,从而达到消波效果。田康等[28]基于OpenFOAM建立数值波浪水槽,并通过二次开发引入松弛区域法,取得了较好的消波效果。

基于上述文献综述,前人对非线性波模拟的数值波浪水槽优化设置研究较少,本文基于CFD开源软件包OpenFOAM建立了二维黏性流数值波浪水槽,综合考虑不同波陡工况下(i=0.01～0.06)Stokes二阶波的模拟精度和计算成本,从造、消波方式选择、网格划分、紊流模型选择等方面对数值波浪水槽进行全面优化,以期提高非线性波模拟的精度和效率。

1 数学模型

1.1 基本两相流控制方程

基本两相流控制方程主要包括不可压缩流体的连续性方程(式(1))、动量守恒方程(式(2))以及基于体积函数(volume of fluid,VOF)法的相方程(式(3))。

∇·U=0

(1)

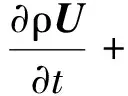
(2)

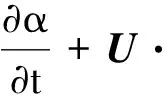
(3)

式中:U=(u,w)为笛卡尔坐标系下的流速场;ρ为整个流场的密度;μ为动力黏滞系数;g=(0,-9.81)为重力加速度;p为压力场;α为水的体积分数。

当α=1,表示网格单元内全部为水,当α=0,表示网格内全为空气,当0<α<1,代表该网格单元内存在自由液面。通过对α的迭代求解,可根据式(4)进一步确定网格单元内其他的特性参数。

φ=αφW+(1-α)φA

(4)

式中:φ为网格内其他参数,如密度、分子黏性系数等;下标W表示水,A表示空气。

本文采用k-ωSST紊流模型封闭控制方程,采用PIMPLE算法进行速度-压力解耦。其中,时间项采用一阶隐式格式离散,对流项和黏性项采用二阶迎风格式离散,压力项、紊动能和耗散率项采用二阶中心差分格式进行离散。

1.2 造波方法

1.2.1 推板造波法

在数值波浪水槽中采用推板造波法时,推板冲程S与目标波高H的关系为

(5)

其中k=2π/L

式中:k为波数;L为波长;d为初始水深。

本文模拟的波浪中包括深水(水深大于波长一半)和有限水深(水深和波长关系为0.5>h/L>0.05)条件下的有限振幅波,因此采用Stokes非线性波理论。根据Madsen[29]造波理论,采用修正后的推板位移公式产生稳定的Stokes二阶波:

(6)

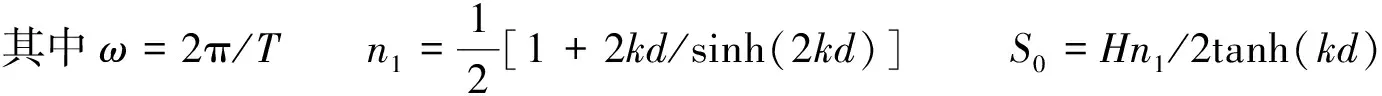
式中:xp为推板冲程;ω为圆频率;T为波浪周期;t为时间。

本文理论解采用Stokes二阶波波面方程:

(7)

式中x为沿波浪传播方向的坐标。

1.2.2 速度边界法

采用速度边界法造波时,通过控制边界处的水平和垂向速度产生目标波形,水平速度u和垂向速度w分别为

(8)

(9)

式中z为沿水深方向坐标,向上为正。

1.3 消波方法

1.3.1 阻尼消波法

阻尼消波的原理为在动量方程中加入阻尼项,在数值水槽消波段实现动量衰减,从而消除边界上的反射波,在式(2)中加入阻尼项ρθU后,动量方程如下:

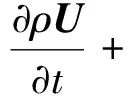
(10)

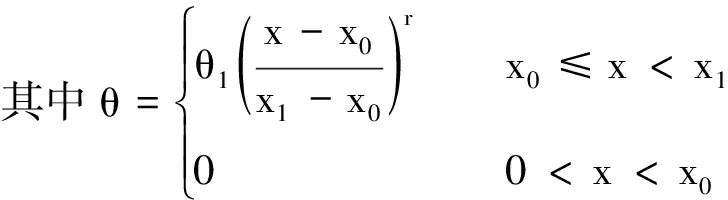
式中:x0为消波段起点;x1为消波段终点;θ为阻尼函数,常用的阻尼函数形式包括线性形式(r=1)和平方形式(r=2);θ1为阻尼系数;r为阻尼项指数。

1.3.2 辐射边界法

在水槽末端施加适当的辐射条件,能使波浪在出口边界处无干扰或干扰很小的传播出去。Sommerfeld辐射边界条件的定义如下:

(11)

式中Cu、Cw分别为u和w在出口边界处的值。

1.3.3 松弛区域法

在数值波浪水槽首端设置松弛区域可以有效消除计算区域内部的波浪反射对入口的影响,在水槽末端设置松弛区域能够防止出口边界产生反射波,对研究区域产生影响。松弛区域法消波原理是在松弛区域内引入一个消波因子αR:

(12)

式中XR为消波因子的局部坐标。

XR轴正方向始终指向计算域外,这样使得消波因子在靠近流体内部一侧的变化非常缓慢,从而达到减少反射的目的。在松弛区域内,流速和体积分数等物理量(φ)由计算值(φc)和解析解(φa)加权得到:

φ=αRφc+(1-αR)φa

(13)

2 模型建立

2.1 模型区域设置

本文建立的二维数值波浪水槽计算区域、计算边界及松弛区域内松弛因子分布如图1所示。水槽模型长度为6倍波长以上,其中造波区长度为5m,研究区长度为4～5倍波长,消波区为1～2倍波长,采用松弛区域法消波时,进口松弛区域长度为5m,根据初步模拟结果,出口松弛区域为1倍波长较为合理。模型顶部设置为大气边界,左侧边界为造波边界,水槽底部设置为无滑移壁面,出口边界根据消波方法的不同分别设置为无滑移壁面或辐射边界。

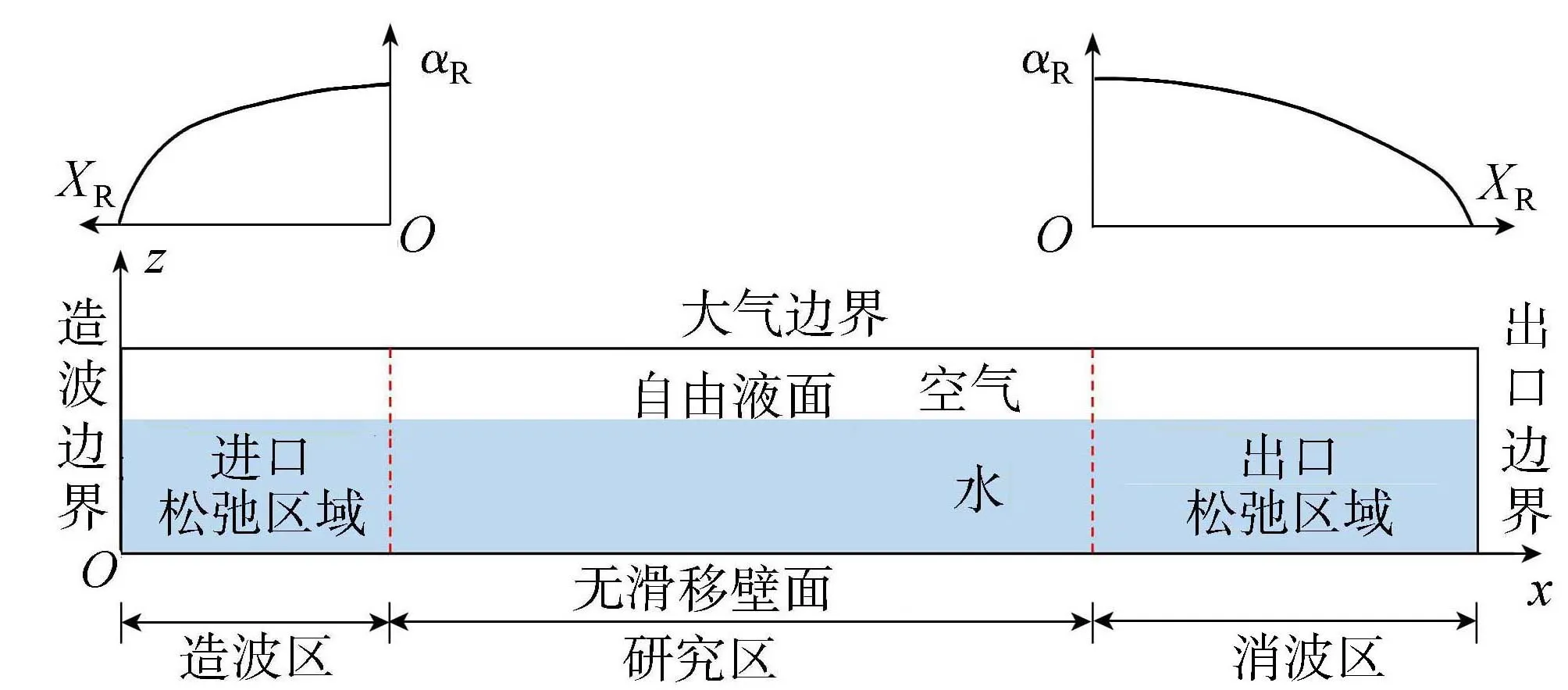
图1 数值波浪水槽示意图

2.2 网格无关性分析

为保证模拟精度,本文选取三套网格进行网格无关性分析,具体网格参数见表1。目标波高设置为H=0.1m,波长L=5.03m,采用推板造波,基于平方形式的阻尼函数消波。三套网格的计算结果如图2所示。由图2可知,mesh1的模拟值与理论值相差较大,模拟精度较低,而mesh2和mesh3的模拟结果相近,并且十分接近理论值,都能达到较高的模拟精度。为保证模拟精度的同时还节省计算资源,后续计算采用mesh2的网格设置方式,并且在波面附近进行网格加密,以达到更好的模拟效果。三套网格及后续模型的计算时间均为20T,计算时间步长取T/1000。

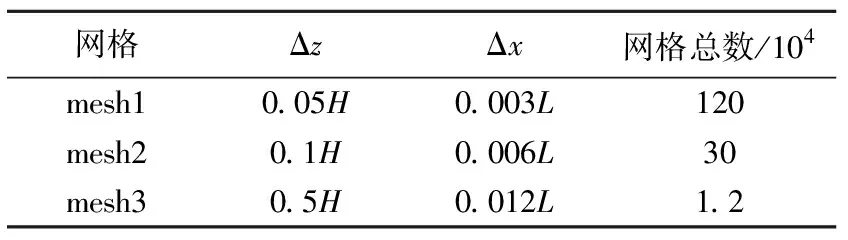
表1 网格参数

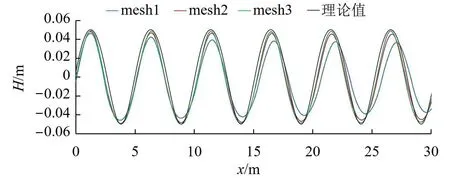
图2 不同网格下的沿程波面

2.3 紊流模型对比

为比较紊流模型对黏性流数值波浪水槽计算结果的影响,本文对比分析了目前比较常用的k-ε紊流模型和k-ωSST紊流模型,模拟的波浪参数及采用的造波、消波方法与第2.2节相同。由图3可知,k-ωSST紊流模型的模拟精度更接近理论值,而k-ε紊流模型的计算结果与理论值的偏差相对较大,波浪衰减较为明显。因此,本文后续计算中均选择k-ωSST模型。

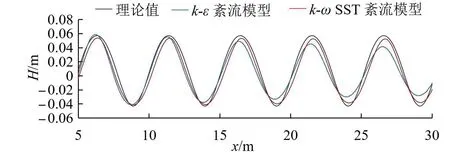
图3 不同紊流模型的沿程波面模拟结果

3 计算结果分析

3.1 工况设置

本文对6种不同波陡的Stokes二阶波进行模拟计算,波陡范围为0.01～0.06。各工况的波浪参数及模拟计算中采用阻尼消波法时的θ1见表2。由表2可知,θ1随着i的增大而增大。

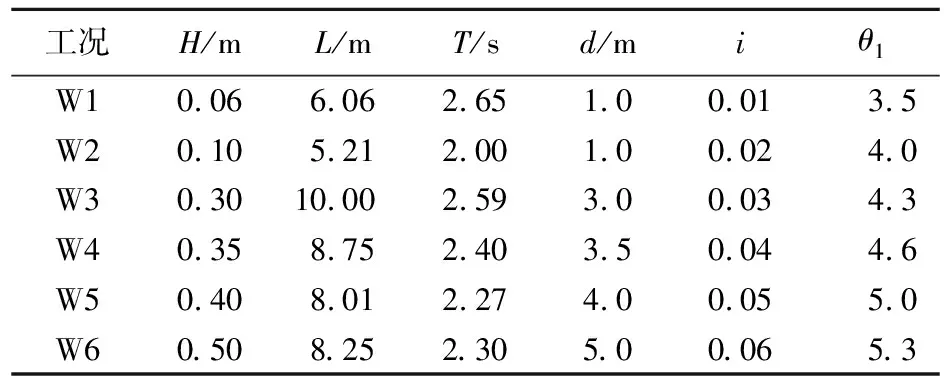
表2 波浪参数

3.2 消波效果

对表2中所示不同波陡工况,采用推板造波法产生Stokes二阶波,分别采用辐射边界法、阻尼消波法和松弛区域法进行模拟计算,对其消波效果进行对比分析。其中,在采用阻尼消波法时,对采用线性形式阻尼函数(r=1)和平方形式函数(r=2)的消波效果进行对比分析。本文采用Ursell等[30]提出反射系数定量评价消波效果,一般认为反射系数在5%以内可以满足消波要求。

由表3可知,阻尼消波的2种阻尼函数形式的反射系数均在5%以内,都具有较好的消波效果,但是随着波陡的增加,平方形式的阻尼函数优势变得更加明显。而采用辐射边界法的消波效果仅仅在波陡较小的情况下(i=0.01和i=0.02),反射系数才满足要求,而在其他波陡情况下(i=0.03～0.06),反射系数均大于5%,采用松弛区域法计算得到的反射系数均保持在较小的水平,但是在大波陡工况下,松弛区域法不如平方形式的阻尼函数优势明显。在不同波陡情况下,线性形式和平方形式的阻尼函数能够保证较好的消波效果,而平方形式的阻尼函数相较于线性形式,消波效果上更有优势,并且从阻尼在消波区域内的分布来看,平方形式的阻尼函数更有利于保证研究区域内的模拟精度,阻尼分布更加合理。后续进行造波效果分析时,消波方法均采用基于平方形式阻尼函数的阻尼消波法。

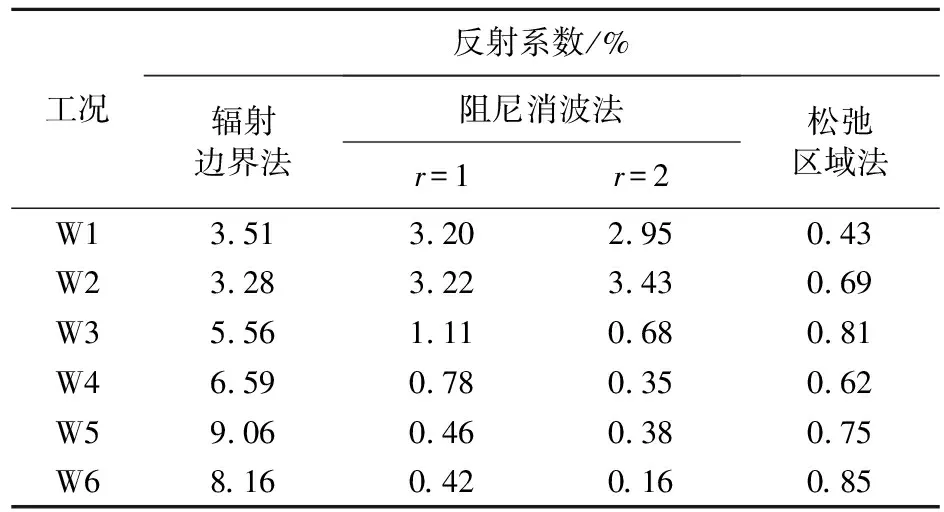
表3 反射系数计算结果

3.3 造波效果

为对模型造波效果进行对比分析,对表2中所示不同波陡工况分别采用推板造波法和速度边界法进行Stokes二阶波的模拟计算,消波方法均采用基于平方形式阻尼函数的阻尼消波法。针对不同工况计算结果,由于所计算的工况波高差距较大,为了得到更合理的误差分析结果,首先将计算值与理论值通过min-max标准化方法进行归一化处理,再分别计算不同工况下的均方根误差,计算结果见表4。

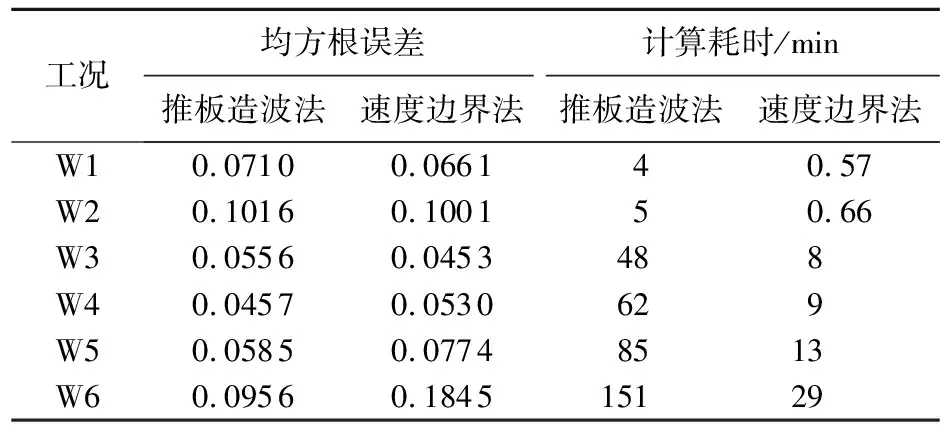
表4 均方根误差及计算耗时

由表4可知,在波陡较小的情况下,波浪的非线性较弱,利用速度边界法具有较高的模拟精度,在波陡为0.01的情况下,速度边界法的模拟精度高于推板造波法。但是随着波陡的增加,波浪的非线性逐渐增强,速度边界逐渐变得不适用,模拟精度逐渐低于推板造波法。在波陡为0.05和0.06时,2种造波方法产生的波浪与理论值的均方根误差相差较大,在模拟精度上推板造波法的优势较为明显。

本文的模拟计算在河海大学高性能计算平台上进行,每个工况利用48核心并行计算,CPU类型为2颗Intel Xeon 6240R(24核2.4GHz)。虽然推板造波能够产生较为精确的波形,但是在计算时间方面,采用推板造波法的计算耗时是速度边界法的5～8倍,尤其是在波陡较大,所需网格数量较多的情况下,计算耗时的差别会更加明显(表4)。

图4为6种波陡工况下,采用2种造波方法的沿程波面计算结果与理论值的对比。波陡过小或过大都不容易产生与理论值吻合程度较高的结果。在小波陡工况(W1和W2)下,虽然计算值与理论值的均方根误差表现较小,但是在波形方面,2种造波方法所产生的波浪与理论值都存在一定的偏差,而此时速度边界法所产生的波形在精度方面较有优势。在大波陡工况(W5和W6)下,波浪非线性较强,速度边界法的优势不明显,推板造波法具有较高的精度。此外,在W3和W4工况下,2种造波方法所产生的波形与理论值吻合较好,采用速度边界法和推板造波法均能达到较高的模拟精度。

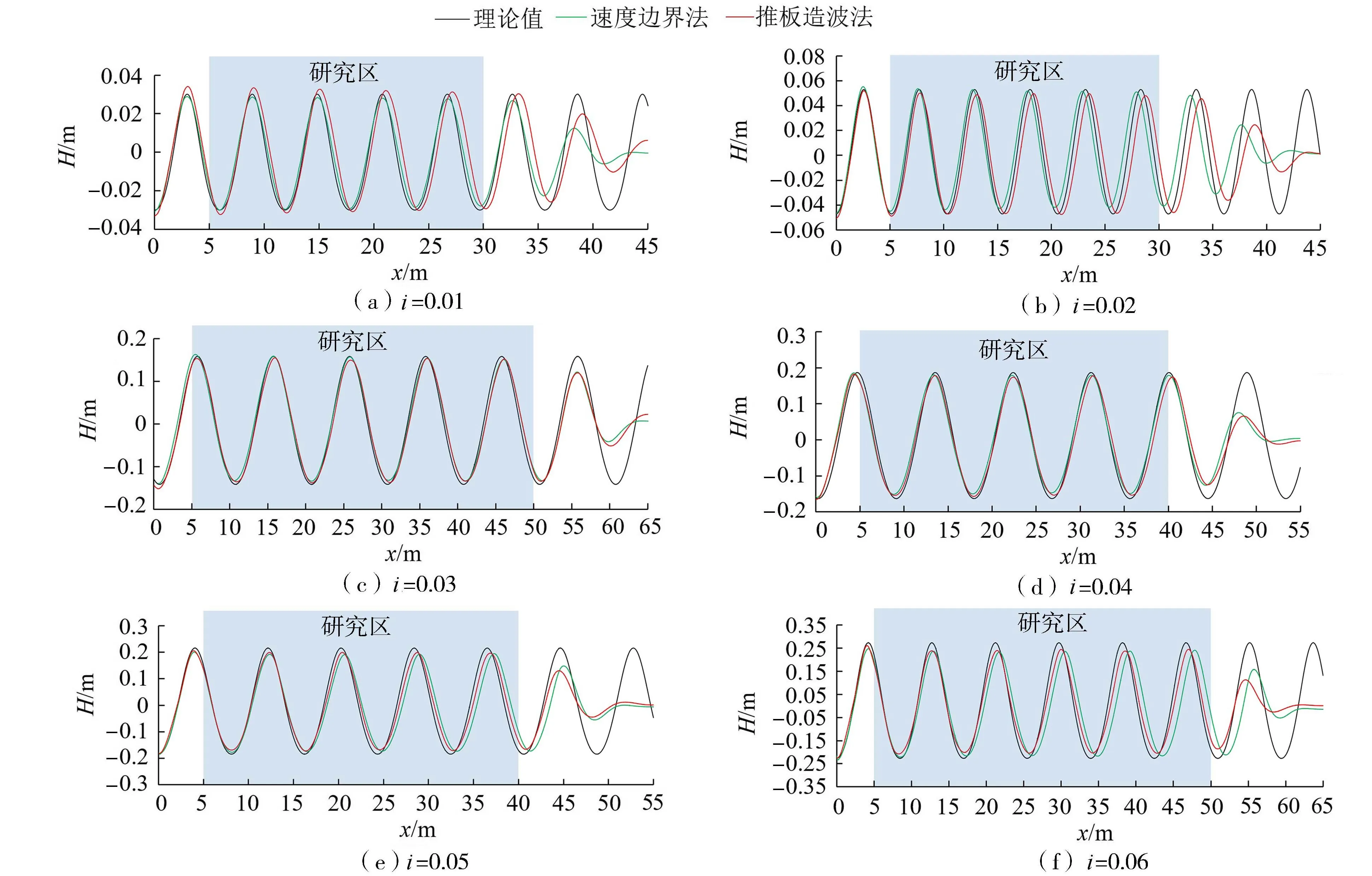
图4 不同波陡条件下水槽内波高

为分析推板造波法和速度边界法所产生的波浪随时间变化的情况,在距离水槽造波边界2倍波长处设置监测点,监测波高随时间变化的情况。图5为采用2种造波方法达到稳定波高的时间序列(15s后)与理论值的比较情况。由图5可知,采用2种造波方法时监测点处波面历时曲线与理论值基本吻合,表现为小波陡工况(W1、W2和W3)下吻合程度较高,大波陡工况(W4、W5和W6)下吻合较差,误差主要体现在波峰处。另外,随着计算时间的增长,采用速度边界法和阻尼消波法的组合方式时出现了较为明显的水面抬升现象,如图5(b)～(f)所示。波陡越大,水面抬升越明显,在W6工况(i=0.06)下,波面最大约抬升了波高的10%。出现水面抬升现象的原因是由于大波陡工况下,波浪的非线性较强,在一个波浪周期内边界上输入与抽取的速度不等,会引起质量守恒方面的问题,随着计算时间的增加,就产生了波面抬升问题[31]。然而,采用推板造波法和阻尼消波法的组合方式时,在各个波陡工况下,均能保持波面稳定,没有出现水面抬升现象。

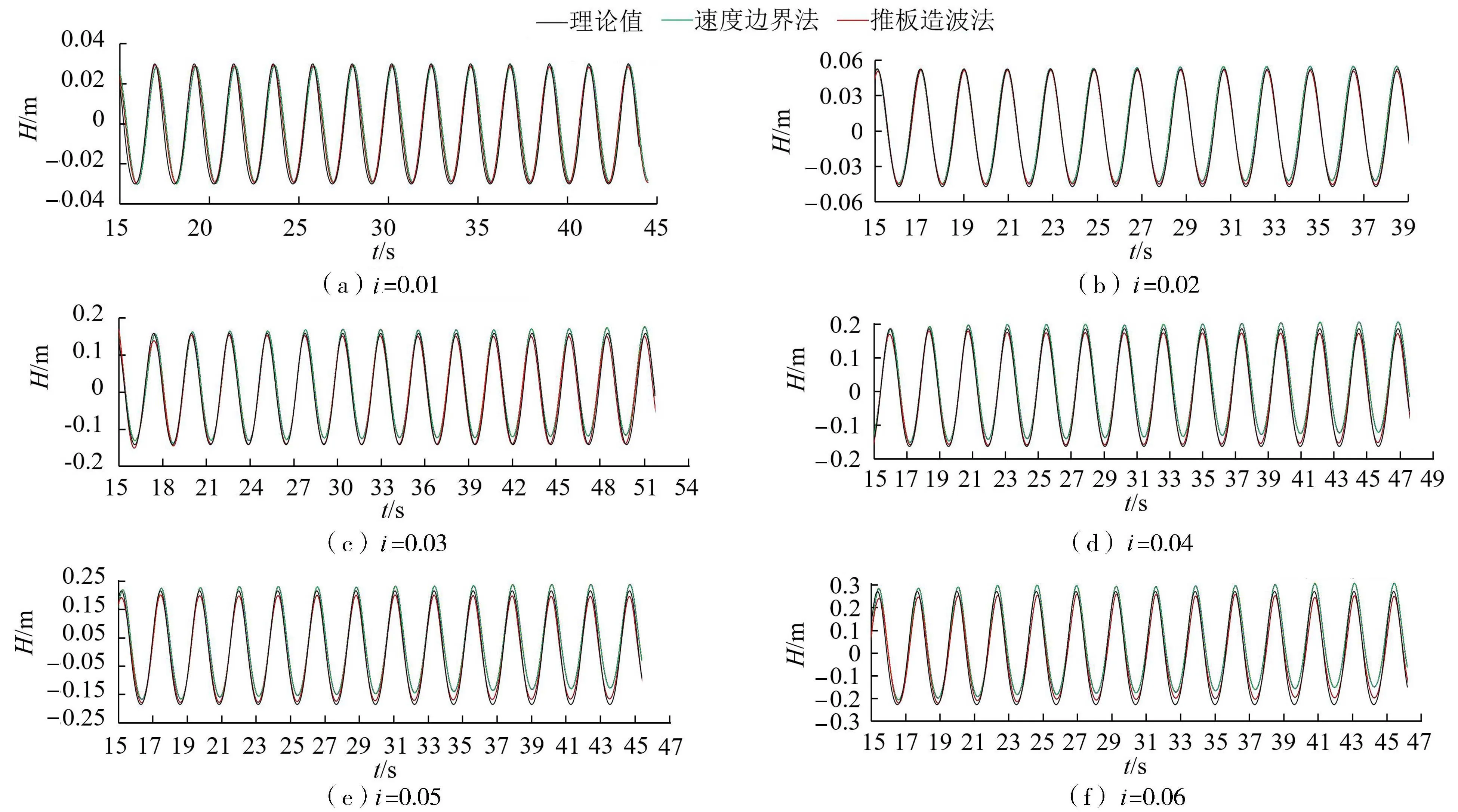
图5 不同波陡条件下x=2L处波面历时曲线

在进一步的模拟研究中发现,模拟非线性较强波浪时,如采用速度边界法造波,则必须采取相应的修正措施。例如,采用松弛区域法,在数值水槽的前后端添加松弛区,既能保证质量守恒又消除了二次反射波。图6为大波陡工况(i=0.06)下采用速度边界法造波时,分别采用阻尼消波法和松弛区域法消波的计算结果与理论值的波面历时曲线对比,从图6可看出,松弛区域法能够有效避免波面抬升现象,模拟结果与理论值符合较好。

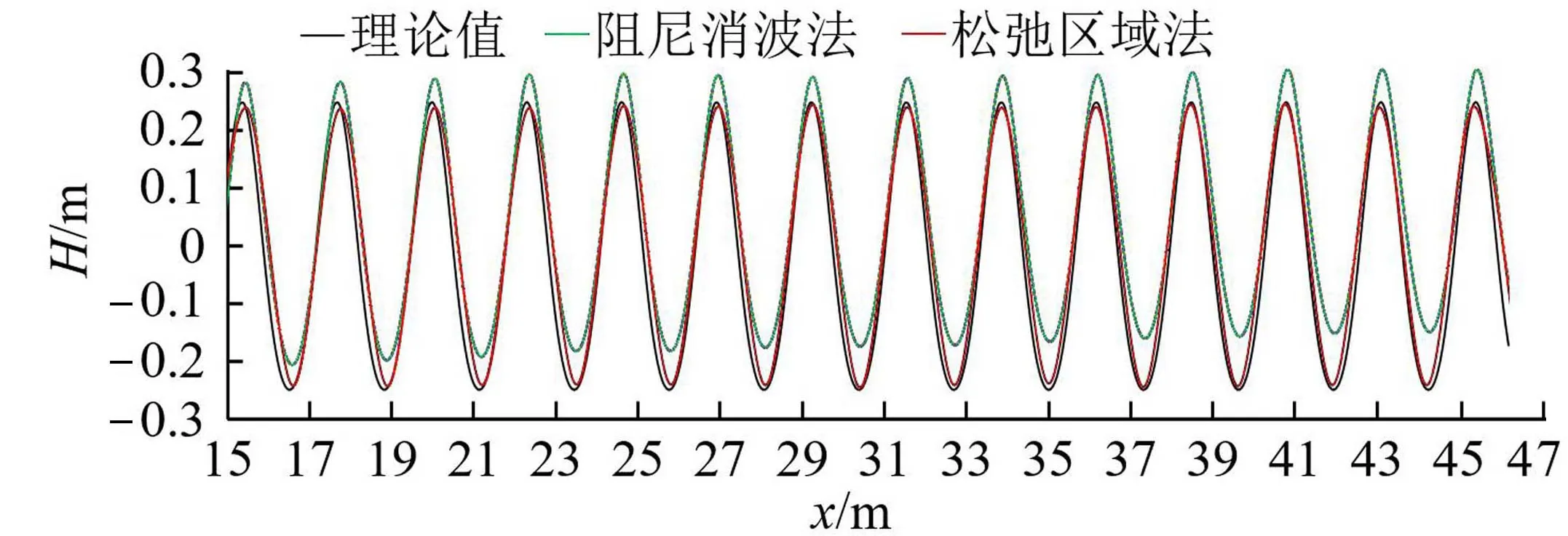
图6 大波陡工况(i=0.06)时速度边界法修正效果对比

4 结 论

a.消波效果方面,采用基于平方形式阻尼函数的阻尼消波法具有较好的消波效果。采用松弛区域法可有效消除大波陡工况下采用速度边界法导致的水面抬升现象。

b.造波效果方面,速度边界法在小波陡工况下模拟精度较高,计算耗时较少。推板造波法在大波陡工况下模拟精度较高,波形稳定性较好。

c.根据本文二阶规则波的数值模拟计算结果,对于小波陡(i=0.01～0.03)工况采用速度边界法造波和松弛区域法消波的组合方式具有较高的模拟精度,对于大波陡(i=0.04～0.06)工况采用推板造法造波和基于平方形式阻尼函数的阻尼消波法消波的组合方式具有较高的模拟精度。