基于ABC-BP神经网络的地铁盾构地表沉降预测

朱 诚, 王昭敏, 隆 锋, 李福东, 丰土根, 张 箭

(1.河海大学岩土力学与堤坝工程教育部重点实验室,江苏 南京 210098;2.中交第二公路勘察设计研究院有限公司,湖北 武汉 430058;3.中交隧道工程局有限公司,北京 100102; 4.中交二公局第四工程有限公司,河南 洛阳 471013)

地铁盾构施工主要在繁华市区,下穿、侧穿地面较多建(构)筑物及管线,施工条件复杂。目前,盾构施工通过地表沉降监测来掌握开挖时周边变形情况,但由于监测频率较低及地表沉降监测存在一定滞后性,无法实时获取地表沉降以评价相应掘进参数调整的合理性。因此,对地表沉降实时预测及根据预测结果提前调整施工参数至关重要。

盾构施工地表沉降预测方法主要包括经验公式[1]、随机统计模型[2]及数值模拟方法[3]等。经验公式主要采用peck公式、有限单元法、随机介质理论等。随机统计模型主要有回归分析模型、时间序列模型和灰色模型。回归分析模型通过拟合数学表达式进行地表沉降预测;时间序列模型通过历史数据预测未来变化趋势;灰色模型则以时间序列出发,寻找因素之间的关系,依次累加实现非线性到线性的转化,从而预测地表沉降。数值模拟通过分析地层参数与掘进参数对地表沉降的影响,进而预测不同地层条件与掘进参数对应的地表沉降量。上述方法均存在一定的局限性,如:经验公式需要针对不同地区提出修正公式;数值模拟计算依赖于地层力学参数与本构关系的正确选取;时间序列预测模型无法反映地表沉降与地层条件之间关系,预测精度依赖于历史数据等。

近年来,随着我国大数据和5G技术的发展[4-8],结合人工智能解决城市隧道盾构工程问题已成为必然趋势。随着人们对神经网络的应用研究越来越深入,各类人工智能优化算法得到突飞猛进的发展[9],采用机器学习方法对盾构地表沉降预测成为主流。林广东等[10]基于时空特征区域神经网络对隧道地表沉降进行预测,预测值与实际值趋势基本一致;易黄智等[11]基于遗传算法GA优化BP神经网络,构建了GA-BP神经网络进行变形预测,具有较高的预测精度及稳定性;刘春梅等[12]采用K均值聚类算法改进RBF神经网络用于基坑开挖地表沉降预测分析,具有较好的预测精度;乔金丽等[13]采用变步长方法筛选影响地表沉降因素,构建BP神经网络进行预测,预测结果与实测结果一致;郭子奇等[14]采用粒子群算法(PSO)优化BP神经网络,构建基于PSO-BP神经网络的土体参数与地表沉降预测模型;陈柚州等[15]基于人工蜂群算法ABC优化小波神经网络,并对地铁隧道沉降进行了预测;宫思艺等[16]通过构建BP-SVR模型预测距开挖面不同距离处的地面沉降量,具有较高预测精度;任松等[17]基于遗传算法GA优化的BP神经网络预测了隧道开挖时的地表沉降。

目前人工神经网络能够很好地预测地表沉降,许多学者通过构建BP神经网络对盾构地表沉降进行预测,并采用优化算法优化BP神经网络以提高预测精度。在此基础上,实现通过神经网络预测模型指导现场施工,开展以沉降控制为目标的盾构掘进参数选取指导是研究的最终目的。鉴于此,本文同时考虑地层参数和盾构掘进参数两类影响地表变形的因素,构建了采用人工蜂群(artificial bee colony,ABC)算法优化的地表变形BP神经网络预测模型(以下简称“ABC-BP神经网络模型”),并结合现场连续3个断面地表变形数据,研究盾构掘进地表变形全过程演变规律,提出了适用于指导施工的神经网络应用思路,以期实现施工前的超前预测,为该类工程的安全保障提供参考。

1 ABC-BP神经网络模型

1.1 BP神经网络模型

BP神经网络具备良好的非线性映射能力、自学习适应能力和并行信息处理能力,主要由输入层、隐含层、输出层组成。输入层输入信号通过连接权传递至隐含层再传递至输出层,实现输入信号的输出。如果输出值与希望输出值间的误差超出期望范围,则通过反向传播算法更新修正连接权,再正向传播输出。正向传播与反向传播反复进行,直至输出希望值,完成网络训练学习,即可用于预测分析。

BP神经网络反向传播采用梯度下降法,使误差函数达到最小值。BP算法易陷入局部最小值,使其训练精度不高,因此采用ABC算法优化BP神经网络,建立ABC-BP神经网络模型预测盾构地表沉降。

1.2 ABC算法

ABC算法[18]是一种模拟蜜蜂高效采集优质蜜源而形成的全局寻优求解的搜索算法,主要由引领蜂、跟随蜂、侦查蜂组成。寻优过程可分为3个阶段,引领蜂阶段、跟随蜂阶段、侦查蜂阶段。在三阶段开始前进行参数调整,主要包括种群数N、最大迭代次数M、局部最优解评判参数L1、搜索空间上限参数xj和下限参数nj、求解维度D等。一般定义种群数中的引领蜂数量和跟随蜂数量各占蜂群的一半且等于蜜源的数量,即一个引领蜂搜索采集一个蜜源。

1.2.1 引领蜂阶段

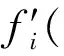
dij=nj+rand(0,1)(xj-nj)

(1)

(2)

(3)

式中fi为目标函数数值。

1.2.2 跟随蜂阶段

采用轮盘赌方式随机选取一个蜜源dij,然后用贪婪方式进行蜜源位置更新,若蜜源dij更新时采用式(4)进行,周围没有更优解,则记录蜜源停滞次数。

eij=dij+φ(dij-dkj) (k=1,2,…,N;k≠i)

(4)

式中:φ为取值在[-1,1]的随机数;dkj为邻域蜜源。

1.2.3 侦查蜂阶段

遍历种群看是否有蜜源dij停滞没有更新,即记录试验次数(T)大于等于L1,则该蜜源dij将被舍弃,此时侦查蜂采用式(5)随机产生一个新的蜜源dij,t+1位置替代,然后再重复引领蜂阶段,直到找到最优解。

(5)

引领蜂阶段、跟随蜂阶段、侦查蜂阶段3个阶段环环相扣,引领蜂用于维持优良解,跟随蜂用于提高收敛速度,侦查蜂用于增强摆脱局部最优的能力。算法计算过程中,需要记录最大迭代次数M,以及达到的允许误差。

2 工程实例验证

2.1 工程概况

南京地铁6号线十月广场站至金陵石化站,全长4007.821m,全线采用地下敷设方式。地铁隧道施工下穿地层主要包括中风化泥质砂岩、强风化安山岩、中风化安山岩和粉质黏土等,其中复合地层区段主要由中风化泥质砂岩与强风泥质砂岩复合,强风泥质砂岩与粉质黏土复合。根据纵断面勘察可知,盾构隧道施工主要可分为3种地层:中风化泥质砂岩,“上软下硬”地层,粉质黏土地层(图1)。

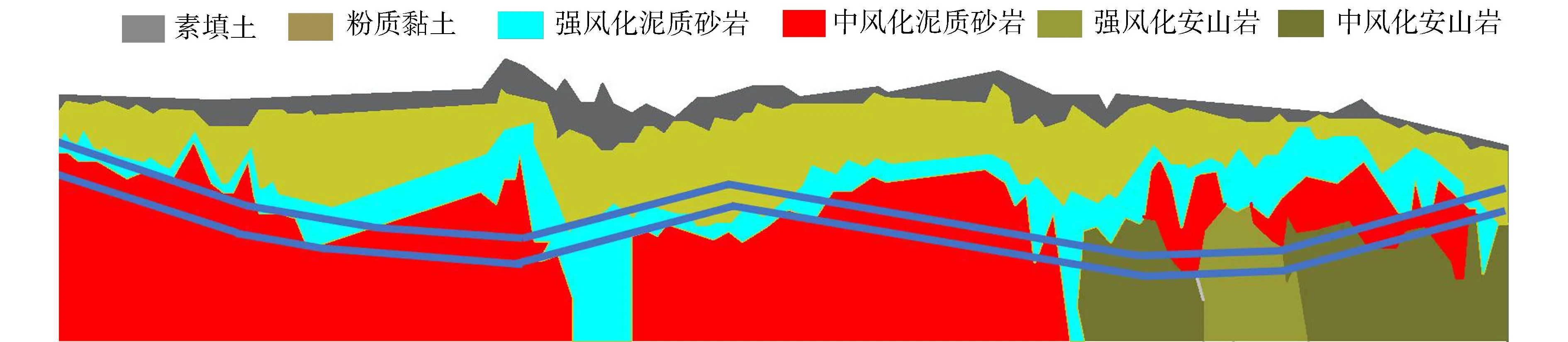
图1 工程纵断面

盾构施工采用铁建重工生产的土压平衡盾构机,盾构管片外径为6200mm,内径为5500mm,厚为350mm,环宽度为1200mm。盾构机主驱动为液压驱动方式,刀盘开口率为38%,转速可调范围0～3.44r/min ,标准扭矩6841kN·m,脱困扭矩8684kN·m,最大推力42575kN。

2.2 监测方案

由南京地铁6号线盾构区间工程实测资料及监测方案可知,盾构始发与接收端50环内地表沉降监测断面布设间距为5m,50～100环内地表沉降监测断面间距为20m,100环外布设间距为40m(图2)。当盾构机掘进至开挖面距离监测点50环时,断面监测开始记录;盾构机掘进至过监测点60环停止记录。即断面监测点从盾构开挖面前方50环内开始监测至盾构穿过断面,断面至盾构开挖面后方60环内监测完成,为断面监测全周期。

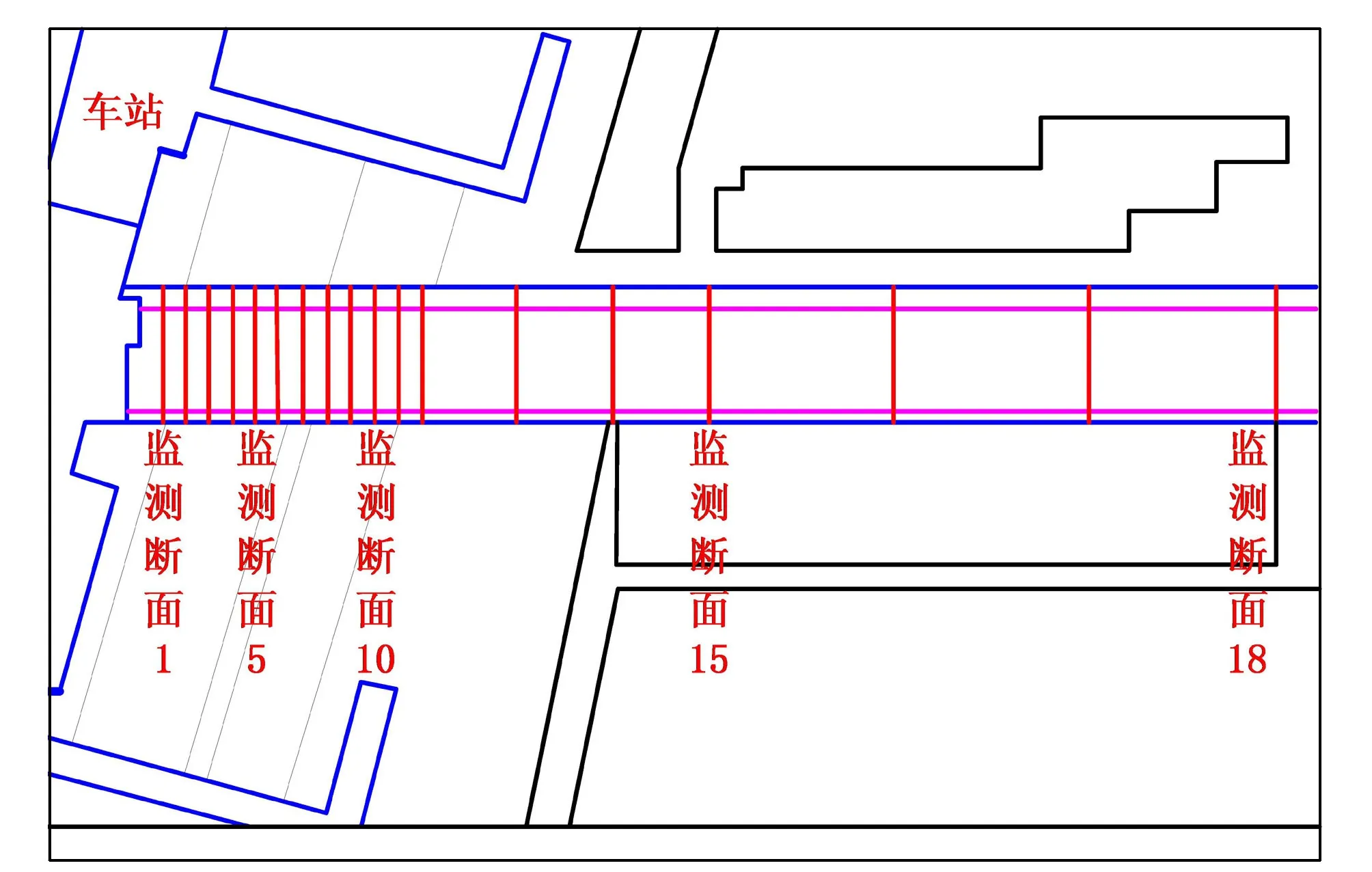
图2 盾构断面布置

为保证监测断面地表沉降点监测的连续性,基于现场施工监测方案,选取图2监测断面15～18区间的沉降点DB78-08、DB79-08、DB80-08、DB81-08、DB82-08的监测数据进行整理,完整选取以上断面全周期地表沉降监测日报数据,用于神经网络训练学习预测分析。其中,断面78沉降点DB78-08共有33组数据,断面79沉降点DB79-08共有30组,断面80沉降点DB80-08共有26组,断面81沉降点DB81-08共有28组,断面82沉降点DB82-08共有25组,断面地表沉降点为累计沉降值。

2.3 ABC-BP神经网络参数确定

a.输入参数与输出参数。地表沉降影响因素主要考虑地层参数与盾构掘进参数。地层参数包括土层压缩模量、黏聚力、内摩擦角、土层厚度、天然容重等5个参数。掘进参数主要考虑刀盘扭矩、总推力、土仓压力、同步注浆量等4个参数。在掘进过程中,监测断面与盾构开挖面的距离L不断变化,因此L也是地表沉降影响因素之一。因此,输入参数共有10个参数,输出参数为地表沉降。

b.隐含层节点数。隐含层节点数会直接影响神经网络的预测精度,根据研究[19],一层隐含层足以表达网络精度,单层隐含层节点数根据经验公式确定。

c.人工蜂群算法参数。ABC算法最优参数:蜂群大小为200,引领蜂和跟随蜂数量各为100,最大迭代次数为300,求解维度D=253,搜索空间范围nj=-10、xj=10,单个蜜源最大开采次数为5。BP神经网络最优参数:最大迭代次数为700,学习率为0.01,迭代精度为10-3。

对未掘进段断面地表沉降进行预测后,需与现场实测数据进行对比分析,并采用相关系数R和均方根误差RMSE评价模型的泛化能力。

2.4 地表沉降预测

选取沉降点DB78-08、DB79-08、DB80-08、DB81-08、DB82-08的监测数据进行模型验证。通过对多断面的地表沉降进行分析发现,受掘进参数和地层条件影响,相邻断面地表沉降趋势基本一致,因此用与预测断面前相邻两断面作为训练集,预测结果更具有代表性,即预测断面80时,用断面78和79的数据进行训练学习。按照同样方法,对断面81和断面82进行预测,验证对比ABC-BP神经网络与BP神经网络预测精度。

由于断面78、79、80的监测数据有部分为同一时间监测,若将数据按监测时间排列,会使数据点的位置重复,造成数据杂乱,不能直观地发现数据规律。借鉴钟国强等[20]数据处理的方法:首先对断面78监测全过程按时间顺序进行排序,再将断面79监测全过程按时间进行排序,选取样本为断面监测周期中测点开挖面位于测点前至盾构掘进到开挖面位于测点后这一过程中,开挖面地层参数、该环掘进参数与测点处累计沉降所构成的数据集。纵坐标为累计地表沉降累计值,横坐标为样本序号。

2.4.1 断面80地表沉降预测

断面80施工前,用沉降点DB78-08、DB79-08的地表沉降监测数据训练ABC-BP神经网络模型,然后预测盾构掘进时DB80-08的地表沉降。盾构时,产生新的数据,导入模型进行补充完善,再进行训练预测,并根据ABC-BP神经网络模型预测值及时调整现场施工参数,优化施工方案,进行信息化施工,有效指导施工。

由图3(图3～9中横轴为该监测断面开始监测至结束所记录的样本序号)可知,ABC-BP神经网络模型拟合效果更佳,BP神经网络模型会产生跳跃点,表明BP神经网络训练拟合具有不稳定性。ABC-BP神经网络模型训练结果:R=0.996,RMSE=4.052mm;BP网络模型训练结果:R=0.956,RMSE=7.834mm。整体而言,在训练集上,ABC-BP神经网络模型对断面78、79拟合效果优于BP神经网络模型。

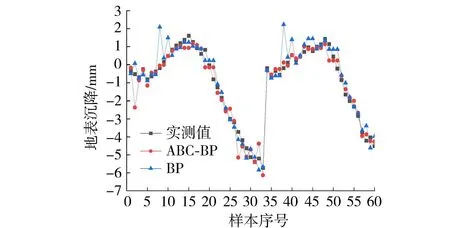
图3 DB78-08、DB79-08地表沉降训练结果

由图4可知,断面80地表沉降预测值大部分与实测值接近,最大误差不超过1mm。ABC-BP神经网络模型的预测结果RMSE=2.1738mm,R=0.988,BP神经网络模型的预测结果RMSE=3.0364mm,R=0.972,ABC-BP神经网络的预测效果优于BP神经网络,也证明了ABC算法提高了神经网络预测精度。

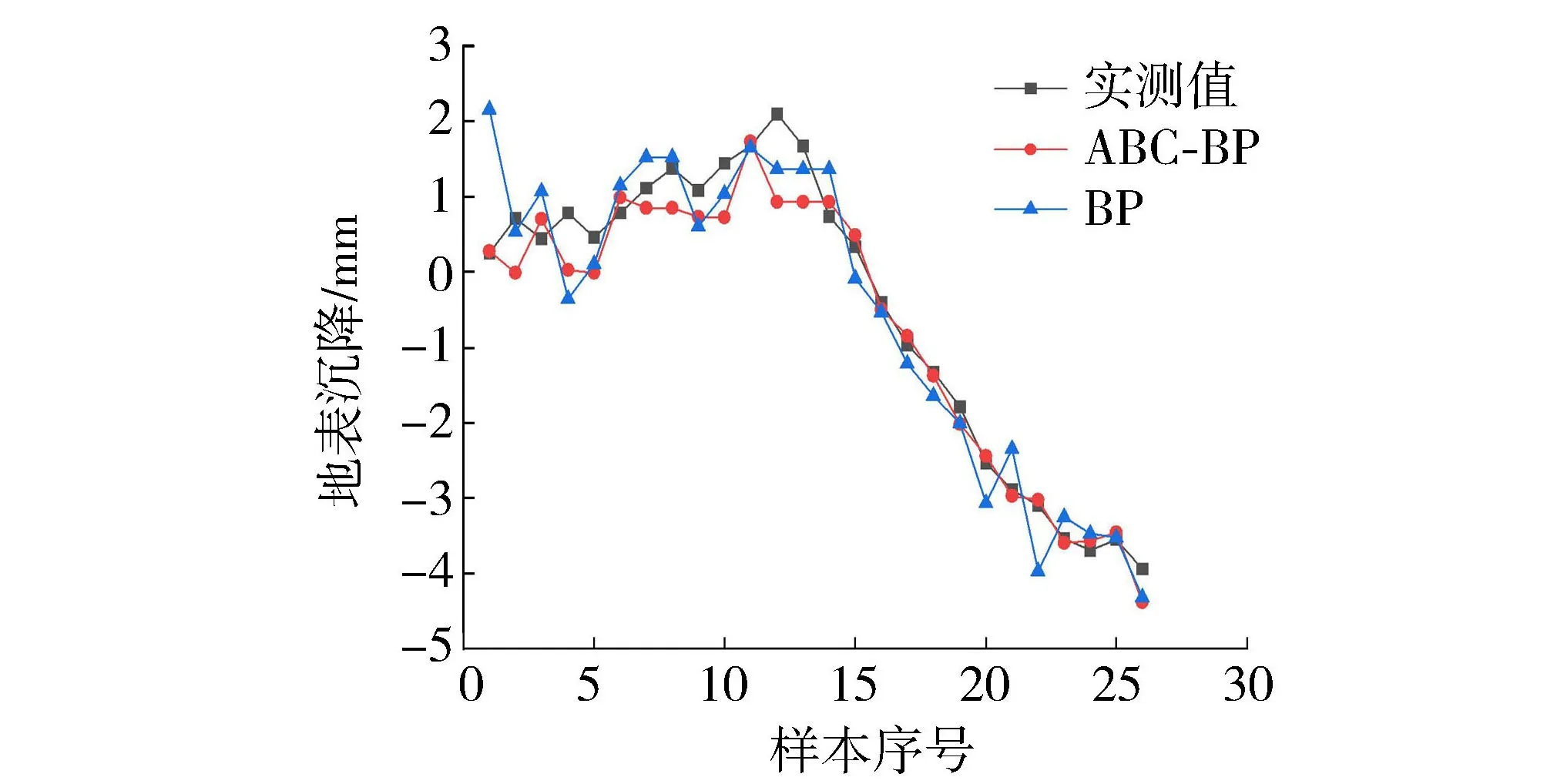
图4 DB80-08地表沉降预测结果

2.4.2 断面81地表沉降预测

收集断面79、80地表沉降监测数据,重新对ABC-BP神经网络进行训练学习,同时,盾构产生的新数据,不断导入模型训练,及时更新ABC-BP神经网络,可有效保证模型预测精度。由图5可知,ABC-BP神经网络模型训练结果为R=0.992,RMSE=5.231mm,BP神经网络模型训练结果为R=0.979,RMSE=6.654mm,在训练集上,ABC-BP神经网络的拟合效果优于BP神经网络。

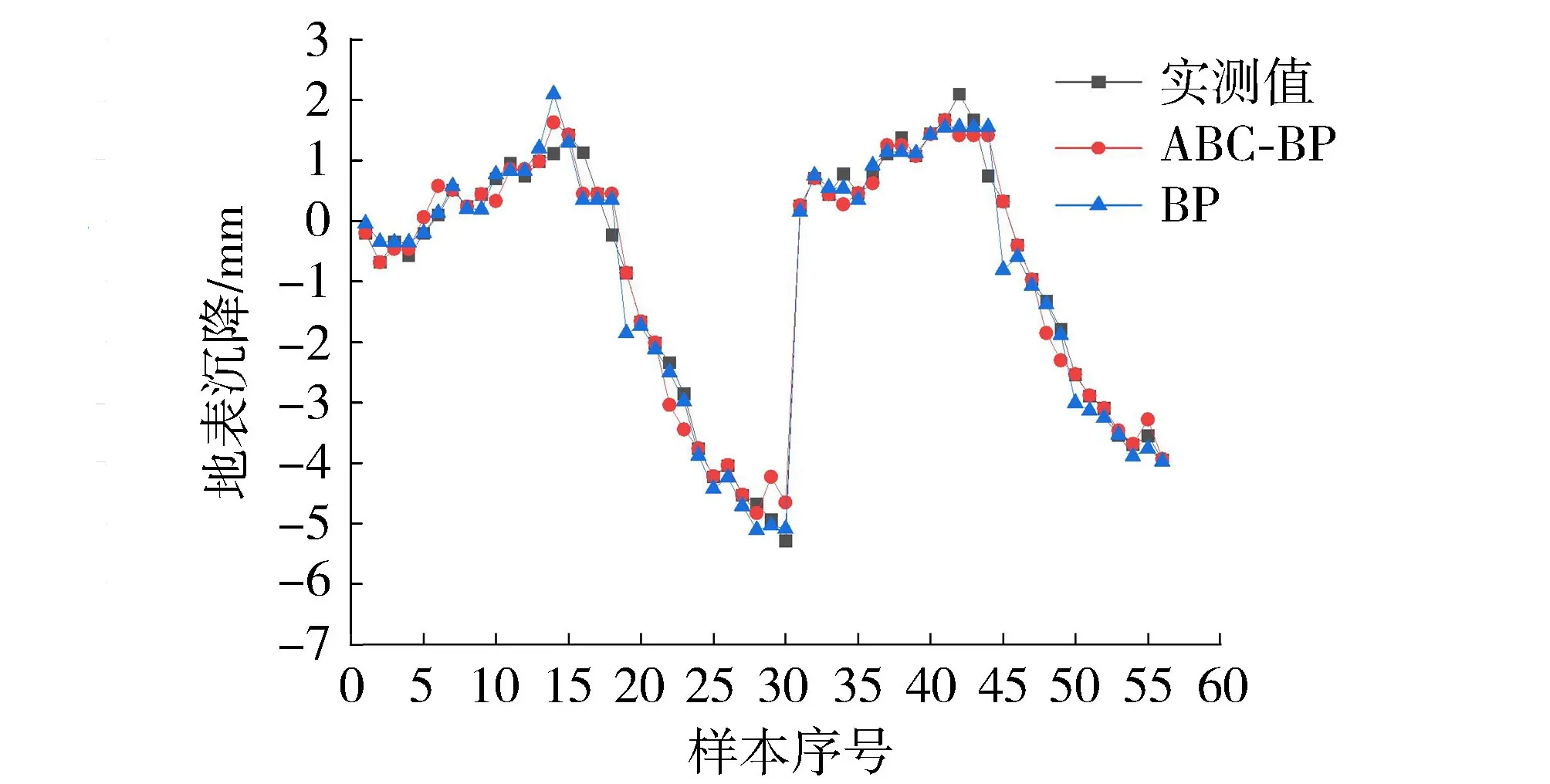
图5 DB79-08、DB80-08地表沉降训练结果

由图6可知,断面81地表沉降预测趋势与现场实测趋势基本一致,反映了神经网络具有很好的跟踪精度,较为完整地还原了现场实测数据的变化规律,预测值与真实值最大误差不超过1.5mm。ABC-BP神经网络模型的预测结果R=0.988,RMSE=4.635mm,BP神经网络模型的预测结果R=0.975,RMSE=5.962mm,ABC-BP预测效果也优于BP神经网络。

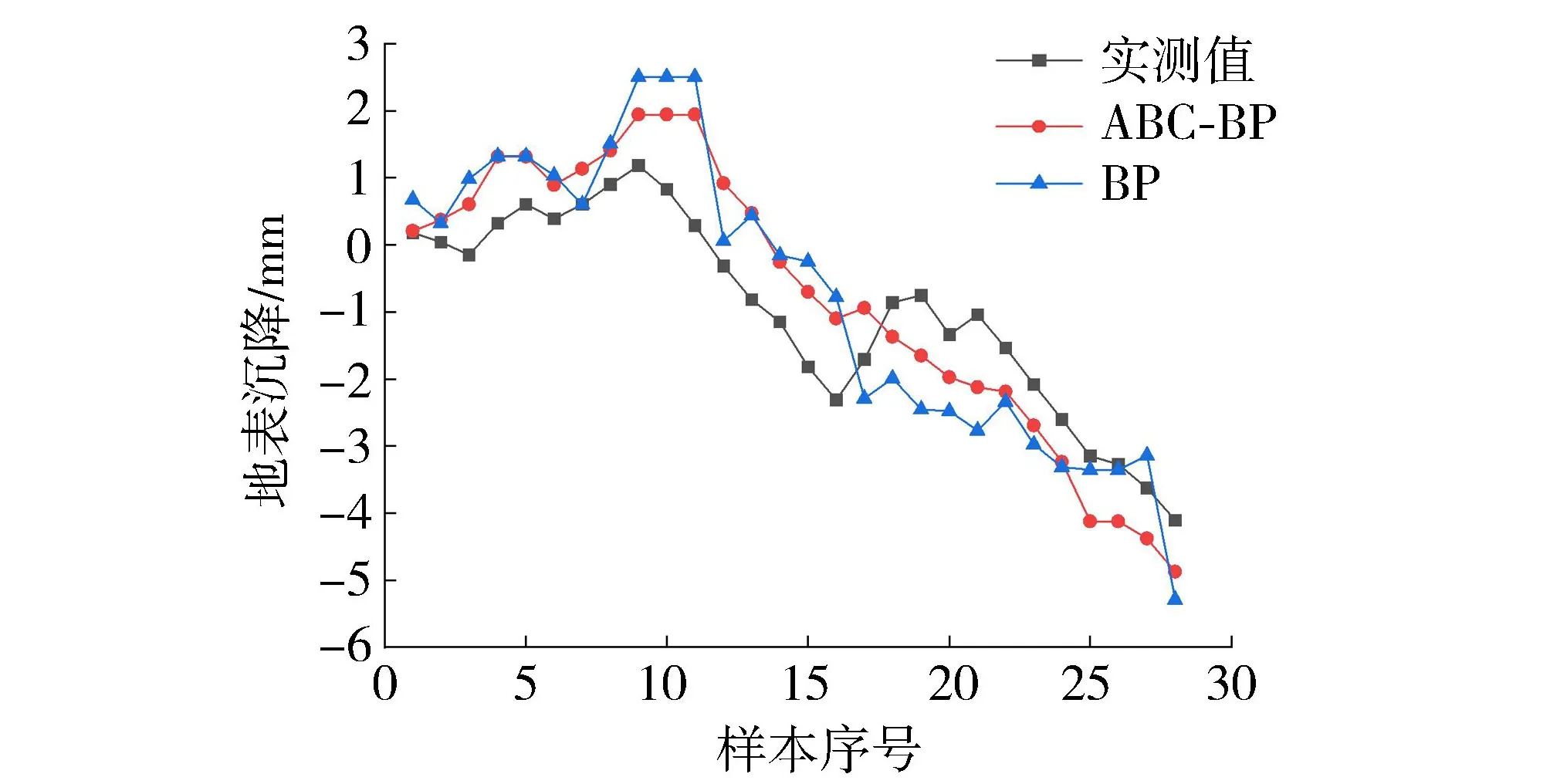
图6 DB81-08地表沉降预测结果

2.4.3 断面82地表沉降预测

收集断面80、81地表沉降监测数据,重新训练ABC-BP神经网络模型,预测断面82地表沉降。由图7可知,ABC-BP模型训练结果R=0.994,RMSE=5.034mm,BP模型训练结果R=0.945mm,RMSE=8.752mm,在训练集上,ABC-BP神经网络模型的拟合效果优于BP神经网络模型。

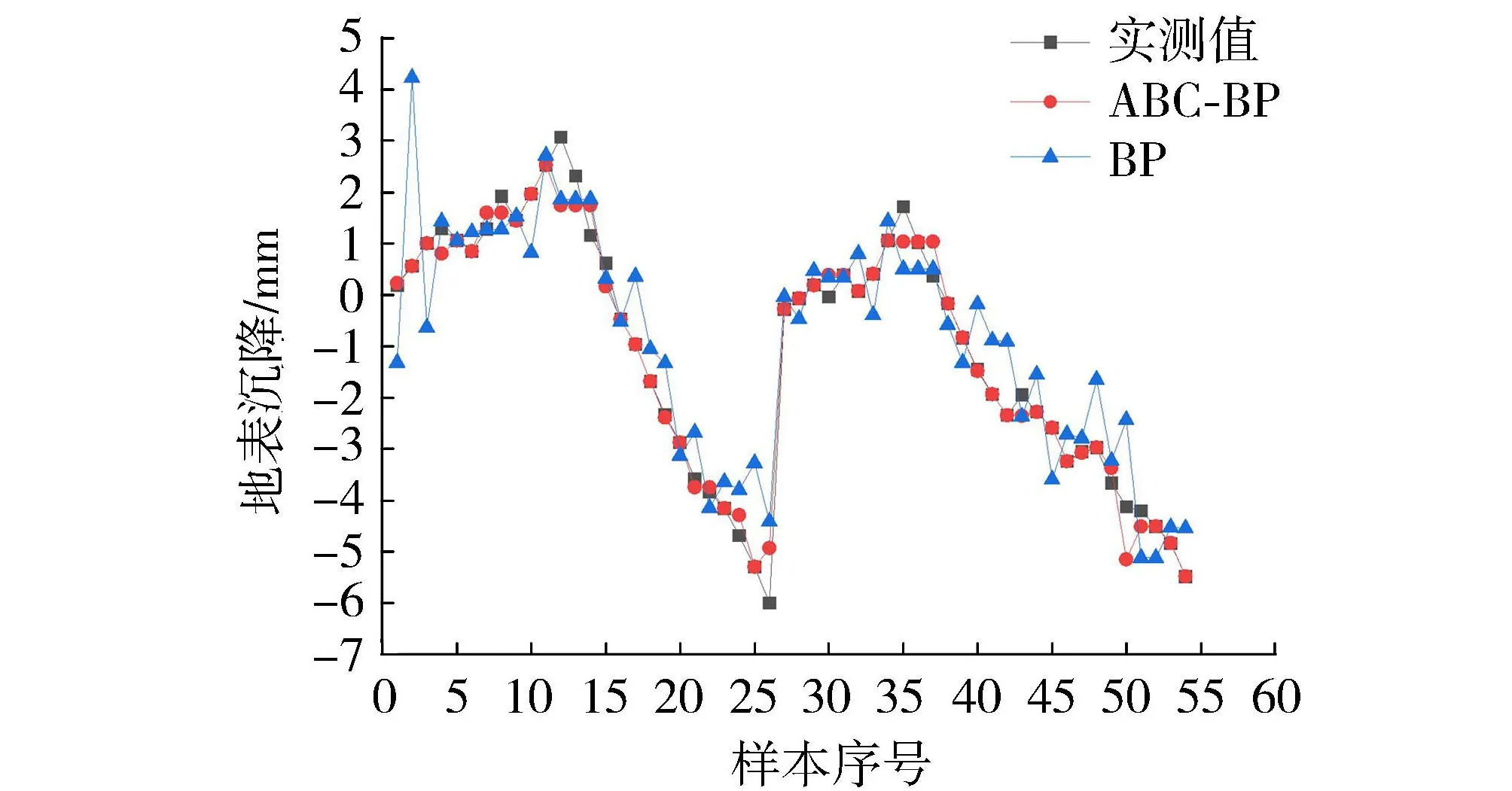
图7 DB80-08、DB81-08地表沉降训练结果

由图8可知,ABC-BP神经网络模型能够很好地拟合断面82地表沉降预测值,与实测值最大误差不超过1.5mm。同时,ABC-BP神经网络模型的预测结果为R=0.976,RMSE=4.636mm,而BP神经网络模型的预测结果为R=0.942,RMSE=7.062mm,因此,ABC-BP神经网络模型的预测效果优于BP神经网络模型。

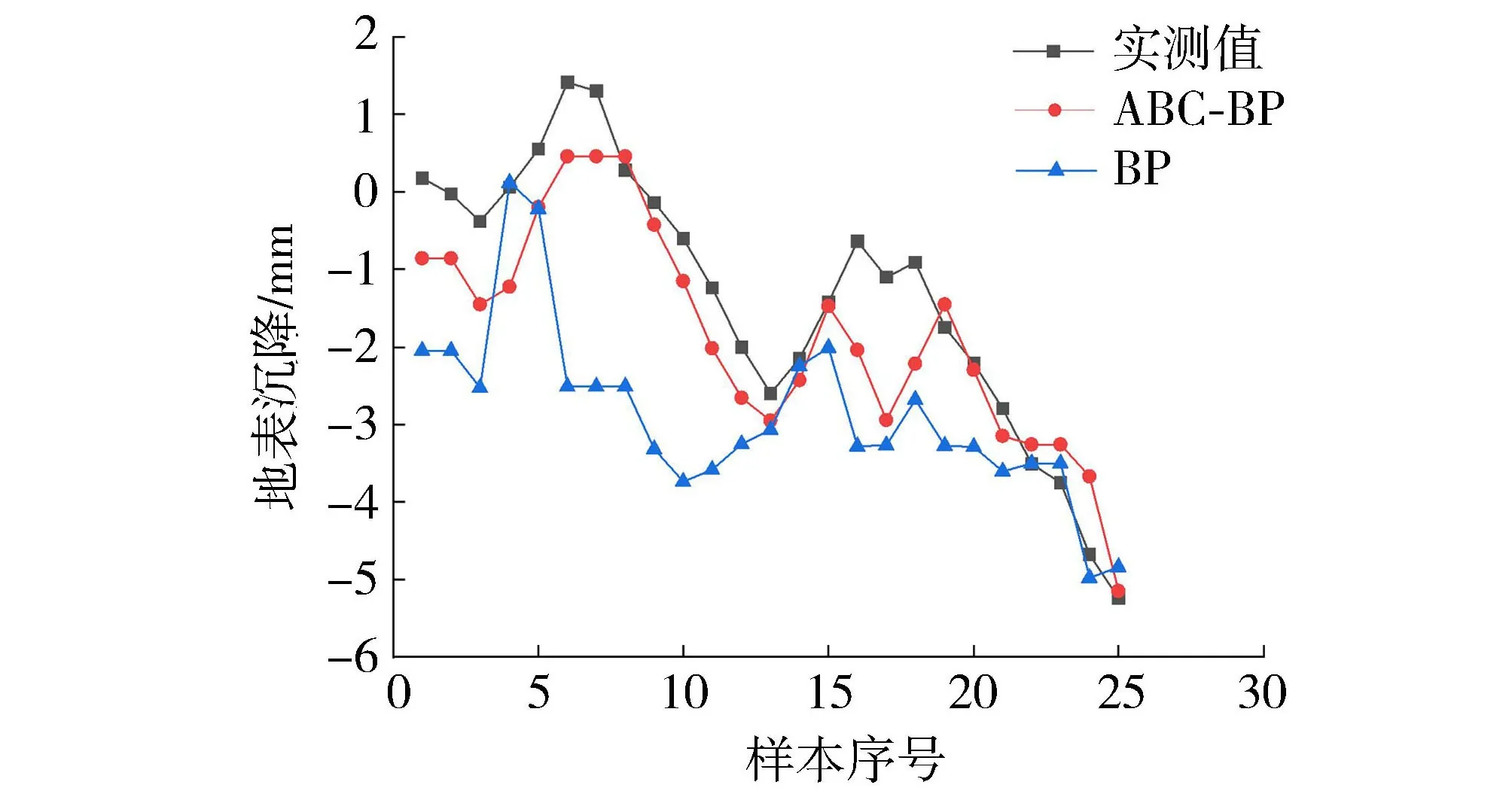
图8 DB82-08地表沉降预测结果

综上,ABC-BP神经网络模型的预测效果明显优于BP神经网络模型。单个断面进行预测时,ABC-BP神经网络模型与BP神经网络模型相比优势不明显;但对于连续断面进行预测时,断面82的BP神经网络模型预测开始偏离现场实测值,预测趋势与实测值偏离较大,存在不稳定性,可能会对现场施工带来安全隐患。ABC-BP神经网络模型对连续断面的预测稳定性提高,预测精度提高,预测收敛速度提高,其预测性能远远高于BP模型。

3 L对地表沉降S的影响

地表沉降是动态过程[21],是测点前后一定范围内掘进参数与地层参数相互作用的结果,采用盾构开挖面到监测断面的距离L描述盾构动态施工对测点地表沉降影响,不同的L对地表沉降S产生不同影响,以下分析L与S的关联性。断面78～82的L与S关系如图9所示。

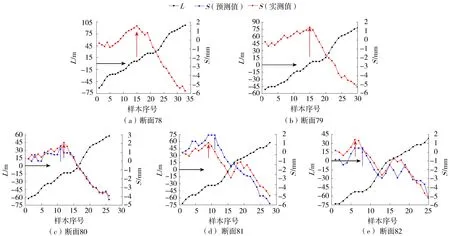
图9 断面78～82的L与S关系

由图9(a)可知,地表变形(累计值)先隆起后沉降,断面78地表沉降隆起峰值在L=0m处,符合现场施工规律,断面78前3环表现形式为沉降,第4环表现为隆起,表明盾构前4环掘进参数匹配不合理,造成地表变形先沉降后隆起变化。同理,第19环产生隆起,表明施工中存在掘进参数匹配相对不合理情况,导致地表沉降发生突变,对施工周边建筑造成安全隐患。

由图9(b)可知,断面79地表沉降隆起峰值在L=0m处,符合现场施工规律,断面79地表沉降存在较多跳跃点,沉降后隆起,表明该断面掘进参数匹配相对不合理,可综合分析不同掘进参数对地表沉降影响,制定相应的优化方案。

由图9(c)(d)(e)可知,断面80、81、82地表沉降趋势基本一致,先隆起后沉降,但地表隆起峰值相对L=0m处左移,提前达到隆起峰值。进一步说明断面80、81、82掘进参数匹配相对不合理,其中断面82后期又产生隆起,并不符合现场规律,各断面匹配的掘进参数并不是最优,要使地表沉降达到最小,需进行掘进参数优化。

断面78～82与盾构地表沉降关联性分析可知,地表变形(累计值)先隆起后沉降,L近似直线分布,可以认为盾构开挖过程近似匀速前进,有利于减小地表沉降。分析L可作为直观判断掘进参数是否最优的辅助手段,也进一步说明合理匹配掘进参数对地表沉降控制而言至关重要。

4 讨 论

第2.4节证明了ABC-BP神经网络模型预测精度优于BP神经网络模型,同时可通过地层参数和掘进参数预测相应的地表沉降。

如何采用ABC-BP神经网络预测地表沉降并指导现场施工,是需要解决的问题。要实现现场施工应用,需再构建盾构掘进参数预测模型(简称“模型A”),即构建地层参数与掘进参数非线性关系,通过地层条件预测相应的掘进参数。而评价掘进参数预测是否合理,需要以地表沉降为评价指标,需通过ABC-BP神经网络地表沉降预测模型(简称“模型B”)实现,以模型A掘进参数预测值作为模型B的输入端,预测该掘进参数条件下对应的地表沉降变化值,进而实现掘进参数优化。

对于盾构后续段施工,需提前预测合理的掘进参数以及地表沉降,开展相关掘进参数优化方案研究。通过以上应用流程可得到不同的掘进参数下地表沉降取值范围,使之既可以判断该掘进参数施工下的地表沉降发生范围,还可根据地表沉降量进行盾构掘进参数优化,实现掘进参数与地表沉降关联性。基于ABC-BP神经网络模型现场施工应用流程如图10所示。

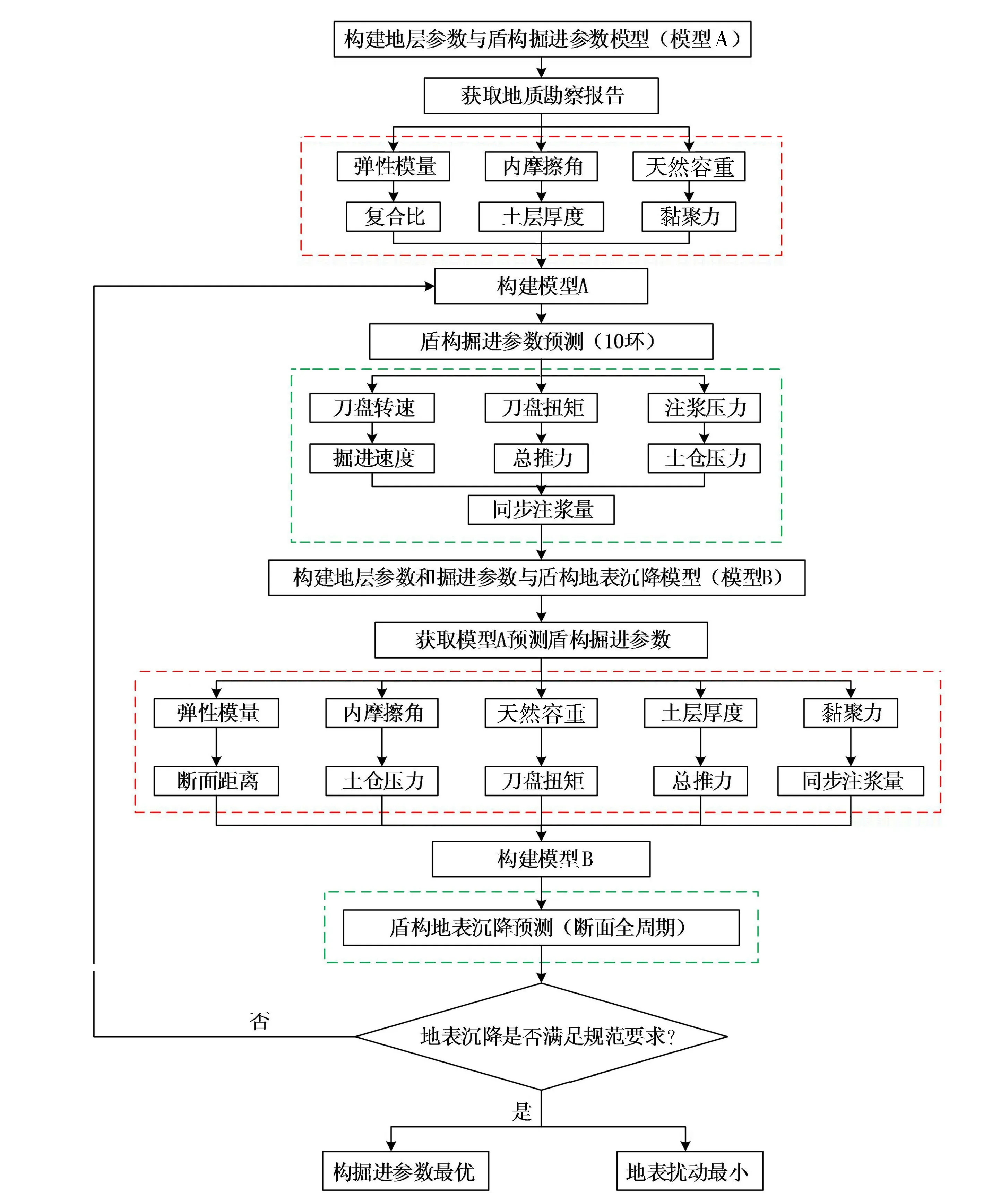
图10 ABC-BP神经网络现场施工应用流程

针对现场施工应用存在问题的解决方法:①对于无过往数据进行训练导致数据集匮乏的问题。ABC-BP神经网络模型现场前期应用可基于大数据平台类似数据分享,建立可具一定参考性的预测数据,同时数值模拟也可在项目前期进行预测,预测结果作为神经网络的训练集,对比分析预测结果,实现动态预测,以解决盾构施工前期训练数据不足问题。②模型A需要土层参数作为输入,在面对复合地层时,存在如何表征复合地层下土层参数的问题。基于神经网络现场应用思路中提出的模型A输入参数定义复合比概念,即盾构开挖面上下地层面积之比,地层输入参数根据复合比采用加权后弹性模量、内摩擦角、黏聚力等定义复合地层,使模型A具备复合地层条件预测功能。基于此,可加入更多参数定义完善神经网络预测模型在不同情景下预测准确性。

5 结 论

a.利用人工蜂群算法ABC优化BP神经网络,有效解决了BP神经网络训练过程中容易陷入局部最小值问题,同时,对连续3个断面地表沉降预测可知,ABC-BP神经网络模型稳定性有显著提高,预测效果优于BP神经网络模型,在一定程度上克服了BP随机初始化训练的缺点。

b.盾构开挖面到监测断面的距离L可以很好地反映盾构施工地表沉降动态变化过程,断面地表沉降变化趋势基本一致,先隆起后沉降,隆起峰值在L=0m处,可根据不同L处的地表沉降值直观判断掘进参数是否最优。

c.ABC-BP神经网络模型预测盾构地表沉降具备现场应用推广能力,符合现场施工要求,基于此,提出了适应于指导施工的神经网络预测模型应用流程,可用于地铁盾构地表沉降预测。