桩承载力反向自平衡试桩法数值模拟分析

刘永莉,刘志杰,巴军涛,肖衡林,郭 斌

(1.湖北工业大学土木建筑与环境学院,湖北 武汉 430068; 2.中交二航局建筑工程有限公司,湖北 武汉 430056)

桩基础因其承载力高、沉降小、适应性强、抗震性能好等优点,在各种高层建筑、桥梁和港口码头等工程领域中应用广泛[1]。目前,基桩承载力确定方法主要包括传统静载试桩法和自平衡试桩法[2]。传统静载试验法是检测基桩承载力最可靠的方法,但因受到施工场地和试桩吨位等因素限制,难以满足特殊场地和大吨位基桩承载力的测试[3-4]。自平衡试桩法利用桩的自重和侧摩阻力作为桩端阻力的反力,不需要在桩周设置反力架或进行重物堆载,突破了试桩吨位的限制,特别适用于施工场地受限的大吨位基桩试验[5-6]。自平衡试桩法因具有省时省力、试验方便、适应性强等优点,已在许多实际工程中得到应用[7-8],也相继出台了行业和部分省份的技术规程[9-11]。由于自平衡试桩法的荷载作用位置及传递方向不同于传统静载试桩法,在根据测试结果确定基桩承载力时需将负摩阻力转换为正摩阻力,最常用的方法是通过选取合适的转换系数进行换算[12],相关研究也给出了不同土层中的正、负摩阻力的转换系数建议值[13-16],但由于各土层的不均匀分布和桩土相互作用机制的复杂性,难以精确给出实际工况下的转换系数。

为克服自平衡试桩法正、负摩阻力转换导致基桩承载力测试结果不直观的问题,刘永莉等[17-19]提出了一种单桩竖向承载力反向自平衡试桩法,该方法在自平衡试验的基础上增加了一套桩顶竖向加载装置,与自平衡试桩法组合使用,可克服自平衡试桩法上段桩负摩阻力换算成正摩阻力时转换系数难以准确确定的问题,同时也可用于测试基桩的抗拉承载力。

目前,反向自平衡试桩法仅处于理论研究阶段,要将该方法应用到工程实践中还有很多问题亟待解决。现场原位试验是基桩研究中最可靠的方法,但需要耗费大量的人力、物力、财力和时间等;室内模型试验相对现场试验虽然可以降低试验费用,但模型试验由于是缩尺试验,如果试验参数设计不合理,试验结果往往与工程实际结果差别较大,且直接采用室内模型试验研究反向自平衡试桩法有一定的盲目性[20-21]。为此,本文采用ABAQUS有限元分析方法,通过建立反向自平衡试桩法数值模型,分别采用位移控制法和荷载控制法进行桩身和桩顶加载模拟,以探究反向自平衡试桩法的可行性,进而推动反向自平衡试桩法在实际工程中的应用。

1 反向自平衡试桩法测试步骤

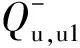
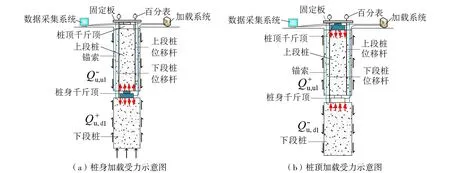
图1 反向自平衡试桩法加载受力情况

从测试技术上分析,反向自平衡试桩法充分继承了自平衡试桩法的优点,不需要额外的锚桩或堆载材料就可实现桩基承载力的检测;同时,相较于自平衡试桩法又避免了负摩阻力的转换问题,可直接通过荷载-位移曲线获取基桩抗压极限承载力,还可以得到对应桩的竖向极限抗拔力。

2 反向自平衡试桩的有限元模型

2.1 模型假设条件

为简化计算,在建立有限元模型时做如下假设:①桩体为均质理想弹性体,不考虑桩自身的弯曲变形;土体考虑为均质弹塑性材料,不考虑土的剪胀性;桩侧土体在桩长范围内为同一均质岩土层。②不考虑管桩土塞效应对承载力的影响。③桩与岩土之间的摩擦系数保持不变。④土体采用总应力分析方法分析,不考虑孔隙水压力影响和岩层倾斜。⑤不考虑加载顺序对测试结果的影响。

2.2 模型构建

在研究土与结构物相互作用时,由于三维有限元模型单元设置数量多,计算时间长,而平面二维应变土体模型因其简单实用的优点得到广泛运用,且其简化模型基本可以满足工程应用的精度要求[22]。本文考虑到桩-土结构及施加荷载均具有轴对称特点,采用以桩中心线为对称轴建立平面二维应变土体模型进行数值模拟分析。

数值模型的几何结构如图2所示,其中,上段桩桩长取8m,下段桩桩长取4m,桩径为1.6m,壁厚为10cm。考虑桩周土和桩端岩层的影响范围,土体宽度取20倍桩径,深度取2倍桩长[23-24],即模型计算土体宽度取32m,计算深度取24m。其中土体模型顶部为自由边无约束,底部采用固定约束,外侧为径向的位移约束;桩顶部自由无约束。在单元网格的划分上,靠近桩体的地方网格密、远离桩体的地方网格稀疏。桩和土体均采用节点四边形线性平面应变减缩积分单元,此单元类型对位移的求解结果较精确。

图2 数值模型的几何结构

桩体采用线弹性管桩模型,其弹性模量为40GPa,泊松比为0.16;桩端基岩采用Mohr-Coulomb本构模型,其弹性模量为1100MPa,泊松比为0.25,黏聚力为800kPa,内摩擦角为36°;填土为饱和黏性土,其不排水强度cu为24kPa,为了模拟不排水加载条件,采用总应力分析方法进行分析,不排水强度可以采用Mohr-Coulomb模型或者小应变刚度硬化土体模型(HSS)模拟[25],则其土体弹性模量为500cu,即12MPa,泊松比为0.495,黏聚力为24kPa,内摩擦角为0°。具体桩土参数如表1所示。

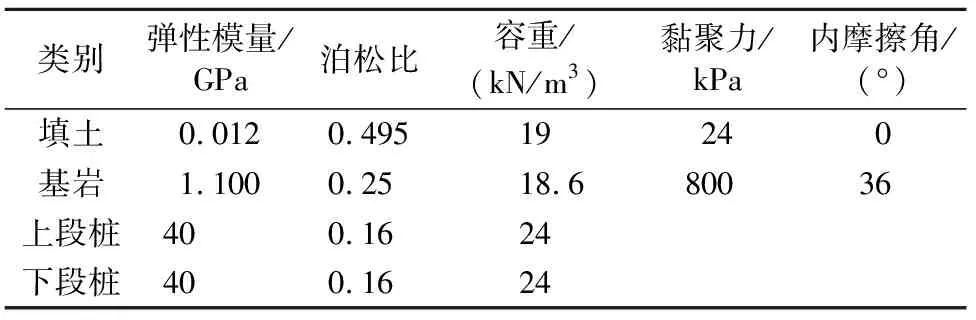
表1 桩土参数

2.3 桩土相互作用

桩土接触问题通过设置接触对和定义接触性质来模拟,本文从桩生效的分析步开始,采用面面接触对类型来模拟桩与外侧岩土、桩与桩底基岩之间的接触面,由于桩相对岩土的刚度大,取桩为主控面,岩土为从属面,桩与土体接触跟踪均采用有限滑移方法。桩与岩土接触面的接触性质包括两个方面,一是法向采用“硬接触”且允许分离,二是切向采用库伦罚刚度算法来确定摩擦系数[26]。

2.4 初始地应力平衡与加载步骤

由于在桩浇筑之前,土体自重产生的变形就已经完成,因此对创建的数值模型先进行地应力平衡。在ABAQUS软件中,常见的地应力平衡方法有3种:自动地应力平衡法、关键字定义初始地应力法和开源数据库(open data base)导入法[27]。由于自动地应力平衡法相对更容易操作,故本文采用ABAQUS提供的自动地应力平衡法功能对土体进行初始地应力平衡。由于创建的数值模型是用于桩土相互作用分析的,则在地应力分析中土体不能有桩土接触对和桩单元。具体加载步骤为:

步骤1采用生死单元法“杀死”桩单元以及桩土接触对,并约束土体的水平位移,再施加土体重力,进行自动地应力平衡。

步骤2完成地应力平衡后,激活桩单元以及桩土接触对,取消桩孔的水平约束,施加桩重力。

步骤3当桩身加载时,钝化桩顶进行加载分析。

步骤4当桩顶加载时,钝化桩身进行加载分析。

2.5 加载方法与过程

ABAQUS软件可提供两种荷载施加方法,一是荷载直接作用在桩顶,二是通过对桩顶施加位移,达到对桩施加荷载的目的。前者通过记录各级荷载下桩身的位移,得到最终的荷载-位移曲线;后者通过施加位移得到桩所受的对应荷载,进而得到荷载-位移曲线。由于反向自平衡试验的平衡点难以精确确定,直接采用荷载控制法较为烦琐,为了使上、下段桩承载力均能达到极限状态,便于与传统静载试验进行极限承载力比较,本文首先采用位移控制法模拟上、下段桩的加载,得到上、下桩的极限承载力,然后根据得到的极限承载力,通过荷载控制法分级施加荷载,以模拟上、下段桩同时等量加载过程。

加载过程中,上、下段桩作为两个单元分别建模,两桩之间接触部位无相互作用。先在两桩之间接触部位分别施加上段桩桩底向上位移荷载和下段桩桩顶向下位移荷载,以模拟桩身加载;然后通过施加上段桩桩顶向下位移荷载和下段桩桩顶向上位移荷载,以模拟桩顶加载。

3 模拟结果与分析

3.1 位移控制法的荷载-位移曲线

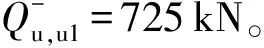
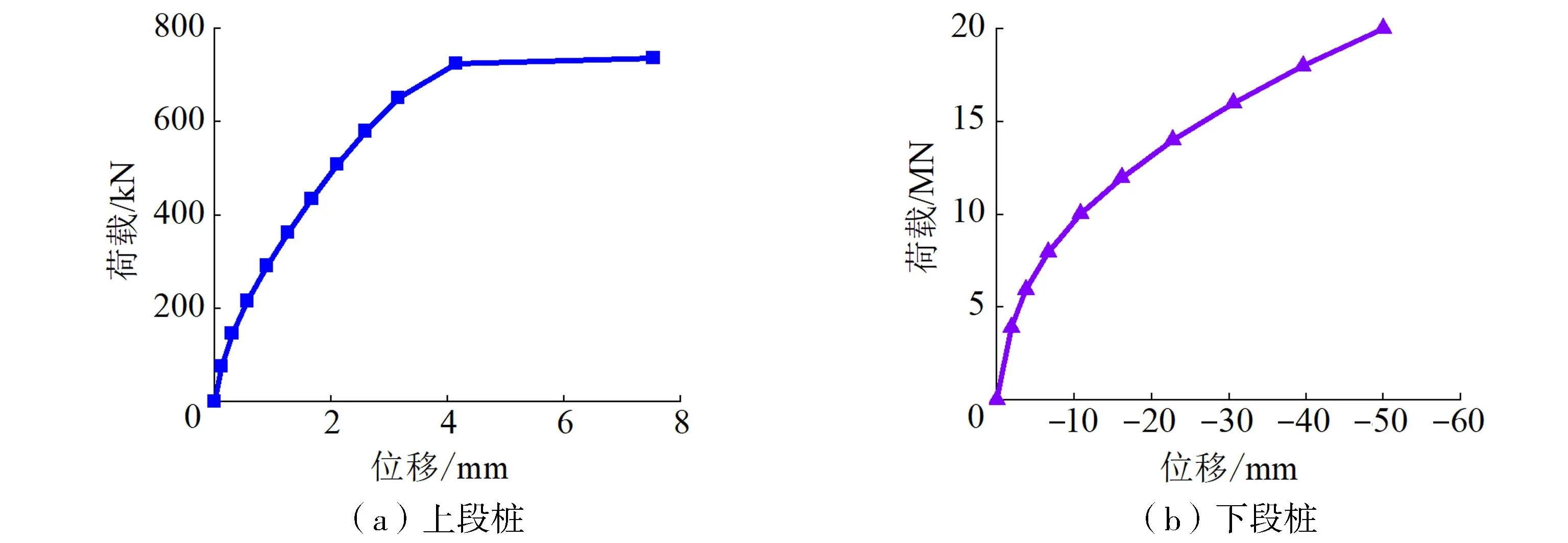
图3 位移控制法下桩身加载时的荷载-位移曲线

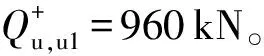
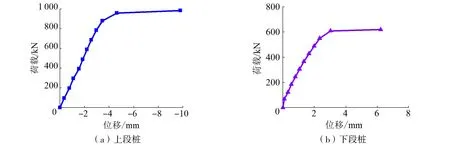
图4 位移控制法下桩顶加载时的荷载-位移曲线

图5为传统静载试验时,采用位移控制法得到的静压桩荷载-位移曲线,桩顶荷载随着桩顶沉降增大而逐渐增大,整个曲线未出现明显突变点,为缓变型曲线,其桩体竖向承载力极限值取最终施加位移对应的荷载,即Qua=21235kN。

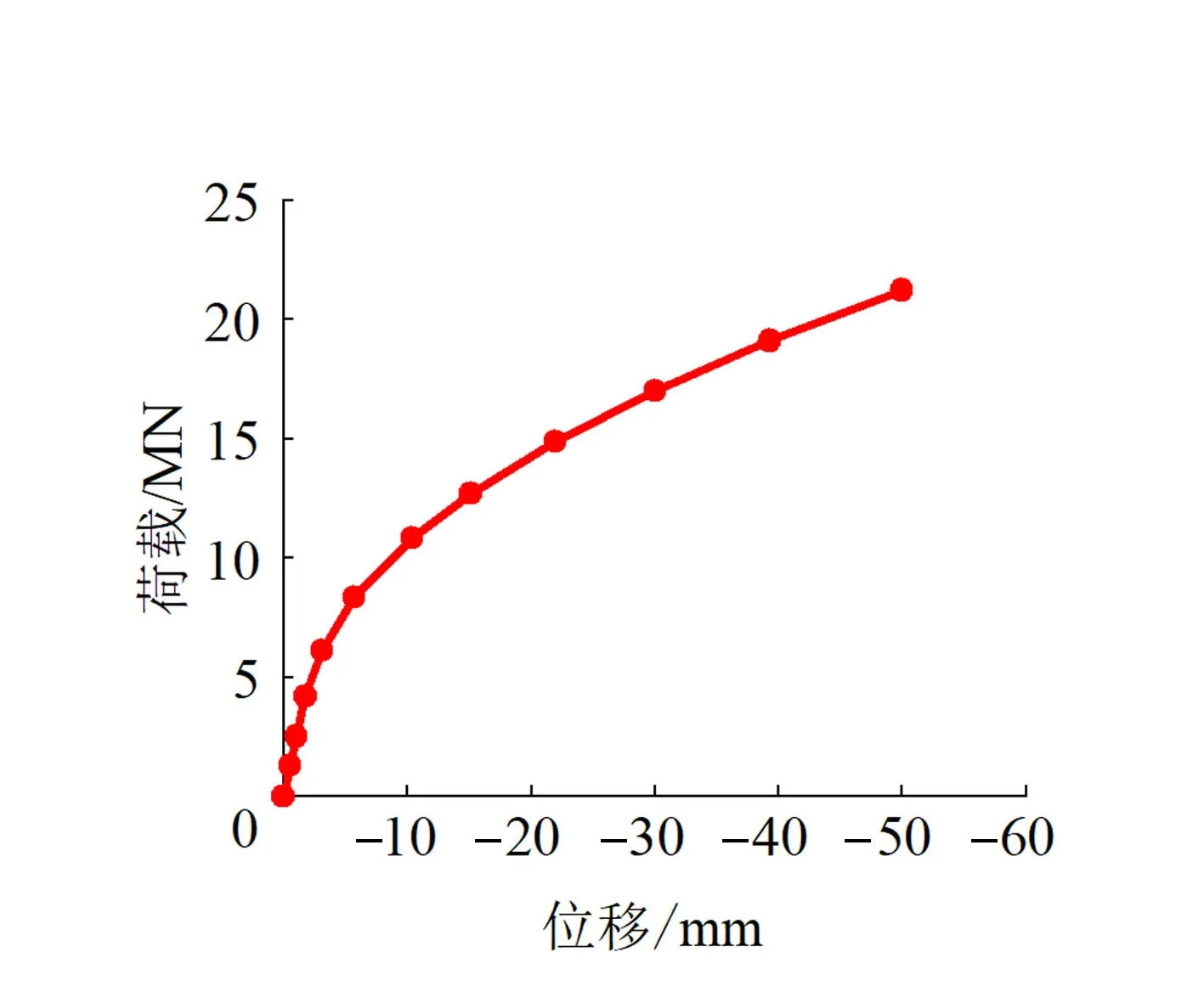
图5 静压桩的荷载-位移曲线

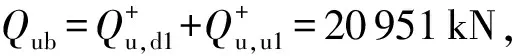
3.2 荷载控制法的荷载-位移曲线

图6为反向自平衡试验不同加载方式下,采用荷载控制法得到的上、下段桩荷载-位移曲线。在桩身加载时,上段桩变化曲线与采用位移控制法的变化曲线一致,而下段桩在荷载达到725kN之前曲线呈现线性增长,说明下段桩的承载力还远未达到极限值,可判断桩身加载时,其加载位置相较于桩体真实平衡点位置偏上。在桩顶加载时,下段桩变化曲线与采用位移控制法的变化曲线一致,在Q=610kN处,曲线出现明显陡降点,此时上段桩承载力并未达到极限,可判断桩顶加载时,桩顶平衡点相较于真实平衡点位置偏下。

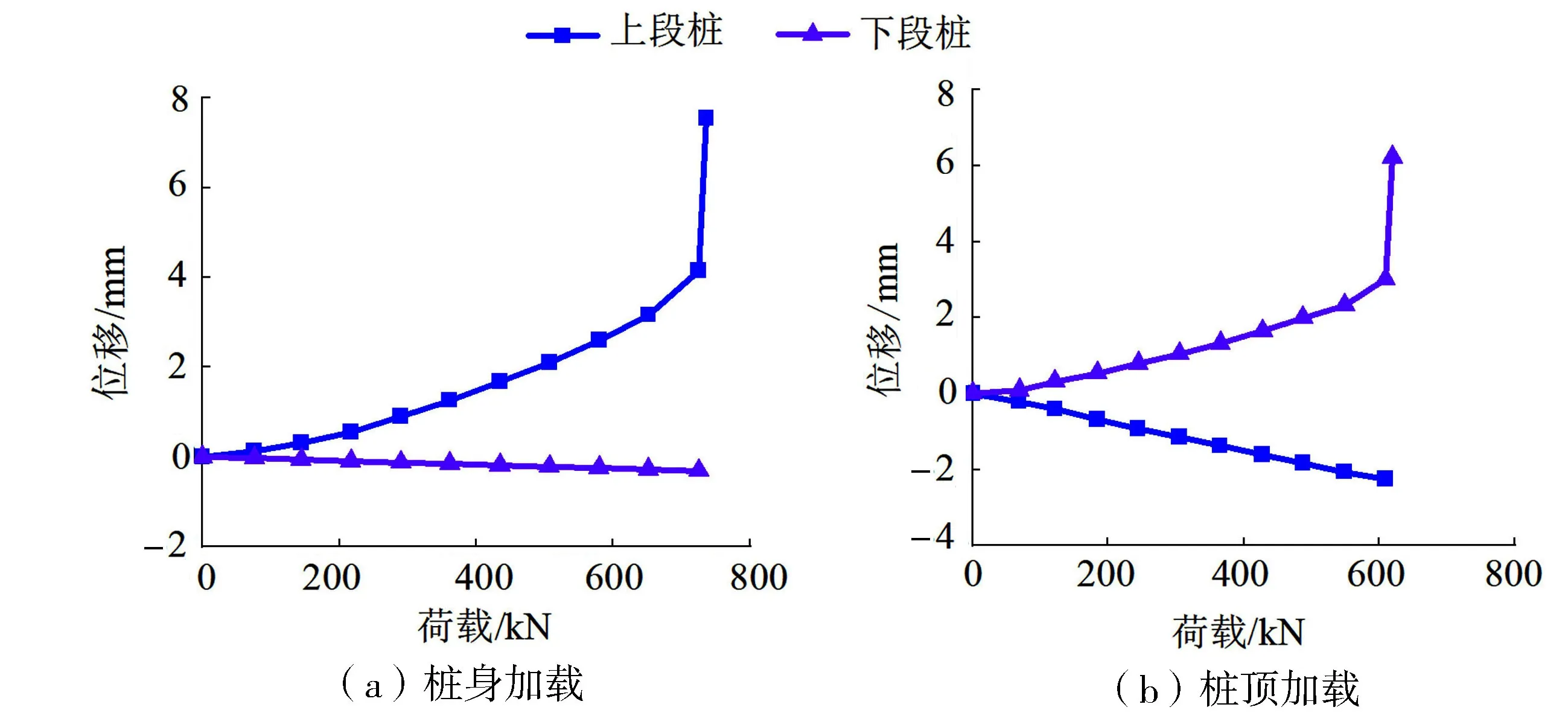
图6 荷载控制法下桩体的荷载-位移曲线

因此,反向自平衡试桩法与自平衡试桩法一样,均存在平衡点难以精确确定的问题。对于反向自平衡试桩法,由于分桩身和桩顶两次加载,要确定两次平衡点。若不考虑桩体自重,第一次桩身加载时上段桩负摩阻力与下段桩正摩阻力及桩端阻力相平衡,第二次桩顶加载时上段桩正摩阻力与下段桩负摩阻力相平衡。若为摩擦桩或桩端阻力占比较小的情况时,平衡点位置的判断则主要由上、下段桩侧摩阻力所决定。

3.3 轴力分析

图7为反向自平衡试验不同加载方式下,桩身轴力随深度变化的曲线。荷载遵循从加载端向远离端传递的规律。由图7(a)可知,桩身加载时,荷载分别作用于上段桩桩底和下段桩桩顶,上段桩受到向上支撑作用,荷载自下而上传递,同一荷载下,离平衡点位置越近,轴力越大,并向桩顶方向逐渐衰减,轴力曲线整体向“下”侧凸起,且凸起程度随着荷载增大而趋于平缓,说明上段桩顶部随荷载增大开始逐渐受到侧摩阻力的作用。下段桩受到向下顶压作用,荷载自上而下传递,当荷载较小时,桩顶荷载和桩端荷载差别较小,此时桩所受侧摩阻力很小,随着荷载增大,桩端阻力增长显著,荷载主要由桩端阻力承担。由图7(b)可知,桩顶加载时上段桩类似于纯摩擦桩,下段桩为抗拔桩。上、下段桩的轴力传递规律相同,都是自上而下进行传递,荷载全部由侧摩阻力承担,随着荷载的逐渐增大,下段桩桩周土层逐渐激发侧摩阻力,且下部土层轴力衰减逐渐增大,轴力变化主要集中在桩的上部。

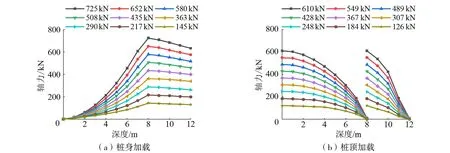
图7 桩身轴力随深度变化曲线

3.4 侧摩阻力分析

图8为反向自平衡试验不同加载方式下,桩身侧摩阻力随深度变化的曲线。由图8(a)可知,桩身加载时,上段桩侧摩阻力随荷载增大而增大,且沿桩向下逐渐递增,侧摩阻力呈下大上小的分布形式,说明桩周的下部土层先于上部土层发挥侧摩阻力的作用。由图8(b)可知,桩顶加载时,上段桩侧摩阻力也沿桩向下逐渐递增,桩的最大侧摩阻力发生在桩底位置,随着荷载逐渐增大,桩侧摩阻力增加的幅度也逐渐增大。由图8(c)可知,桩顶加载时,下段桩侧摩阻力也沿桩向下逐渐递增,侧摩阻力呈下大上小的分布形式。

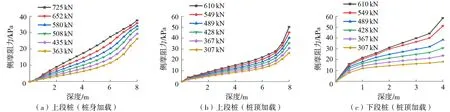
图8 桩侧摩阻力随深度的变化曲线

4 结 论

a.反向自平衡试桩法可以克服自平衡试桩法正、负摩阻力转换的问题,相对于自平衡试桩法,其测试结果更为直观。

b.反向自平衡试验结果与静载试验结果较为一致,反向自平衡试桩法用于测试基桩承载力具有可行性。

c.反向自平衡试桩法和自平衡试桩法均存在平衡点位置确定的问题,对于反向自平衡试桩法,由于分为桩身和桩顶两次加载,导致其加载中需要确定两次平衡点位置。在不考虑桩体自重的情况下,第一次桩身加载时上段桩负摩阻力与下段桩正摩阻力及桩端阻力相平衡,第二次桩顶加载时上段桩正摩阻力与下段桩负摩阻力相平衡。若为摩擦桩或桩端阻力占比较小的情况时,平衡点位置的判断主要由上、下段桩侧摩阻力所决定。