静压沉桩后黏土中超孔压时空分布规律研究

张智慧,朱文文,马 天,刘 坚,刘洋义

(辽宁工程技术大学力学与工程学院,辽宁 阜新 123000)

天然含水量大、压缩性高和承载力低的黏土层在荷载作用下的变形会逐渐增大,沉降时间不断延长[1-2],可采用质量可靠、造价相对较低和施工速度快的预应力高强度混凝土(pre-stressed high-strength concrete,PHC)管桩提高地基承载力[3-5]。在饱和软黏土中打入或压入PHC管桩,土体中会产生应力场和较高的超孔隙水压力(以下简称为“超孔压”)等[6-7],从沉桩开始伴随着超孔压的产生、消散或固结,某一时刻土体的有效应力可能会出现负值,影响管桩基础的承载力。在海洋桩基工程中,海床土体内孔压及有效应力在时空上的不均匀变化可能使土骨架产生液化或剪切破坏,通过影响桩基承载特性从而使海工结构物失稳[8]。因此,仍需对静压沉桩引起的超孔压和有效应力的变化规律进行研究。

国内外学者主要通过理论分析、试验研究和数值模拟等方法对沉桩引起的孔隙水压力(以下简称“孔压”,为静孔压和超静孔压之和)分布和土体应力场进行定量分析[9]。在理论分析方面,Poulos等[10]应用小孔扩张理论分析了PHC管桩周围土体中超孔压的分布;路德春等[11]依据土体和荷载两个条件,分析和明确了有效应力原理及其物理定义,揭示了孔压对土体物理力学特性的影响机理;唐晓武等[12]改进了时变荷载下地基的径向和竖向两个方向的组合孔压解析解,发现开孔PHC管桩具有最好的孔压消散能力;Mousavi等[13]建立了半经验模型来预测部分饱和砂土中超静孔压的产生。在试验研究方面,Fattah等[14]通过物理模型试验,发现纯竖向振动引起的管桩桩周的超孔压可忽略;张亚国等[15]通过离心模型试验,研究了距管桩的水平距离和埋深对饱和黏性土中静压沉桩引起的桩周土体总应力和超孔压变化的影响;Azzouz等[16]采用压电侧向应力(piezo-lateral stress, PLS)装置测量了黏性土中沉桩阶段和随后固结阶段的桩身孔压;王永洪等[17]通过黏性土中的足尺静压PHC管桩贯入试验,确定了桩身不同位置处超孔压与上覆有效压力的比值。在数值模拟方面,钱峰等[18]通过ABAQUS对沉桩过程中的超孔压进行了数值模拟;孟振等[19]利用有效应力方法计算了修正剑桥(modified Cam-clay, MCC)模型Vumat子程序中的超孔压,并模拟了不排水条件下软黏土中沉桩施工对桩周土体的影响;桑松魁等[20]研究了沉桩过程中层状土中静压PHC管桩桩土界面处孔压随深度的变化规律,何耀辉[21]监测了压桩后土体的水平位移和超孔压随时间的变化规律,两者从沉桩过程和成桩后桩周土体的固结过程研究了沉桩施工对桩周土体的影响,并提出了合理解决沉桩挤土效应的措施。由此可见,沉桩施工过程分为沉桩过程和沉桩后桩周土体的固结或工程性质改变过程两个阶段,这种假设适用于渗透性较差的饱和黏性土,不适用于砂土等渗透性较好的土体。上述研究大多针对静压沉桩过程中桩周土体孔压的变化规律,而对静压沉桩后管桩桩周及桩端土体的超孔压时空分布特征和竖向有效应力变化规律缺乏研究。

本文通过现场原位试验和ABAQUS有限元软件对静压沉桩后PHC管桩桩周土体的固结过程进行研究,分析处于层状饱和黏土中的竖向受荷管桩引起的超孔压时空变化特征和桩端局部土体应力变化规律,并对比探讨不同竖向荷载工况下超孔压的空间分布特征,为静压沉桩引起的相关工程问题提供参考依据。

1 现场试验方案

现场试验在深圳市龙华区黏土地区进行,根据勘察结果,场地内的地层主要是人工填土层、第四系冲积层和第四系残积层,各土层物理力学指标见表1。该场地地下水埋深为0.3～4.0m。

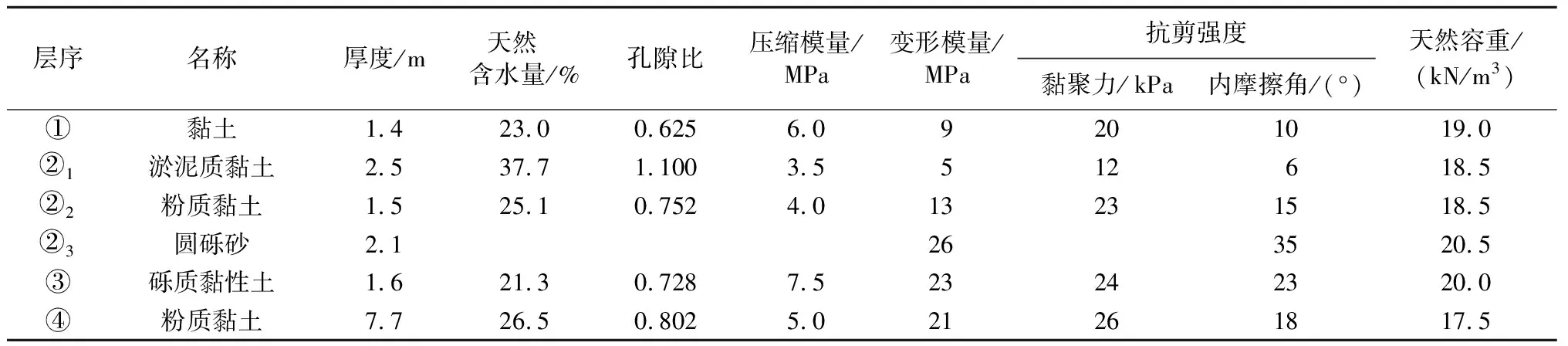
表1 土层物理力学指标

1.1 量测桩与监测仪器的布置与埋设

试验采用PHC-500AB-100型预应力高强混凝土管桩,管桩外径为500mm,壁厚100mm,单节桩长10m,施工方法为静力压入法。为精确获得沉桩后桩土界面、桩周层状土体和桩端底部局部土体中孔压随深度和平面距离的变化规律,在量测桩桩身表面安装AD-25微型孔压传感器和HC-16微型应力传感器,两种压力传感器的压力量程分别为0～100MPa和150kPa～100MPa,精度均为满量程的±0.1%。

为防止PHC管桩压入分层土时对传感器造成偏转和损坏,考虑到孔压传感器过小和土压力的方向性,选用直径12mm螺母、硅胶和橡胶塞与AD-25微型孔压传感器共同加工形成扩大头(图1(a)),选用1.2mm厚、15mm宽的薄钢片对试验中处于相同水平位置的HC-16应力传感器进行不同方向的固定(图1(b))。

图1 加工后的传感器

依据不同的埋深和径向距离,在量测桩外表面上的桩端至桩顶共布置了6个孔压传感器(U01～U06),与桩端距离依次为0、2、4、6、8、10m;还布置了3个应力传感器(P01～P03),与桩端距离分别为0.25、0.5、1m。另外为了获得桩端局部土体的超孔压变化规律和土体应力场,在桩端各埋设了1个孔压传感器(U07)和应力传感器(P04);埋设U08、U09和U10 3个孔压传感器和P05、P06两个应力传感器,以便获得水平方向距桩不同径向距离的孔压和应力变化,具体布置情况见图2。为较准确地将桩身以外的P05、P06与U08、U09、U10传感器布置在预定位置,采用自制螺旋掏土工具和内径为15mm、壁厚1mm的薄壁钢管钻孔,将传感器放入达到预计深度的孔洞中,并充填先前掏出的原状土。

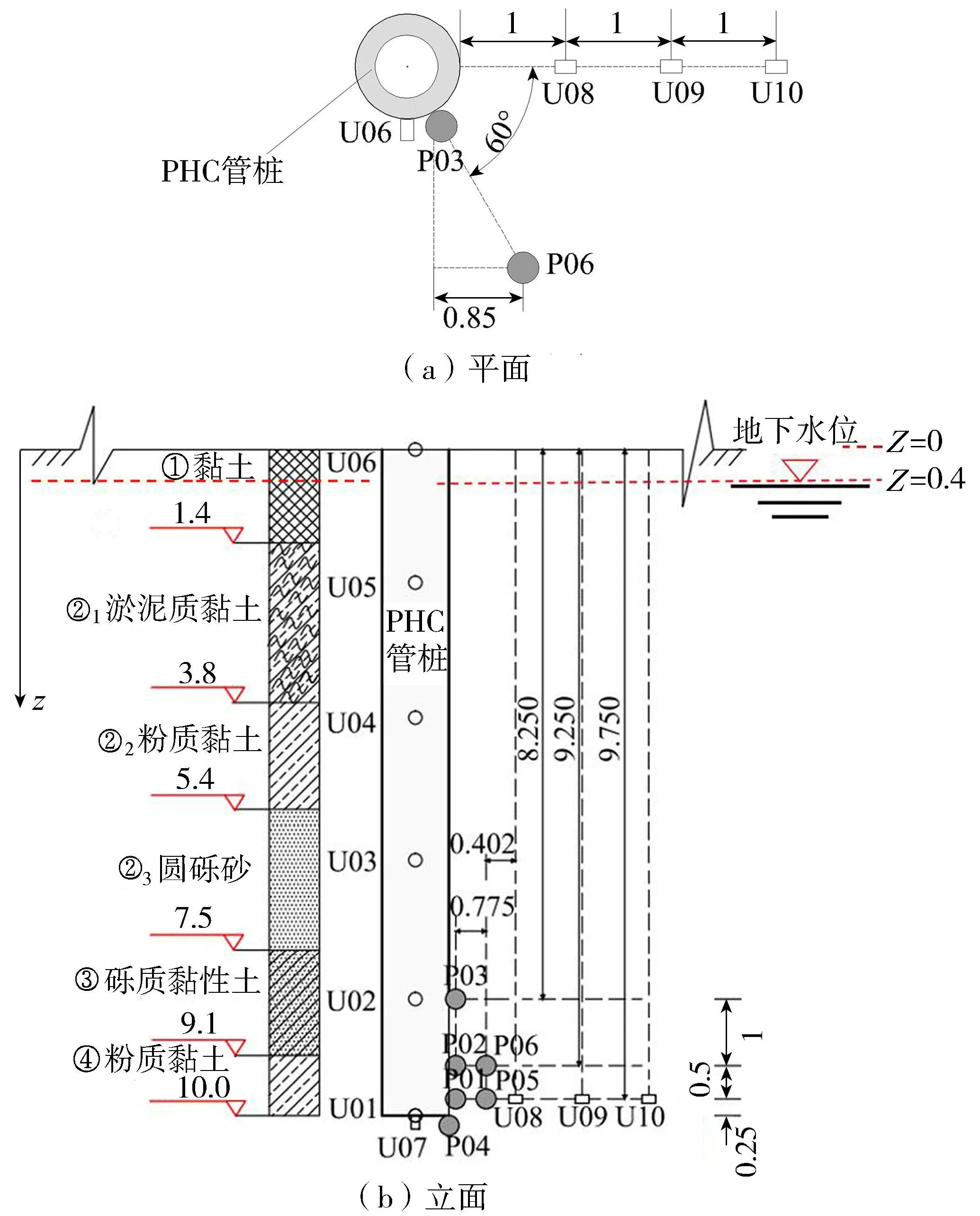
图2 量测桩周围传感器布置示意图(单位: m)

1.2 加载过程与数据采集

采用压力传感器、位移传感器、桩基静载测试分析仪和内径300mm的千斤顶等对量测桩进行竖向加载试验。量测桩的最大预估载荷为300kN,在其桩顶采用慢速维持荷载法进行竖向加载,每级施加30kN,当加载后桩顶沉降量小于0.1mm/h且连续出现2次时,视为达到稳定标准,才能施加下级荷载,重复此操作,直至量测桩荷载沉降曲线出现明显拐点可终止加载。使用YSV8316静态应变仪采集试验数据,可以实现16通道同时采集,频率为50Hz。

2 现场试验结果与分析

2.1 不同埋深处桩土界面超孔压变化

沉桩时在桩身表面测得的瞬时孔压增量Δu为超孔压,超孔压与静水压之和为桩土界面处的孔压。通过采集不同埋深H处孔压传感器的数据,可获得成桩后桩土界面超孔压的变化规律,结果如图3所示。其中处于桩顶位置的U06传感器因埋深很浅,测读时间短,无法测出U06传感器的有效值。

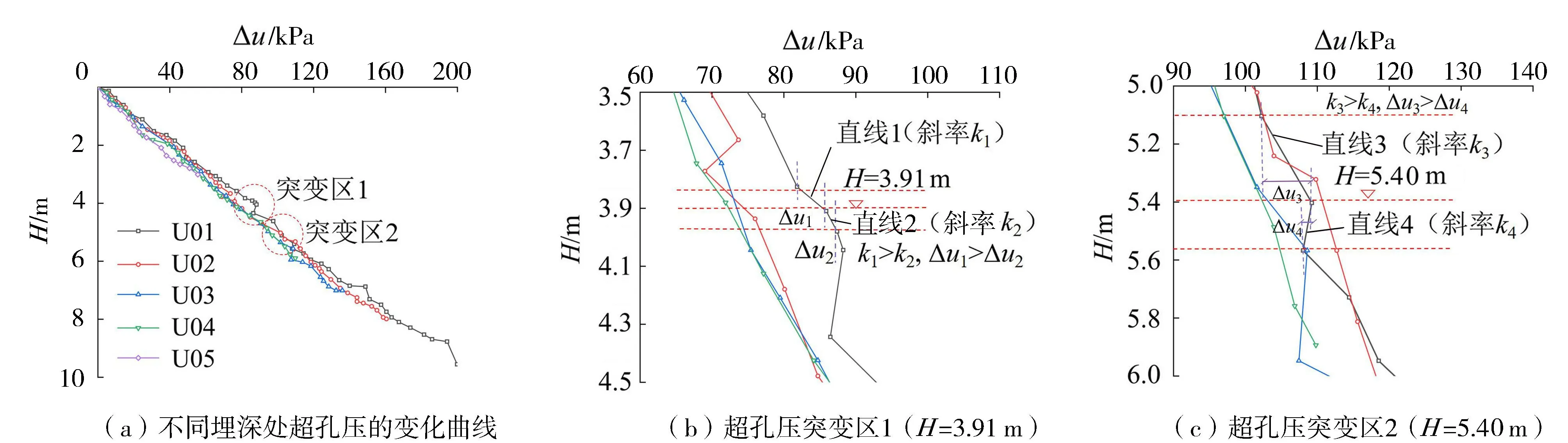
图3 沉桩过程中超孔压分布

由图3可知,不同埋深处桩土界面超孔压的分布曲线具有同样的变化规律,即桩土界面处超孔压均随着管桩埋深的增加近似呈线性增长趋势,且局部增长趋势随桩周特性不同的土层而发生突变。以布置在桩端的U01传感器为例,简要分析不同埋深处桩土界面超孔压的变化规律:超孔压在地下水位以上几乎为0,在地下水位以下随沉桩深度增加而急剧增大,其原因是桩端处发生剪切破坏时土体被挤压开裂,导致超孔压急剧增大。当桩端打入至3.91m和5.40m处时,超孔压的增幅小于桩端位于上一土层时的增幅,这是因为3.91m处为淤泥质黏土层和粉质黏土层的分界面,此处粉质黏土层的渗透性大于淤泥质黏土层;5.40m处为粉质黏土层和圆砾砂层的分界面,此处圆砾砂层的渗透性大于粉质黏土层;渗透性大的土层,有利于孔隙水的消散,致使桩端分别处于粉质黏土层和圆砾砂层时超孔压增大较慢,具体突变如图3(b)(c)所示;同理,当桩端打入至7.5～9.1m和9.1～10.0m时,桩端分别处于砾质黏性土层和粉质黏土层时超孔压增大较快。结果与桑松魁等[20]现场原位测试得到的规律相似。

2.2 桩土界面超孔压随时间的变化

以沉桩结束的时刻为起点,监测并采集沉桩后不同埋深处的孔压传感器数据,绘制出不同埋深处超孔压Δu随时间的变化曲线(图4)。由图4可知,初始时刻,不同埋深桩土界面处Δu基本处于各自的最大值,即此刻从桩端(H=10m)到桩顶(H=0m)的Δu最大值依次为193.2、49.8、40.5、31.7、25.8、17.6kPa;前5天不同埋深处的Δu基本无变化,仍大致处于各自的最大值。第5天后Δu开始减小,这预示着超孔压开始消散;第5～6天Δu减小速度很快,第6～20天Δu减小速度变慢,并伴随着小幅度升降波动,其中在H=0m处,即桩顶附近土层的Δu减小到0kPa,其原因是桩顶处的土层受扰动较小,其他埋深处的Δu均不超过30kPa;第20～30天不同埋深处的Δu随时间的推移逐渐趋于稳定,桩周地基土慢慢进入休止期,即成桩后第30天,各土层的超孔压基本消散完毕。

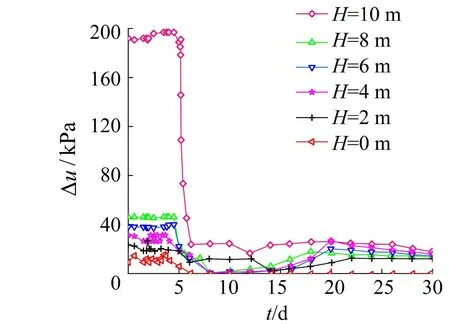
图4 超孔压变化曲线

2.3 上覆竖向有效应力随时间的变化

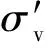
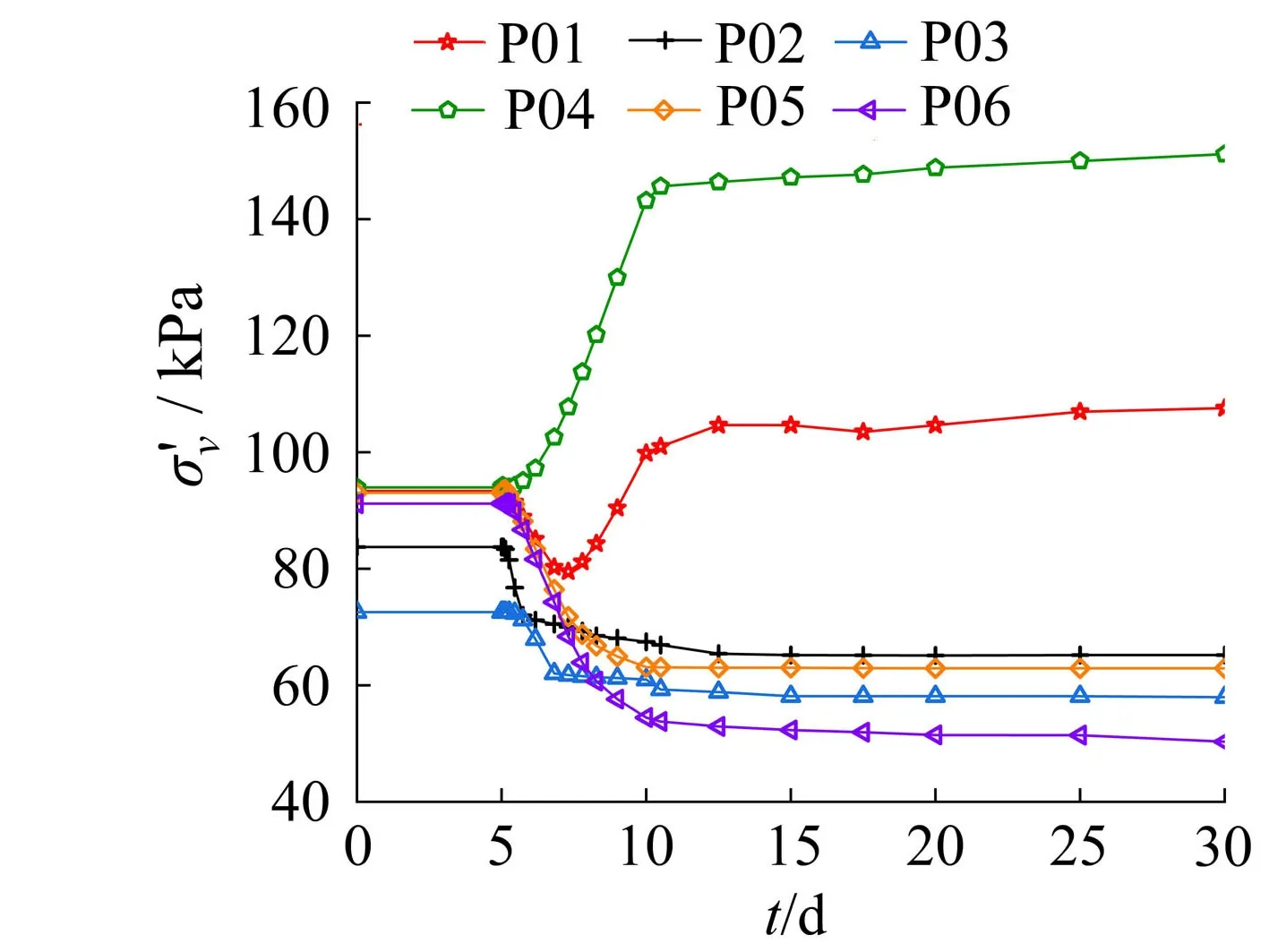
图5 上覆竖向有效应力变化曲线

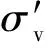
3 理论分析

3.1 沉桩引起超孔压变化的机理

沉桩过程中管桩桩周黏土体产生塑性区,此时在不排水条件下的受挤压过程中,水和土颗粒不易压缩导致孔压升高。在成桩后饱和土渗流固结过程中,超静孔压即孔隙水上的孔压u逐渐消散,饱和土中任意面上的总应力σ转移到土骨架上,竖向有效应力σ′逐渐增大,u和σ均是时间的函数,即u=f1(t),σ′=f2(t)。由外荷载引起的u随时间的增长而逐渐消散,σ′、u和σ三者之间的关系为[11]

σ′=σ-u

(1)

结合水力压裂和孔穴扩张理论[20],推导出沉桩过程中在桩土界面处竖向开裂和水平开裂时超孔压的计算公式分别为

(2)

(3)

其中Ir=G/cu=Eu/2(1+ν)cu

式中:Δuhm,S、Δuhm,P分别为深度h桩土界面m上竖向开裂和水平开裂时的超孔压;cu为不排水抗剪强度;Ir为刚度指数;K0为土侧压力系数;G为弹性剪切模量;Eu为不排水三轴试验的初始切线模量;ν为土体的泊松比。

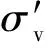
(4)

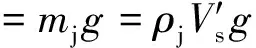
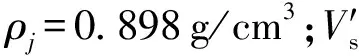
式(4)的展开推导同文献[22],对单位面积的土体,得到修正后的上覆竖向有效应力为

(5)

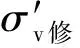
3.2 MCC模型不排水分析方法

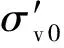
(6)

式中γ′为土体的有效容重。考虑到在水平方向无变形,K0=ν/(1-ν)。

(7)

其中M=6sinφ′/(3-sinφ′)

式中:M为临界状态线的斜率(临界状态应力比);φ′为土体有效内摩擦角。

根据MCC模型在e-lnp′ 坐标系上的等向压缩固结曲线[25],其二维状态边界面的一般方程为

(8)

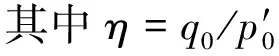
式中:e0为初始孔隙比;λ为塑性体积模量对数(压缩曲线的斜率);κ为多孔介质体积模量对数(回弹曲线的斜率);η为初始应力比。式(8)化简得:

(9)

通过无侧限抗压强度试验求饱和黏土的不排水剪切强度cu,在径向应力σr=0、侧向应力σl=2cu时的偏应力q0为

q0=σl-σr=2cu

(10)

不排水条件下[25-26],MCC模型中偏应力q0亦可表示为

(11)

由上述各初始应力条件和式(10)(11),根据MCC模型理论,土体中的不排水剪切强度cu为

cu=(M/2)exp{[(1+e1)-(λ-κ)ln2-(1+e0)]/λ}

(12)

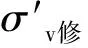
4 有限元数值模拟

4.1 数值模型构建

采用ABAQUS 建立三维圆柱模型并进行计算,为节省运算时间,据其对称性建立1/4模型来分析不同桩顶荷载作用下的超孔压。模型的尺寸参数及土体参数参照现场原位试验的数据来设置,桩径为0.5m,桩长为10m,桩体的弹性模量Ep=30 GPa,泊松比νp=0.3,桩周土体为半径10m、高20m的1/4圆柱体。采用MCC模型作为土体本构模型,桩体采用刚体模拟。其他土层重要参数如表1和表2所示。

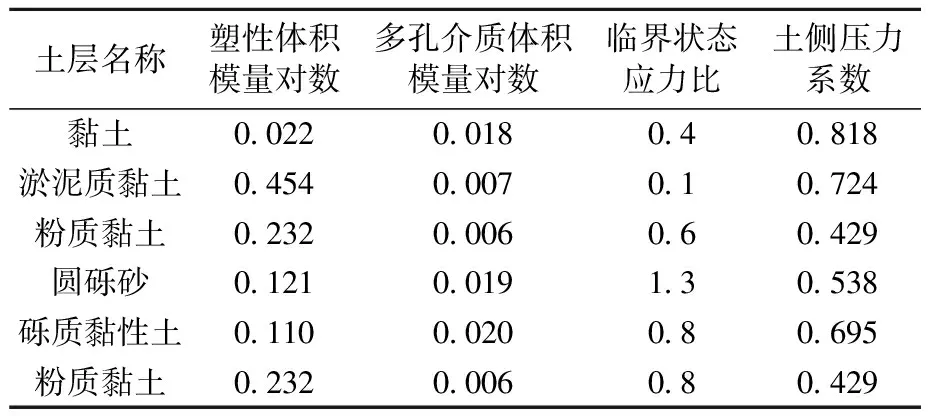
表2 各土层参数

根据上述条件对所建立的三维圆柱模型进行网格划分(图6),得到16028个实体单元,选取C3D8作为桩体单元,C3D8P作为土体单元,分析桩身的应力和不排水条件下桩土渗流应力耦合作用;将模型底部和顶面分别设为固定边界和自由边界,对侧面边界施加水平约束;模型建立后,先分析初始应力场,然后导入自编的子程序VOIDRI对初始孔隙比进行预定义,最后在桩顶施加分级竖向荷载,以此来模拟沉桩后外荷载作用下的管桩桩周层状土体的渗流固结过程。

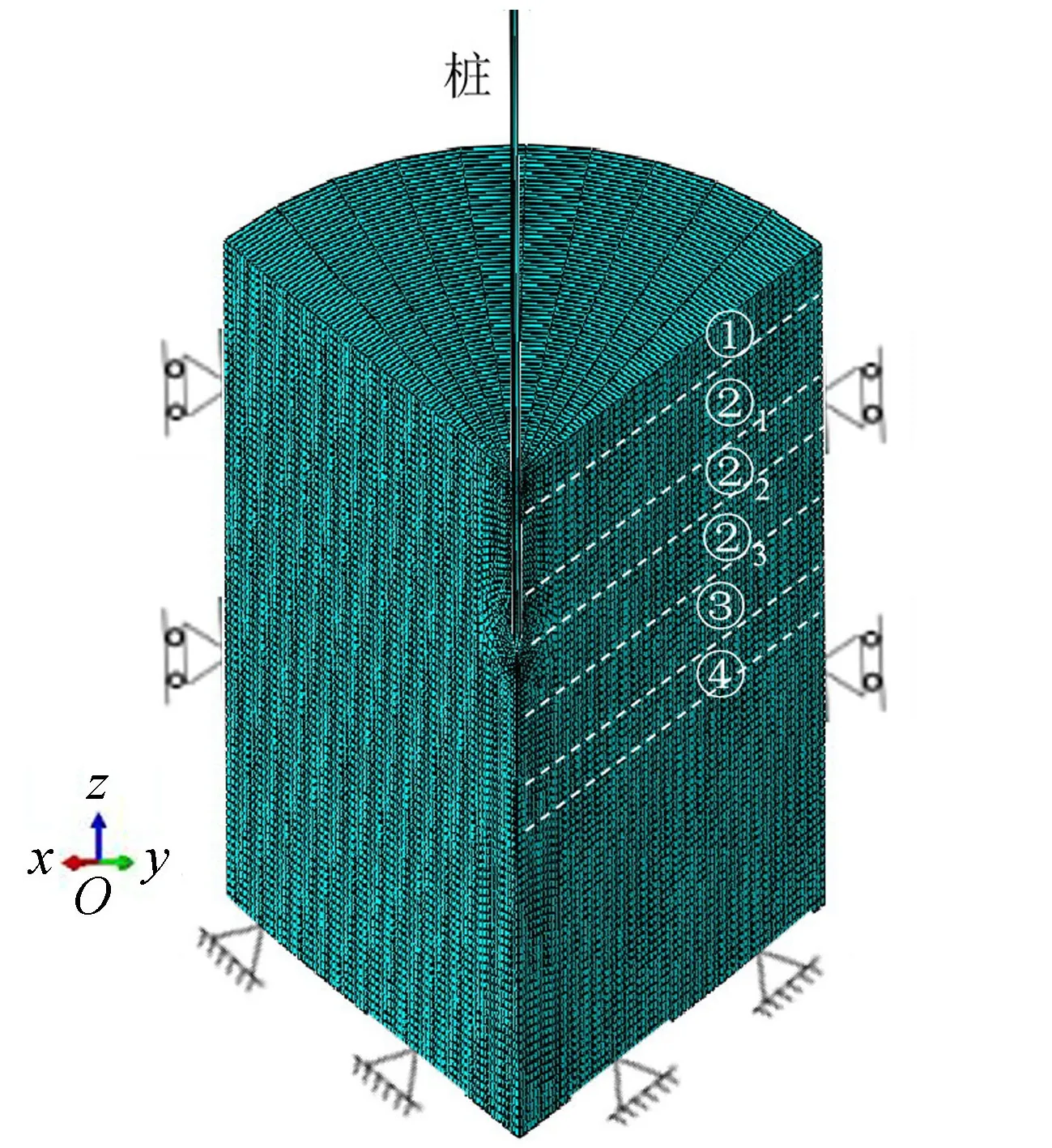
图6 有限元模型

4.2 模型验证

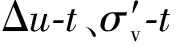
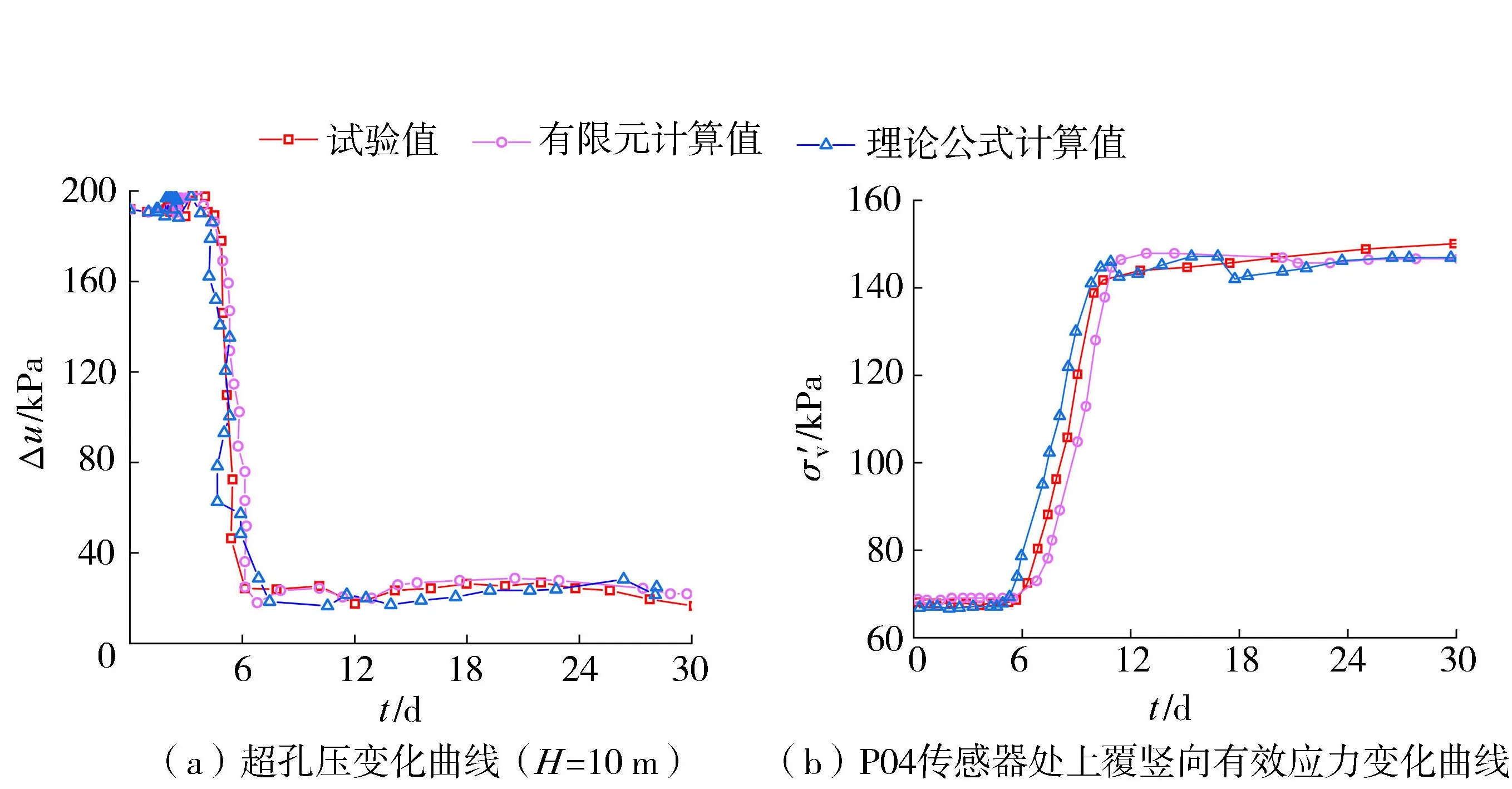
图7 模型对比验证曲线

4.3 荷载条件下的超孔压变化

对建立的模型桩桩顶施加分级荷载,得到沉桩在不同荷载p作用下桩周及桩端下部土体的超孔压分布云图(图8),可见超孔压最大值出现在桩端底部,并随着距桩心径向距离的增大而逐渐减小。当对桩顶分别施加60、90、120、150kN荷载时,最大正孔压依次为66.280、11.640、6.383、4.285kPa,最大负孔压依次为-23.320、-3.232、-1.655、-1.065kPa。此外,桩端下局部土体产生的超孔压区域在水平方向和垂直方向上比前一级荷载变大。

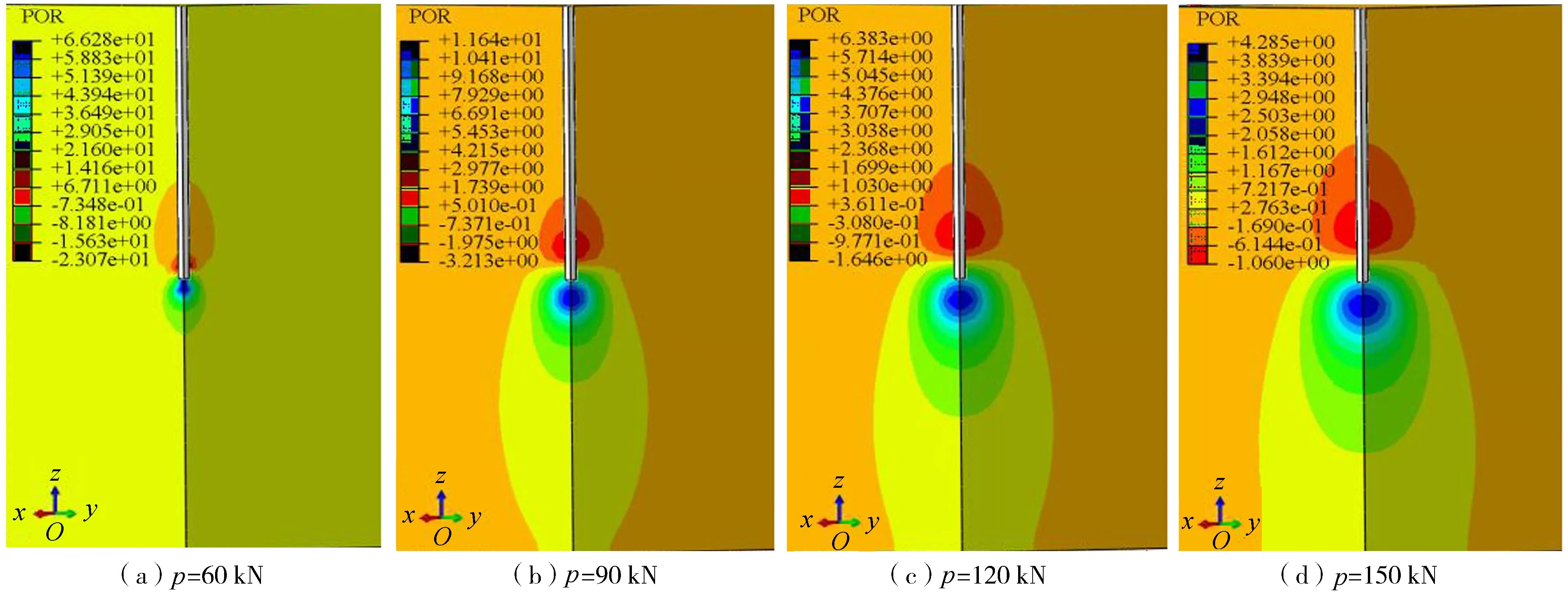
图8 不同桩顶荷载作用下超孔压变化云图(单位: kPa)

从图8可看出桩侧中下部产生了负的超孔压,是因为静压沉桩后产生的挤土效应,距模型桩较近的群桩区域内后压桩可能会对先压桩产生浮桩作用,桩端受到向上荷载作用的同时,渗透系数小、含水量大且处于卸荷状态的桩侧软黏土体中会产生负的超孔压;从整体上看,桩顶施加荷载逐渐增大的同时,桩端土体产生的超孔压区域也逐渐变大,且桩端下部区域较上部更大,最大正孔压和负孔压值逐渐变小,表明超孔压随桩顶施加荷载的增大而逐渐消散,桩端和桩侧靠下土体有效应力值逐渐增大,这是由于静压沉桩和沉桩后对桩顶的竖向加载可以在桩周土体中产生可能超过土体静水劈裂压力的超孔压。另外在对桩顶进行竖向加载时,桩对土的剪切作用使土体体积膨胀,较高的超孔压和沉桩施工会使桩侧土体发生劈裂现象,且可通过劈裂裂缝使超孔压快速消散。

图9是不同桩顶荷载作用下,水平方向上距离桩心不同位置的超孔压变化云图。根据桩周孔压传感器所在位置,选取埋深H=10m、土体半径为5m范围内的1/4圆柱面分析其超孔压变化规律。从图9可看出,当在桩顶分别施加60、90、120、150kN荷载时超孔压最大值依次为61.600、7.880、4.420、3.060kPa,超孔压最小值依次为-0.200、0.000、0.000、0.010kPa。整体从某一平面上看,水平方向上的超孔压随着荷载p的增大而逐渐减小。各级荷载下H=10m的桩周土体平面上,超孔压在水平方向上随着离桩心越来越远而逐渐减小,且水平方向超孔压最大值均小于竖直方向上的超孔压最大值,这也意味着随着地基土的渗流固结,超孔压逐渐消散的同时,桩端局部土体竖直方向有效应力比水平方向上有效应力更大,随时间增长更快。成桩后,随着时间的推移,当某一时刻的超孔压消散完毕,有效应力不再增大时,意味着地基土开始进入休止期。

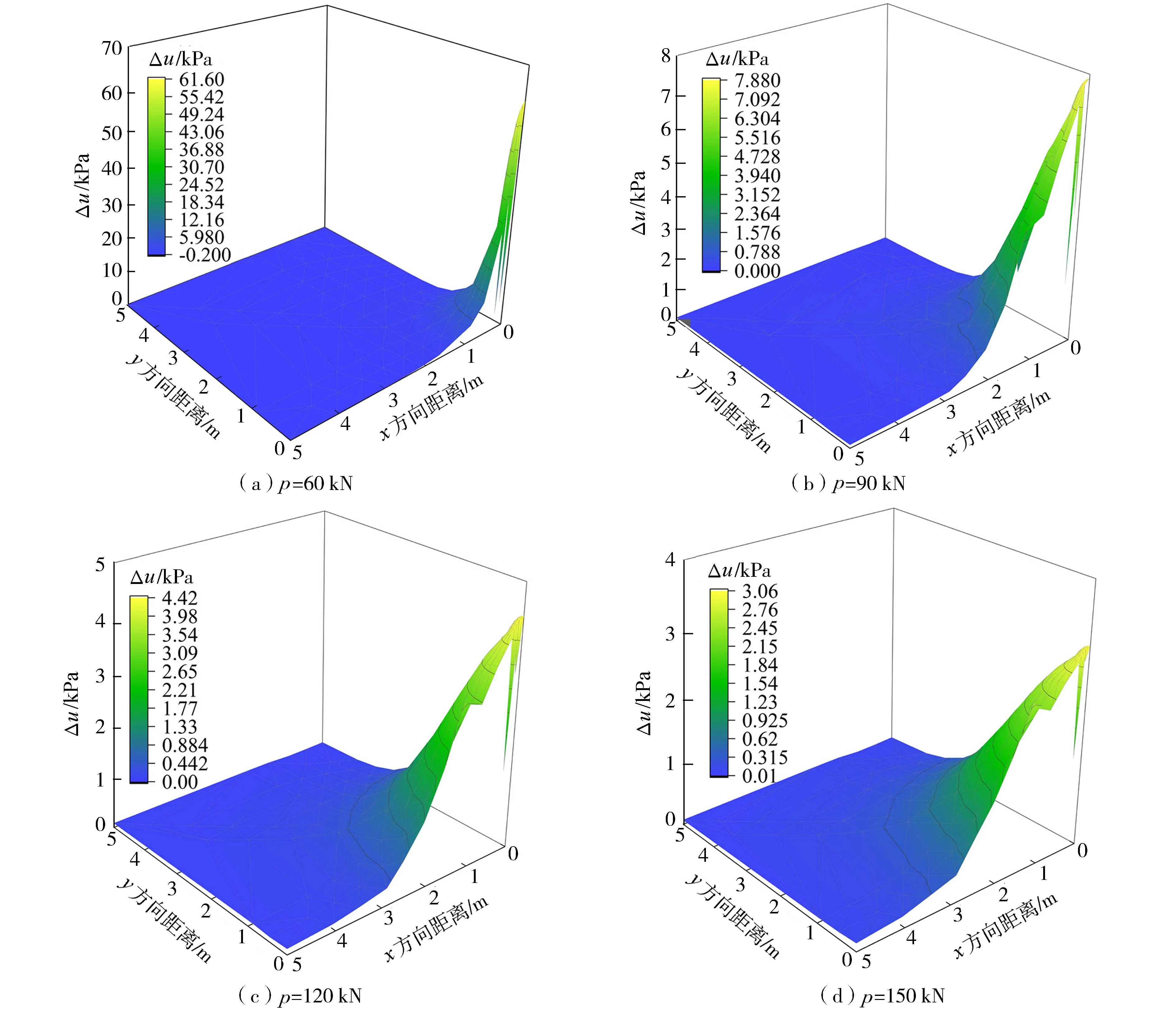
图9 距离桩心不同位置的超孔压变化云图

5 结 论

a.超孔压随着管桩埋深的增加而呈逐渐增大趋势,并且超孔压增大速率与桩周土层渗透性呈负相关关系。

b.沉桩结束后的初始时刻,越接近桩端的超孔压最大值越大,之后便快速下降并趋于稳定,即超孔压随时间推移基本消散完毕。在桩端局部土体中,越接近桩端的初始上覆竖向有效应力越大,随时间呈逐渐增大的趋势;反之,远离桩端的土体呈相反变化规律,但最终都趋于稳定,即上覆竖向有效应力不再增大和减小,即成桩后30d地基土处于休止期。

c.在不同桩顶荷载作用下,桩端底部的超孔压最大,桩侧中下部超孔压出现负值,即竖直方向上距离桩端越近,超孔压越大,同一水平方向上离桩心距离越远,超孔压越小;随着桩顶荷载的增大,靠近桩端和桩心的超孔压最大值逐渐减小。