竹节桩复合地基沉桩施工超孔隙水压力研究
叶俊能, 周 晔, 朱瑶宏, 刘干斌
(1.宁波市轨道交通集团有限公司, 浙江 宁波 315012; 2.宁波大学岩土工程研究所, 浙江 宁波 315211)
在饱和软黏土地层中进行沉桩时,由于沉入挤压作用可使土的结构性发生破坏,产生很大的初始超静孔隙水压力,会对周围环境产生很大的影响,这已经引起广泛重视[1]。
理论上,王旭东和王伟等[2-3]给出了沉桩引起的初始超孔隙水压力沿深度线性增加和沿径向在桩周弹、塑性区内连续分布的简化计算公式,以Biot固结理论为基础,进一步推导并获得了超孔隙水压力消散的三维解析解,分析了桩群不同桩距、不同入桩顺序对超静孔隙水压力的影响。马林等[4]从空间圆孔扩张理论出发,考虑到沉桩速率,提出了超静孔隙水压力随径向和深度方向变化的分布公式。苗永红等[5]在现有理论解基础上,考虑土体的应变软化和圆孔扩张,结合Henkel公式推导了沉桩引起的初始超孔隙水压力理论修正解。陈文等[6]通过静压桩在不同黏土中贯入的离心模型试验,对桩体贯入饱和黏土时的土体位移和初始超孔压的空间分布情况进行了研究。廖幼孙等[7]基于室内模型试验,对无孔管桩群桩和3种布孔方式的有孔管桩群桩沉桩时引起的超孔隙水压力进行了监测,分析了沉桩顺序、布孔方式等因素对超孔隙水压力时空消散的影响。唐世栋等[8-9]通过对桩基施工过程中实测资料的分析,探讨了沉桩时单桩、群桩周围土中产生的超孔隙水压力的大小、分布及影响范围,与理论解进行了对比,并对超孔隙水压力的产生、分布和变化趋势进行了探讨。张忠苗等[10]通过对杭州萧山某工地的沉桩挤土效应进行现场监测,得到超孔隙水压力的动态变化规律。钱峰等[11]通过饱和黏土中静压沉桩模型试验,模拟了预制混凝土桩的施工过程,重点监测了孔隙水压力、桩侧土压力、地面隆起量随桩的贯入深度和距桩轴不同距离的变化规律。
近年来有大量异型预制桩应用于实际工程中,例如竹节型预应力管桩。在沉桩过程中,由于竹节间的空隙无法被周边的土体填满,从而形成多节空腔,阻碍了竹节上下两个空腔内水体的流动,对竖向超静孔隙水压力的消散产生一定的影响,现有计算理论无法考虑这一影响,竹节型预应力管桩沉桩施工超孔隙水压力变化规律有待研究。为此,本文结合宁波轨道交通4号线东钱湖车辆段竹节桩复合地基沉桩施工,开展超孔隙水压力现场测试,并在王伟等[3]的研究基础上,考虑竹节桩竹节间空隙对竖向超静孔压分布影响,建立竹节型预应力管桩超孔隙水压力计算公式,为竹节型预应力管桩技术的推广和应用提供参考。
1 现场测试方案
1.1 工程概况
宁波轨道交通4号线东钱湖车辆段地貌类型属于滨海淤积和冲湖积平原,场地地层分布情况及各土层物理力学参数见表1。

表1 土层分布及力学参数表Table 1 Soil distribution and mechanical parameters
1.2 试验方案设计
本次竹节桩复合地基试验共设置3个工况,每个工况含竹节桩16枚,正方形布置(4×4),桩间距分别为1.8,2.0,2.2 m,桩长分别为20,22,24 m。各工况竹节桩混凝土强度等级、桩长、桩间距如表2所示。

表2 各工况竹节桩试验参数表Table 2 Test results of nodular piles under various conditions
在3个工况中分别选择2桩之间、4桩中心均布设3个孔隙水压力传感器测点,以测试打桩前后孔隙水压力的变化规律。工况一测孔编号为1,4,7,工况二测孔编号为2,5,8,工况三测孔编号为3,6,9(图1)。各测点从2 m以下开始按3~7 m间距布设,布设深度及间隔如图2所示。

图1 孔隙水压力测试平面布置示意图Fig.1 Plane layout of the pore water pressure test
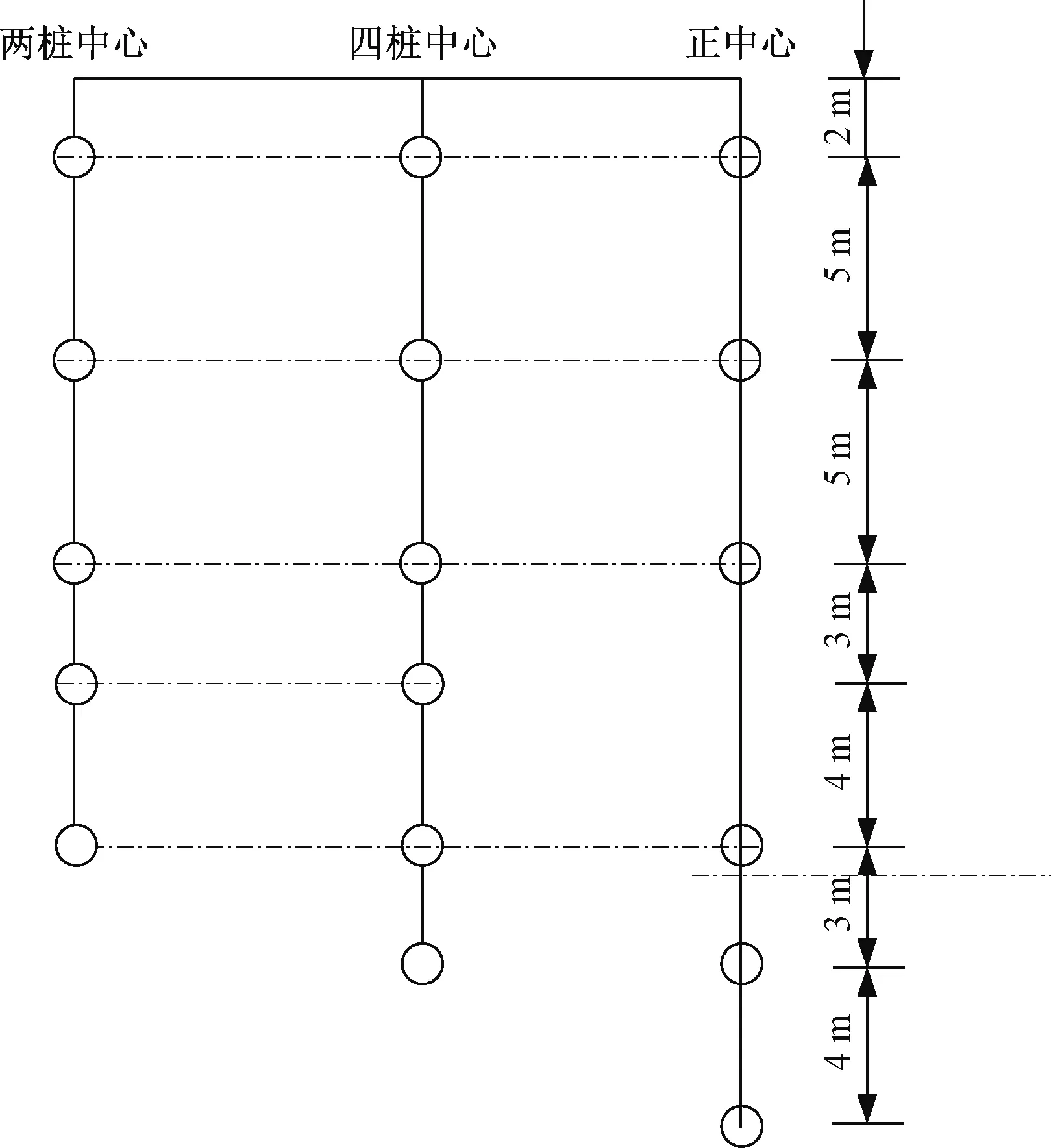
图2 竖向孔压水压力测点布置示图Fig.2 Location of the measurement points for vertical hole pressure water pressure
打桩前,钻孔布设完成后采集各点孔压初值;打桩过程及打桩后持续采集孔压值,直至试验结束。孔隙水压力传感器3需测试4桩复合地基静载荷试验全过程的孔压变化数据。
2 理论计算模型
由于沉桩速度较快,竹节间的空隙无法被周边的土体填满,从而形成许多空腔(图3),这些空腔内积满了大量的因桩周土体固结而排出的孔隙水。假设第n个空腔中的最大超静孔压可取土体出现劈裂的极限压力Pn,为超静孔压Pcn与静水压力Pjn之和。

图3 竹节桩成桩后空腔分布示意图Fig.3 Schematic diagram of cavity distribution after nodular piles are piled
桩体竹节可阻碍上下两个空腔内水体的流动,这种阻力受制于桩周土体与桩体表面的摩擦及桩体下沉期间对桩周土体的扰动,假设:
(1)当竹节上下两个空腔的孔压差值小于竹节阻力时,两个空腔内的水体不通过竹节面发生渗透。
(2)当两个空腔内的孔压差值大于竹节阻力时,两个空腔内的水体通过竹节面发生渗透,直至两个空腔内的孔压差值等于竹节阻力。
(3)竹节阻力随深度的增加而呈线性增加,即:
qs=q0+kz
(1)
式中:qs——竹节阻力;
q0——竹节固有阻力;
k——与深度有关的竹节阻力线性增加系数;
z——深度。
(4)沉桩刚完成时,桩体桩底以下土体不发生挤土,即无超静孔压发生。但桩底上部的最大超静孔压Pcm会突破竹节阻力进行渗透,进而使桩底部位也具有较大的超静孔压Pb,其分布规律如图4所示。
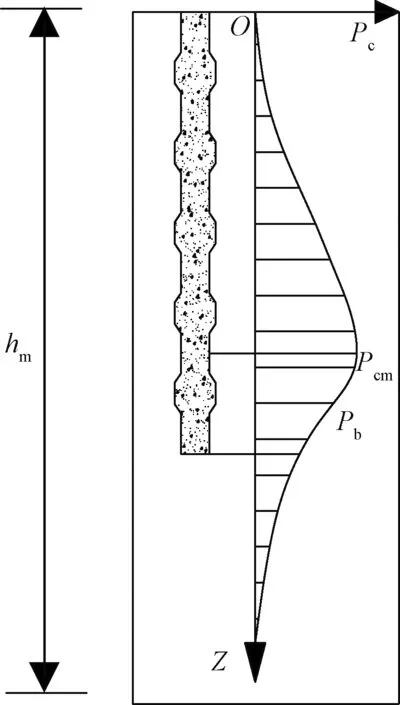
图4 竹节桩沉桩后超静孔压竖向分布曲线Fig.4 Vertical distribution of the excess static pore pressure
2.1 径向孔压分布
根据唐世栋等[7]的研究结果可以得到单桩沉桩引起的超静孔压径向分布,在桩身表面有:
(2)
塑性区半径为:
(3)
式中:E——土的弹性模量;
μ——土的泊松比;
r0——桩半径。
Henkel 孔隙水压力参数α与Skempton 孔隙水压力参数A之间有如下关系α=0.707(3A-1)。抗剪强度计算公式为Cu=c+rztanφ,其中c为黏聚力,γ为土体重度,z为深度,φ为内摩擦角。
2.2 竖向孔压分布
当地层中的土体因超静孔压受到挤压时,所能承受的最大超静孔压可考虑出现劈裂的极限压力确定[12]:
(4)
式中:Pn——劈裂的极限压力。
在竹节桩沉桩期间Pn主要是超静孔压与静水压力之和,即Pn=Pcm+Pjn,由此可得出最大超静孔压的计算公式为:
(5)
式中:Pjn——静水压力;
Pcm——最大超静孔压;
γ——上覆土体重度;
z——计算深度;
φ——土的内摩擦角;
c——土的黏聚力。
当沉桩产生的超静孔压Δumax>Pcm时,土体将在超静孔压的作用下发生劈裂,超静孔压随即减小,直至Δumax≤Pcm为止,因此由式(2)和(5)可以设定最大超静孔压深度hm满足如下关系:
(6)
式(6)为超越方程,无法得到解析解,但可以通过数学软件计算得到数值解。为此,对竹节桩沉桩期间的超静孔压竖向分布应做离散化计算。
(1) 当Pn大于极限超静孔压时,Pn在劈裂作用的影响下,其表达式为极限超静孔压的计算公式,即Pn>Pcm时,有:
(7)
(2) 当Pn小于或等于于极限超静孔压,且计算深度小于或等于最大超静孔压深度时,即Pn≤Pcm、z≤hm,考虑竹节阻力的影响。
当Pn+Pjn>Pn-1+Pjn-1+qsn时,
Pn=Pn-1+Pjn-1-Pjn+qsn
(8)
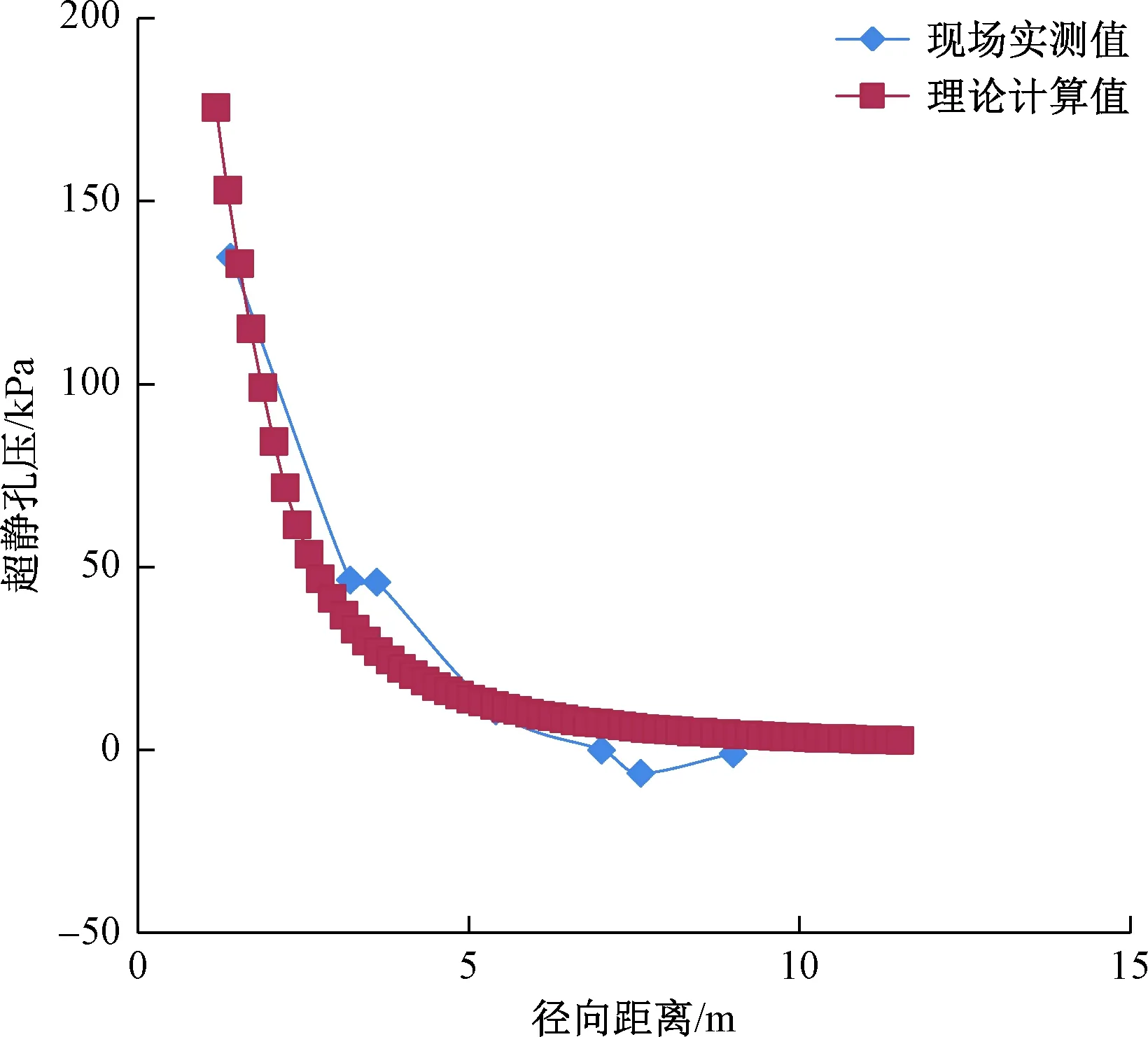
当Pn+Pjn (9) (3)当Pn≤Pcm且z>hm时,设Pm=Pcm,m为最大超静孔压所在的桩节数。 (10) 王伟等[3]从水力连续条件出发,通过对Biot方程进行近似求解,得出任意时刻的超静孔隙水压力表达式: (11) 式中:U(t)——t时刻超静孔隙水压力数值; Δu0——超静孔隙水压力的初始分布,即初始超静孔隙水压力; a——影响半径与桩径的比值,即a=R/r0(R为影响半径,r0为桩半径); ρ——计算点到桩中心的距离与桩半径的比值,即ρ=r/r0; cv——土的固结系数; bsj1——一阶贝塞尔函数; bsj0——零阶贝塞尔函数; λi——零阶贝塞尔函数的第i个零解。 将Δu0从上述式(11)中提出,化简如下: U(t)=TΔu0 (12) (13) 当t=0时,即初始时刻,T的表达式退化为: (14) 式中贝塞尔函数取前10项即可满足工程计算需要,即i值取1~10。经计算,式中的T≈1。由此可见,T为超静孔压随时间消散的因子项。 (1)沉桩后超静孔压最大值 各测孔超静孔压最大值测试结果如表3所示,因沉桩期间重型施工机械碾压了部分传感器线缆,且传感器又位于桩基下部,无法实施补救,故而造成部分测点损坏,整体测点存活率为92%,该存活率不影响试验数据分析。 表3 竹节桩超静孔压最大值统计表Table 3 Maximum static pore pressure of nodular piles 从表3中可以看出,1.8 m桩间距产生的最大超静孔压为378.7 kPa,2.0 m桩间距产生的最大超静孔压为288 kPa,2.2 m桩间距产生的最大超静孔压为352.1 kPa,由于这些最大超静孔压是因群桩效应叠加而成, 3个桩基施工区域相互间距离仅2 m左右,所以这种叠加既有区域内也有区域间的叠加。 图5 桩间距为2.0 m工况时各测孔超静孔压时程曲线Fig.5 Changes in pore pressure of the monitoring hole when the distance of the piles is 2 m (2)沉桩后超静孔压时程变化 以2.0 m间距工况为例,各测孔超静孔压时程曲线如图5所示。 由图5可得出:超静孔压随着竹节桩下沉而增大,沉桩完成后孔压随时间缓缓消散,需要引起重视的是沉桩当日孔压变化非常大。根据现场实测,发现最大超静孔压一般出现在沉桩完成后15~30 min内。 (3)沉桩后超静孔压分布 以2.0m间距工况为例,超静孔压沿径向分布如图6所示,可以看出,在不同深度,超静孔压沿径向呈指数形式衰减,在8 m左右超静孔压趋于零。在距桩中心不同距离,超静孔压沿深度方向分布如图7所示,可以看出,沉桩后超静孔压竖向随着深度的增加而逐 图6 超静孔压径向分布Fig.6 Radial distribution of the excess pore pressure 图7 超静孔压竖向分布Fig.7 Vertical distribution of the excess pore pressure 渐增加;最大超静孔压的出现点位于桩底以上的位置,大约在20 m深度处,20 m深度以下开始逐渐减小;地表区域的超静孔压随深度变化较小,桩底区域的超静孔压随深度变化较大。 利用工况二超静孔压测试数据与理论计算(按单桩考虑,沉桩完成后1 d开始计算,参数见表4)结果进行对比。 表4 超静孔压数据对比分析参数表Table 4 Contrastive analysis of parameters of the excess static pressure data 为避免浅部地层孔压受地面施工及其它地表水体的影响,选取2#测点,对其超静孔压竖向分布及19 m深径向分布进行分析,同时为了避免群桩效应叠加,仅分析第一根桩(①号桩,图1)施工引起的超静孔压变化。 图8 超静孔压径向分布数据对比图Fig.8 Comparison of radial distribution data of the excess static pore pressure (1)超静孔压径向分布对比 在工况二区域,第一根竹节桩沉桩时桩周19 m深处超静孔压分布规律如图8所示,其中理论值由式(2)计算得到,可以看出,理论计算结果与实测结果较为吻合,式(2)可以较好地描述宁波软土地区竹节桩下沉产生的超静孔压的径向分布。 图9 超静孔压竖向分布数据对比Fig.9 Comparison of vertical distribution data of the excess pore pressure (2)超静孔压竖向分布对比 利用式(7)~(10)计算得到距桩心2#测点超静孔压沿深度分布结果如图9所示,将实测结果绘于图9以进行对比,可以看出,理论计算结果与实测结果较为吻合,式(7)~(10)可以较好地反映竹节桩沉桩后的超静孔压竖向分布。 (1)由于竹节桩间距较小,超静孔隙水压力有叠加效应,1.8 m桩间距产生的最大超静孔压为378.7 kPa,2.0 m桩间距的最大超静孔压为288 kPa,2.2 m桩间距的最大超静孔压为352.1 kPa。 (2)超静孔压随竹节桩下沉而增大,最大超静孔压一般出现在沉桩完成后15~30 min内。在不同深度,超静孔压沿径向呈指数形式衰减,在8 m左右超静孔压趋于零,最大超静孔压的出现点位于桩底以上约2 m位置。 (3)考虑竹节桩竹节间空隙对竖向孔隙水压力的影响建立的孔压计算结果与实测结果较为吻合,可以较好描述竹节桩施工引起的超孔隙水压力分布。2.3 孔压时程分布
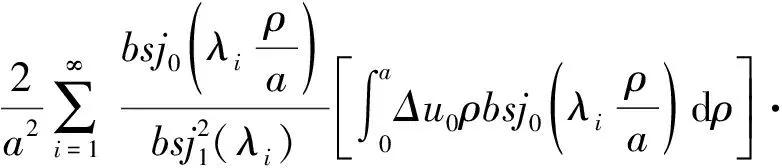
3 试验与计算结果分析
3.1 测试结果



3.2 试验与理论计算对比


4 结论

