近海废弃物收集系统压缩装置的疲劳寿命分析＊

青岛科技大学机电工程学院 青岛 266061

0 引言

当前，我国机械装备制造业迅猛发展，工艺水平得到长足进步，对装备的耐疲劳性提出了更高要求，故对机械装备的疲劳寿命研究具有重要意义[1]。一些科研机构及公司着手研究船体装备的疲劳寿命，Vedeler首先提出了船体疲劳强度的危害性[2]；Jordan 和Cochran对多艘正在服役船舶进行检测，在多艘船舶的关键区域发现了疲劳裂纹[3，4]；Song R等基于概率断裂力学理论提出一种双体船简化疲劳分析方法[5]；CCS的王然章川等人对船体结构疲劳强度计算的简化方法进行了研究[6]；蒋志岩对船体结构疲劳评估过程中的应力分析方法进行了探讨和比较，并通过有限元软件对热点应力的插值方法和有限元建模原则进行了研究[7]；顾学康、沈进威对非线性载荷的计算及其对疲劳损伤的影响进行了研究[8]。

由此可知，目前国内外针对船体结构的疲劳寿命研究较多，而对船体装置内部结构的疲劳寿命研究较少[9]。在近海废弃物收集船的压缩装置中，推板是实现压缩和推送垃圾的重要部件。压缩装置在工作过程中，推板会承受变化的动载荷，并在其作用下产生动态应力。当推板运行到保压阶段时，疲劳强度会降低，产生疲劳裂纹[10]，最终有可能导致推板发生断裂破坏。因此，有必要对推板进行疲劳寿命分析，确保推板结构在满足强度和刚度要求的基础上，达到可靠性和寿命要求。

1 压缩装置的结构

近海废弃物收集系统中的压缩装置主要由滑轨、进料斗、推板、液压缸、压缩舱体等组成，压缩装置结构示意图如图1所示。推板由板材制成，整体呈折面形，存在一个倾斜的支撑面；推板的侧面设置3个液压缸基座安装点，并通过焊接形式连接推板与液压缸基座；左右两侧布置滑轨接触口，并将推板与滑块整体焊接；推板底部施加3个排水孔，排水孔贯穿整体推板。压缩装置推板结构的三维模型如图2所示。

图1 压缩装置结构示意图

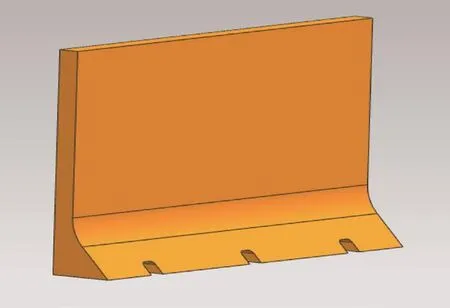
图2 推板三维模型

2 推板的静力学分析

静力学分析为推板疲劳寿命预测提供应力应变历程结果，确定疲劳问题较严重的部位[11]。静力学分析结果的可靠性将影响推板疲劳寿命预测结果的准确性，故有必要进行静力学分析。利用Ansys Workbench仿真平台对推板进行静力学仿真分析，首先将推板三维模型导入仿真平台，并对模型进行网格划分；然后依据推板的受力情况对模型施加载荷与约束；最后对模型的仿真分析进行求解，得到推板在理论载荷和约束下的变形和应力云图，完成静力学仿真。

2.1 理论基础与参数设置

1）理论基础

采用有限元法对结构进行静力学分析，对整体结构进行受力分析和结构简化,利用离散化的方法把简化的连续结构看作许多单元组件。对每个单元建立刚度方程,对整体结构建立平衡方程[12，13]。通过研究物体在力系作用下的平衡规律,确定静力学分析理论公式为

式中：[K]为刚度矩阵，{x}为节点位移矩阵，{F}为戴荷矩阵。

2）参数设置

设置材料属性，选择推板材料为Q345，其抗拉强度为490 MPa，屈服强度为345 MPa，弹性模量为2.06×105MPa，密度为7.85×10-6kg/mm3，泊松比为0.28。将有限元模型导入Ansys Workbench仿真平台，对模型划分网格，将载荷和约束施加于推板，推板的受力主要有执行液压缸对推板的推力、废弃物对推板的作用力、废弃物对倾斜面的作用力等。如图3所示，在液压缸基座B、C、D处分别施加载荷，在推板A点处设置固定约束。

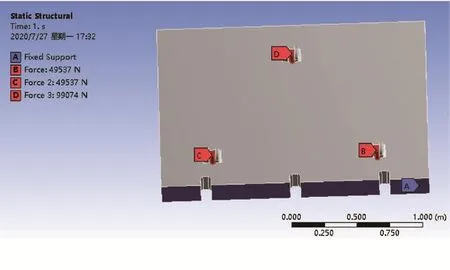
图3 推板载荷与约束图

2.2 结果分析

前处理完成后，对推板模型仿真分析求解得到推板应力应变云图，推板的变形情况如图4所示，推板的应力分布情况如图5所示。

图4 推板应变云图

由图4可以看出，推板的变形主要发生在X方向，其变形数值为3.88 mm，Y方向和Z方向的变形较小，分别为0.42 mm和0.11 mm。推板的最大变形位置集中在推板中上部，变形量的变化规律呈环状分布，由内圈向外圈逐渐降低。

由图5可得推板最大的受力区域位于推板的顶部区域，存在应力集中现象，推板下部的受力较小，所受的最大应力值为242.35 MPa，低于推板材料的屈服强度，与实际工况相符，推板结构强度符合设计要求。

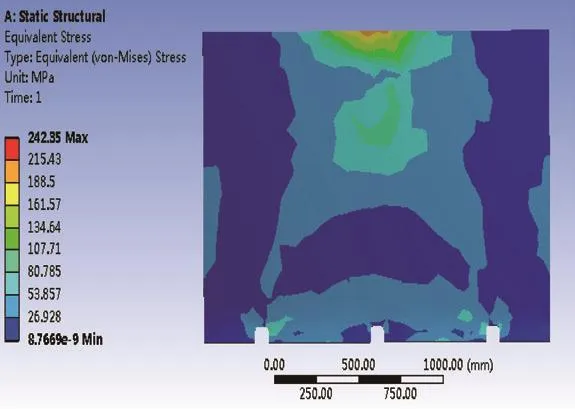
图5 推板应力云图

2.3 推板的改进

由前述推板静力学仿真结果可知，推板在X方向的变形相对较大，且最大变形位置集中在推板顶部。为保证推板的安全性，对其结构做出改进，在安装液压缸基座的一侧中上部设置加强筋。将改进后的分析模型导入Ansys Workbench中，对模型施加载荷与约束。如图6所示，在强筋A处施加固定约束，分别在液压缸基座B、C、D三处施加载荷。参照前文对推板的静力学分析步骤，完成对改进后推板的静力学分析。

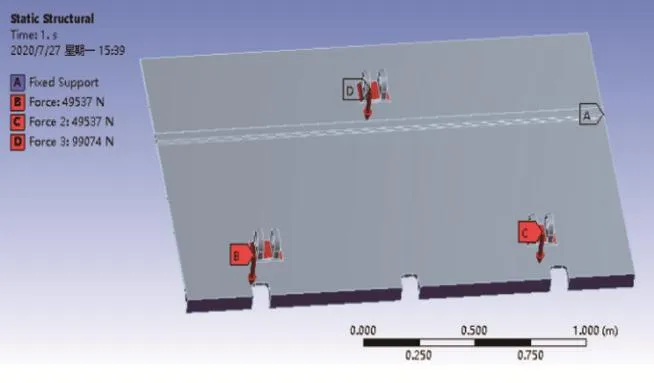
图6 改进后的推板载荷与约束图

对改进后的推板进行仿真分析所获得推板最大变形量为3.07 mm，主要变形发生在X方向，变形规律由中心向四周扩散，相比较改进前的推板变形量减少0.81 mm；改进后推板的应力主要集中在推板的中上部，最大应力为 258.38 MPa，小于设计材料的最大许用应力，故在强度上推板足够安全。

3 疲劳寿命分析

Ansys疲劳分析是基于Miner法则进行的，以推板静力学分析结果为基础，对推板进行疲劳寿命分析。根据推板应力应变情况可知，改进后的推板形变量减小。由于形变量对推板疲劳破坏影响较小，故本文重点分析推板基于高周疲劳下的疲劳寿命。

3.1 疲劳分析方法

本文基于Miner累积损伤理论应用有限寿命设计法对压缩装置的推板进行疲劳特性分析。Miner累积损伤理论描述了循环载荷对结构的持续作用，使结构发生损伤进而产生疲劳破坏。材料产生疲劳损伤的程度与应力的循环次数呈正相关，结构的疲劳损伤累积达到破坏时吸收的净功W与疲劳载荷历史无关。假定在某级应力下，材料产生破坏，其应力循环次数为N1，W表示吸收能量的极限，在经过n1次应力循环后，材料产生的疲劳损伤吸收的净功为W1，则根据Miner累积损伤理论可得

材料的疲劳累积损伤由式（3）可得

式中：ni为第i级应力水平级别下经过的应力循环次数；Ni为第i级应力水平级别下结构达到破坏时候的应力循环数。

由式（3）可知，当D的数值等于1时，评定对象开始出现破坏。

3.2 疲劳特性

在设计仿真中，疲劳分析模块需要用到在工程数据分支下的材料特性当中的S-N曲线数据。因此，在进行疲劳分析前，需对疲劳材料特性进行添加和修改，并在材料特性的工作表中插入S-N曲线。S-N曲线表示材料所受的应力幅与失效循环次数之间的关系[14],通常情况下的S-N曲线是由疲劳测试得到的，参考GB/T 3075—2008《金属材料疲劳试验轴向力控制方法》，对相关文献中应用统计学法和升降法得到的数据进行分析，将数据输入材料特性的工作列表，得到图7所示双对数曲线。

图7 双对数S-N曲线

由图7可知，在给定的应力比下，应力范围S越小，寿命越长。当应力范围S小于某极限值时，试件不发生破坏，寿命趋于无限长。

3.3 仿真设置

对疲劳工具Fatigue tool进行初始设置，在初始设置中，对疲劳载荷类型进行定义。由于推板承受的是循环载荷，故在设置中选择类型为Fully Reversed，对于交互应力循环不需考虑平均应力理论；在Fatigue Tool中添加Life、Safety Factor、Fatigue Sensitivity命令；通过Life模块，选择Evaluta all Results计算。

3.4 结果分析

推板在循环载荷作用下的疲劳寿命云图如图8所示。图中推板在循环载荷作用下的最大疲劳寿命值为9.7×106次循环，最小值为9.2×106次循环，满足设计要求。推板在循环载荷作用下的安全因子云图如图9所示。

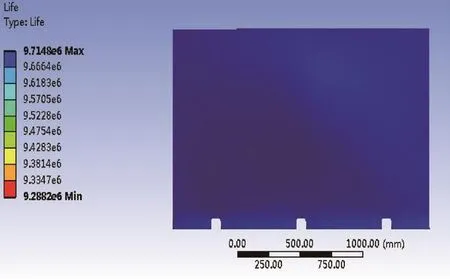
图8 疲劳寿命云图

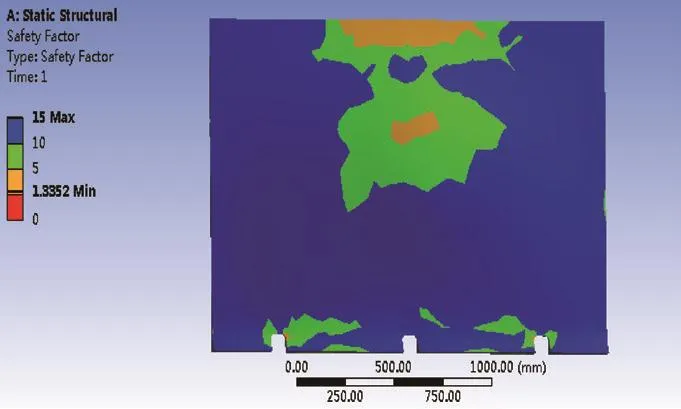
图9 安全因子云图

由图9可知，推板的最小安全因子为1.335 2大于1，最大安全因子为15，故推板整体结构较为安全。

在临界区域内，部件的寿命、损伤或安全系数等参数随载荷的变化而变化，这种变化情况通过疲劳寿命曲线图得以体现，如图10所示。

由图10可知，当最大基本载荷扩大范围为0.5～1倍时，疲劳寿命值基本保持不变；当最大基本载荷扩大1倍，疲劳寿命值骤减，下降幅度变大；当最大基本载荷扩大到1.1倍，疲劳寿命循环次数为4.1×105次。推板在循环载荷作用下的双轴指示结果如图11所示。

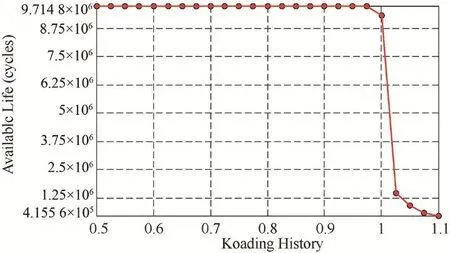
图10 疲劳寿命曲线

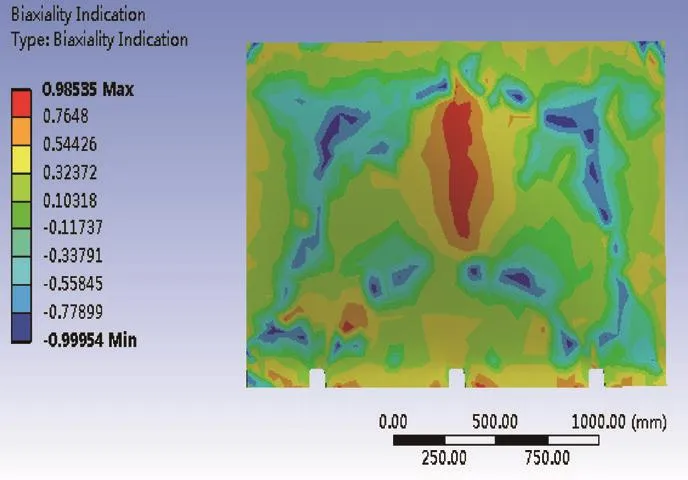
图11 双轴指示结果

由图11可知，推板所受应力值最大区域在中上部位置，集中在推板与液压缸基座焊接处，与静力学应力仿真结果相对应。因此，在对推板进行设计时，应注重与推板相连的液压缸基座处的设计，此处产生疲劳裂纹的可能性较大，疲劳裂纹会直接影响推板的疲劳寿命。

4 结论

1）静力学分析结果表明，改进前推板的变形量为3.88 mm，变形相对较大；改进后推板的最大变形量为3.07 mm，最大应力为 258.38 MPa。最大应力小于设计材料的最大许用应力，故在强度上推板是足够安全，产生的应力主要位于推板中上部。

2）疲劳寿命分析结果表明，推板在循环载荷作用下的最大疲劳寿命值为9.7×106次，最小值为9.2×106次。将最大基本载荷扩大1.1倍后，推板的疲劳寿命循环次数降为4.1×105次；与推板相连的液压缸基座处所受应力最大，产生疲劳裂纹的可能性最大；整体来看，推板结构较为安全。