“双新”背景下数学建模融入高中数学的探究

敖羚峰

［摘  要］ 随着教育理念的不断更新，以及新课改的推进，新课标、新教材、新高考越来越重视对学生数学应用意识的培养与考查，数学建模作为一种重要的数学思想与学科素养，它也变得越来越重要. 但目前中学阶段的数学建模课程建设才刚刚起步，缺乏实际案例. 中学应该如何开展数学建模活动呢？对此，研究者从课堂、活动两个方面做了思考，设计了两个案例并进行实践，最后提出了教学策略.

［关键词］ 数学建模；高中数学；案例研究

研究背景

随着新一轮课改的推进，新的课程标准发生了较大变化，其中最大的变化就是：将数学建模上升为六大核心素养之一，并将其提炼为一条单独的知识主线. 它指：将现实问题抽象为数学问题，再用数学方法构建模型，从而解决问题.

为了更好地落实数学建模素养，新教材中耗费了大量篇幅来讲述数学建模，甚至还以专栏的形式开辟建模领地. 例如人教A版必修一教材第162页，设计了一个“建立函数模型解决实际问题”专栏，要求学生结合数据，建立函数模型，计算茶水的最佳泡制时间. 再例如人教A版选择性必修三教材第141页，设计了一个“建立统计模型进行预测”专栏，要求学生结合数据，应用所学的统计模型，对城市的空气情况进行预测，提出优化方案. 这在国内教材发展史上，从来没有过.

新高考也呼应了“双新”（新课程、新教材）的要求，近几年的高考中，涌现了大量的数学建模试题. 例如2021年全国Ⅰ卷中的剪纸模型，全国Ⅱ卷中的北斗卫星导航系统模型，全国甲卷（理科）中的三角高程测量法模型；2020年全国Ⅰ卷（理科）中的埃及胡夫金字塔模型，全国Ⅱ卷（理科）中的北京天坛模型，全国Ⅲ卷（理科）中的Logistic模型；2019年全国Ⅰ卷（理科）中的断臂维纳斯模型，全国Ⅱ卷（理科）中的鹊桥模型和印信模型等. 由此可见，数学建模在新课改中，占据着越来越重要的地位.

现状分析

数学建模在教学中实施得如何呢？事实上，不太理想. 张思明教授在一次报告中谈到他们团队在全国范围内做了一次大数据调研，调研从两个方面展开. 一方面是学校与教师方面，目前各中学对数学建模的重视度不够，教师对数学建模课程的建设落实不到位，要么是课时配置不够，学生一学期只能上一到两次数学建模课程，远远达不到新课标要求的10课时的标准；要么是落实过程中有一些走样，通过其他方式替代数学建模课程. 其中最为突出的，就是将传统的解数学应用题与数学建模画上了等号，即通过传统的数学应用题的讲解与练习替代了数学建模过程. 这种处理方式，并未组织学生经历从现实情境中抽象出数学问题与模型的过程，因此学生很难体会到数学的应用价值. 另一方面是学生方面，在调研中他们发现，学生在课堂中学习课本知识的能力是很强的，这表明学生的数学思维能力并不弱. 但是，一旦接触到现实情境问题时，学生就会感觉陌生，无从下手，因为他们还不具备将现实情境与数学情境相结合的能力. 所以，加强数学建模课程的建设以及学生数学建模素养的培养是十分有必要的.

教学案例

中学阶段究竟应该如何开展建模活动呢？笔者依据自己参与建模活动与竞赛的一些经验，从两方面谈谈自己的思考.

1. 立足教材知识，建设研讨课堂

数学建模无处不在，可以说贯穿整个高中数学知识体系. 教师讲授完某个知识后，可以专门用一到两节课的时间，针对该章节知识，开展课堂研讨活动，在活动中培养学生的数学建模素养. 上海市纪雪颖老师曾开展了“菠萝中的数学”［1］课堂研讨活动，本文在此基础上丰富与完善数学建模.

案例1 菠萝中的数学.

步骤1 提出问题.

师：同学们，菠萝是我们喜欢的水果，吃菠萝前要削皮去籽儿，去籽儿的方法有很多，能否举例呢？

经过短暂思考，有学生说竖着切，有学生说一圈一圈横着切，这是最容易想到的；还有一个学生很细心，他说有的水果店是斜着切的.

师：那问题来了，为什么水果店会选择斜着切呢？难道它比其他两种方法更优秀吗？能否从数学角度进行解释呢？

步骤2 分析问题.

此时，学生的新奇感油然而生. 教师再将这个问题细致化分析如下：在去籽儿的过程中，必然会削掉一些果肉，我们当然希望削掉的果肉越少越好，因此我们关注的对象即为果肉损失量. 故原始的实际问题可以提炼为：如何去籽儿才能减少果肉损失量？

步骤3 建立模型.

有了问题，接下来就是建立模型. 教师引导学生从刚刚学习过的立体几何知识出发进行思考，很快就有学生反应到：哎，这不就是立体几何中的最短路径模型吗？为了简化问题，假定切的厚度不变，则削掉的果肉量正好与刀痕的长度成正比，长度越短，损失量也就越少，反之亦然. 此时，学生已经初步具备了建模意识.

为了进一步简化问题，教师将菠萝抽象为圆柱体（如图1所示），其中“点”代表籽儿，“线”代表刀痕. 要解决的问题，进一步转化为了学生熟悉的数学问题：怎样切，才能使线段长度最短？学生经历从生活语言过渡到文字语言的转化过程，逐步养成了数学建模素养.

步骤4 求解模型.

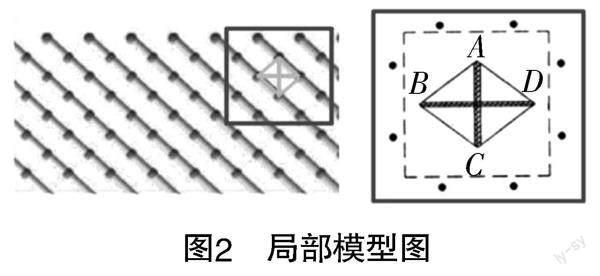
接着教师提问：怎么计算呢？学生立即想到几何体的表面展开图，将立体问题转化为平面问题. 可以看到，学生的几何基本功还是很扎实的. 教师再提问：通盘考虑比较復杂，能否对其进行简化呢？接着学生采用了“特殊化”思想，选取了图形局部进行思考，并绘制了数学图象（如图2所示）. 其中，BD代表横着切，AC代表竖着切，BC代表斜着切. 将线段总长度的计算转化为了两点之间距离的计算（两点之间距离越短，线段总长度也就越短），即比较BD，AC，BC的长度. 在这个过程中，学生应用了平面化、特殊化这两个数学思想，顺利将立体问题转化为了局部平面问题，从文字语言过渡到了图形语言，进一步发展了数学建模素养.

步骤5 回答问题.

最后，学生利用平面几何知识进行了计算，得出结论：对于常见的菠萝，斜着切是果肉损失最少的切法.

设计意图 这节课，从一个生活小实例出发，通过课堂研讨的方式，让学生经历“从生活中提出问题，再转化为数学问题，接着建立数学模型，然后求解模型，最后解决问题”的过程. 在整个过程中，学生直观感受到了生活中处处有数学，体会到了数学的应用价值，培养了数学建模素养.

2. 取材校园环境，建设实践课堂

数学建模不仅存在于课本之中，还大量存在于课堂之外. 在学生学习生活的校园中，处处有数学建模身影. 建筑物的高度、消防演习疏散方案、运动会3000米的跑法，都可以成为数学建模素材.

案例2 应用所学知识，测量名人塑像的高度.

由于学生第一次正式接触数学建模，因此笔者选了一个容易操作的模型，给学生布置了一个课题：测量学校名人塑像的高度. 学生实践后撰写了相应报告，下面选取其中两份，对其进行分析.

（1）应用三角知识，构建相似模型.

学生小齐利用的是三角形几何学知识，实践测量后撰写报告，探究过程共六个步骤.

步骤1 构建模型.

小齐利用人高构建了相似三角形模型：找准一个A点，使得A点与人的头顶（即点E）、名人塑像的头顶（即点C）在同一直线上，再利用△AEF与△ACD相似计算出名人塑像的高度.

步骤2 采集数据.

小齐在理论分析框架的基础上，到实地采集数据. 但采集数据时，小齐遇到了困難：如何准确找到A点呢？经过思考，小齐想到了相机定位的方式，逆向寻找A点的位置：先粗略估计A点的位置，再通过相机拍摄，在一定角度下，移动相机的位置，当相机中人的头顶与名人塑像的头顶恰好重合时，即可视为三点共线. 这个方法相当优秀，充分展现了学生的创新能力.

找到A点后，接着需要测量AF的长度，但是小齐手上没有米尺可以使用，怎么办呢？经过思考，小齐想到了人体测量法，即利用手臂与脚步来估测长度，多次测量后，得到AF=28×7=196（cm）.

测量DF的长度时，小齐又遇到了阻碍. 由于名人塑像位于一座平台上，人体测量法只能到达G点，无法得到DG的长度. 但小齐细心地发现，该平台有地砖，数一下砖块的数量，再乘上单个砖块的长度，便可以得到DG的长度. 最终，小齐测量得到DF=836 cm.

步骤3 计算模型.

小齐计算得到tan∠CAD=0.89，故CD=tan∠CAD×AD=918.48 cm. （如图4所示）

步骤4 分析误差.

这个结果与实际高度950 cm相差31.52 cm，有一定的差距，但差距不是很大. 误差主要源于以下两方面：①角度的测量. 逆推A点时，只是通过相机粗略估计，不能保证三点（A，E，C）共线，会有一定的偏差. ②距离的测量. 测量AF与DF的长度时，使用的是人体测量法，在行走的过程中，不能保证走的完全是直线，可能会有一定的偏离，产生一定的偏差.

步骤5 改进方案.

从误差分析来看，后续可做如下改进：①角度的测量：使用激光筒来确定A点的位置，可使数据更加准确. ②距离的测量：使用标准米尺进行测量，并且多测量几次，然后取平均值.

步骤6 心得体会.

实践后，学生感悟如下：①数学存在于我们的日常生活中，因此我们的数学学习要与实际生活联系起来. ②起初觉得这个任务挺简单，所以本次测量活动的准备不够充分. 但在实际操作过程中发现，原来会有很多意想不到的事情发生，以后一定要提前做好充足准备.

（2）应用物理知识，构建竖直上抛模型.

除了上述几何方法外，还有一位学生小李采用的是物理学方法.

步骤1 构建模型.

小李从物理学的角度构建了竖直上抛模型：由一人拿着小球从身前向上抛出，抛至名人塑像头部上方（在同一水平面上，A点与塑像顶部同高，M点高于A点），再由另一人记录小球抛出后第一次到达A点的时间和抛至顶点M的时间，然后运用竖直上抛模型进行计算.

步骤2 采集数据.

小李兴致勃勃地购买了弹力小球，并到实地开展实验. 但在实践过程中发现，第一次到达A点的时间与抛至M点的时间十分接近，很难同时记录.  为了保证观测数据更加接近真实值，小李坐在地面上向上抛出弹力小球.

步骤3 计算数据.

利用采集到的数据，计算得到h=9.28 m.

步骤4 分析误差.

上述数据与真实数据之间存在一定差距，该差距主要来自以下几方面：①重力加速度的值. 本实验采用的重力加速度g=9.8 m/s2，与实际数据有一定差距. ②忽略了空气阻力的影响. ③人工操作存在误差. 本实验为纯人工操作，无法保证每次抛出的点一致，而且由于身高，抛出点与落地点不可能在同一水平面上. ④人工测量存在误差. 每次实验的时间数据由人工观测与记录，实验数据会受到人工影响.

步骤5 改进方案.

从误差分析来看，后续可以做如下改进：①查阅真实的重力加速度，让实验数据更加精确. ②多人测量：单人测量会受到单人观测习惯的影响，多人同时进行观察，求取平均值，可使获得的数据更接近真实值.

步骤6 心得体会.

实践后，学生感悟如下：①感受到了所学知识在生活中的运用和学科之间的相互融合，体会到了数学的魅力. ②学到了数学建模过程和基本思路. ③由衷地感谢教师的指导和帮助，正是因为教师对教学有独特体会和创新，学生才有了开展此次活动的机会，并有希望在今后的教学活动中加以推广.

（3）案例分析.

通过本次实践活动，让学生“做中学”，体会数学建模的实践过程，渗透数学建模素养. 从上述两份案例中，我们认识到，学生具备以下素质：

严谨的科研态度. 纵观整个数学建模过程，对方案的设计，学生经历了多次修改与调整. 为了获得真实、准确的数据，学生到实地并开展了多轮实验，通过求平均值的方式减小误差. 撰写报告时，学生查阅了相关文献，按照标准格式进行撰写. 在整个活动过程中，学生都秉承严谨的科研态度.

灵敏的数学思维. 两位學生在实践过程中，都遇到了意外：学生小齐发现未携带米尺等测量工具，而且无法达到塑像底座，所以转而采用了人体测量法；学生小李发现无法同时记录预想的时间点，于是转化为记录小球的落地时间. 可以看到，学生的思维很灵活，没有因为无法完成测量而放弃，而是思考替代方案. 这正是开展数学建模实践活动的意义所在.

较强的实践能力. 实践方案由学生自主设计，实验由学生到实地开展，数据由学生采用多种方案后采集. 由此展现了学生较强的实践能力.

由此可见，学生的能力超乎我们的想象，给学生一个机会，学生将展示无穷的潜力. 因此，在中学阶段开展数学建模活动具有可行性，也相当有必要.

数学建模融入高中课程的思考

除了上述两种方式外，数学建模还可以什么方式融入高中课程呢？笔者认为可从以下几个方面进行.

（1）举办校园数学建模竞赛. 高校之间开展了较为丰富的数学建模竞赛，例如“全国大学生数学建模竞赛”“美国大学生数学建模竞赛”“‘认证杯数学建模挑战赛”等. 竞赛以现实题材为背景，设计两三道试题要求参赛学生三人一组，通过设计模型、编写程序、运行程序、生成数据、获得结果、形成论文等步骤，参与竞赛活动. 教研组可以借鉴这种模式，围绕中学数学知识，开展建模活动. 例如学习函数知识后，可以“探究茶水泡制的最佳时间”为题设计数学建模活动；学习排列组合知识后，可以“怎样包装小包纸巾最省材料”为题设计数学建模活动. 类似的案例还有很多. 学生报名参加活动，组队设计方案，撰写提交论文，最后由教研组评审，再给优秀队伍颁奖，以此鼓励学生积极参与.

（2）开设数学建模选修课. 除了竞赛外，还可以开展数学建模选修课. 选修课的开展方式可以分为三种：①呈现理论知识与案例. 由授课教师主讲，传授数学建模的相关理论知识，以及论文撰写方法，并以具体案例的方式呈现建模方案. ②课堂研讨. 给出一些实际问题，如“探究A、B系列复印纸大小之间的关系”“教学中使用的粉笔采用哪种形状更好”“购置新房，选取哪种贷款方式更合算”［2］，等等. 围绕这些实际问题，分小组运用所学知识，开展研讨活动. ③实践活动. 提供实际问题，如“如何描述中学生的投篮水平和发展潜力”. 组织学生利用网络资源、图书资源等，设计描述模型，并通过实地采集数据、生成论文报告、课堂交流分享等步骤，培养学生的建模素养.

结语

数学建模对培养学生的应用能力、开发学生的数学潜力、发展数学的学科价值具有十分重要的作用. 但目前数学建模融入高中课程的案例较少，因此需要一线教师积极探索，结合所在学校的实际情况，开展相关研究.

参考文献：

［1］ 纪雪颖. 考察“菠萝中的数学”，培育学生数学建模能力［J］. 数学教学通讯，2008（05）：26-28.

［2］ 赖嘉辉. 数学建模融入高中数学教学的案例［J］. 中学数学研究（华南师范大学版），2020（14）：14-16.