函数对称性、周期性图象变换的探究*

福建省莆田第六中学 (351111) 陈瑞清

函数的对称性、周期性是函数的重要性质,也是高考的高频考点,并且对称性、周期性的图象变形更是学生学习的难点,本文从函数解析特征为出发点进行探究总结,以期把握本质规律、促进知识融会贯通.

一、中心对称

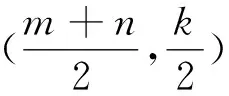
典例1 若函数f(x)对任意x∈R,都有f(1+x)+f(3-x)=2,函数g(x)=2x+f(x)在R上有最大值M与最小值m,则M+m=( ).

A．-10 B．10 C．-5 D．5

解：∵f(1+x)+f(3-x)=2,∴f(x)关于(2,1)中心对称,∴y=f(x+2)-1是奇函数,∵g(x)=2x+f(x),∴y=g(x+2)=2(x+2)+f(x+2)=2x+f(x+2)+4=[2x+f(x+2)-1]+5,∵y=2x+f(x+2)-1是奇函数,∴y=g(x+2)关于(0,5)中心对称,∴g(x+2)max+g(x+2)min=10,又g(x+2)max=g(x)max=M,g(x+2)min=g(x)min=m,∴M+m=10m,故选B.

二、轴对称

典例2 已知函数f(x)的定义域为(-∞,3)∪(3,+∞),对∀x>-1,都有f(4+x)-f(2-x)=2,当x>3时,f(x)=|log2(x-3)|,若f(x)-k≥0恒成立,求k的取值范围.

解：∵函数f(x)的定义域为(-∞,3)∪(3,+∞),又∀x>-1,都有f(4+x)-f(2-x)=2,∴当<3时,则6-x>3,f(x)=f(6-x)-2=|log2(3-x)|-2,∴x<3的函数图象是由x>3的图象先作轴对称后,再向下平移2个单位得到的(如图1).∴当x=2时,f(x)min=-2,f(x)-k≥0恒成立⟺k≤f(x)min=-2,∴k≤-2.

图1

图2

三、周期性

函数f(x)在定义域内对任意的x,都有f(m+x)-f(x+n)=0(m、n为常数),其自变量m+x与n+x差为定值m-n,函数值差为定值0,则f(x)是周期函数,周期T=|m-n|.

引申3 若f(x)在定义域内对任意的x,满足f(m+x)-f(x+n)=k,(m、n、k是常数,k≠0),则函数f(x)的图象显周期性上下平移变换,周期T=|m-n|.

引申4 若f(x)在定义域内对任意的x,满足f(m+x)-tf(x+n)=0,(m、n、t是常数,且t≠0),则函数f(x)的图象显周期性纵向伸缩变换,周期T=|m-n|.

图3

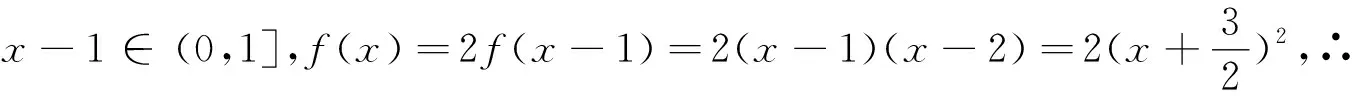
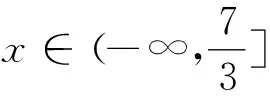
引申5 若f(x)在定义域内对任意的x,满足f(m+x)+f(x+n)=0(m、n是常数),则f(x)是周期函数,周期T=2|m-n|.

典例6 已知f(x)在R上是奇函数,且f(x+2)+f(x)=0,当x∈(0,2)时,f(x)=2x2,则f(7)=( ).

A．-2 B．2 C．-98 D．98

解：∵f(x+2)+f(x)=0,∴f(x)是以4为周期的周期函数,又f(x)为奇函数,∴f(7)=f(7-4×2)=f(-1)=-f(1),而f(1)=2,即f(7)=-2.故选A．