例析平移坐标系法求解函数问题
浙江省杭州第十四中学 (310006) 楼思远
文[1]研究了平移坐标系法在圆锥曲线中的应用,实际上,平移坐标系法对处理部分函数问题也有立竿见影的效果.我们知道,在平面内对直角坐标系任意进行平移后,函数图象的形状、直线的斜率、线段的长度,多边形的面积等均保持不变,特别的,只对直角坐标系左右平移时,函数的零点个数也保持不变,我们把这些不变的量统称为“运动不变量”,基于这些不变量以及函数本身的性质,通过适当的平移坐标系来对解题思路作出调整,可起到化繁为简的效果,并揭示出问题的本质.
一、实例分析
例1 若对任意的a,b∈R,不等式|x2+ax+b|≤1在区间[m,n]上恒成立,则n-m的最大值为________.
分析:原函数含有两个参数,比较复杂,现将直角坐标系平移使得原点O与二次函数y=x2+ax+b的顶点重合,则二次函数解析式变为y=x2,如图1所示,注意到平移过程中函数的形状保持不变,因此可以将原问题转化为在图1的基础上求解.
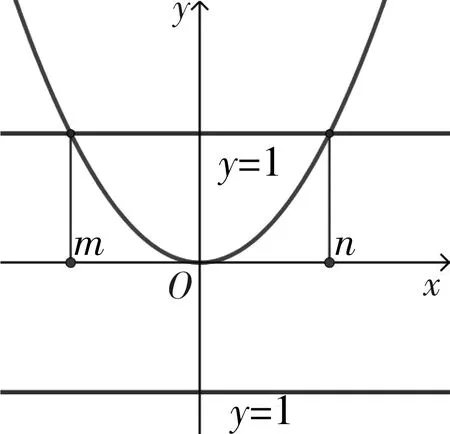
图1
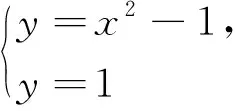
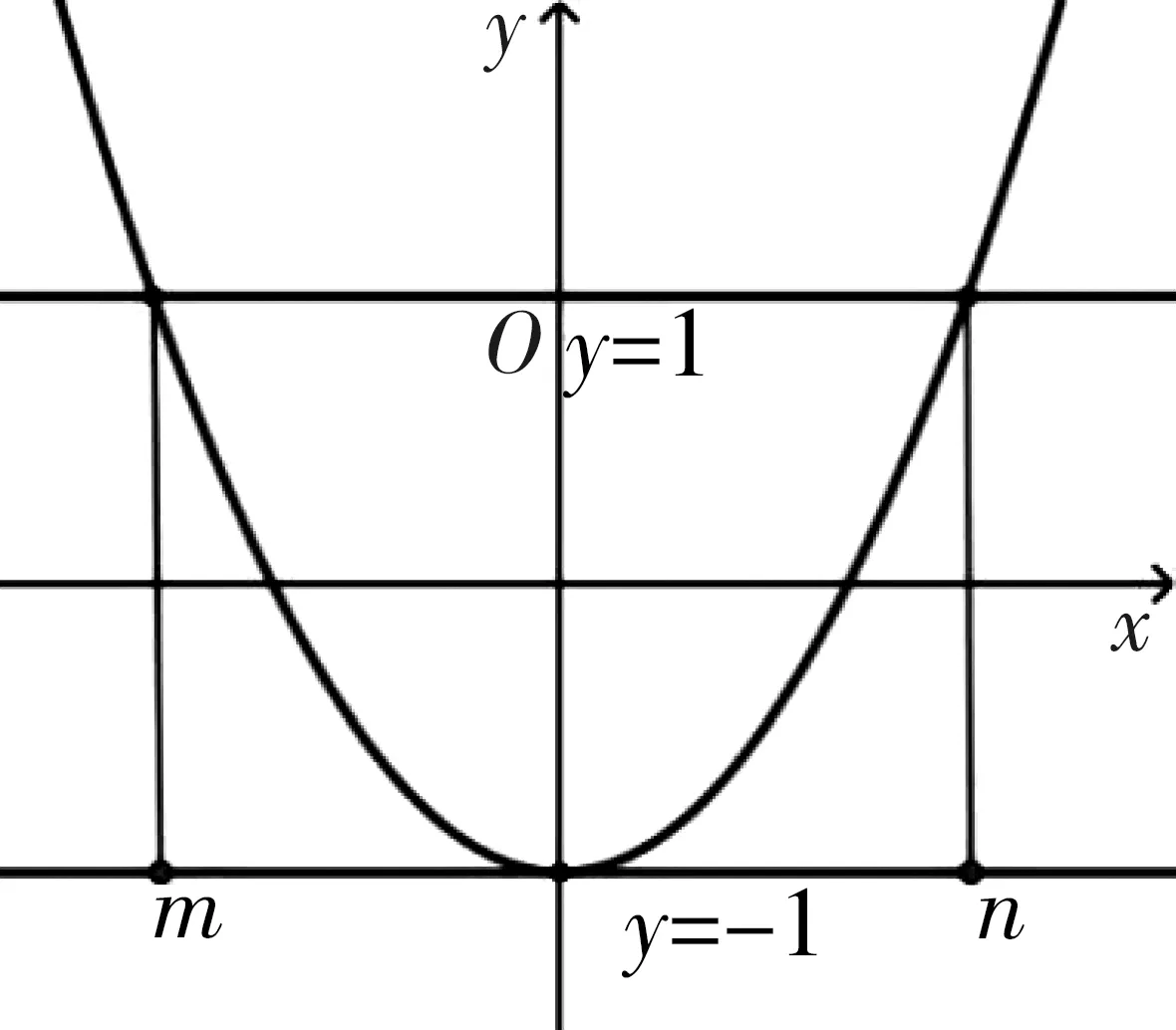
图2
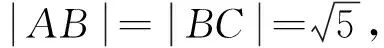
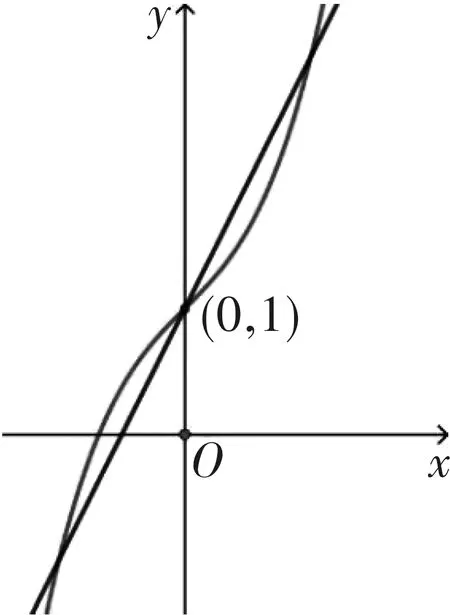
图3
分析:在图3中,函数过点(0,1),现将直角坐标系往上平移使得原点O与(0,1)重合,如图4所示,此时函数解析式变为y=x3+x,是一个奇函数,由于平移过程中直线l的斜率与线段AB与BC的长度均保持不变,故根据对称性知点B必然与原点O重合,在这种情况下,利用奇函数的性质可对问题快速求解.
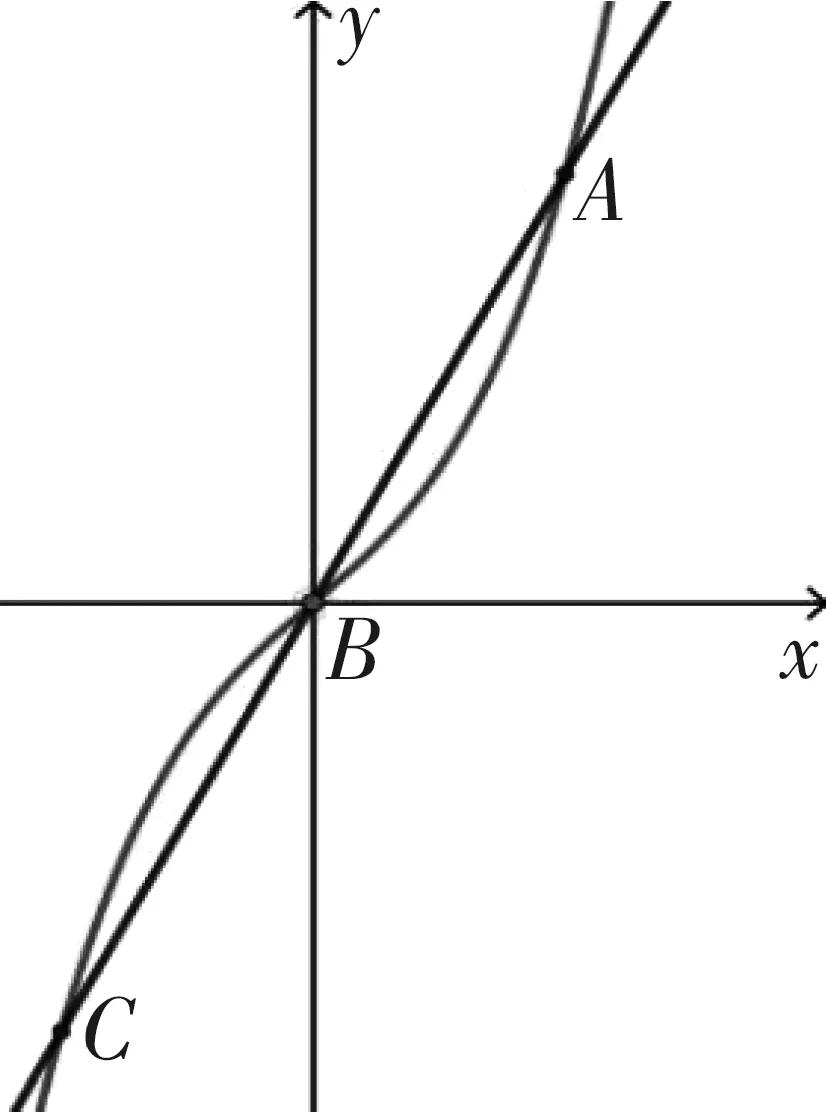
图4
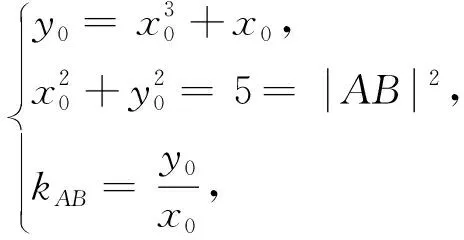
例3 如图5所示,已知A,B,C,D为三次函数y=x3+ax2+bx+c图象上不同的四点,A,C为两个极值点且CD//AB,若A,B,C,D四点构成一个菱形,试求SABCD的值.
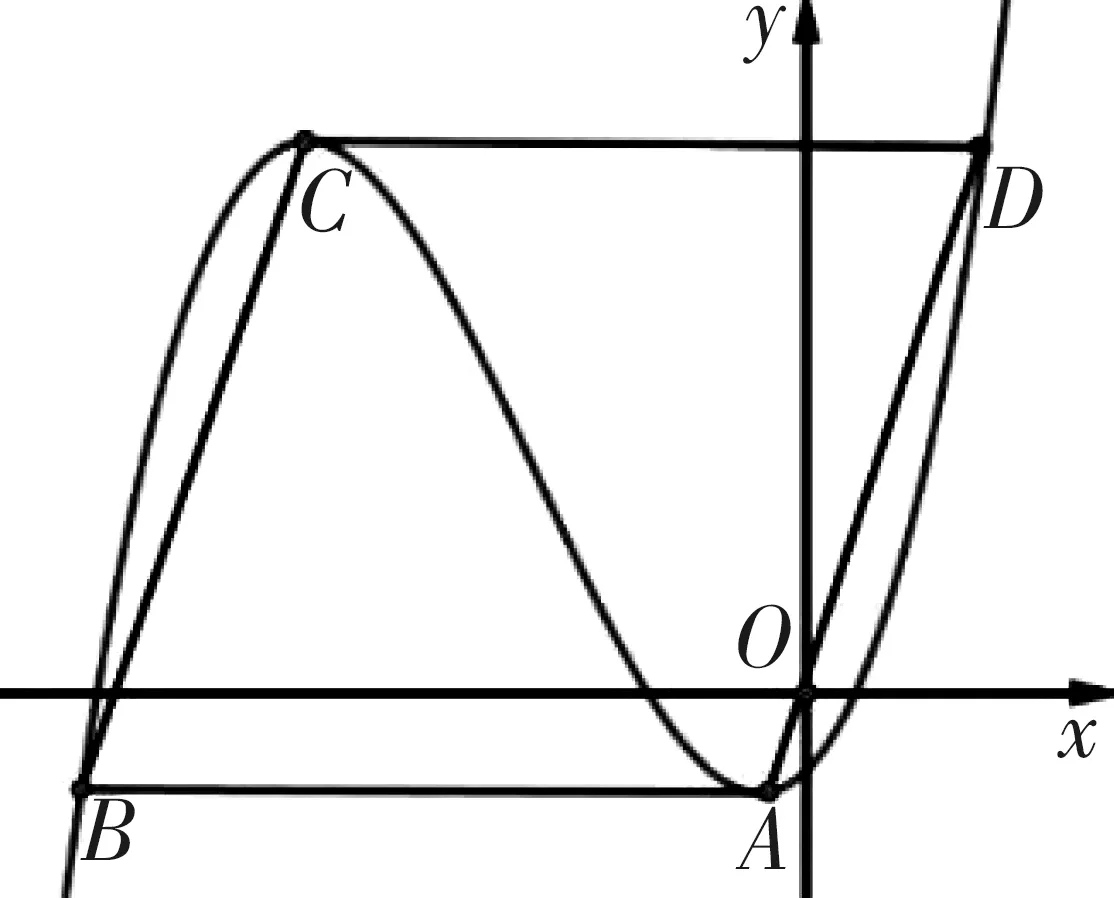
图5
分析:原函数含有三个参数,比较复杂,现将直角坐标系平移使得原点O与点C重合,如图6所示,根据零点位置可设三次函数解析式为y=(x-0)2(x-t),注意到平移过程中函数的形状与SABCD面积大小均保持不变,因此可以在图6情形下求解.
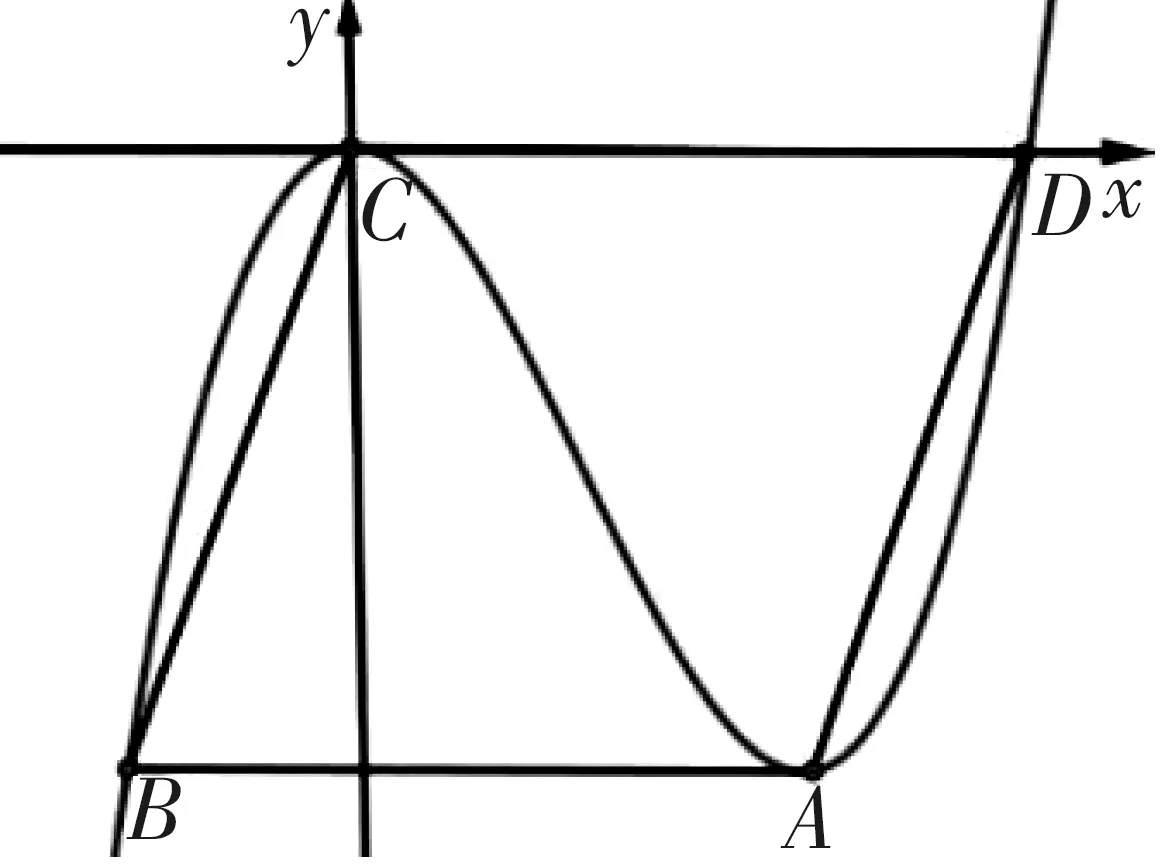
图6
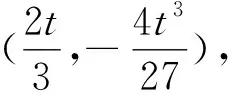
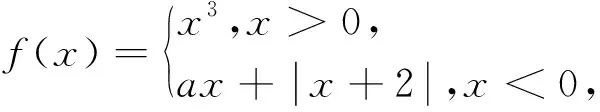
分析:将函数图象左右平移不改变函数零点的个数,通过观察和尝试,发现将直角坐标系向右平移一个单位,可以使函数y=f(x-1)+f(1-x)变为y=f(x)+f(-x),为一个偶函数,根据对称性,题目等价于y=f(x)+f(-x)=0当x>0时有两个解.
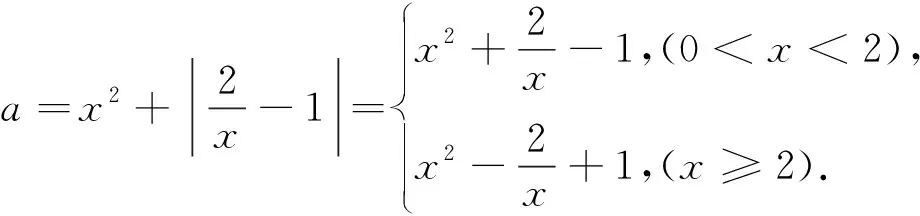
通过求导求得到函数的极值,并作出大致图象如图7所示,易知a>2时有两个交点.故实数a的取值范围是a>2.
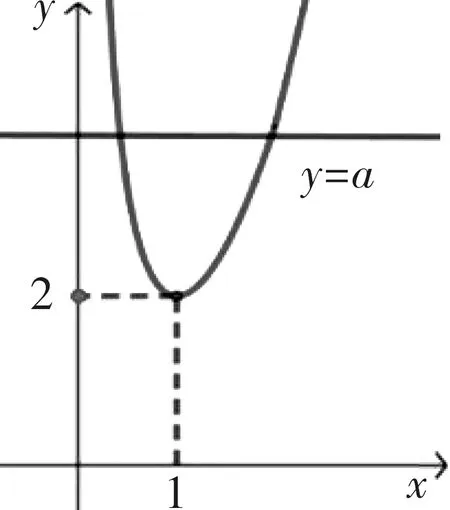
图7
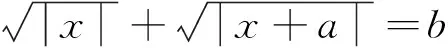
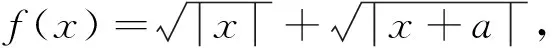
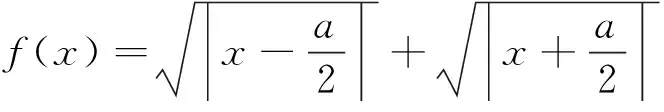
二.几点思考
对上述几个问题而言,直接求解将十分繁琐,作为对照,通过平移坐标系这一操作,可以直指问题的本质,以简驭繁快速解答.这其中,结合题意进行观察与尝试,发现并抽象出“运动不变量”是解题思路(平移直角坐标系)的关键,因此,数学抽象能力是根本所在.文[2]指出:“数学抽象是数学核心素养的重要构成内容,在新的教学改革中,数学抽象位于核心素养首位,意在通过对学生抽象素养的培养引导学生利用推理、运算、建模等数学活动方式揭示世界中蕴含的数学规律”.在平时的教学过程中,教师应重视学生抽象思维能力的培养,及时调整教学手段和教学方法,从情境与问题、知识与技能、思维与表达等维度开展数学抽象能力培养的教学,另外,可以引导学生结合直观想象与数据分析等思维方式,从相似问题中抽象出一般性的数学规律与解题技巧.
本文仅就平面直角坐标系的平移展开了讨论.实际上,从横向角度而言,对空间直角坐标系进行平移,可以简化立体几何问题的坐标运算;从纵向角度而言,除了平移外,对直角坐标系进行旋转与伸缩等变换,可以解决其各种类型的问题,例如通过旋转坐标系可以将等轴双曲线转化为反比例函数的图象,从而简化运算过程,等等,此类问题待读者进一步研究.

