夯实基础强本质,彰显能力重创新*
——基于“三新”背景下的三角函数大单元的深度学习
陕西省安康市汉阴中学 (725100) 梁 华
在新教材(人民教育出版社2019年国家教材委员会专家委员会审核通过)、新课程(《普通高中数学课程标准(2017年版,2020年修订》)、新高考的“三新”背景下,三角函数模块知识试题的命题具有明显的特点,更注重数学知识的基础性、网络性,夯实基础;凸显数学知识的综合性、联系性,强化本质;展示数学思维的灵活性、应用性,彰显能力;强调数学意识的探究性、创新性,侧重创新等,更强调结合三角函数自身以及三角函数与其他知识之间的联系,充分体现高考数学的考查效能、选拔功能及高考的区分功能.
1.夯实基础,构建网络
“三新”背景下三角函数的命题,突出对三角函数的概念与定义、图象与性质、基本公式等层面的考查,全面构建三角函数的知识网络,注重三角函数的基础知识的理解与掌握,全面夯实基础.

A.ω=2 B.f(x)的值域是[-2,2]

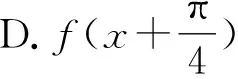
分析:根据题设条件,通过函数f(x)的周期满足的不等式以及对称中心,构建相关参数的不等式或关系式,得以确定对应的参数值,进而确定三角函数的解析式,利用三角函数的图象与基本性质来分析与判断.

综上,本题选择A、C.
点评:三角函数的图象与基本性质是解决相关三角函数问题中的基础所在,也是高考三角函数模块中的根本.解决此类问题的关键就是利用题设条件确定对应的参数值,正确构建对应的三角函数解析式,为进一步的综合与应用提供条件.
2.强化本质,增加联系
“三新”背景下三角函数的命题,强化三角函数的本质属性与内涵,注重三角函数与函数、三角函数与解三角形以及三角函数与其他知识之间的联系,突出三角函数的自身应用以及其与其他知识的联系,展示内涵本质.
例2 (2023届台州市高三数学一模题)设△ABC的三个内角A,B,C所对的边分别为a,b,c.若A≠B,且sinAcos(2B-A)=sinBcos(2A-B).则tanAtanB的值为________.
分析:根据题设条件,结合解三角形与三角函数的联系,借助题设中的三角关系式,寻找关键角A-B进行整体思维,利用三角关系式合理配凑与巧妙转化,结合三角恒等变换公式进行转化与求解.

点评:三角函数与解三角形之间的综合与联系,是三角函数模块知识中比较常见的一种联系方式.此类问题中,关键是寻找角与角之间的关系,或单独处理,或整体思维,特别是利用关键角的整体应用,往往是合理配凑与整体思维的巧妙应用,对于解决此类三角函数关系式具有很强的应用性、技巧性.
3.彰显能力,凸显思维
“三新”背景下三角函数的命题,熟练理解并掌握三角函数中的相关概念与公式,重视三角公式的应用,开拓三角函数的考查空间与思维角度,提升相应的认知水平与解题技巧,提升数学能力,凸显数学思维.
例3 (2022—2023学年南京市高三(上)学情调研数学试题)已知函数f(x),任意x,y∈R,满足f(x+y)f(x-y)=f2(x)-f2(y),且f(1)=2,f(2)=0,则f(1)+f(2)+…+f(90)=( ).
A.-2 B.0 C.2 D.4
分析:结合已知条件f(x+y)f(x-y)=f2(x)-f2(y)的结构特征,合理联想到三角函数模型的正弦平方差公式sin2x-sin2y=sin(x+y)sin(x-y),合理配凑系数,构建特殊三角函数模型来进行特殊化处理.

点评:借助三角函数模型来特殊化解决此类问题时,往往是结合抽象函数的结构特征与对应的三角函数公式加以联系,其中三角函数模型f(x)=Asinωx(A,ω≠0)或f(x)=Acosωx(A,ω≠0)中的最值情况由系数A决定,周期情况由系数ω决定,根据具体场景加以合理正确选取.
4.侧重创新,强调意识
“三新”背景下三角函数的命题,结合三角函数与基本知识的交汇融合、三角函数的实际应用问题以及三角函数中的数学文化等问题的创设,合理创新与应用,有效增强数学思维与能力的综合性、创新性,展示三角函数的创新应用,强调创新意识.

A.15π B.12π C.6π D.3π
分析:通过创新场景的类比,利用干支纪年历法的规律,类比确定“加(减)”混合类的三角函数的最小正周期的求解,结合正弦型(或余弦型)函数的最小正周期的确定,并结合最小公倍数的确定来综合与应用.

点评:在创新场景下,通过类比思维与类比创新,构建不同知识之间的链接,通过合理的推理与证明,实现数学文化知识与三角函数知识之间的关联,形成数学思维的创新性、数学方法的创新性等.
在“三新”(新教材、新课程、新高考)背景下,进一步落实“双减”政策与新改革理念,积极贯彻《总体方案》要求,高考三角函数知识模块的命题特色在寻求基础、本质、能力、创新等的基础上,更多侧重数学基础与关键能力的考查,坚持开放创新与核心素养导向,更加注重数学创新意识与创新应用,全面体现高考的选拔性与区分度.

