高中数学教材与课程标准的一致性分析
刘一冬 李逸芸 杨作东


摘 要:通过SEC一致性分析方法,人教A版教材(2019年版)和蘇教版教材(2020年版)必修一“不等式”部分与2017年版课程标准总体上一致性显著.在认知水平上,两版教材与课程标准之间仍存在一定差异,在理解水平和探究水平的侧重高于课程标准,在识记水平和应用水平的侧重低于课程标准.建议教师整合题目资源,充分利用习题素材;建议教材编写者重视高水平认知,及时更新习题配置.
关键词:高中数学教材;课程标准;一致性分析
课程标准为课程实施提供指导方向,教材是数学课程实施的重要物化载体.美国研究者采用SEC一致性分析工具对数学教材与“课程标准”的一致性分析做了全面系统的调查实践,经过了基础测评(检测一致性程度)、系统深化(检测不一致程度)和模式改进(简化分析模式)三个层次阶段,研发了评估和改进基础教育教科书质量的一致性分析模式[1].目前我国中学数学的一致性研究总体上处于借鉴国外经验的阶段,主要集中在评价学业考试与课程标准的一致性,并有学者尝试基于数学学科核心素养对一致性分析框架做本土化改进;也有少数学者对教师和学生认知的一致性进行了研究;而关于高中教材与课程标准的一致性研究相对较少.2017年我国教育部对高中数学课程标准进行了修订,因此考查新课标思想理念在新教材中的落实程度以及如何考查显得愈加重要.“不等式”在此次修订中被调整为预备内容,笔者尝试采用SEC一致性分析方法,就不等式内容对人教A版和苏教版教材与《普通高中数学课程标准(2017年版)》(以下简称为课程标准)的一致性进行研究,并根据SEC模式的局限补充针对性分析.期望为评价课程实施和推动一致性模式本土化提供一定的参考,为教师教学和教材编写提供一定的启示.
1 研究方法与工具
一致性分析模式是指判断、分析课程系统各个要素之间吻合程度的理念、程序与方法的总和[1].Webb模式、SEC模式和Achieve模式是目前一致性分析的三大主流模式.SEC(Surveys of Enacted Curriculum——课程实施调查)模式由Porter,Smithson等人提出,本质上是一种内容分析法,相较于另外两种模式,SEC一致性分析的灵活性与实用性较强,能够对一致性进行整体性判断,能够广泛应用于评价课堂教学、学业考试、教材与课程标准的一致性程度.在对教材的研究中,SEC一致性分析从内容主题和认知水平两个维度入手,统计不同主题下不同认知水平的内容数,据此计算Porter一致性指数(Porter,2002)[3],再根据临界值(Gavin,2011)[4]来判断一致性程度.为了提高编码工作效率,提升一致性工具的可行性与使用性,Morgan等人对八种简化方法进行比较,发现与教科书整体的一致性系数最为接近的三种简化方法是“教科书的主要部分”“仅问题”和“每5个问题”[1].由于例题习题也是我国教材的重要组成部分,本文采用“仅问题”的简化方法,研究“不等式”例题习题与课程标准的一致性.
具体操作步骤如下:
(1) 构建内容主题×认知水平二维矩阵.确定内容主题和认知水平,分别划分为t个主题和k个水平,并对其内涵进行界定.
(2) 编码与统计.对课程标准的内容和教材的例题习题进行编码,统计不同主题下不同认知水平的内容数,得到t×k频数矩阵.
(3) 计算一致性系数.先对频数矩阵进行标准化处理,再运用Porter一致性计算公式得到一致性系数P. Porter一致性公式如下:
其中aij和bij分别是课程标准和教材频数矩阵标准化后的对应元素.
(4) 确定双侧临界值,判断一致性程度.首先将s项课程标准内容和r项教材内容(例题习题总数)分别随机分配到t×k矩阵中,对两个矩阵分别标准化处理得到P.将这个随机模拟过程重复20000次,得到一致性系数分布.依据中心极限定理,P近似服从于正态分布.对其进行双侧检验(α=0.05)得到双侧临界值,从而判断(3)中所求一致性系数P是否在统计意义上显著.若一致性系数小于下侧临界值,则认为不一致;若落在两临界值之间,则认为具有一致性,但一致性程度不显著;若一致性系数大于上侧临界值,则认为一致性程度显著.
本文利用MATLAB和SPSS软件进行数据处理,对人教A版和苏教版教材“不等式”例题与习题进行一致性分析.
2 研究过程
2.1 概念界定
不同学者对一致性涵义的解读不同,但共同点在于描述一个系统中不同要素之间的匹配与吻合程度.本文将一致性界定为教材例题习题与课程标准的匹配程度.
2.2 维度划分与编码统计
首先确定内容主题.根据课程标准必修“不等式”部分的内容要求,内容主题维度划分为“等式与不等式的性质”“基本不等式”“从函数观点看一元二次方程”和“从函数观点看一元二次不等式”四个部分(分别记为T1,T2,T3,T4).
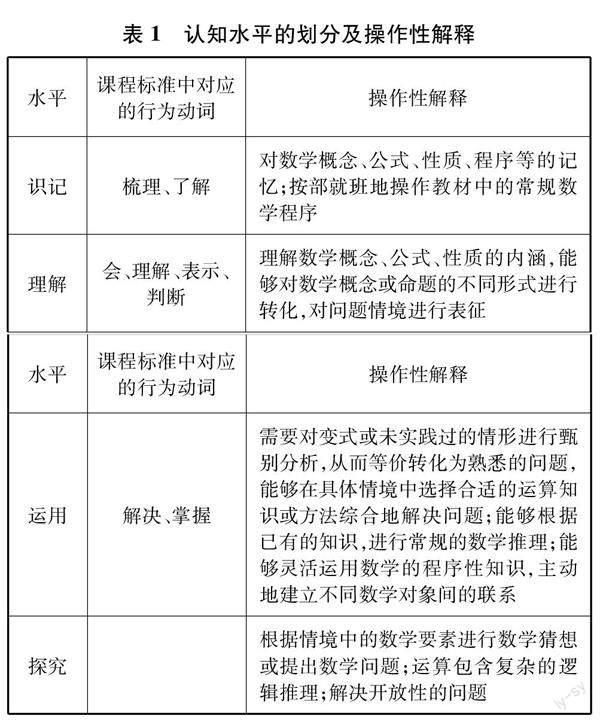
其次确定认知水平.我国课程标准中含有结果目标和过程目标,本文着眼于考查例题习题与课程标准的一致性,因此仅对课程标准中结果目标的认知层次进行划分.参考青浦实验以及李淑文等人的划分对认知水平进行界定[5],分为“识记”“理解”“应用”和“探究”四个层次(分别记为K1,K2,K3,K4).
编码以小题为单位,记录其所属的内容主题和认知水平.题目编码举例如下:
例1 计算下列两个数的算数平均数与几何平均数(其中p>0)
(1) 2,8;(2) 3,12;(3) p,9p;(4) 2,2p2.
确定其内容主题,该题属于“基本不等式”(T2).确定其认知水平,该题目需要按照算数平均数和几何平均数的定义计算即可.因此认知水平上属于识记水平(K1).
例2 已知不等式ax2+bx-1>0的解集是{x|3<x<4},求实数a,b的值.
确定其内容主题,该题属于“从函数观点看一元二次不等式”(K4).确定其认知水平,解题需要联系一元二次不等式、一元二次方程和二次函数之间的关系,得到a>0,且3和4是对应一元二次方程的根,联立方程可求得a,b.因此属于理解水平(K2).
对课程标准和人教版、苏教版两版教材的内容数量进行统计,课程标准具体要求统计内容共9项,人教版教材统计内容共109项,苏教版教材统计内容共164项.两位硕士生各自独立编码,再对有分歧的题目进行讨论.判断编码一致性,Cohens Kappa系数为0.718(p=0.000<0.05),表明编码一致性较强.取两位编码者的内容数统计的平均数作为统计结果.
3 两版教材与课程标准一致性分析
3.1 总体情况分析
人教版教材例题习题与课程标准的一致性系数为0.6121,高于上侧临界值0.4407;苏教版教材例题习题与课程标准的一致性系数为0.6081,高于上侧临界值0.4412.两版教材“不等式”的例题习题与课程标准的一致性显著.
3.2 局部情况分析
为了更直观地呈现两版教材“不等式”例题习题与课程标准的一致性情况,将教材数据统计矩阵(标准化后)与课程标准数据统计矩阵(标准化后)做差,并做出如图1所示的等值线图.
由上图可知,两版教材例题习题与课程标准发生偏离的分布大致相似,偏离以正偏离为主,在不同内容主题下对于认知水平的要求侧重不同.
在内容主题维度,两版教材的正偏离主要集中在“等式和不等式的性质”(T1)、“基本不等式”(T2)和“从函数观点看一元二次不等式”(T4),负偏离主要集中在“从函数观点看一元二次方程”(T3).在人教版“不等式性质”部分,理解水平的题目占了不少比例,因此图中(T1,K2)会出现较大的正偏离;两版教材识记水平的题目几乎没有,因此(T1,K1)出现一定的负偏离.人教版“从函数观点看一元二次方程”的例题和习题设置较少,因此T3会出现较大的负偏离;而苏教版在这一方面更贴近课程标准.人教版和苏教版对“从函数观点看一元二次不等式”部分都设置了相当多的纯计算题,因此两版教材的T4都出现较大的正偏离.
在认知水平维度,两版教材的正偏离主要集中在“理解水平”(K2)和“运用水平”(K3),其中正偏离较大的区域是(T2,K1)、(T2,K2)和(T4,K3).此外,人教版的(T1,K2)和(T4,K1)也出现了较大的正偏离.人教版的较大负偏离主要集中在(T1,K1)、(T2,K3)和(T3,K2),苏教版的较大负偏离重要集中在(T1,K1)、(T2,K3)和(T3,K1).两版教材对于“基本不等式”和“从函数观点看一元二次方程”的认知侧重不均衡.
为了具体地显示两版教材不等式例题习题在内容主题和认知水平上的差异,作权重柱状图如图2所示.在内容主题上,两版教材在“基本不等式”和“从函数观点看一元二次不等式”部分的权重都高于课程标准,“从函数观点看一元二次方程”的权重低
于课程标准,苏教版教材在“不等式性质”部分的权重低于课程标准.在认知水平上,课程标准的要求在前三个水平较为均匀,未对“探究水平”作要求.而两版教材在认知水平上的侧重均是:理解>运用>识记>探究.其中,人教版“运用水平”的权重低于课程标准,两版教材“识记水平”的权重皆低于课程标准,但“理解水平”的权重皆高于课程标准,“探究水平”权重皆超出课程标准.
4 补充分析
SEC一致性分析方法在整体判断上具有很大优势,原有框架主要针对考查题目的认知水平,其他层面是否与课标相合,有待考查.另外,缺乏针对性的微观分析也是SEC一致性模式的固有瑕疵[6].下面笔者就题目的作答类型、情境类型,以及正文的引入展开作进一步探讨.
筆者对作答类型进行统计,通过对例题习题的作答类型进行卡方检验,两版教材不存在显著性差异,说明作答类型结构相近.在新课标理念下、新高考导向下,开放性、探究性题目愈来愈成为命题趋势,也将成为评价学生数学素养的有力工具.人教版设置了开放题和推广题,苏教版设置了阅读题和猜想证明题,两版教材都充分考虑了不等式一章的非常规型题目的设置,但它们的占比皆较少.对情境类型进行统计,两版教材都设置了不同领域背景的题目,情境类型较为丰富,通过对例题习题的情境类型进行卡方检验,两版教材不存在显著差异,说明情境类型分布相近.通过情境化试题来评估学生的学业或素养已经成为国内外研究的共识[7],复杂情境问题解决考查运用“整合的”逻辑、联结知识点的能力,而非仅评估“量”的获得.但是两版教材中非纯数学情境的题目占比相对较少,而以计算为主的“纯数学情境”习题占据多数.
通过对两版教材正文部分的引入与展开进行梳理,发现人教版教材采用的方式更为丰富,倾向于“问题情境”“图表辅助”和“探究思考”,注重数学直观,较多的运用类比、猜想等合情推理启发学生思考知识之间的联系,注重归纳思维的培养.苏教版教材更多地采用“证明推导”,为学生展示了更多证明方法,更倾向于抽象、一般的陈述,更加注重培养演绎推理的思维品质和理性精神.根据喻平教授在《数学教学心理学》中提到的命题教学设计的三种模式[8],对于“基本不等式”一节,人教版更倾向于发生型模式,苏教版更倾向于发生型模式与问题解决模式相结合,两者都十分注重命题的产生过程.
5 研究结论与启示
5.1 研究结论
人教版和苏教版教材不等式部分的例题习题与课程标准存在显著的一致性.两版教材与课程标准的偏离在内容主题和认知水平两个维度上的分布大致相同,偏离以正偏离为主.从局部来看,两版教材不等式的例题习题与课程标准仍有一定的出入,在理解水平和探究水平的侧重高于课程标准,在识记水平和应用水平的侧重低于课程标准.
5.2 研究启示
课程标准和数学教材需要随着社会经济的发展、教育理念的进步而逐步优化.能够从整体上对教材与课程标准的一致程度进行评估便是SEC一致性分析工具的价值所在,但一致性系数的高低并不能完全代表教材例题习题的水平,需要研究者辩证地分析看待.根据研究过程和研究结果,得到如下研究启示.
5.2.1 认知水平界定与编码主观性影响研究结果
在研究过程中,需要在课程标准的结果目标认知水平和例题习题的认知水平之间找到一个界定的平衡点.但认知行为动词实质上给出的是内部心理过程的划分,难以严格判断所属认知水平.因此,一方面,编码人员需要对课程标准和教材习题有深入的认识和理解;另一方面,研究者需根据研究内容对内容主题×认知水平的框架进行一定的改编.
5.2.2 整合题目资源,充分利用习题素材
研究结果发现两版教材不等式例题习题与课程标准的一致性显著,偏离以正偏离为主,体现了“下要保底,上不封顶”的课标落实理念.因此在实际教学中,教师应当首先把握课程标准,理解课程标准所提倡的多元要求,在此基础上充分利用不同版本教材的习题素材,以最大程度地启发学生的思维.另外,教师应当适当根据学生水平对习题进行改编和变式(比如苏教版教材设置的解一元三次不等式的题目),以满足不同层次学生的学习需求.
5.2.3 重视高水平认知,合理设置习题层次性
数学学科的六大核心素养都与高水平认知息息相关,而本文研究发现解一元二次不等式题目大量重复出现.笔者猜想这可能与“不等式”部分属于“预备内容”以及“不等式”涉及数学运算的核心素养有关.但高水平认知要求的渗透是不可或缺的,数学运算包含了理解算理、运用逻辑推理、综合解决问题等数学思维成分.建议教材编写者及时更新习题配置,加大开发具有应用性、开放性和探究性题目的力度.在保证习题整体性的同时,重视习题的层次性和针对性,适当加大“运用水平”和“探究水平”题目的比重.让学生更多地体会数学丰富的应用价值,认识数学深刻的思维品质,进而提升数学核心素养.
参考文献:
[1] 李秋实,刘学智.美国“课程实施调查”项目新进展:教科书与课程标准一致性分析模式研究[J].外国教育研究,2019,46(7):1528.
[2] 刘学智,马云鹏.美国“SEC”一致性分析范式的诠释与启示——基础教育中评价与课程标准一致性的视角[J].比较教育研究,2007(5):6468.
[3] Andrew C. Porter. Measuring the Content of Instruction: Uses in Research and Practice[J]. American Educational Research Association. 2002(7): 314.
[4] Gavin W. Fulmer. Estimating Critical Values for Strength of Alignment Among Curriculum, Assessments, and Instruction[J]. Journal of Educational and Behavioral Statistics,2011,36(3): 381402.
[5] 杨玉东,刘丹.教学目标测量的依据和工具——青浦实验的新世纪行动之三[J].上海教育科研,2007(10):4346.
[6] 段戴平.国外课程一致性研究范式述评及启示[J].高等理科教育,2016(6):1419.
[7] 王俊民,卢星辰,唐颖捷.国际大规模科学学业评估的试题情境比较研究——基于情境类型学的量化分析[J].中国考试,2019(2):3240.
[8] 喻平.数学教学心理学[M].北京:北京师范大学,2010:271273.
[9] 武丽莎,朱立明,王久成.数學学科核心素养高考测评与课程标准一致性研究——以2019—2021年高考数学Ⅰ试卷为例[J].数学教育学报,2022,31(3):3944+83.
[10] 朱立明.数学学科核心素养高考测评与课程标准一致分析框架的变证研究[J].教育科学,2021,37(3):5260.
[11] 林钊,周莹,路梦绮.不同版本教师用书与课程标准一致性分析——以苏教版、北师版高中数学必修(教师用书)为例[J].教学与管理,2019,769(12):7477.
[12] 龙正武,高存明,五旭刚.高中数学教材改革的创新与实践[J].课程.教材.教法,2020,40(7):8691.
[13] 徐小琴,张静.人教A版高中数学教材若干问题的商榷[J].教学与管理,2019,782(25):3839.
——依托《课程标准》的二轮复习策略

