穿越河流管道环焊缝裂纹缺陷安全性研究*

段宇航 董绍华 魏昊天 杨娜

(1.国家管网集团工程技术创新有限公司 2.中国石油大学(北京)管道技术与安全研究中心)

0 引 言

目前，世界各国广泛采用管道输送石油天然气。2021年，我国仅天然气的表观消费量就高达3 726×109m3，同比增长12.7%，增速远超石油和煤炭[1]。为了满足市场需要，2018至2030年天然气管道建设将迎来新的大发展时期，预计此期间将新建油气管道10万km。2025年，我国油气管网总长度将达到24万km，覆盖率进一步扩大，结构优化升级，储运能力明显提升[2-3]。管道工程具有施工距离长、跨越度大和穿越地理情况复杂等特点。每年的管道施工要穿越近百条河流，管道穿越河流时，由于河床表层的土壤不均匀或河水长期冲击作用而使管线附近的泥沙冲蚀、河床凹凸不平，造成露出管道设施致使其悬空，且受力情况较为复杂。长输管道通过焊接连接，环焊缝区域作为管道的主要失效点，在建设和服役过程中难免会存在未焊透、夹渣、裂纹等焊接问题，从而造成安全隐患[4-5]。因此，穿越河流管道环焊缝处极可能发生事故，威胁管道的安全运营。

在穿越河流管道方面，由小川等[6]采用ABAQUS有限元软件，研究了地质条件发生变化时对天然气输气管线强度和刚度的影响，首次在国内利用有限元法进行应力分析，对管道的悬空跨度和埋深进行了分析计算；符炜东等[7]采用ANSYS有限元软件中的Workbench平台，对涪陵-王场输气管道某穿越河流段悬空管道进行流固耦合计算，得到悬空管段应力特征云图和管道破坏模式。在含裂纹缺陷管道环焊缝安全性方面，ExxonMobil公司采用静裂纹计算模型，分析了管道裂纹位置、深度及长度、管道壁厚、错边量等因素对管道环焊缝的影响，并利用切线法提出了极限拉伸应变计算模型；ZHAO H.S.等[8]将等效应力应变关系方法(ESSRM)和传统裂纹驱动力J积分的估计法结合，建立了塑性极限载荷计算模型；吴锴等[9-10]考虑地质灾害常引起的永久地表变形，基于参数化建模技术，研究了裂纹长度、裂纹深度和强度匹配系数对裂纹尖端张开位移演化的影响。

国内外众多学者一直致力于对穿跨越段管道或管道环焊缝事故的研究，但是很少将两者结合。为此，笔者以穿越某河流的X70管道环焊缝为主要研究对象，基于管道局部悬跨段及管土相互作用的简化力学模型，考虑裂纹尖端处应力的奇异性，建立穿越河流的含裂纹缺陷管道环焊缝ABAQUS非线性有限元分析模型，研究屈服强度、焊缝匹配系数、内压及土壤承载力参数对管道断裂韧性值J积分的影响规律，得到影响管道环焊缝裂纹起裂的关键因素。以期为穿越河流管道安全运行提供理论基础和参考。

1 某穿越河流管道实际描述

1.1 管道工况分析

对所研究的天然气长输管道定期进行外检测和三轴高清漏磁内检测。检测结果表明：穿越河流的管道采用直埋方式敷设，在水流长时间冲刷作用下，土体松软液化，导致局部完全裸露而悬空，且其悬空段存在环焊缝裂纹缺陷。考虑无损检测的精度以及焊接接头各区域几何结构特点等因素，定义临界裂纹缺陷尺寸为50.0 mm×3.0 mm，即取裂纹长度为50.0 mm，裂纹深度为3.0 mm。该穿越管道的管材为X70，设计压力为10 MPa，规格参数为ø1 016 mm×25 mm；外防腐涂层采用环氧粉末，输送介质为天然气；穿越河流河水平均密度取1 020 kg/m3，流速为0～1.5 m/s。

1.2 管道受力分析

穿越河流管道悬跨段受力情况复杂，受到的静力载荷包括：管道自重和内部介质重力以及水流冲刷管道产生的浮力，计算公式为：

(1)

(2)

式中：G为单位长度管道及内部介质重量，N/m；Ff为单位长度管道同水流产生的浮力，N/m；D为管道的外径，m；d为管道内径，m；ρo为介质的密度，kg/m3；ρp为管道材质的密度，kg/m3；g为重力加速度，m/s2；ρw为管道所处河水的密度，kg/m3。

根据Morison理论可知，管道表面流速是动态变化的[11]，故悬跨管道主要受到平行于河流方向上的拖曳力及惯性力、垂直方向上的漩涡升力作用。单位长度管道受到的水动力的计算式为：

(3)

(4)

(5)

式中：FL为作用在管道上的旋涡升力，N/m；CL为升力系数，0.31；u为河水流速，m/s；fs为涡激振荡的泄放频率，s-1，fs=Stu/D，其中St=0.2；FD为作用在管道上的拖曳力，N/m；CD为升力系数；FⅠ为作用在管道上的惯性力，N/m；CⅠ为惯性力系数。

由于河流在垂直方向上的速度、加速度近似为0，故管道垂直于河流方向上受到的惯性力及拖曳力忽略不计[12]。图1为悬跨管道几何结构及受载示意图。图2中，B为管道壁厚

图1 悬跨管道几何结构及受载剖面示意图Fig.1 Geometric structure and load section of the suspended section

1.3 管道材料性能表征

取实际载荷工况下的X70管道母材及环焊缝进行常温下的单轴拉伸试验(参照GB/T 228.1—2010)和准静态断裂韧性试验。在X70无缝钢管上截取管材，加工为标准单轴拉伸试样，试样的长度方向为管道轴向。样品母材及焊缝区各2根，共计4根，母材以B1、B2标识，焊缝区材料以W1、W2标识。经试验，得到母材区及焊缝区材料强度性能、临界断裂韧性值等，如表1所示。

表1 管道材料参数Table 1 Pipe material parameters

根据试验得到的工程应力-应变曲线，依据下式 绘出其真实应力-应变曲线，如图2和图3所示[13]。

σtrue=σnom(1+εnom)

(6)

εtrue=ln(1+εnom)

(7)

式中：σtrue为真实应力，MPa；σnom为试验得到的工程应力，MPa；εtrue为真实应变，%；εnom为试验所得的工程应变，%。

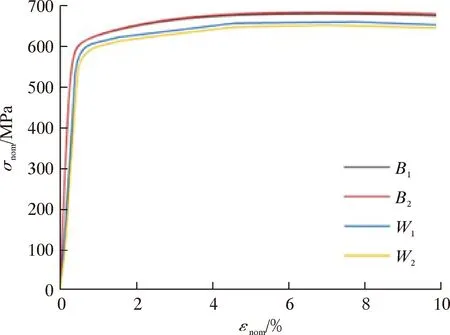
图2 试验所得管材工程应力-应变曲线Fig.2 Measured engineering stress-strain curve of pipe

图3 管材真实应力-应变曲线Fig.3 True stress-strain curve of pipe

2 含表面裂纹的管道有限元模型

本文主要根据ABAQUS软件模拟管道实际工况，对X70管材进行有限元分析。选取校正跨长为16 m的管道，其跨肩长度选取悬跨段的，即为8 m；环焊缝位于管道最中央，宽度为10 mm，两端设置土弹簧单元。考虑裂纹和管道承受载荷以及几何结构上的对称性，同时为了提高计算效率，通过非线性数值仿真软件ABAQUS建立含局部外表面裂纹管道环焊缝的对称模型。

2.1 管土相互作用模型

依据ASCE准则、DNV-RP-F114及SY/T 7056—2016等相关的准则确定土单元本构关系。通常情况下，土弹簧的模型本构关系将埋设管道的土壤视为均匀的，通过计算土壤的相对位移与极限承载力间的关系，来确定土弹簧的刚度。土弹簧模型如图4所示，KU、Kh、Kv分别表示3个方向上的土刚度系数[14]。

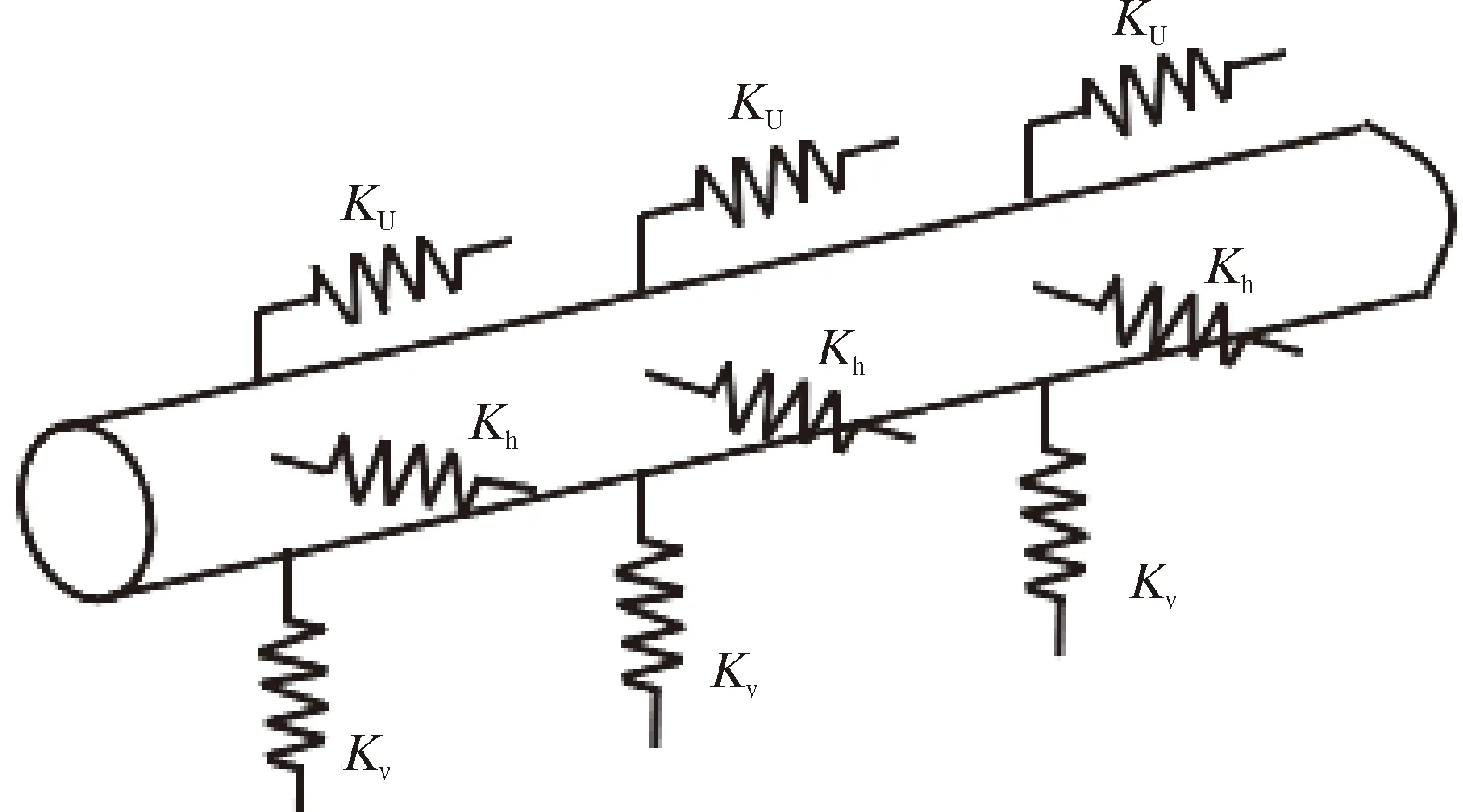
图4 土弹簧模型Fig.4 Spring model of soil

选取的土质为松黏土，土壤的抗剪强度梯度值取0.5 kPa/m，河床土壤的黏聚力取10 kPa，内摩擦角取20°，容量为21 000 N/m3。穿越河流管道悬跨段埋深1.3 m。松黏土弹簧刚度值如表2所示，管土的本构关系如图5所示。

表2 松黏土弹簧刚度计算值Table 2 Calculated spring stiffness for loose clay soils

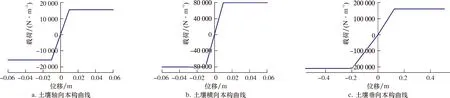
图5 土单元的本构关系Fig.5 Constitutive relation of soil elements

2.2 有限元模型

由图5可知，土体并不具有严格的线性性质。此处充分考虑土壤的非线性作用，并未使用ABAQUS自带传统线性弹簧模型，而是创新性地用连接器建立管土非线性耦合单元，如图6所示。采取实体切割划分方法在悬跨中建立管道环焊缝模型。管体网格划分采用八节点完全积分单元(C3D8)，对环焊缝附近区域网格加密，以保证缺陷处计算的准确性。基于Python参数化编程方法，采用“Canoe”型静裂纹法模拟管道环焊缝位置表面型裂纹缺陷，并可基于围线积分自动输出J积分断裂参数值。为更好地模拟裂纹在张开过程中的钝化行为，裂纹尖端采用半径为0.02 mm的楔形退化单元表征裂纹尖端应力奇异。模型采用蜘蛛网型的局部网格加密方式对裂纹面附近的网格进行细化，以消除变形过程中的应力奇异效应，改善计算收敛性，以及提高模型的计算精度。裂纹处有限元模型如图7所示。

图6 管土非线性作用模型Fig.6 Nonlinear pipe-soil interaction model

图7 管道环焊缝裂纹模型Fig.7 Pipeline girth weld crack model

模型共设置4个边界条件，并对管道模型对称面YZ面和环焊缝XY面采用对称约束，土体3个方向上的位移转角均设置为0，埋入土壤中管道最右端完全固定。设2个加载步：第一步，对管道内壁施加内压载荷；第二步，保持内压载荷不变对管道悬跨段管体施加表面应力，模拟管道受到的外力合力。

2.3 模型验证

为了验证穿越河流管道有限元数值模型的准确性及可靠性，需将施加载荷后有限元计算结果与解析法计算出的结果进行对比。在不设置管道环焊缝时，验证穿越河流管道模型的准确性，将模型计算出的管道最大变形量与基于Winkler弹性地基梁理论[15]计算结果进行比较，可知2种方法的误差为8.39%，在可接受范围内。

基于BS 7910—2019标准验证裂纹模型的准确性，将有限元计算得到的J积分通过式(8)转换为应用拉应力强度因子(KI)，将其与BS 7910标准中关于管道外表面周向裂纹的应力强度因子解析法(式(9))计算出的结果进行对比，来验证所建裂纹有限元模型的准确性[16-17]。

(8)

(9)

Yσ=Mfw{ktmMkmMmpm+ktbMkbMb×

[pb+(km-1)pm]}

(10)

式中：J为从一个裂纹面到另一个裂纹面包围裂纹前缘的线或面积分，用来表征裂纹尖端周围的局部应力-应变场，N/mm；K1为应用拉应力强度因子，N/mm；E为弹性模量，MPa；σ为应力，N/mm2；Y为应力强度修正系数，无量纲；a为原缺陷或再特种缺陷，mm；fw为有限宽度修正因子；ktm为结构不边疆性产生的对膜应力集中系数；ktb和km分别为结构不连续性及结构错位产生的应力集中系数；M为膨胀修正因子；Mkm、Mm、Mkb、Mb均为应力强度放大系数，无量纲(根据BS7910—2019规范查找使用)；pb为一次弯曲应力，MPa；pm为薄膜应力，MPa。

图8 裂纹有限元模型的验证结果Fig.8 Validation results of the crack finite element model

由于BS7910—2019规范中提供的方法适用于计算线弹性情况，所以在有限元仿真时输入纯弹性材料参数(弹性模量E为210 GPa；泊松比υ为0.3)。图8给出了ø420 mm×18 mm管道3种环向裂纹深度在不同情况下应力强度因子值的对比，图中a为裂纹深度，t为壁厚。有限元计算结果与BS 7910—2019计算所得结果较为一致，误差均未超过10%。因此，建立的管道表面裂纹有限元仿真模型较为准确。

2.4 结果分析

根据图9可视化云图，可以看出其应力在裂纹缺陷处最大，远离管道裂纹区域的数值缓慢减小，红色部分位于管道环焊缝裂纹区域。在复杂组合应力的作用下，管道环焊缝缺陷处的等效应力最大值远超过X70管线钢材料屈服强度，而其裂纹J积分值达到材料临界断裂韧性值。因此，该穿越河流管道发生裂纹扩展，最终可能发展为环焊缝处断裂失效。

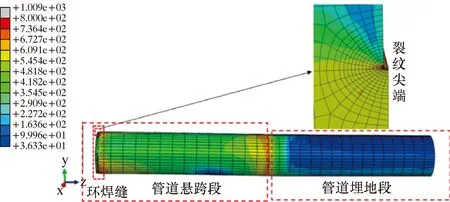
图9 穿越河流管道环焊缝等效应力云图Fig.9 Equivalent stress nephogram of girth weld of river-crossing pipeline

3 基于J 积分的敏感性分析

采用前文所述有限元模型，系统研究管道屈服强度、焊缝匹配系数、内压及土壤承载力变化，及其对穿越河流管道环焊缝裂纹处的影响规律，以识别影响管道环焊缝裂纹起裂的主要因素。

3.1 材料特性影响因素

裂纹位于环焊缝中心线位置，因此环焊接头材料主要考虑母材以及焊缝金属。基于材料应力-应变关系的本构模型，认为焊缝以及母材的应力-应变均满足幂次强化规律；在弹性阶段，其应力-应变关系满足下式：

σ=Eεσ<σy

(11)

式中：σy为材料的屈服强度，MPa；ε为材料应变，%。对于焊缝与母材弹性模量E取210 GPa。

在塑性部分，管道母材与环焊缝的应力与塑性应变关系满足下式：

(12)

式中：εp为塑性应变；εy=σy/E，为屈服应力σy对应的应变；n为材料的应变硬化系数，焊缝与母材的硬化系数相同取n=0.06[18]。

定义环焊缝的屈服强度与母材的屈服强度之比称作强度匹配系数m：

(13)

式中：σSW为环焊缝的屈服强度，MPa；σSB为母材的屈服强度，MPa。

对于母材屈服强度的影响考虑分别为600、550和500 MPa 3种情况；以及母材屈服强度σy为600 MPa时强度匹配系数为0.8、0.9、1.0和1.1的4种情况。图10分别展示了不同屈服强度母材及强度匹配系数条件下焊缝的真实应力—应变关系曲线。

基于应力的方法以力或应力作为评价和设计的参数条件，此时材料强度对结果的影响较大。横坐标河流流速是已知管道所受合力，其大小通过1.2章节中水流横向作用载荷公式(3)推算而来。图11和图12分别为不同屈服强度、不同焊缝强度匹配系数对应的J积分随河流流速变化的曲线。

图11 管道屈服强度对J积分的影响 Fig.11 Influence of pipe yield strength on J-integral

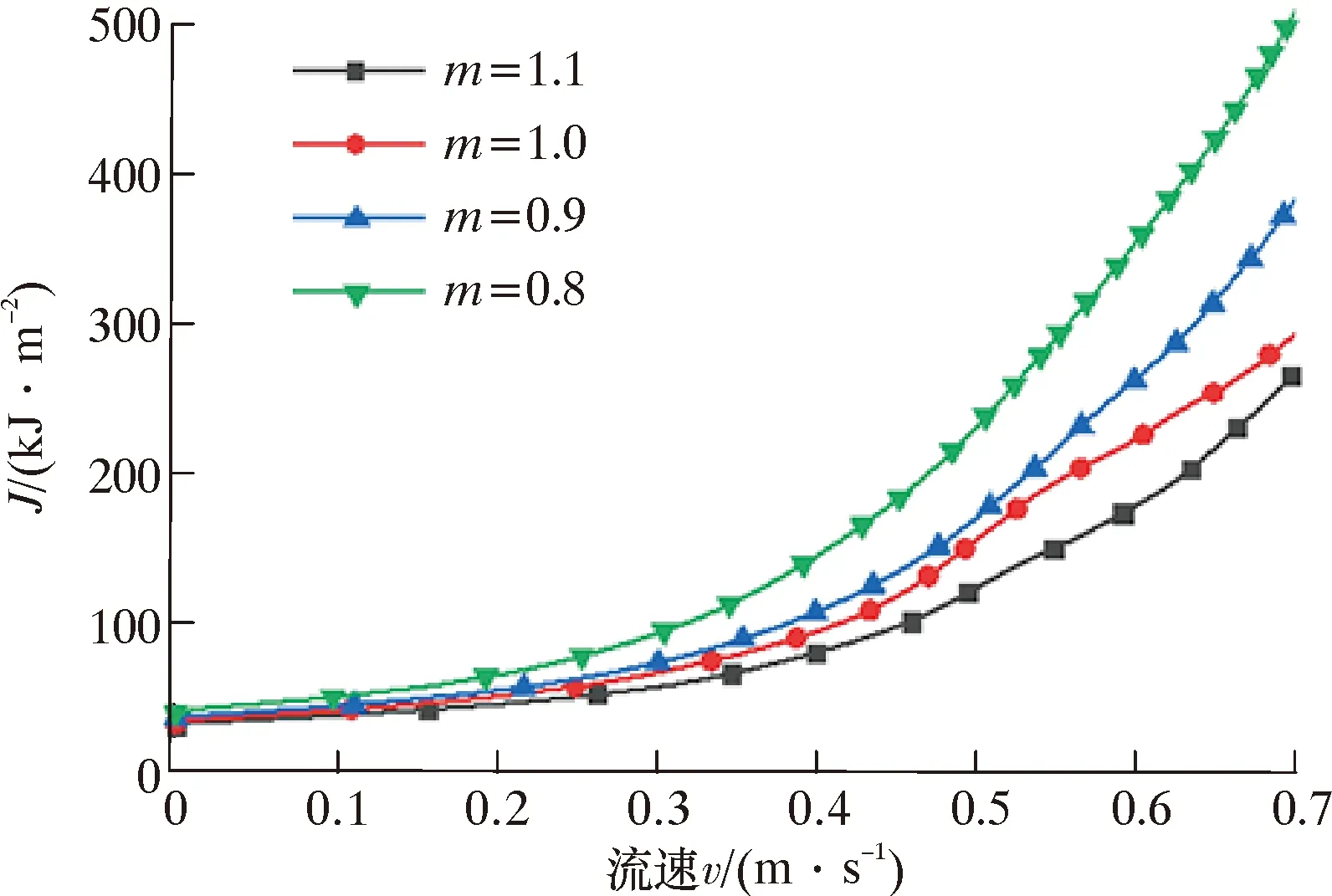
图12 焊缝强度匹配系数对J积分的影响Fig.12 Influence of weld strength matching coefficient on J-integral

从图11中可以看出，随着河流流速的逐渐增加，穿越河流管道环焊缝处J积分逐渐增大，且同一流速下，管材屈服强度越低，对应的J积分值越大。分析认为，悬跨管道所受合力为重力方向，河流流速越大，管道承受的载荷越大，J积分也随之增大；管材屈服强度高，则管道整体承载能力强，则J积分随流速增长较缓。由图12可知，焊缝强度匹配系数越高裂纹越不易进入屈服，因此相同载荷条件下强度匹配系数越高的工况，对应的J积分值就越小，且匹配系数越低，J积分与河流流速的关系曲线也更加陡峭。

3.2 内压影响

穿越河流管道受内压引起的环向应力与外界载荷作用力的共同作用而处于双轴应力状态。通常来说，在仅有内压作用的情况下，增加内压会导致J积分增加，但影响较小。仅施加内压对管道J积分结果影响如图13所示。图14为模拟实际工况下含表面初始裂纹X70管道环焊缝，在内压变化为7、8、9、10和11 MPa下对应的J积分随河流流速的变化曲线。

从图14可以看出，在内压及外界载荷共同作用下，裂纹处J积分随着河流流速的增大而增大，且低内压条件下J积分的增加幅度明显低于高内压条件下的结果。由1.3结论可知，试验所得环焊缝临界断裂韧性值JQ0.2BL为192.094 kJ/m2，该值可作为焊缝区的临界断裂韧性值JIc，可基于裂纹起裂的失效准则来确定不同内压条件下的安全河流流速，结果如图14所示。

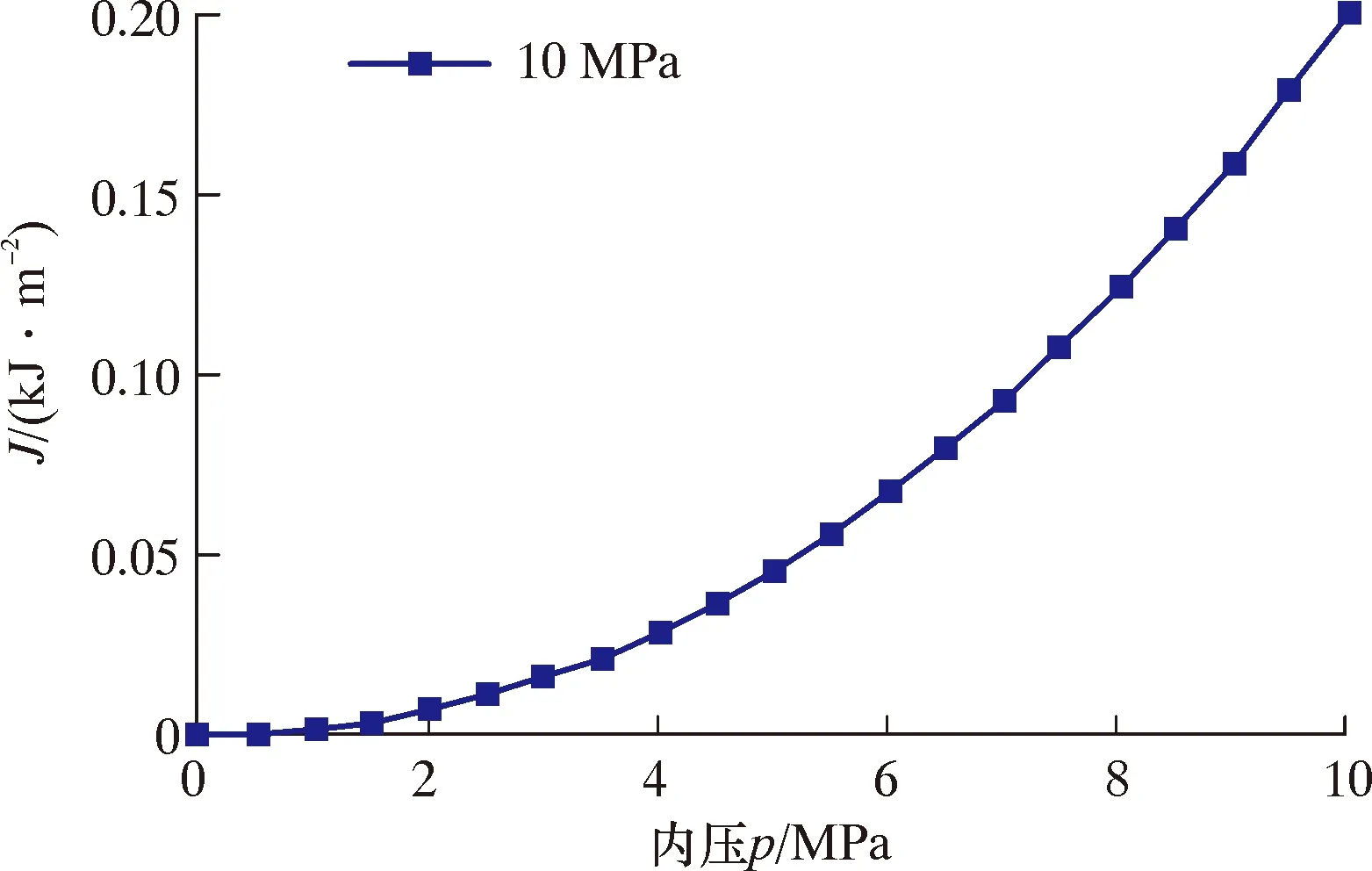
图13 仅内压作用下对J积分的影响Fig.13 Influence of pure internal pressure on J-integral

图14 双轴应力作用下内压对J积分的影响Fig.14 Influence of internal pressure on J-integral under biaxial stress

3.3 土壤承载力影响

穿越河流管道入土端土壤性质对管道的变形会产生一定程度的影响。管土间的相互作用可用土弹簧进行描述，埋深、管道类型及土壤特征均会影响土弹簧刚度取值，导致有限元计算结果的差异。如图15所示为等比例改变土壤的极限承载力，即土壤刚度(土弹簧刚度)，此条件下分析J积分随河流流速的变化规律。

图15 土壤承载力对J积分的影响Fig.15 Influence of soil bearing capacity on J-integral

从图15中可以看出，管道周围土壤承载力对环焊缝J积分有着一定的影响作用。即管道在相同载荷作用下，J积分随流速增大而逐渐增大，且在相同流速下，土弹簧刚度越小的情况对应的J积分值越大。这是由于管道周围土壤的弹性支撑作用，土弹簧刚度的增加会削弱管道整体的弯曲变形程度，减缓了复杂载荷作用下管道的变形程度。所以土弹簧刚度越大，J积分越小。

4 结 论

(1)穿越河流管道受到复杂应力的作用，运行条件恶劣。管道环焊缝处是管道薄弱环节，最易发生断裂失效，而其结构完整性是管道完整性评估的关键。以穿越某河流的X70天然气长输管道为主要研究对象进行应力分析，包括静载荷分析和由Morison理论计算的荷漩涡载荷及波浪流载。

(2)基于ABAQUS软件，建立了含裂纹穿越河流悬跨管道环焊缝非线性有限元分析模型。模型创新性地使用连接器建立管土非线性耦合单元，避免使用ABAQUS自带传统弹簧模型仅考虑土壤线性性质的弊端。基于Python参数化编程方法，建立了可导出管道裂纹驱动力的有限元模型，能够准确描述裂纹尖端钝化、起裂等断裂行为。开发了以J积分为表征的裂纹驱动力智能后处理提取方法，且经验证后发现模型输出结果准确。

(3)采用单因素敏感性分析法研究不同影响因素对J积分的影响规律。针对含相同裂纹型缺陷的管道，可以通过提高环焊缝材料屈服强度、强度匹配系数、降低管道内压来提高管道的抵抗性。由于环焊缝断裂影响参数较多，后续需进一步研究管道类型、裂纹几何尺寸等因素的影响，最终考虑各因素之间相互耦合作用下对含裂纹管道环焊缝承载能力的影响规律。