高频焊薄壁管成型仿真与分析*

蔡 绪 明

(中石化石油工程机械有限公司沙市钢管分公司)

0 引 言

由于优异的管型质量和突出的成本优势，油气管道工程用小口径薄壁钢管越来越多地选用高频焊管。但薄壁高频焊管在成型过程中钢带边缘受力和变形状态很难控制，成型工艺参数稍有偏差就可能导致钢带边缘出现波浪，影响焊接质量，甚至导致无法正常合缝和焊接。实际生产中多通过钢管试制来制定和优化生产工艺，既耽误了生产进度，又造成了材料浪费。目前有研究报道通过建模对传统的粗成型-精成型排辊成型机组的成型过程进行仿真分析来代替钢管试制[1-3]，并取得了积极进展。中石化石油机械沙市钢管分公司高频焊管机组由美国ABBEY公司引进，其先进的粗成型-TBS(过渡梁)成型-精成型工艺与通常的排辊成型技术差别较大，机架间距、数量和成型方式都不一样，文献中的仿真软件技术对该公司的借鉴意义不大。

笔者基于美国ABBEY高频焊管机组对成型过程进行建模，通过分析不同轧辊的位置变化对钢带边缘变形量的影响，计算钢带边缘变形最佳时的工艺参数用于实际钢管生产，并通过DL245M ø406.4 mm×6.0 mm高频焊管的批量生产验证，取得了较好的效果。

1 模型创建和处理

ABBEY高频焊管机组的成型一般包括粗成型、TBS成型和精成型3个阶段。钢带在每个阶段都会产生较大的塑性变形，同时与各道次的上下辊和弯边辊发生滚动摩擦接触。

1.1 几何建模

采用ANSYS 几何建模编辑工具SCDM，按照提供的二维图进行三维几何建模。本文采用ø219.1、ø406.4和ø610.0 mm共3种辊型建立高频焊管成型仿真模型，用D406.4典型辊型进行全流程仿真分析，成型辊组整体装配示意图见1。

1.2 材料选择

材料选用常用的L290钢带，规格为1 276 mm×6.0 mm(对应钢管规格为ø406.4 mm×6.0 mm)，采用柔性体进行模拟。考虑到钢带在成型压制过程中塑性变形较大，选用双线性等向强化材料模型来设置钢带的材料属性：屈服强度290 MPa，切线模量为8.60 GPa[4-5]。

图1 成型辊组整体装配示意图Fig.1 Assembly diagram of the shape-forming roller set

1.3 有限元模型创建

辊组采用高强结构钢，在分析中视为刚性体，不考虑其弹性变形，采用实体建模[6-9]；钢带为连续带状体，在成型压制过程中厚度方向的变形量远小于其他方向，故采用壳体建模[10-12]。将钢带建成一个面体，选取24 m长的钢带来模拟，让钢带穿过各成型阶段。因钢带经过各压辊的过程中呈对称性形变，分析模型选用的模型量以减少仿真分析的计算量。

1.4 接触联接定义

钢带与主动辊之间采用有摩擦接触[13]的方式创建接触对，设置相应的摩擦因数为0.2，假设动摩擦因数和静摩擦因数相等。钢带与从动辊之间采用无摩擦接触的方式创建接触对。通过预定义接触对，钢带在运行过程中与各辊组接触，接触部位取决于钢带的受力和变形状态。

2 整体分析与结论

2.1 D406.4规格薄壁管成型过程仿真

以粗成型下辊为基准进行定位，粗成型上辊位置决定辊缝大小。钢带厚6.0 mm，设定粗成型1#和2#辊组辊缝为6.2 mm，3#和4#辊组辊缝为6.4 mm。成型分析中设定钢带的前进速度为18 m/min，为了避免堆钢，驱动辊转速沿着钢带前进方向逐渐加快，其线速度如表1 所示。

表1 各驱动辊组线速度Table 1 Linear velocities of driving roller sets

图2为整个成型段的钢带等效塑性应变分布。图3为精成型段的钢带(管坯)的变形局部云图。可见最大等效塑性变形主要分布在钢带边缘，钢带从粗成型开始变形到精成型后成为管坯的过程中，钢带边缘的最大等效塑性变形值一直在升高，最大值达15.54%。在钢带端部(管坯截面)截取9个单元进行等效塑性应变和等效应力分析，如图4所示。图5和图6分别为等效塑性应变和等效应力的时间历程。由图5和图6可知，各单元的等效塑性应变在不同成型道次变化率不同，其中A(921428)单元在钢管底部，塑性应变在第一成型道次(1#辊组)等效塑性应变变化最快，后趋于稳定，对钢带边缘塑性应变影响大的是后面精成型道次。各单元的等效应力呈震荡态势，最大应力分布随着带钢和成型辊的接触而变化，部分接触部位的等效应力超过钢带屈服极限，D(864116)单元压力峰值甚至超过1 000 MPa。

图2 整段钢管等效塑性应变分布Fig.2 Effective plastic strain distribution of the whole steel pipe

图3 钢管过精成型段变形局部云图Fig.3 Local deformation nephogram of steel pipe passing the fine shape-forming stage

图4 钢带端部(管坯截面)9个单元分布图Fig.4 Distribution of 9 elements at the end of steel strip(pipe cross-section)

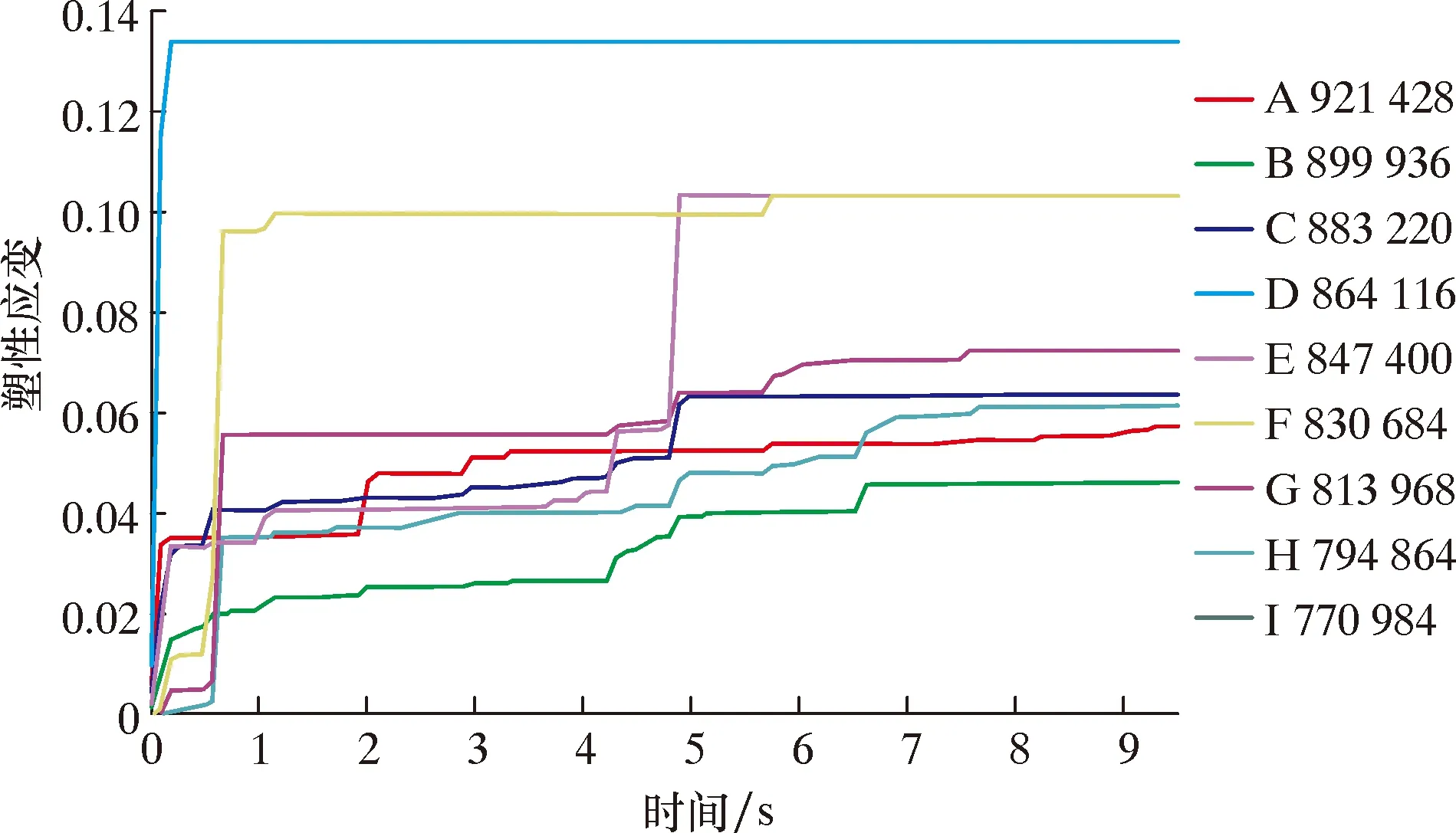
图5 钢带端部各单元在不同成型阶段的等效塑性应变时间历程Fig.5 Variation of effective plastic strain with time for elements at the end of steel strip in different shape-forming stages

图6 钢带端部各单元在不同成型阶段的等效应力时间历程Fig.6 Variation of effective stress with time for elements at the end of steel strip in different shape-forming stages

在设定件下，仿真模拟显示成型后的钢带边缘(图3管缝处)出现了周期性波浪变形，从图5的I(770984)单元曲线可以计算出钢带边缘波浪主要出现在粗成型段过弯边辊区域。经过TBS成型辊和精成型辊后，波浪虽有所减小，但仍然会影响焊接质量[14]。仿真模拟的计算结果与相同工艺条件下的实际生产出现的波浪基本一致，证明仿真分析方法可行。

2.2 不同规格管径薄壁管成型过程仿真模拟

按照2.1方法建立ø219.1和ø610.0 mm钢管的仿真模型[15-16]，进行整体模拟仿真。仿真模拟计算结果见图7和图8。由图7和图8可知，钢管成型过程均出现边缘波浪，且产生部位同样集中在粗成型过弯边辊处。

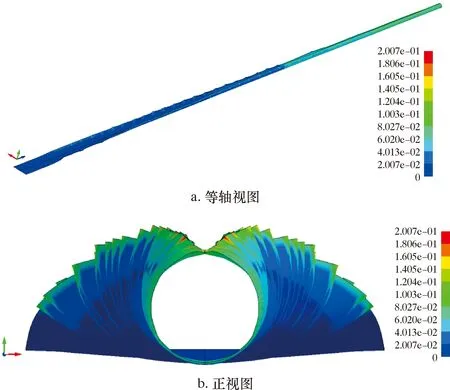
图7 管径ø219.1 mm过精成型后钢带等效塑性应变分布Fig.7 Effective plastic strain distribution of steel strip of ø219.1 mm pipe after fine shape-forming

图8 管径ø610.0 mm过精成型后钢带等效塑性应变分布Fig.8 Effective plastic strain distribution of steel strip of ø610.0 mm pipe after fine shape-forming

3 成型工艺参数影响研究

设定条件下的仿真模拟计算结果显示，钢带在粗成型过弯边辊处出现边缘波浪，将严重影响高频焊接质量。采用简化模型对直径影响边缘波浪形成的下山量和弯边高度进行仿真模拟分析，简化分析模型如图9所示，包含1#辊组、1.5#弯边辊组、2#辊组、钢带、托板、压板，钢管规格为ø219.1 mm×6.4 mm、ø406.4 mm×6.2 mm和ø610.0 mm×7.0 mm，计算采用钢带长度8 000 mm。

图9 参数研究简化分析模型Fig.9 Simplified analysis model of parameters

3.1 下山量

下山量由2#辊组底辊与1#辊组底辊的高度差来表征。除下山量外，其他工艺参数在在仿真模拟过程中保持不变，成型速度采用18 m/min。仿真模拟时将2#辊组的底辊高度相对1#辊组分别下移20、60、100、140和200 mm，进行3种规格钢管的成型仿真模拟，计算出的钢带边缘径向变形曲线如图10所示。

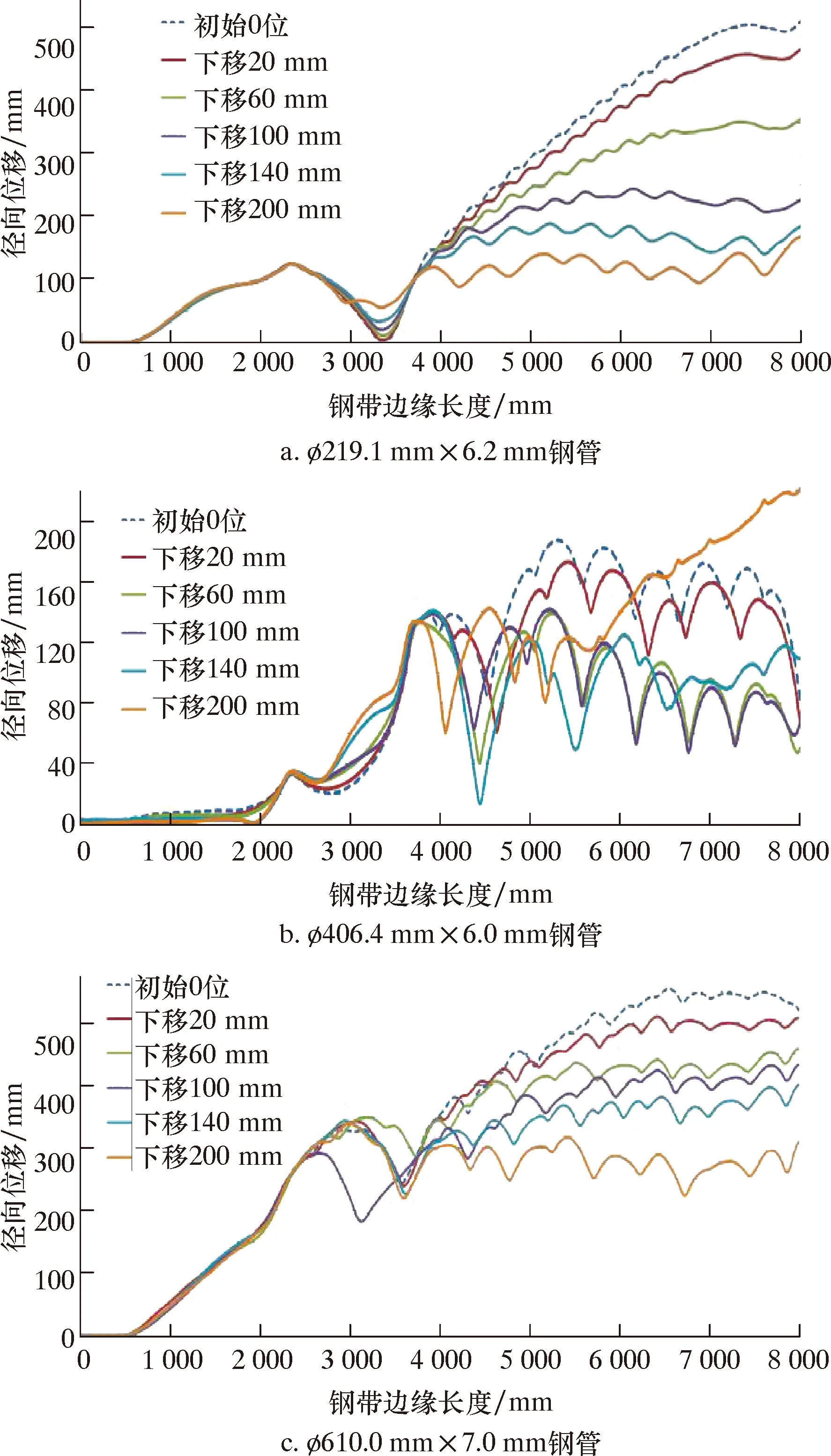
图10 不同下山量的钢带边缘径向位移曲线Fig.10 Radial displacement of steel strip edge under different downhill amounts

由图10可知，所有规格钢管的钢带边缘径向位移沿长度方向都有明显的变化，但其随下山量的变化趋势差异较大。对弯边辊(1.5#辊)至2#辊组的钢带(对应于3 800～5 500 mm)边缘的径向位移进行线性拟合，拟合曲线见图11，线性拟合度如表2所示。

表2 不同下山量钢带边缘线性拟合度Table 2 Linear fitting degree of steel strip edge under different downhill amounts

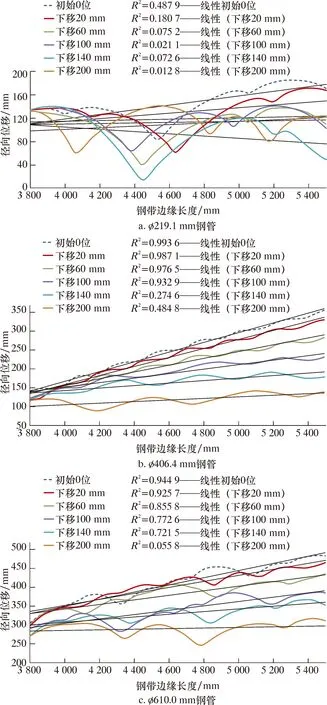
图11 不同下山量的钢带边缘径向位移线性拟合Fig.11 Linear fitting of radial displacement of steel strip edge under different downhill amounts

由表2可知，钢带边缘径向位移的线性拟合度随着下山量的增加而下降，钢带边缘波浪呈增大趋势。不同规格钢管的线性拟合度相差较大，对于ø406.4和ø610 mm钢管，可以通过降低下山量来减小钢带边缘波浪的发生趋势；但对于ø219.1 mm钢管，减小下山量对消除钢带边缘波浪的作用有限。

3.2 弯边高度对边浪影响研究

除弯边辊高度外，其他工艺参数在仿真模拟过程中保持不变，仿真模拟时将弯边辊高度相对辊花图定位的初始位置分别上移40、80、120 mm和下移40、80、120 mm，进行进行3种规格钢管的成型仿真模拟，计算出的钢带边缘径向变形曲线如图12所示。

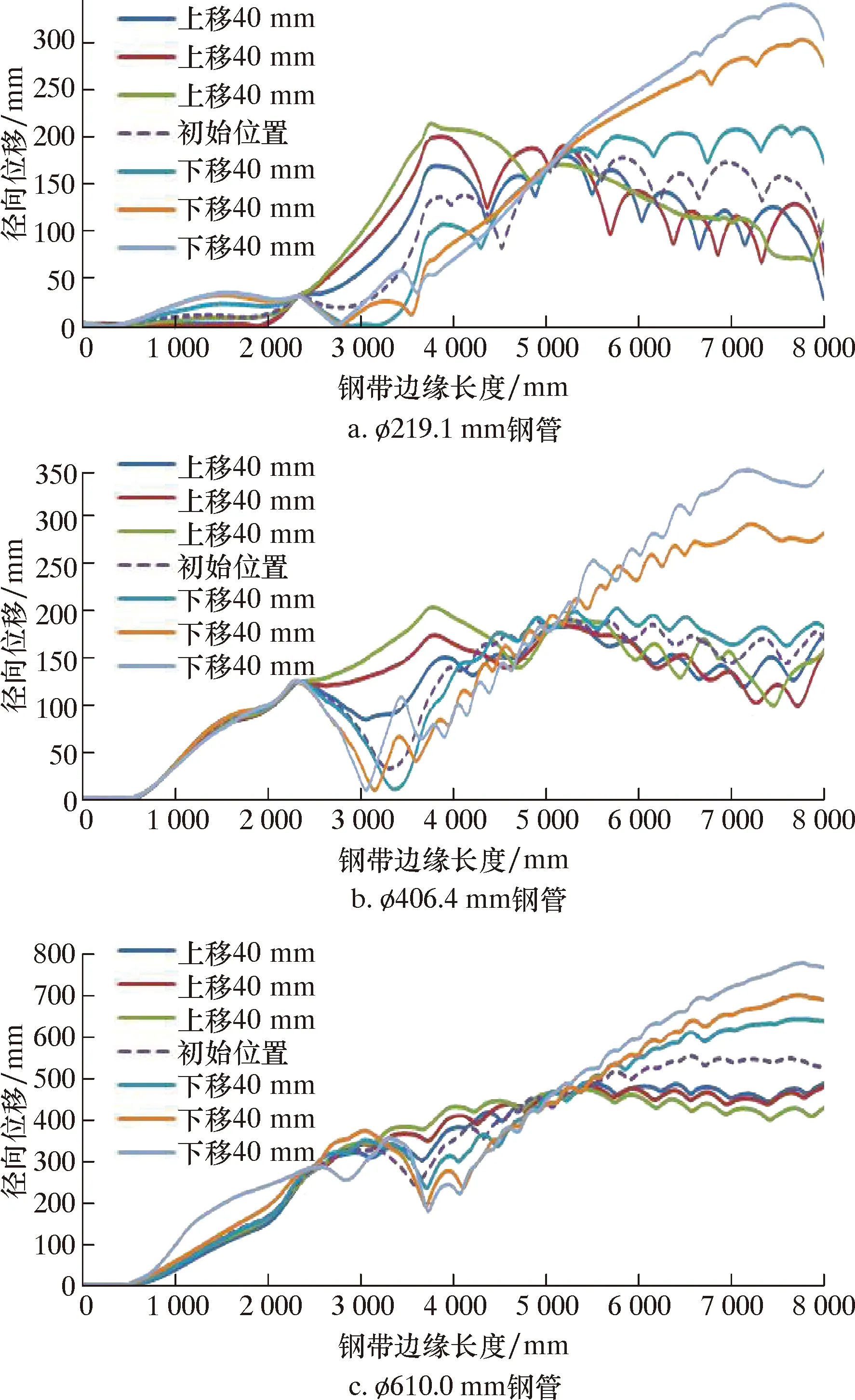
图12 不同弯边辊高度的钢带边缘径向位移曲线Fig.12 Radial displacement of steel strip edge under different edge-bending roller heights

由图12可知，所有规格钢管的钢带边缘径向位移沿长度方向都有明显的变化，但其随弯边辊高度的变化趋势差异较大。对弯边辊(1.5#辊)至2#辊组的钢带(对应于3 800～5 500 mm)边缘的径向位移进行线性拟合，拟合曲线见图13，线性拟合度如表3所示。

表3 不同弯边辊高度钢带边缘线性拟合度Table 3 Linear fitting degree of steel strip edge under different edge-bending roller heights

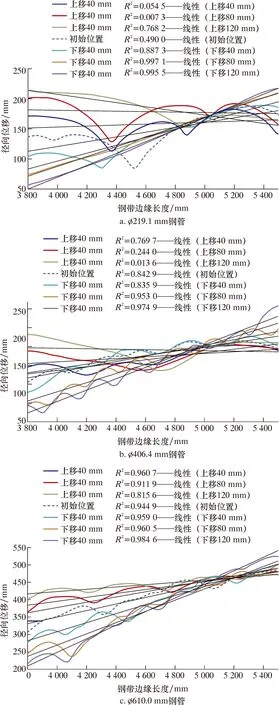
图13 不同弯边辊高度的钢带边缘径向位移线性拟合Fig.13 Linear fitting of radial displacement of steel strip edge under different edge-bending roller heights

由表3可知，钢带边缘径向位移的线性拟合度随着弯边辊下移量的增加而提高，当下移量为80～120 mm时，3种规格钢管的线性拟合度均超过0.95，钢带边缘趋近平直。但不同规格钢管的线性拟合度随弯边辊高度的变化趋势明显不同：ø610.0 mm钢管上移、下移弯边辊高度均可见证钢带边缘波浪的发生趋势，而ø406.4 mm钢管宜通过下移弯边辊高度来减小钢带边缘波浪的发生趋势；而ø219.1 mm钢管只能通过下移弯边辊高度来消除钢带边缘波浪。

考虑到弯边辊下移对降低钢带边缘波浪的积极影响，将弯边辊高度继续下移160 mm和下移200 mm，采用以上同样的模型和边界条件进行线性拟合，线性拟合度如表4所示。由表4可知，继续增大弯边辊下移量将使线性拟合度下降，不利于降低钢带边缘波浪的发生趋势。

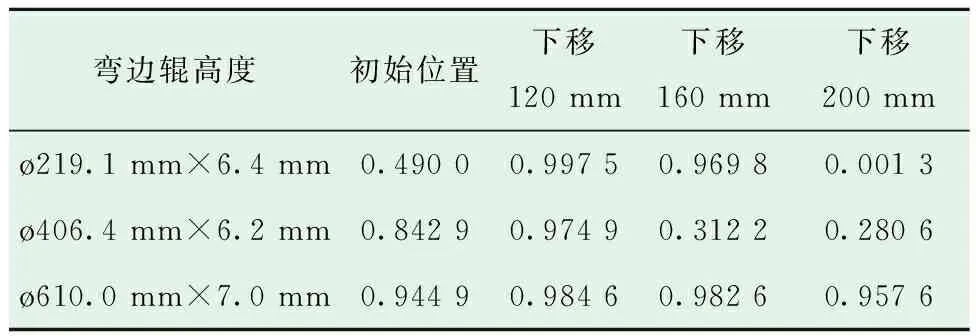
表4 不同弯边辊高度钢带边缘线性拟合度Table 4 Linear fitting degree of steel strip edge under different edge-bending roller heights

4 应用实例

4.1 技术思路

建立设备三维数字模型，形成相应模型库。根据轧制管型要求选定配套辊型，将模型进行组装。组装时按照辊花图进行初始定位，得到各辊的初始位置，包括辊的高度、角度等。然后将整体三维模型进行离散，导入LSDYNA软件中进行成型过程的仿真。计算完成查看钢管成型质量，重点关注边缘波浪的大小。通过多种成型工艺参数的匹配方案的仿真计算，确定最佳的成型工艺参数，通过批量生产进行最终验证。

4.2 实例验证

2022年5月，在L245M ø406.0 mm×6.2 mm钢管生产时，利用建模软件对确定的材料参数和成型工艺参数的匹配方案仿真计算，获得最佳的工艺参数后，在模型中确定各轧辊的空间位置。通过软件直接测量模型中各轧辊的相对距离，以粗成型1#辊组下辊为基准，后续辊组下山量如图14所示。弯边下辊空间位置数据采用类似方法测出。

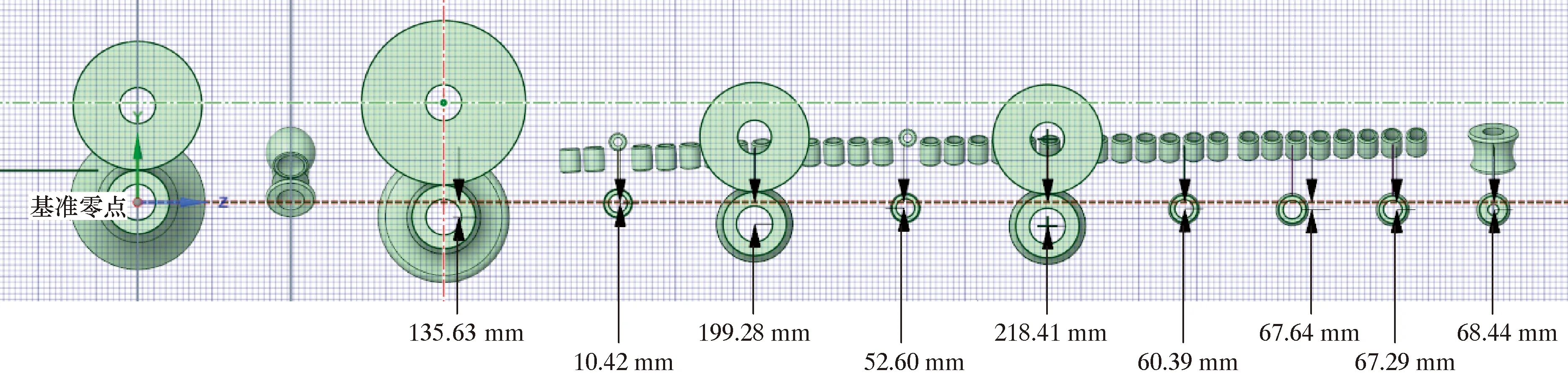
图14 成型机架辊组下山量Fig.14 Downhill amount of the roller set of the shape-forming machine

根据仿真计算出的最佳成型工艺参数进行设备调型并组织生产，共生产钢管436 t，既节省了2天的钢管试制时间，且综合材耗仅1.063，较平均材耗下降了2%，取得了良好的经济效益。

5 结 论

(1)LSDYNA软件适用于高频焊管的粗成型-TBS成型-精成型过程的仿真分析。

(2)钢带边缘波浪主要出现在高频焊管的粗成型段过弯边辊区域。

(3)钢带边缘波浪的发生趋势随着下山量的增加而升高，但对于ø219.1 mm钢管，通过减小下山量来降低钢带边缘波浪的作用有限；钢带边缘波浪的发生趋势随着弯边辊下移量的增加而减小，当下移量为80～120 mm时，钢带边缘趋近平直。