逆断层作用下碳纤维预增强管道应变响应研究*
孔天威 刘啸奔 黄微 刘城其 张东 张进 张宏
(1.中国石油大学(北京)油气管道输送安全国家工程研究中心 2.曹妃甸新天液化天然气有限公司)
0 引 言
作为油气资源重要的输送方式,管道系统被称为国家能源的“生命线”[1]。我国幅员辽阔,地形复杂,管道难以避免地会穿越地震断层。经验表明,由地震引发的断层错动带来的地面永久性变形会对管道运行安全产生巨大威胁,其中逆断层运动造成的地面位移使管道产生了较大的压缩和弯曲应变,严重时将导致管道发生屈曲失效或者破裂,由此可能引发二次灾害如燃烧爆炸等,将会给人民生命财产和自然环境带来重大损失[2]。1999年台湾集集地震和2008年汶川地震都是以逆冲为主型的地震,导致很多穿越逆断层的埋地管道发生屈曲破坏而失去服务功能[3]。
为了保证逆断层作用下埋地钢制管道的安全,国内外学者进行了大量研究,当前大多数学者采用有限元模拟的方法进行此类问题的研究。2001年,S.TAKADA等[4]将断层面附近的管段用壳单元模拟,管道远端用梁单元模拟,建立了适用于断层作用下埋地管道的梁壳耦合模型,分别研究了埋地管道在正断层和逆断层作用下的力学响应。2004年,刘爱文等[5]将远端管道看作非线性弹簧,提出了等效边界,提高了模型的计算效率。2015年,郑伟等[6]对管单元、固定边界壳单元、梁壳耦合和等效弹簧边界4种有限元模型计算得到的结果进行了对比分析,从结果差异性和计算效率两方面分别讨论了各个模型的优缺点及适用性。2016年,刘啸奔等[7]利用弯管和管单元结合的方法对逆断层作用下X80管道进行了模拟,讨论了屈曲失效行为的影响因素,并得到了管道屈曲的临界位移。2022年,赵旭等[8]用壳单元模拟管道,用实体单元模拟土壤,分析了不同逆断层错动形式对埋地钢管力学响应的影响。近年来,有学者对碳纤维复合材料(Carbon Fiber Reinforced Plastics,CFRP)修复管道问题进行了研究。2014年,O.V.TRIFONOV等[9]建立了内压和温度作用下复合材料缠绕管的应力-应变分析模型,研究了缠绕层厚度对管道应力-应变状态及承载能力的影响。2015年,M.MOKHTARI等[10]建立了走滑断层作用下碳纤维预增强埋地钢管数值仿真模型,计算了不同影响因素下管道有、无内压时发生屈曲的临界断层位移。2017年,张凯等[11]利用有限元软件对海洋立管局部CFRP建立模型并进行计算分析,通过对比裂纹尖端的应力强度因子对修复效果进行评估,得到CFRP可较好地修复含裂纹管道,恢复裂纹处承压能力的结论。
综上,目前不少学者针对逆断层作用下管道的失效机理和碳纤维复合材料对管道的保护作用进行了一定研究,但是缺乏对逆断层作用下碳纤维复合材料保护效果的定量研究,没有探明不同碳纤维复合材料参数对管道力学响应的影响。鉴于此,笔者基于三维管土耦合数值仿真模型,定量研究不同CFRP参数对管道力学响应的影响,提出穿越逆断层埋地管道的碳纤维预增强方法,以期为工程设计和现场施工提供参考。
1 碳纤维预增强埋地管道模型建立
1.1 有限元数值模型
本文基于通用非线性有限元软件ABAQUS建立三维逆断层作用下碳纤维预增强埋地管道有限元数值仿真模型。模型采用八节点六面体减缩积分实体单元(C3D8R)模拟土壤,采用四节点减缩积分壳单元(S4R)模拟管道。由于缠裹层具有类似管道的几何外形,所以采用可表征多层各向异性的连续壳单元进行模拟。管道和土壤之间切向采用罚函数进行描述,摩擦因数为0.3,法向设置为硬接触[12]。
GB/T 50470—2017《油气输送管道线路工程抗震设计规范》中规定,当采用等效边界时,应对在断层附近发生大变形、长度不小于60倍管径的管段进行有限元分析[13],LIU X.B.等[14]的研究结果也表明,断层作用下管土之间存在较大相对位移的范围在几十米以内,因此本文中管道长度设置为100 m,模拟断层的土块尺寸(长×宽×高)为100 m×10 m×5 m。土壤和管道的网格划分在靠近断层面附近进行加密处理,保证求解的精度;远离断层面的网格划分为粗网格,减少计算量。所有载荷共分3步加载:第一步,施加重力;第二步,施加管道内压;第三步,施加断层位移。模型下盘的上表面自由,底部在垂直方向上受到约束并且限制X和Z这2个方向的转动自由度,2个侧面在其法向受到约束,土壤端部固定轴向位移。上盘土壤上表面自由,其余各面在前2个加载步时均在其法向设置约束,在第三步施加统一的位移载荷来模拟断层运动。管道两端均耦合于中心参考点,并设置非线性弹簧作为边界条件,固定端非线性连接器参考点限制轴向平动位移,移动端施加与土壤相同的位移载荷。有限元模型如图1所示。
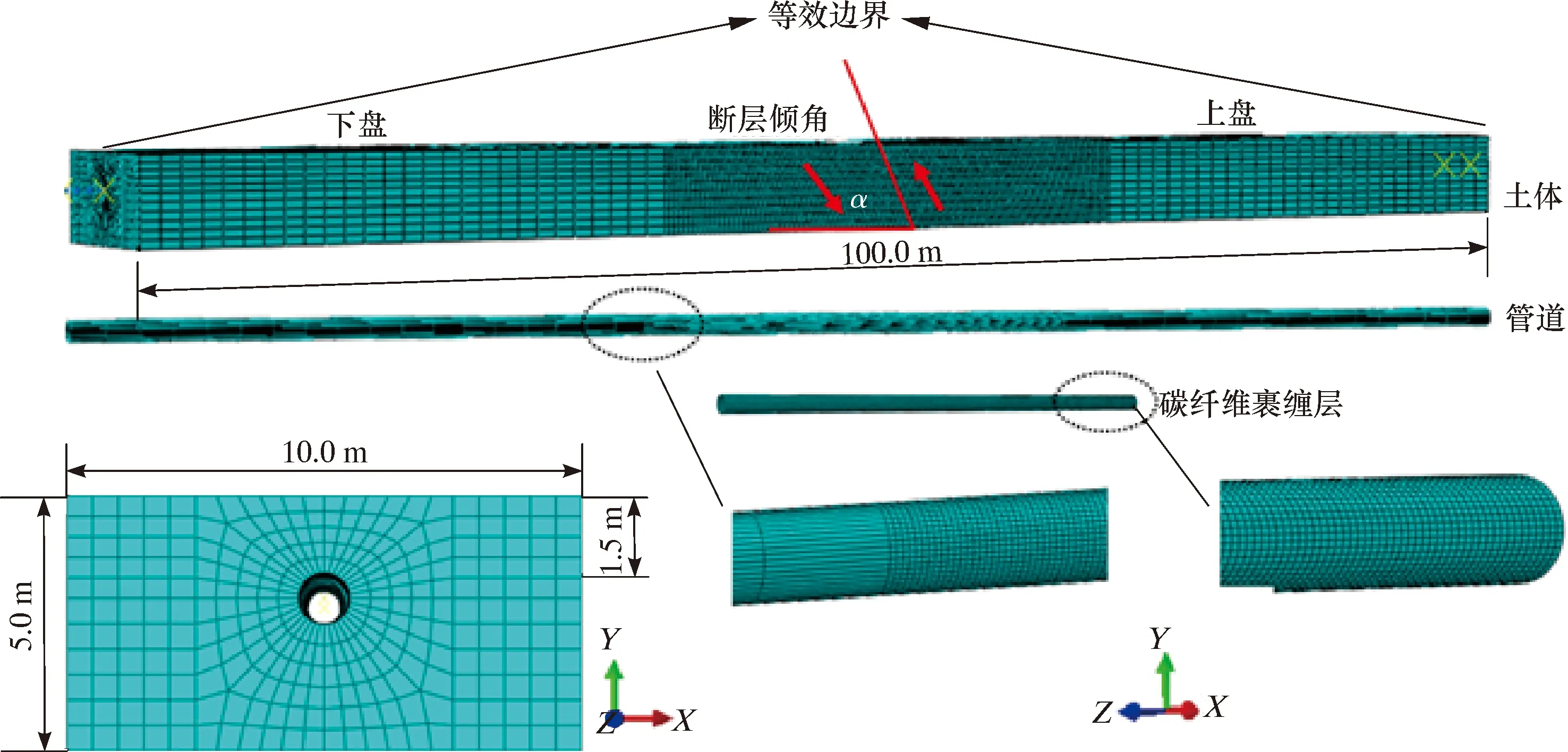
图1 有限元模型示意图Fig.1 Schematic diagram of the finite element model
1.2 模型本构与参数
管道模型参数选用X80管材,弹性模量为210 GPa,泊松比为0.3,屈服强度为555 MPa,抗拉极限为625 MPa,管外径为1 016 mm,壁厚为15.3 mm[15]。美国可靠能源系统中心在2013年研究报告中发现,对于一般的无屈服平台的管线钢,根据管材的屈服极限和抗拉极限,可以通过下式进行拟合得到完整的工程应力-应变曲线[16]:
(1)
(2)
式中:ε为工程应变;σ为工程应力,MPa;σy为屈服强度,MPa;E为弹性模量,MPa;n为应变硬化指数;Y/T为屈强比。
为满足ABAQUS软件中管材参数输入要求,将上述工程应力-应变曲线通过下式转换为真实应力-应变曲线:
εt=ln(1+ε)
(3)
σt=σ(1+ε)
(4)
式中:εt为真实应变;σt为真实应力,MPa。
通过图4和图5基本上能够明确,滚筒干燥机出口炭黑温度在前馈串级控制下,温度控制精度得到了大幅度的提升,且在联锁控制方案上也实现安全生产。
转换后的应力-应变曲线如图2所示。
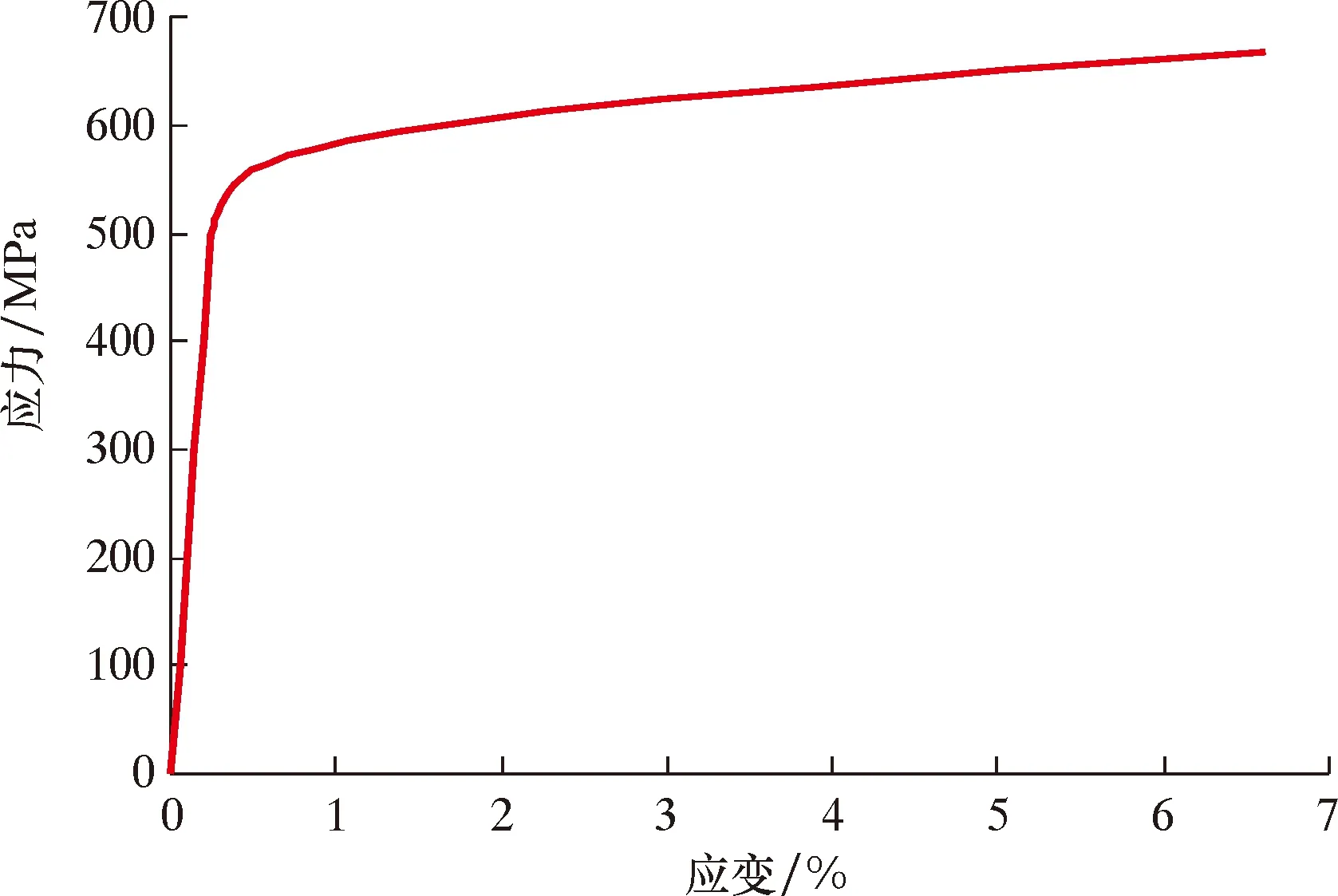
图2 X80钢材真实应力-应变曲线Fig.2 True stress-strain curve of X80 steel
采用ABAQUS中提供的Lamina本构模型描述CFRP[17],具体参数如表1所示。铺层示意图如图3所示。

表1 CFRP单层板的性能参数Table 1 Performance parameters of CFRP wrap layer
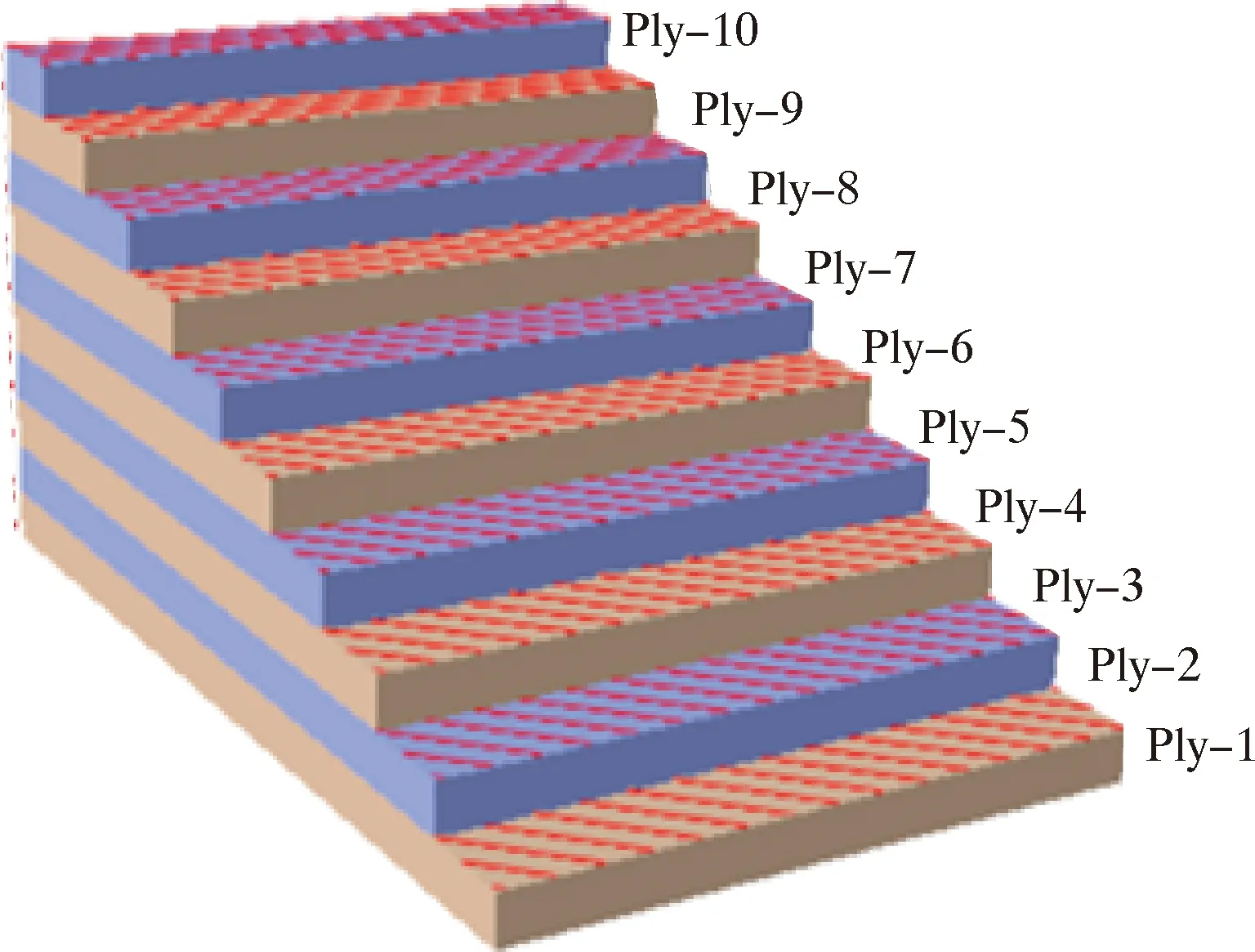
图3 碳纤维铺层结构示意图Fig.3 Schematic diagram of CFRP wrap
选取ABAQUS中Mohr-Coulomb本构模型来描述土体力学行为,该本构模型参数取值简单,同时又能够很好地描述土壤的力学行为,在岩土力学研究方面被广泛使用。该本构模型采用了下式所示的连续光滑的椭圆函数作为塑性势面[18]:
(5)
式中:ψ为剪胀角,(°);c|0为材料的初始凝聚力,Pa;e为子午面上的偏心率;q-p为应力面;Rmw控制了函数G在π平面上的形状。
土壤参数取值如表2所示。

表2 土壤参数Table 2 Soil parameters
1.3 数值模型验证
目前缺乏对逆断层作用下缠裹碳纤维埋地管道的真实试验数据,因此,根据文献[19]对逆断层作用下无内压钢制管道进行的全尺寸试验结果,验证本文无CFRP缠裹模型的准确性。试验中管道尺寸为ø114.3 mm×4.4 mm,土壤为砂土,断层位移为0.6 m。根据试验数据建立相应有限元数值仿真模型,提取断层位移为0.6 m时管顶和管底的轴向应变,并和试验结果及原文中有限元模拟结果进行对比,结果如图4所示。由图4可以看出,本文建立的有限元结果和试验结果接近程度较高,最大轴向应变的误差值为13%,证明所建立的模型精确度较高。
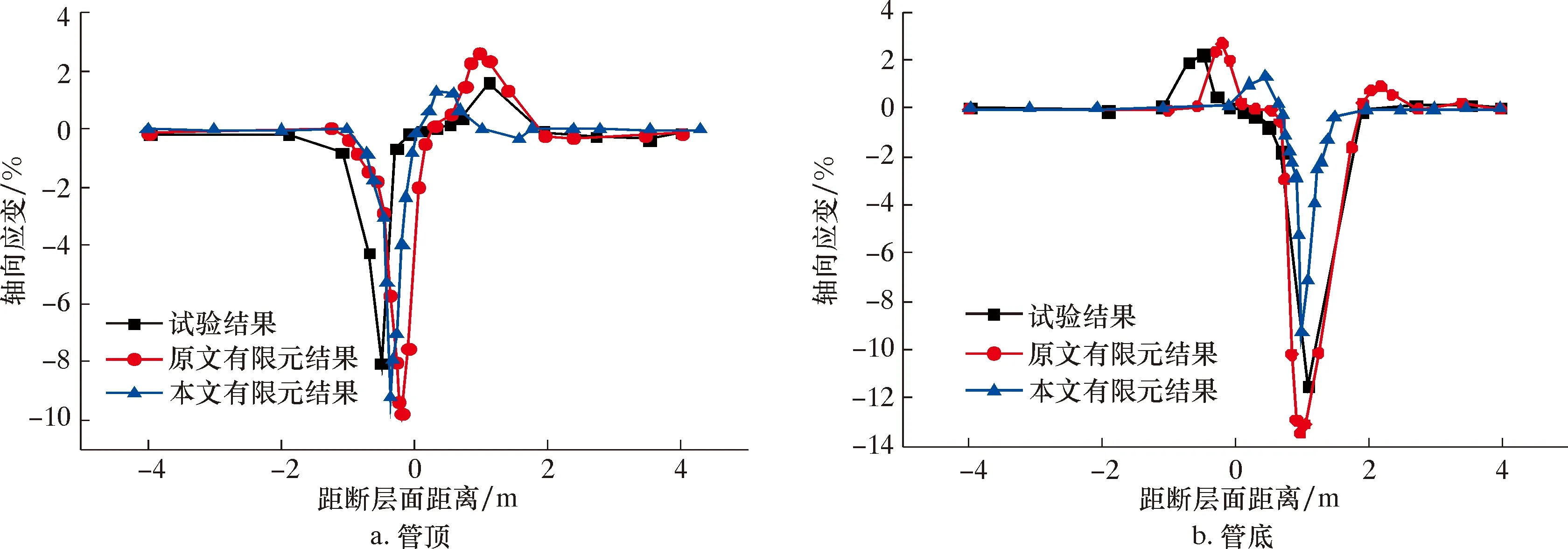
图4 有限元结果与试验结果对比图Fig.4 Finite element analysis and experimental results
1.4 等效边界模型
2 管道屈曲行为分析
逆断层作用下管道受到压弯组合作用,管道整体以受压为主。由于管道抗压性能远低于抗拉性能,所以本文选择极限压缩应变作为管道失效的判断准则。国内外对于管道局部屈曲临界应变有不同的推荐规范进行计算,应用较为广泛的有国内标准GB/T 50470—2017《输送管道线路工程抗震设计规范》与加拿大标准协会标准CSA Z662《油气管道系统》。本文采用GB/T 50470—2017中推荐的临界压缩应变公式进行计算,具体方法如下:
(6)
(7)
εr=FDPFYTFGIFNF
(8)
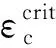
根据上式计算得到运行内压为10 MPa的情况时,管道的极限压缩应变为1.11%,当压缩应变超过该值,则认为管道发生了局部屈曲行为。
建立无CFRP缠裹、内压为10 MPa、断层倾角为60°的有限元数值计算模型。图5和图6分别为管道最大轴向压缩应变随断层位移变化曲线及应变分布图。根据图5和图6可知:在断层位移不超过1 m时,管顶和管底的最大压缩应变值差距较小;在管道发生屈曲失效的临界断层位移下,轴向压缩应变以断层面为对称面大致呈现对称分布状态,且最大压缩应变分别在断层两侧4.1 m处;随着断层位移的增加,上盘处管道管底率先发生应变突变,下盘处管道轴向应变突变相对滞后,但其应变增加速率快。图7为不同断层位移时管道的应变变化及屈曲形态图。由图7可以看出,上盘处管道率先表现出屈曲形态,下盘处管道屈曲形态出现相对滞后但变化形式更快,管道两处屈曲均为褶皱屈曲。
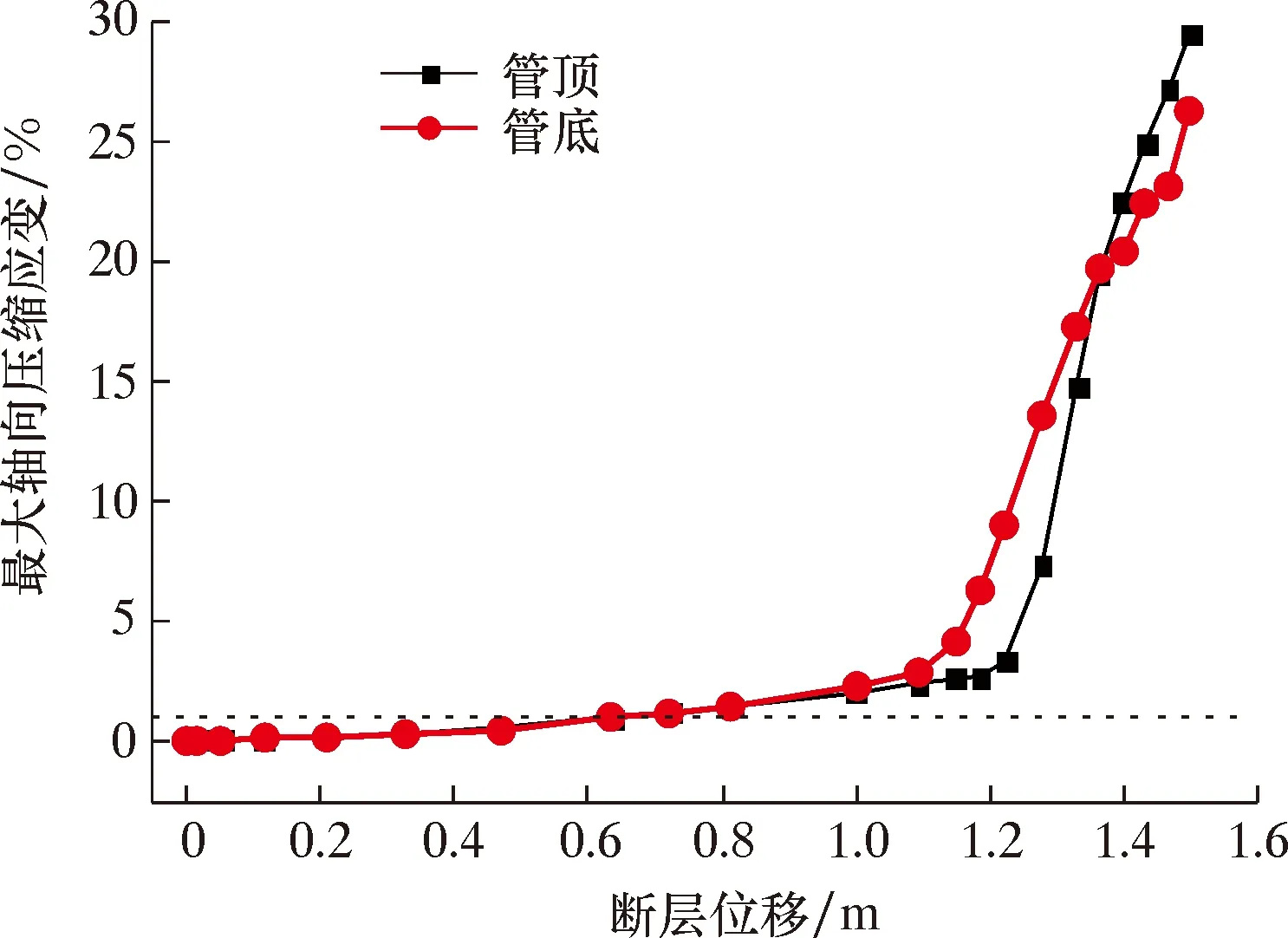
图5 管道最大轴向压缩应变随断层位移变化曲线Fig.5 Variation of maximum axial compressive strain with fault displacement
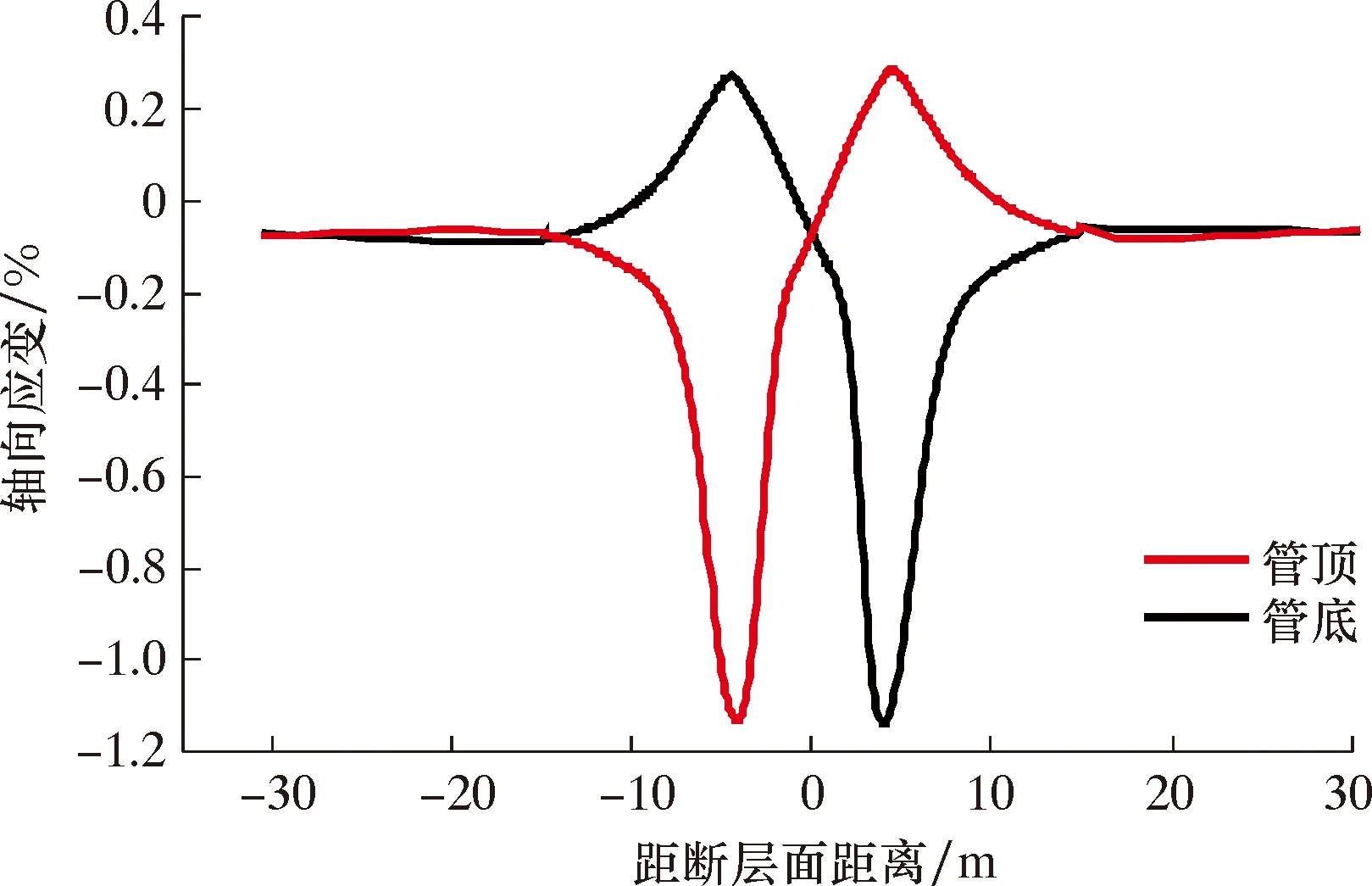
图6 管道轴向应变分布图Fig.6 Axial strain distribution of pipeline
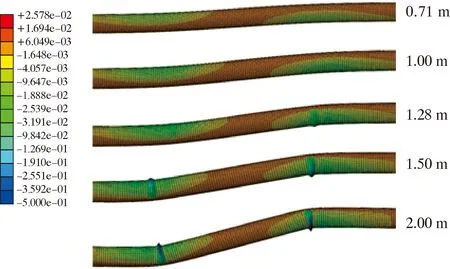
图7 不同断层位移作用下管道轴向应变分布及屈曲形态图Fig.7 Axial strain distribution and buckling pattern of pipeline under different fault displacements
3 影响因素分析
为研究逆断层作用下CFRP对埋地管道力学响应的影响,将碳纤维的缠裹厚度a、缠裹长度L和缠裹角度β作为影响因素。选取碳纤维缠裹厚度20 mm,碳纤维缠裹长度30 m,碳纤维缠裹角度15°,内压10 MPa,断层位移2 m,断层倾角60°作为基准工况。在研究某单一影响因素时,其他影响因素选取基准工况值。
3.1 不同碳纤维缠裹厚度管道响应行为
本节考虑了4种CFRP缠裹厚度(0、10、20和30 mm)。根据不同缠裹厚度时管道发生屈曲的临界断层位移和管道最大轴向压缩应变值(见表3和图8)可知,缠裹厚度为10、20和30 mm的管道最大轴向压缩应变与未缠裹CFRP时相比分别降低了41.4%、48.2%和52.4%,管道发生屈曲失效的临界断层位移分别增加了29.0%、62.0%和82.3%。计算结果表明:缠裹CFRP后,管道的轴向应变会有明显的降低,抵抗断层位移的能力有较大提升;缠裹厚度超过20 mm时,管道的应变值降低程度并不明显,抵抗断层位移的能力提升幅度也相对较小。在实际穿越断层的管道工程中,可以选择缠裹20 mm厚的CFRP对管道进行保护。

表3 不同CFRP缠裹厚度时管道屈曲的临界断层位移Table 3 Critical fault displacement for pipeline buckling under different CFRP wrapping thicknesses
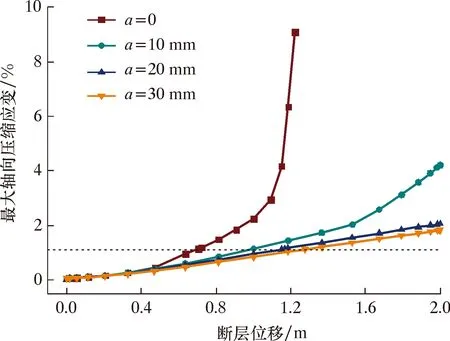
图8 不同CFRP缠裹厚度时管道最大轴向压缩应变随断层位移变化曲线Fig.8 Variation of maximum axial compressive strain of pipeline with fault displacement under different CFRP wrapping thicknesses
在上述不同工况的临界断层位移下,对比分析各工况管顶和管底的轴向应变(见图9),发现缠裹CFRP时,上盘中管道轴向压缩应变最大值均大于下盘,且管道受到的最大压缩应变均大于最大拉伸应变。图9中虚线为碳纤维缠裹层边界位置。表4为不同CFRP缠裹厚度时管道危险点距断层面的距离。由表4可知,随着缠裹厚度的增加,上盘中管道的屈曲(危险点)位置变化程度很小,而下盘中管道危险点位置逐渐远离断层面。管道上盘与下盘危险点间的距离为管道在断层错动下的危险管段长度。缠裹厚度为10、20和30 mm的管道危险管段长度比未缠裹CFRP时分别增加了6.1%、13.2%和18.0%。
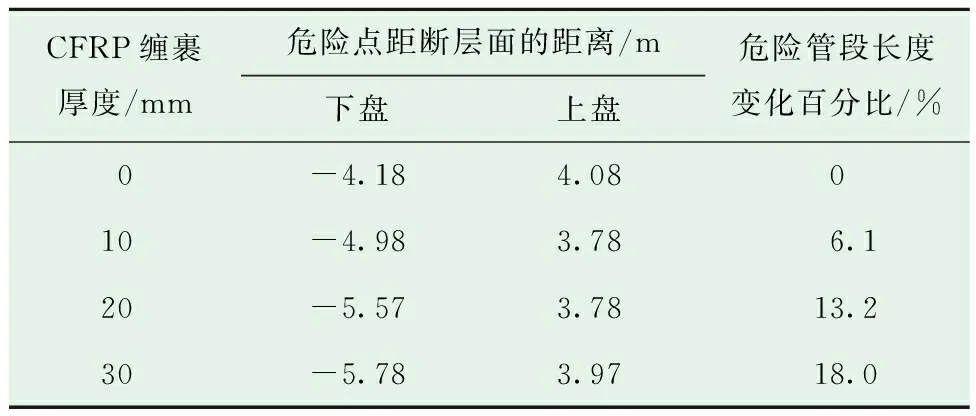
表4 不同CFRP缠裹厚度时管道危险点距断层面的距离Table 4 Distance between the pipeline dangerous point and the fault plane under different CFRP wrapping thicknesses
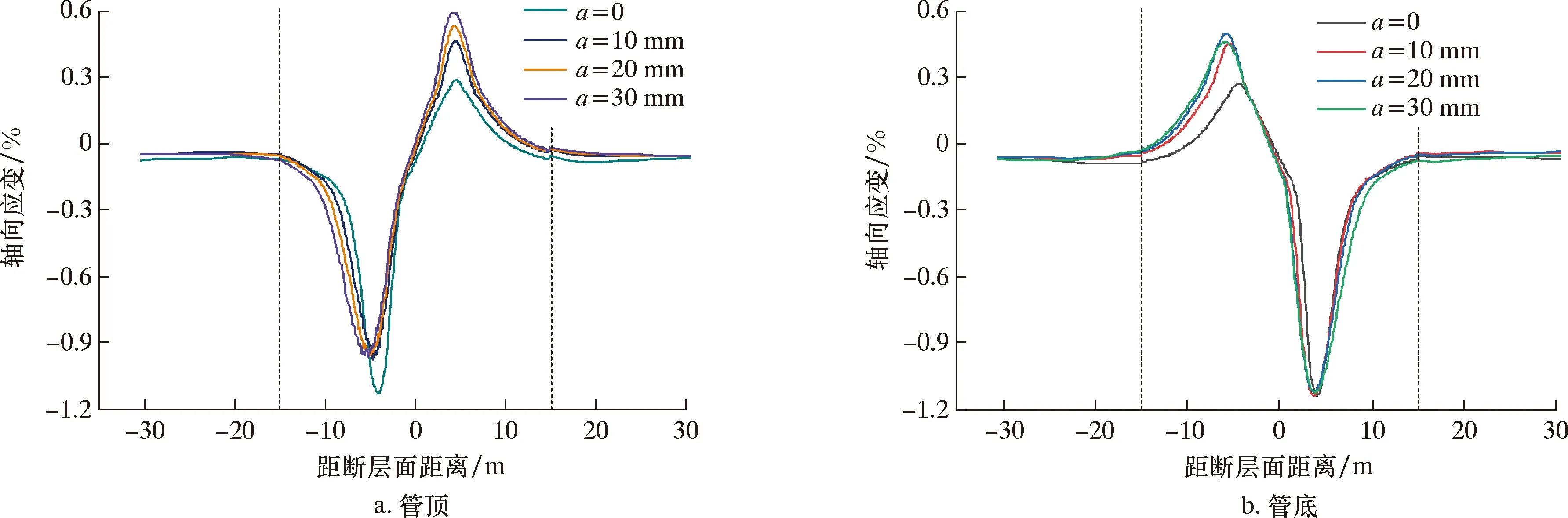
图9 不同CFRP缠裹厚度时管道轴向应变分布图Fig.9 Axial strain distribution of pipeline under different CFRP wrapping thicknesses
3.2 不同碳纤维缠裹长度管道响应行为
本节考虑了6种CFRP缠裹长度(0、10、20、30、40和50 m)。根据不同缠裹长度时管道发生屈曲的临界断层位移和管道最大轴向压缩应变值(见表5和图10)可知:缠裹长度为10、20、30、40和50 m的管道最大轴向压缩应变与未缠裹CFRP时相比分别降低了40.3%、54.9%、48.2%、43.8%和45.2%,管道发生屈曲的临界断层位移分别增加了22.5%、32.4%、62.0%、132.4%和132.4%;当断层位移小于无CFRP管道的临界断层位移时,缠裹长度对管道轴向应变的影响程度不大。但对于大位移情况,碳纤维缠裹层使得管道抵抗断层位移的能力都有了较大提升,在缠裹长度达到40 m时,这种能力提升趋于稳定。
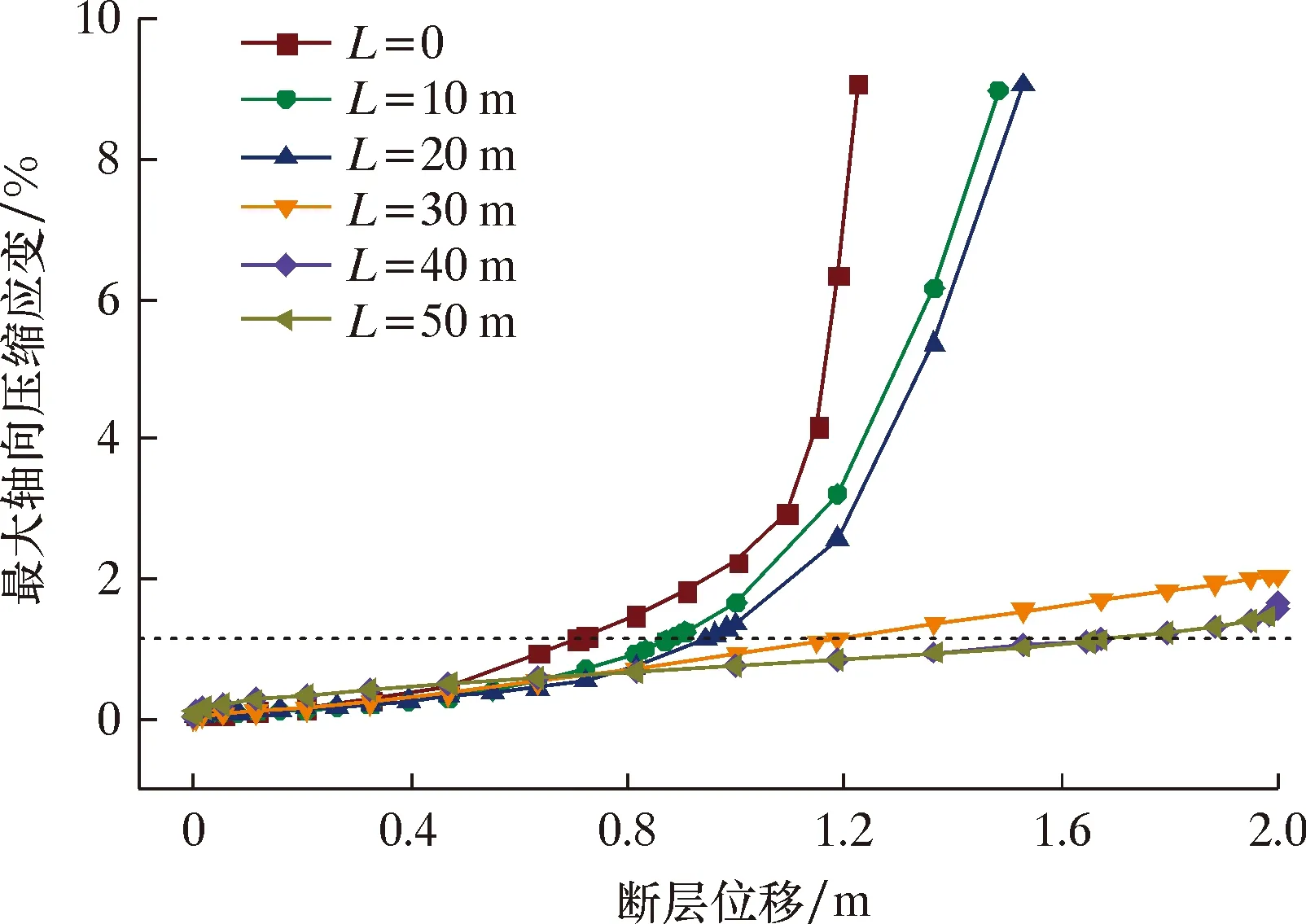
图10 不同CFRP缠裹长度时管道最大轴向压缩应变随断层位移变化曲线Fig.10 Variation of maximum axial compressive strain of pipeline with fault displacement under different CFRP wrapping lengths
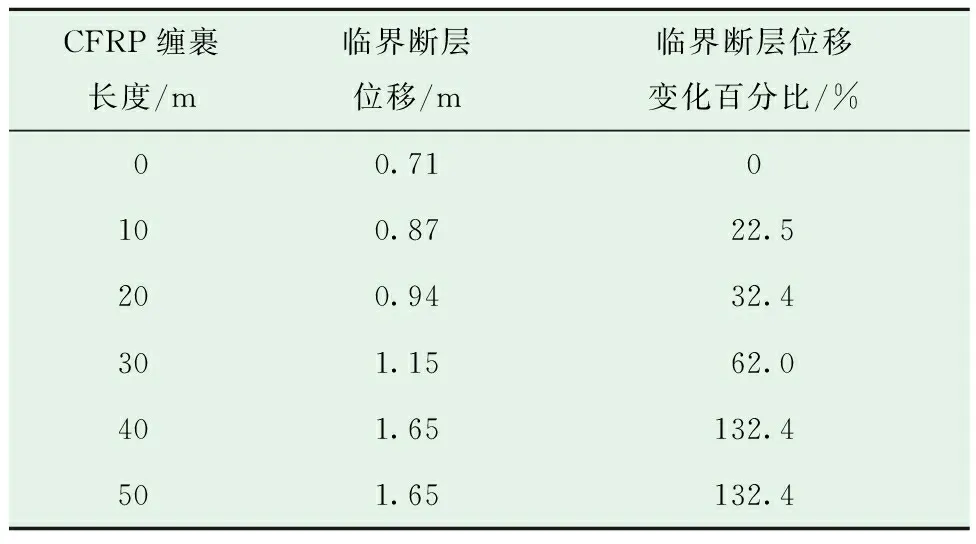
表5 不同CFRP缠裹长度时管道屈曲的临界断层位移Table 5 Critical fault displacement for pipeline buckling under different CFRP wrapping lengths
在上述不同工况的临界断层位移下,对比分析各工况管顶和管底的轴向应变(见图11),发现对于长度为10 m的情况,管道在上盘中有应变突变,屈曲位置位于上盘中缠裹层端部右侧;对于长度为20 m的情况,管道在下盘中有应变突变,屈曲失效位置位于下盘缠裹层端部左侧位置。缠裹长度为10、20、30、40和50 m的管道危险管段长度与未缠裹CFRP时相比,分别增加了70.2%、64.2%、12.3%、54.4%和54.2%,具体危险点位置见表6。由上述内容可知,裹缠层包含未缠裹CFRP管道的屈曲位置时,管道抵抗断层的能力会有较大提升,但不同缠裹长度会影响管道的屈曲位置,考虑后期修复时换管经济成本较高,而碳纤维价格相对较低,综合考虑,在实际工程中CFRP的裹缠长度在断层面各端宜大于20 m。
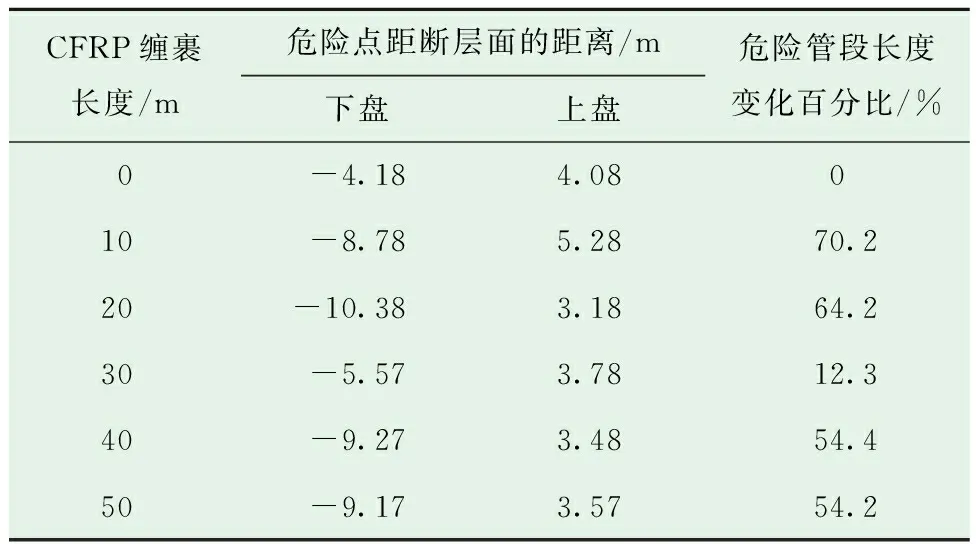
表6 不同CFRP缠裹长度时管道危险点距断层面的距离Table 6 Distance between the pipeline dangerous point and the fault plane under different CFRP wrapping lengths
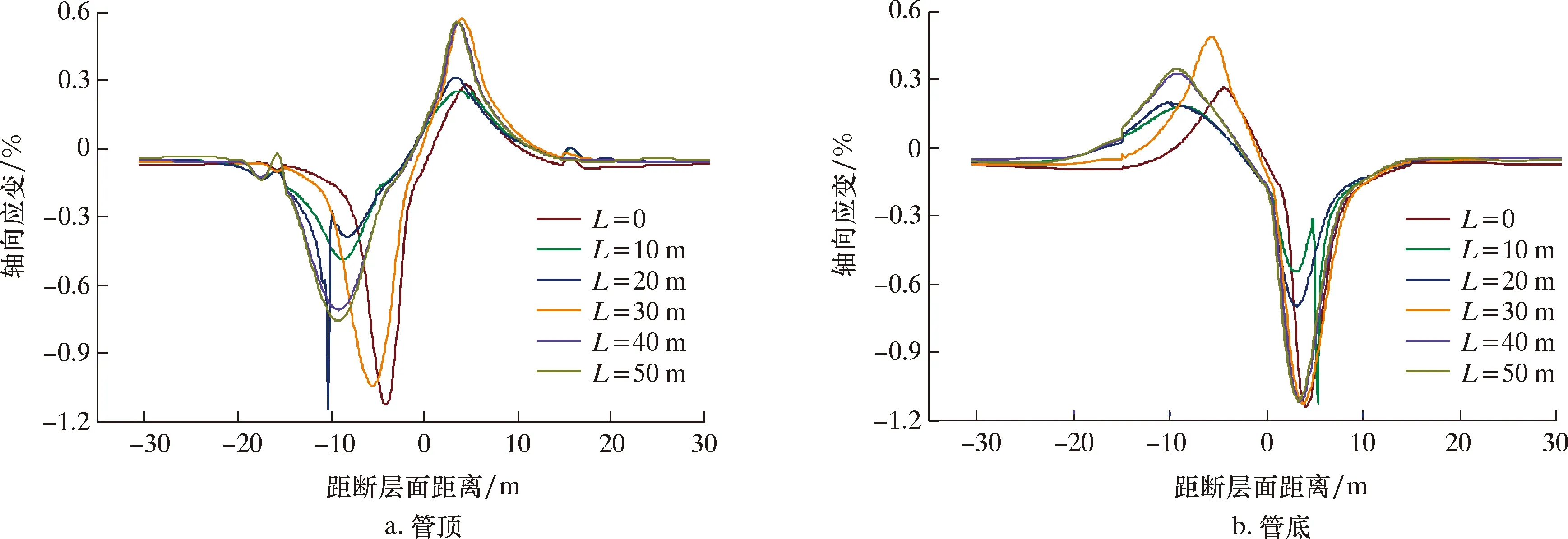
图11 不同CFRP缠裹长度时管道轴向应变分布图Fig.11 Axial strain distribution of pipeline under different CFRP wrapping lengths
3.3 不同碳纤维缠裹角度管道响应行为
本节考虑了5种CFRP缠裹角度分别为15°、30°、45°、60°和75°。
根据3.1节、表7和图12,在临界断层位移下,缠裹角度为15°、30°、45°、60°和75°的管道最大轴向压缩应变与未缠裹CFRP时相比降低了46.0%左右,管道发生屈曲的临界断层位移分别增加了62.0%、56.3%、50.7%、50.7%和43.7%。由此发现随着缠裹角度的逐渐增加,管道抵抗断层的能力会有略微降低,因为角度越小,其缠裹方向更偏向于轴向,管道的轴向应变自然也就越小,所以,在实际工程中可使CFRP缠裹角度趋向于较小值15°。

图12 不同CFRP缠裹角度时管道最大轴向压缩应变随断层位移变化曲线Fig.12 Variation of maximum axial compressive strain of pipeline with fault displacement under different CFRP wrapping angles
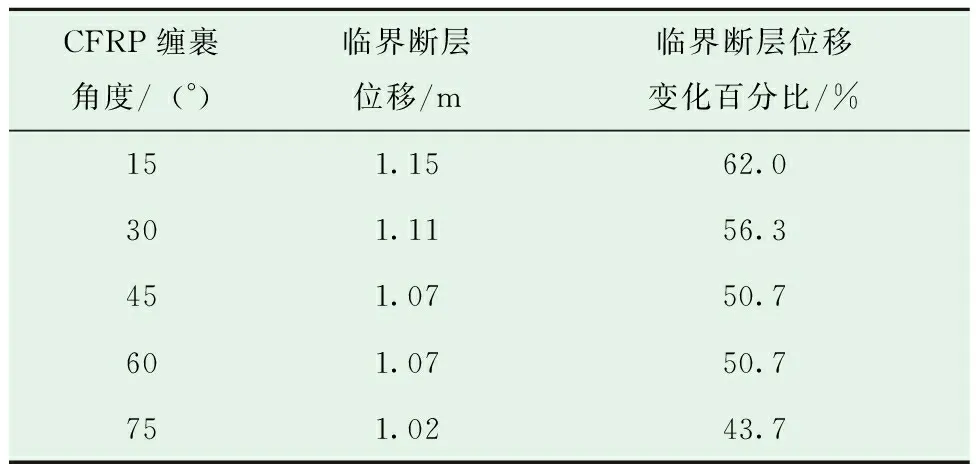
表7 不同CFRP缠裹角度时管道屈曲的临界断层位移Table 7 Critical fault displacement for pipeline buckling under different CFRP wrapping angles
在上述不同工况的临界断层位移下,对比分析各工况管顶和管底的轴向应变(见图13),发现管道仅在上盘发生屈曲失效,无论何种缠裹角度,管道屈曲(危险点)位置在上盘中距离断层面均为3.8 m左右,下盘中管道危险点均在距离断层面5.5 m左右,缠裹角度对管道危险点位置的影响十分有限。

图13 不同CFRP缠裹角度时管道轴向应变分布图Fig.13 Axial strain distribution of pipeline under different CFRP wrapping angles
4 结 论
本文通过有限元数值模拟的方法系统地研究了逆断层作用下CFRP对埋地管道力学行为的影响,探明了无CFRP缠裹与有CFRP缠裹时,不同缠裹厚度、不同缠裹长度和不同缠裹角度对逆断层作用下管道力学响应行为的影响,得到如下主要结论:
(1)对于无CFRP缠裹管道,随着断层位移增加,管道发生局部屈曲失效,下盘中管道出现明显屈曲形态滞后于上盘,但其应变变化更为迅速。
(2)缠裹CFRP后,管道屈曲及危险点位置会发生变化。缠裹层厚度越厚,管道屈曲位置离断层面越远;缠裹层较短时,屈曲位置发生在缠裹层和管道的交界处;缠裹角度不同,管道屈曲及危险点位置几乎不发生变化。
(3)相比于未缠裹CFRP的管道,在缠裹CFRP后,管道抵抗断层运动的能力有较大提升,缠裹厚度达到20 mm以上,管道应变值变化程度较小;缠裹长度达到40 m时,这种能力提升趋于稳定;不同缠裹角度对管道发生屈曲的临界断层位移影响不大,但角度较小时对保护管道更为有利。在实际工程中,针对穿越断层的油气管道,在断层面附近应当缠裹CFRP,缠裹厚度可取20 mm,缠裹长度在断层面两端宜大于20 m,缠裹角度选取较小值15°。

