水力振荡器激励力形式对减阻效率的影响分析*

石小磊 黄文君 高德利

(中国石油大学(北京)石油工程教育部重点实验室)

0 引 言

随着油气田勘探开发的不断深入，深井、超深井越来越多，井型设计逐渐由直井等单一模式向大位移井、长水平井等复杂结构模式转变。与直井相比，复杂结构井水平段增长，高摩阻扭矩、频繁托压、管柱屈曲等问题更加突出，受自身运动以及井下载荷作用，钻柱常会过早失效，严重影响钻杆的使用寿命，给钻完井作业带来极大风险和严重挑战[1]。为此，现场作业时安装水力振荡器不但能够有效减小钻柱摩擦力，增加井眼延伸距离，而且也有利于井眼轨迹控制，提高钻井效率。

国内外对水力振荡器的研究很多，主要包括工具研制和理论模型。目前，国外主要有Agitator型水力振荡器[2]和FDR型振荡器[3]，已经在多个油田应用并取得很好的效果，它可以极大地降低滑动钻进中的摩擦力和提高机械钻速，其减阻效率可达75%；国内主要有S型水力脉冲振荡工具[4]、新型涡轮水力振荡器[5-6]以及新型自激振荡器[7]等，部分工具的可靠性通过室内和现场测试。在理论方面，C.A.JOHANCSIK等[8]、H.S.HO[9]分别建立了经典的软绳模型和刚杆模型，R.POHLMAN等[10]提出了通过管柱振动降低摩阻的构想，H.D.FRIDMAN等[11]、W.LITTMANN等[12]分别建立了考虑振动器主动激励作用的管柱力学模型，并开展了试验验证。国内，李子丰等[13-16]、祝效华等[17]、王鹏等[18-19]、罗朝东等[20]、吕克华等[21]、吴志勇等[22]、ZHANG W.P.等[23]、杨龑栋等[24]、王传鸿等[25]、史怀忠等[26]、汪伟等[27]也对振动减阻问题展开了比较深入的研究，并取得了一定的研究成果。尽管一些学者从不同角度对水力振荡器的使用开展了研究，但对于水力振荡器的激励力形式，或者说地面如何调整排量控制水力振荡器的高效使用缺乏有效的理论指导，限制了水力振荡器的充分发挥。

针对该问题，笔者首先以减阻效率作为目标函数，然后考虑摩擦力的非线性建立了带水力振荡器的钻柱动力学模型，进一步引入初始条件、边界条件和连续性条件，得到了钻柱振动的有限差分方程并求解；考虑钻柱失效和水力损失等约束，对减阻因素进行参数优化。将该模型应用于实例研究，比较了不同激励力下的钻柱减阻效率，并分析了相关因素对减阻效率的影响。研究结果可为带水力振荡器钻柱的安全控制和优化设计提供一定的指导。

1 力学模型

1.1 减阻效率

无量次减阻效率是评价水力振荡器减阻效果的关键指标。本文定义了无量次减阻效率η。η表示单位时间内不带水力振荡器和带水力振荡器的钻柱之间的平均摩擦力差值与单位时间内不带水力振荡器的钻柱的平均摩擦阻力之比。其计算公式为：

(1)

式中：Fo为不带水力振荡器的钻柱单位时间振动时的平均摩擦力，N；F为带水力振荡器的钻柱单位时间内振动时的平均摩擦力，N。

1.2 振动方程

提出以下假设：

(1)钻柱是弹性杆，截面积是圆环形，井眼内壁是刚性的。

(2)钻柱与井壁均匀接触，不旋转。

(3)考虑轴向振动，忽略横向和扭转振动。

(4)采用Benson指数摩擦力模型来描述钻柱与井筒之间的摩擦力。

(5)将水力振荡器简化为具有较大刚度的弹簧。

带水力振荡器的钻柱示意图如图1所示。

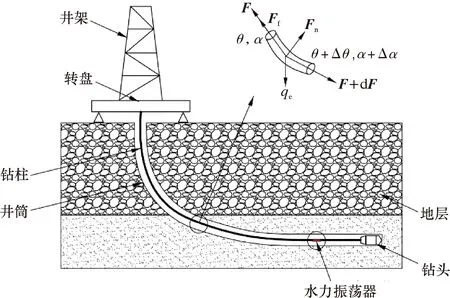
图1 带水力振荡器的钻柱示意图Fig.1 Schematic diagram of the drill string with hydraulic oscillator

钻柱由多个微元段组成，对其中一个微元进行受力分析。假设整个钻柱在初始条件下处于静态状态。因此，钻柱微分单元的平衡方程为：

F+dF+ρgAcosθds-F-μρgAsinθds=0

(2)

在振动过程中，水力振荡器可以对钻柱施加不同形式的激振力。钻柱与井壁之间的静摩擦力转化为动摩擦力。在自重、摩擦力、钻压和黏滞力的作用下，钻柱的振动方程为：

(3)

式中：U是管柱轴向位移，m；ρ是钻杆密度，kg/m3；μ是摩阻系数；g是重力加速度，m/s2；Do是钻杆外径，m；A是钻柱横截面积，m2；Ff是单位长度管柱上的摩阻，N/m；F是钻柱的轴向力，N；s是钻柱上任意一点到井口的距离，m；C是井眼内钻井液黏滞系数，N·s/m3；t是时间，s；θ是井斜角，(°)。

1.3 摩擦力模型

当速度改变时，由于强非线性特性摩擦力模拟变得很困难。本文振动模型采用Benson指数摩擦力模型[28]，如图2所示。

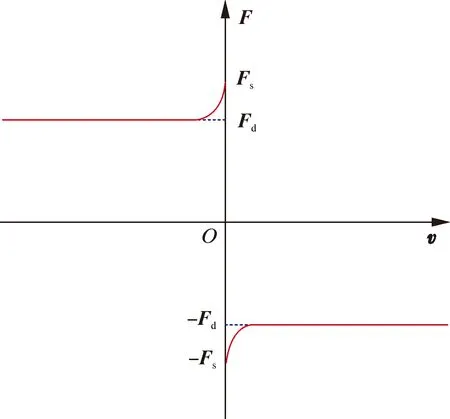
图2 摩擦力模型示意图Fig.2 Schematic diagram of the friction model

Benson摩擦力模型表示为：

Ff=Fd+(Fs-Fd)e-c|v|sgn(v)

(4)

式中：Fd是单位长度管柱的稳定滑动摩擦力，N/m；Fs是单位长度管柱的最大静摩擦力，N/m；v是管柱的轴向速度，m/s；c是指数衰减常数，s/m。

1.4 约束条件

1.4.1 钻柱疲劳失效

在深井、超深井钻进过程中，钻柱由于受到交变载荷作用引起较大的应力变化而发生失效，其中疲劳失效是最主要的失效形式。钻柱的强度校核一般基于静应力条件下进行，而实践表明，钻柱在低于屈服极限的交变应力作用下也会出现裂纹、刺穿、断裂等失效形式，因此有必要在钻柱强度校核的同时进行疲劳强度的计算。

钻柱在非对称循环应力下工作，在该状态下钻柱的疲劳强度条件为：

σmax=σm+σa≤[σr]

(5)

式中：[σr]为某一许用持久极限，MPa；σm为平均应力，MPa；σa为交变应力幅，MPa；σmax为最大交变应力，MPa。

1.4.2 水力损失

在钻井过程中，水力参数设计对井底清洗及破岩具有实际意义。不仅要计算射流的能量，还要考虑喷嘴损耗的能量。这部分能量损失可以通过循环系统压耗进行计算。钻井液循环系统总体上可分为地面管汇、钻柱内、钻头和环形空间4部分。钻井液流过这4部分时，都要消耗部分能量，使压力降低。根据流体力学中的能量方程，结合循环压耗系统的实际情况，在地面泵压受限的条件下，钻井液在循环系统中需满足的压耗约束条件为：

ΔpL=Δpb+Δpg+Δppi+Δppa+Δphyd≤ps

(6)

其中：

(7)

式中：ΔpL为循环系统总压耗，MPa；Δpb为钻头压力降，MPa；Δpg为地面管汇压耗，MPa；Δppi为钻杆内压耗，MPa；Δppa为钻杆外环空压耗，MPa；ps为钻井泵压力，MPa；FF为水力振荡器产生的激励力，kN；vh为振动器运动速度，m/s；ζ为修正系数；Q为流量，m3/s。

2 计算方法

2.1 有限差分法

为了刻画滑动摩擦力和黏滞摩擦力之间的变化，在有限差分计算过程中有必要引入很小的时间步长。通过离散化参数的定义，式(2)和式(3)用显示中心差分可以表示为：

(8)

(9)

2.2 初始条件

一般来说，有限差分方程的计算需要初始条件。换句话说，就是当式(2)右侧为0时，初始位移需要满足公式的求解。初始位移的离散化公式可以表示为：

(10)

初始速度的离散化公式可以表示为：

(11)

式中：uinitial为初始位移，m；vinitial为初始速度，m/s。

2.3 边界条件

由于钻柱顶部与大钩相连，所以钻柱顶部的轴向位移和大钩的运动位移相同。顶部边界条件可以表示为：

(12)

式中：uhook为大钩速度，m/s。

对于安装振荡器的钻柱，由于振荡器的作用，将会对钻柱施加额外的激励力，所以在振荡器上端和下端的边界条件用轴向力可以表示为：

(13)

式中：Ft为水力振荡器与钻柱连接处的轴向力，kN。

在起下钻作业中，钻头处的轴向力一般为0。但在钻进作业过程中，钻头处的轴向力与钻头和岩石接触模型有关。一般而言，钻头处轴向力的边界条件可以表示为：

(14)

式中：Wob(t)为钻压波动方程，kN。

2.4 连续性条件

当钻柱由2种或2种以上管柱组成时，钻柱的相关参数例如钻柱尺寸、重力等会因钻柱的不同而发生变化，不同的钻柱连接节点必须满足连续性条件，即相邻管段的等效轴向力在连接面上是连续的。因此可以用有限差分形式表示为：

(15)

3 激励力形式及求解步骤

3.1 激励力形式

在以往的水力振荡器研制中，没有明确各参数之间的关系。从其基本原理以及室内试验分析可以得知，当钻杆内的钻井液通过阀门时，阀门内的定阀片和动阀片相对运动，产生周期性的脉冲波作用在弹簧节上，弹簧节不断压缩其内的弹簧形成振动，从而形成周期性的压力，给予钻柱周期性的激振力[22]。这种周期性的激励力如何表达，或者说什么参数下的激励力的减阻效率最优无法得知。理论模型中，部分研究学者假设激励力为正弦函数，但不同人所取得参数不一致，不能很好地互相验证，同时不能为水力振荡器的改进提供建设性意见。

本文提出了新的激励力表达形式，主要思路是对于每一次的振动，水力振荡器所释放的能量相同，且振荡器不发生反向振动，即能量相同时，振幅和频率满足一定关系的脉冲式激励力。其表达式为：

(k=1，2，3，…，n)

(16)

式中：Fa是水力振荡器的振幅，kN；w是水力振荡器的频率，Hz；T1是工作时间，s；k是激励力的种类，无量纲。

下面给出3种激励力的曲线变化，如图3所示。

图3 水力振荡器激励力形式随时间变化关系Fig.3 Relationship between the excitation force form of the hydraulic oscillator and time

3.2 求解步骤

求解的关键思路主要分为如下几步：

(1)将减阻效率作为水力振荡器减阻效应的评价指标。

(2)在钻柱静态模型和动态模型的基础上，考虑摩擦非线性，建立带水力振荡器的钻柱力学模型；得到钻柱振动微分方程并采用有限差分法求解。

(3)考虑钻柱的疲劳失效和水力损失，对所得的关键参数进行优化。

(4)若计算结果安全满足要求，则可输出；如果计算结果不安全不满足要求，则需要调整激励力的形式。

(5)依此类推，重复过程(2)～(4)，直至输出最佳参数，筛选最合适的激励力形式。

水力振荡器轴向振动计算流程图如图4所示。

图4 水力振荡器轴向振动计算流程图Fig.4 Calculation process of axial vibration of the hydraulic oscillator

4 实例计算

基于以上模型和计算方法，研究了带水力振荡器的钻柱力学模型。JHW-X井是新疆吉木萨尔区域的一口水平井，造斜点井深为3 020 m，水平段的井斜角大约为90°，完钻井深5 520 m。JHW-X井井身结构示意图如图5所示。钻柱上部采用ø127.0 mm(5 in)钻柱，长度约为5 520 m，下部采用ø165.1 mm(6in)钻铤。转盘的平均转速为155 r/min，ROP(机械钻速)为14.25 m/h，初始钻压为50 kN。振荡器的激励载荷符合正弦分布，振幅为30 kN，频率为16 Hz。额定泵压为28 MPa。在数值模拟中，时间步长设置为4×10-4s，空间步长为3 m，计算时间为60 s。

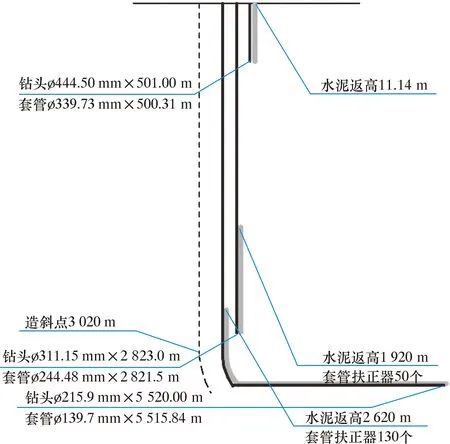
图5 JHW-X井井身结构示意图Fig.5 Casing program of Well JHW-X

4.1 振动力学分析

在进行后续的参数优化以及敏感性分析之前，首先要对比分析有水力振荡器和无水力振荡器时钻柱的力学行为，以便更好地掌握有水力振荡器的钻柱减阻规律。

有水力振荡器和无水力振荡器的钻柱轴向力和摩擦力结果随井深变化如图6和图7所示。由图6可知，有水力振荡器钻柱的轴向力几乎都位于无力振荡器的钻柱轴向力上方，且在工具的下方钻柱的轴向压力增加，从而验证了有水力振荡器的钻柱摩阻减小，大钩载荷和钻压增加，更有利于轴向力的传递。由图7可知，相对于无水力振荡器的平均摩擦力计算结果，有水力振荡器的钻柱更加有利于减阻，摩阻沿井深都有不同程度的降低，特别是在工具安放处摩擦力减小比较显著，从而说明有水力振荡器时钻柱的波动比较剧烈，更有利于钻柱的运动。

图6 轴向力随井深变化关系Fig.6 Axial force vs.well depth

图7 摩擦力随井深变化关系Fig.7 Frictional force vs.well depth

4.2 敏感性分析

在保证水力振荡器只能提供一定的能量时，如何使减阻效率最大化是现场待解决的难题。 下面分为3种情形进行分析：①频率不变，改变振幅；②振幅不变，改变频率；③振幅和频率均发生变化，也就是所说的脉冲式激励力。

(1)振幅。不同振幅下轴向力和摩擦力随井深变化如图8和图9所示。由图8可知，随着振幅的增加，大钩载荷增大，特别是在水力振荡器之上大振幅的钻柱轴向力上移，水力振荡器以下大振幅的钻柱轴向力下移，也就是说振幅增加，钻压也增大。由图9可知，振幅增加，沿井深的摩擦力均有所下降，特别是在水力振荡器附近，振幅越大，摩擦力降低的范围越大，摩擦力大幅度减小。综上所述，增大振幅可以有效降低摩擦力，提高轴向力的传递。

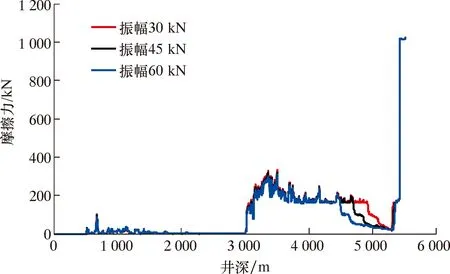
图9 不同振幅下摩擦力随井深变化关系Fig.9 Frictional force vs.well depth under different amplitudes

不同振幅下的减阻效率如图10所示。由图10可知，当振幅为30 kN时，减阻效率为9.5%；当振幅45 kN时，减阻效率为15.9%；当振幅为60 kN，减阻效率为22%。由此可见，增大振幅可以有效地提高减阻效率，且振幅是影响减阻效率的主要因素。

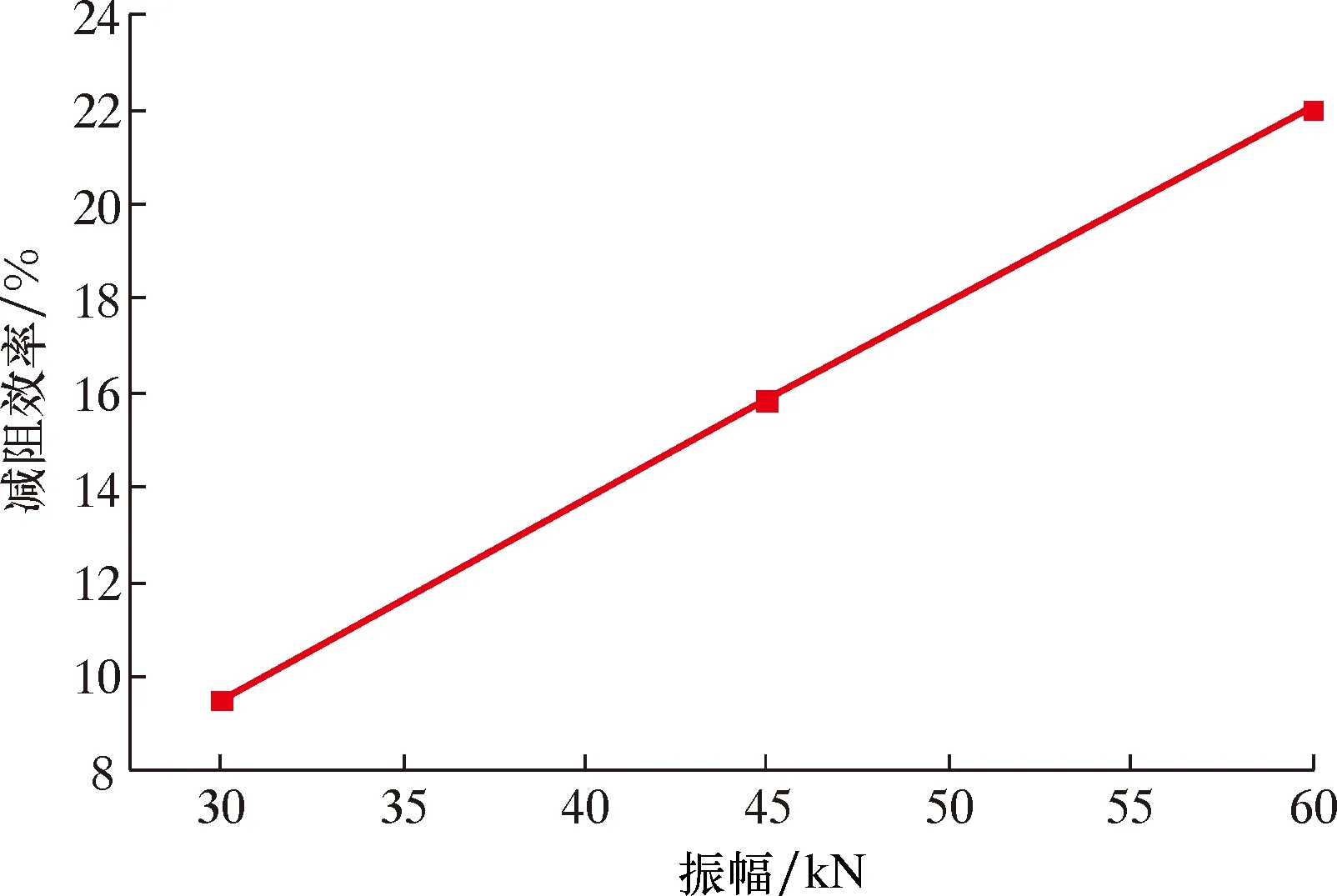
图10 不同振幅下减阻效率变化关系Fig.10 Drag reduction efficiency vs.amplitude

(2)频率。不同频率下轴向力和摩擦力随井深变化如图11和图12所示。由图11可知，频率增加，钻柱的轴向力变化不明显，意味着频率变化对轴向力的传递作用不明显。由图12可知，频率增大，除水力振荡器附近外，其余井深处的钻柱摩擦力均无明显变化，频率增加，水力振荡器处的摩擦力有很小幅度的降低。综上所述，增大频率对降低摩擦力效果不显著。

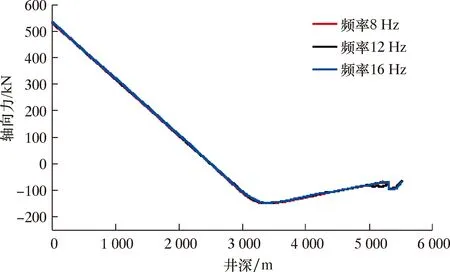
图11 不同频率下轴向力随井深变化关系Fig.11 Axial force vs.well depth under different frequencies

不同频率下的减阻效率如图13所示。当频率为8 Hz，减阻效率为7%；当频率为12 Hz，减阻效率为8.9%；当频率为16 Hz，减阻效率为9.7%。增大频率可以适当的提高减阻效率，但频率不是影响减阻效率的主要因素。

图12 不同频率下摩擦力随井深变化关系Fig.12 Frictional force vs.well depth under different frequencies

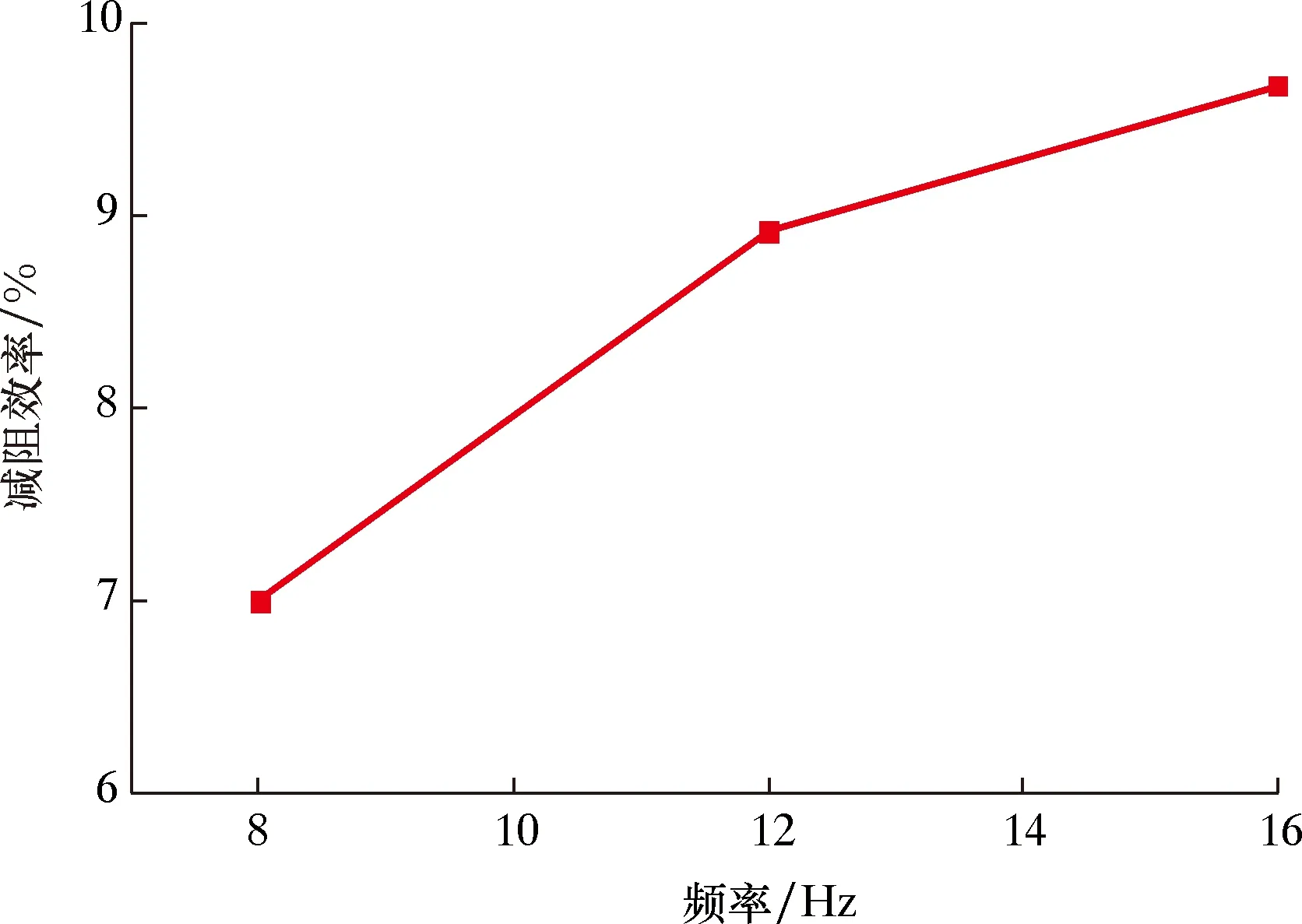
图13 不同频率下减阻效率变化关系Fig.13 Drag reduction efficiency vs.frequency

图14 不同激励力形式下轴向力随井深变化关系Fig.14 Axial force vs.well depth under different excitation force forms

(3)激励力形式。不同激励力形式下轴向力和摩擦力随井深变化如图14和图15所示。由图14可知，当水力振荡器释放的能量相同时，脉冲式激励力下的大钩载荷和钻压增加更加明显，更有利于轴向力的传递。由图15可知，脉冲式激励力下的钻柱摩擦力降低更加显著，在振幅和频率的相互配合下，结合水力振荡器的作用机理，以至于部分摩擦力的方向发生变化，大大提高了降低摩擦力的程度。综上所述，当激发的能量相同时，脉冲式激励力形式能更有效降低摩擦力，提高轴向力的传递。

图15 不同激励力形式下摩擦力随井深变化关系Fig.15 Frictional force vs.well depth under different excitation force forms

不同激励力形式下的减阻效率如图16所示。由图16可知：当选择激励力形式1时，减阻效率为6.8%；当选择激励力形式2时，减阻效率为23.8%；当选择激励力形式3时，减阻效率为38.7%。能量相同时，大振幅和大频率的激励力形式可以显著提高减阻效率。

图16 不同激励力形式下减阻效率变化关系Fig.16 Drag reduction efficiency vs.excitation force form

基于所选参数对比，影响减阻效率的主要因素和影响程度可以表示为：激励力形式>振幅>频率。

4.3 参数优化

不同激励力形式下安全系数和水力损失变化关系如图17所示。由图17可知：在能量相同时，安全系数随激励力形式1到3逐渐降低，从1.20减小为0.94。若取临界安全系数为1，则选择激励力形式2可保证钻柱的安全性。水力损失从激励力形式1到3逐渐增加，所需泵压从18 MPa到38.76 MPa，由于地面额定泵压为28 MPa。因此综合来看选择激励力形式2，即振幅45 kN和频率22.5 Hz不仅可以提高减阻效率，而且能满足钻柱安全和地面泵压的要求。

图17 不同激励力形式下安全系数和水力损失变化关系Fig.17 Safety factor and hydraulic loss vs.excitation force form

5 结 论

(1)基于非线性摩擦力模型，建立了带水力振荡器钻柱的动力学模型，以减阻效率作为目标函数，考虑钻柱失效和水力损失的约束，对激励力形式进行参数优化，为带水力振荡器钻柱的力学分析和优化设计提供了依据。

(2)增加振幅和频率均可减小摩擦力，提高减阻效率，振幅对减阻效率的影响较为显著，频率对减阻效率的影响不敏感。在激励能量相同条件下，脉冲式激励力可有效地提高减阻效率，三者的影响程度可以表示为：激励力形式>振幅>频率。

(3)振幅和频率过大的激励力形式不仅会导致钻柱疲劳失效，而且会导致过大的水力损失。因此，在地面泵压和钻柱不发生失效的前提下，为使减阻效率最大化，需要优化最佳的激励力形式，推荐最佳的激励力形式2，即振幅45 kN，频率22.5 Hz。