数据拓展和增量更新的井底压力实时预测方法*
祝兆鹏 张瑞 宋先知, 李根生, 郭勇 刘慕臣 周德涛
(1. 油气资源与探测国家重点实验室(中国石油大学(北京)) 2.中国石油大学(北京)人工智能学院 3. 中国石油新疆油田分公司工程技术研究院 )
0 引 言
井底压力是钻井方案设计和钻井参数调控中的重要参数[1]。准确计算井底压力为实现安全高效钻井提供了保障。然而,受排量、钻速、轨迹、气侵等复杂因素影响,井底压力计算是一个多参数、波动明显的复杂过程。考虑到传统经验公式误差大,数值求解方法依赖假设条件、效率低,安装随钻测压(PWD)传感器成本高、无效失真数据多等局限,难以达到现场工程应用高精度、高效率的需求,亟需提出一种新的解决方案,完善现有的井底压力预测方法。
近年来,人工智能在解决多参数、非线性的复杂工程问题方面表现出强大的优势,引领了新一代变革性钻井技术[2],实现了包括井下工况识别[3]、风险预警诊断[4-7]、机械钻速预测[8]等多方面的研究。国内外学者开始采用机器学习方法预测井底压力,在精度和效率方面得到了显著提升。D.OPOKU等[9]使用油井的生产数据(油、气、水流量和井口压力)作为输入,基于拉丁超立方抽样的算法从每个参数中随机选择样本,建立流动参数与井底压力之间的经验关系,最终选择误差最小的相关系数。多个学者[1,10-16]尝试建立不同结构的人工神经网络(ANN)以实现井底压力的精准计算。N.A.SAMI等[1]运用随机森林、K近邻、神经网络3种机器学习算法,基于地面的监测数据,实现对生产井的井底流动压力的精确预测。E.E.OKORO等[17]利用随钻测量装置收集了6口井下随钻压力数据,分别基于极端随机树和前馈神经网络算法建立了2个高精度井底压力预测模型。F.H.AL SHEHRI等[18]采用ANN、功能神经网络和长短时记忆网络(LSTM)3种模型对压裂井井底压力进行预测。为了进一步提高模型的预测精度,多个研究者开始使用混合网络模型。ZHU Z.P.等[19]建立了卷积神经网络(CNN)和LSTM的CNN-LSTM串联网络模型,证明了混合网络相比单一网络处理井底压力多元序列的优越性。Z.TARIQ等[20]基于生产井的地面数据,实现了粒子群优化算法与神经网络相结合的PSO-ANN模型,模型平均绝对百分比误差小于2.1%,优于传统的机理经验模型和ANN模型。A.M.NAIT 等[21]提出一种基于支持向量回归和萤火虫优化算法结合的预测模型,实现了多相流垂直井下的井底压力预测,结果证明了模型的高鲁棒性和准确性。LIANG H.B.等[22]通过遗传算法优化了BP神经网络的预测精度和收敛速度,为井底压力的实时预测和控制提供参考。
然而,考虑到井底压力具有较强的非线性、波动性和时序性:一方面,高温高压等复杂井段数据难以实时采集,使得数据有效信息少、分布空间受限,难以对复杂井段ECD(钻井液循环当量密度)精准计算;另一方面,由于数据驱动模型对数据的敏感特性,现有模型针对不同井段之间的迁移能力仍待提升。
因此,针对数据有效信息少、模型应用时效性差的难题,笔者提出了一种基于数据拓展和增量更新实时预测井底压力的方法。通过构建生成对抗网络(GAN)生成特定井段区间数据,增强预测模型在不同数据变化下的稳定性;利用增量数据流更新LSTM阶段预测模型,最终集成全井段预测模型;利用混合注意力机制进行井底压力智能预测模型的可解释分析等3个步骤,实现井底压力的实时精准预测。研究结果可为实现井底压力高效精准预测提供有效技术支撑,为现场工程师高效科学采取控压措施提供指导性意见。
1 智能预测方法流程
实现井底压力智能预测的整体工作流程如图1所示。工作流程包括:随钻测量数据预处理及特征工程;利用GAN网络扩充得到不同井段区间的数据集;基于现场实时采集的增量数据更新不同井段区间的预测模型;根据预测误差分配不同权重,集成全井段井底压力预测模型;通过对LSTM预测模型引入混合注意力机制,进行模型结构和预测结果的可解释性分析。

图1 井底压力智能预测方法工作流程Fig.1 Workflow of the intelligent BHP prediction method
2 数据处理
2.1 数据清洗及特征工程
本试验初始数据是新疆某口控压钻井的20万组随钻数据,其包括常规录井数据、PWD数据、钻井液数据等,涉及最大井深6 705 m,最大垂深4 942 m。
利用距离相关系数作为随钻数据相关性度量准则。系数越大,则说明2个变量之间的相关性越强。计算式为:
(1)
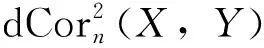
其次,考虑到钻井液性能参数对井底压力的重要影响,且避免相似度较高的多个参数同时引入扩大噪声,影响模型的稳定性,本文选择将漏斗黏度、含砂量、钻井液密度3个特征补充至原数据集。通过计算距离相关系数,最后筛选得到相关性系数大于0.5的输入特征变量共12个,分别为定点垂深、入口流量、回压泵流量、钻头深度、转速、立压、总池体积、出口流量、出口密度、钻井液密度、含砂量和漏斗黏度,随钻测压数据共8万组。
将处理完成的数据依据井深排序划分,得到60 000组浅部测压点作为训练集,20 000组深部测压点作为测试集。同时,进行数据的归一化有利于模型加快搜索寻找最优解。本研究采用max-min归一化,使特征变量映射到(0,1)之间:
(2)
式中:x表示某一特征值;xmin表示某一特征的最小值;xmax表示某一特征的最大值。
2.2 多元序列样本重构
由于钻井现场采集的随钻测压数据具有一定的时序相关性,即认为上部井底压力会对下部产生一定影响,可将井底压力的预测问题视作为多变量的序列预测问题。滑动窗口是处理序列预测问题的重要方法之一[23]。使用固定窗口长度h依次滑动长度为n的随钻数据序列,得到新的多元序列输入样本X=[xn-h,…,xt,…,x1]T和标签样本Y=[yn-h,…,yt,…,y1]T。
其中:xt=[定点垂深t-1,…,t-h,入口流量t-1,…,t-h,回压泵流量t-1,…,t-h,…,漏斗黏度t-1,…,t-h]。
3 GAN网络数据拓展
针对复杂井段有效数据少、不同井段数据波动性强的特点,本部分利用GAN网络生成不同规模的训练数据,扩充原始数据集,最后基于LSTM构建井底压力预测模型,分析不同数据规模下的试验预测结果。
3.1 GAN网络模型
GAN是一种无监督学习模型,现广泛应用于生成新数据样本[24]。GAN 的网络结构主要由一个生成器神经网络和一个判别器神经网络组成(见图2)。
3.2 LSTM预测模型
长短时记忆神经网络是一种改进的循环神经网络,最初由Hochreiter和Schmidhuber[25]提出改进,因其独有的门控单元和隐藏状态,善于捕捉序列数据的前后依赖关系,至今已在多个序列预测场景[26-29]得到应用。LSTM的循环单元由3个控制门组成:输入门、输出门和遗忘门。它们分别决定了当前时刻所需保留的信息、下一时刻输出的信息和被遗忘的信息,从而改变当前的单元状态。

图2 GAN模型结构示意图Fig.2 Schematic structure of the GAN model
本部分利用网格搜索法对模型结构中的隐藏层神经元数量、丢弃概率、批量数、学习率等超参数进行寻优。试验发现当LSTM层数超过2层时,模型的预测精度开始明显下降,训练效率减慢,因此本研究选择LSTM层数为1层。最优超参数组合为:批量训练数600,学习率0.001,优化器选用Adam,激活函数为Rule,LSTM层神经元个数32,全连接层神经元个数8,丢弃神经元概率0.2。

图3 不同数据规模预测结果对比Fig.3 Prediction results in different data scales
3.3 试验设计
为了全面评价不同数据分布空间对模型预测结果的影响,本文分别利用GAN生成不同规模大小的新数据序列,进行如下5次试验:①使用60 000组原始数据集;②在原始数据集上增加GAN网络生成的10 000组数据;③在原始数据集上增加GAN网络生成的15 000组数据;④在原始数据集上增加GAN网络生成的20 000组数据;⑤在原始数据集上增加GAN网络生成的25 000组数据。
3.4 模型评价指标
试验评价指标选用常用的误差度量函数:平均绝对百分比误差(P)、均方根误差(R)、平均绝对误差(A)。同时本次试验在评价指标上额外增加模型运行时间,进行模型的运行效率对比。
(3)
(4)
(5)
式中:m为样本的总数量;yi为真实的井底压力值;ypre为预测的井底压力值。
3.5 结果分析
对比模型的预测结果(见图3)可以发现,未增加新数据训练的模型预测结果总体波动性较强;在井底压力维持稳定阶段,如6 300~6 400 m井段,预测结果与实测值存在较大偏差。相比而言,增加10 000和15 000组数据的预测模型在精度和稳定性上得到大幅提升,在压力的稳定阶段和突变处皆有快速响应性。其中增加10 000组数据的预测模型表现最优,P降低至0.043%,误差相比原来减小50%,A和R也相应降低。增加20 000和25 000组的模型误差显著上升(见图4),仅表现出对井底压力整体变化趋势的预测,未能有效分析局部压力变化,即过多增加生成数据会对模型的预测精度起反向作用。分析认为:①适量扩充数据集弥补了原有数据表征信息能力的不足,使得不同井段的数据分布更均匀。②增加的10 000组生成数据已有足够能力预测深层的井底压力,多余数据的增加无法表征更多有效信息,造成数据冗余,削弱了局部刻画压力变化的能力,使其预测精度降低。
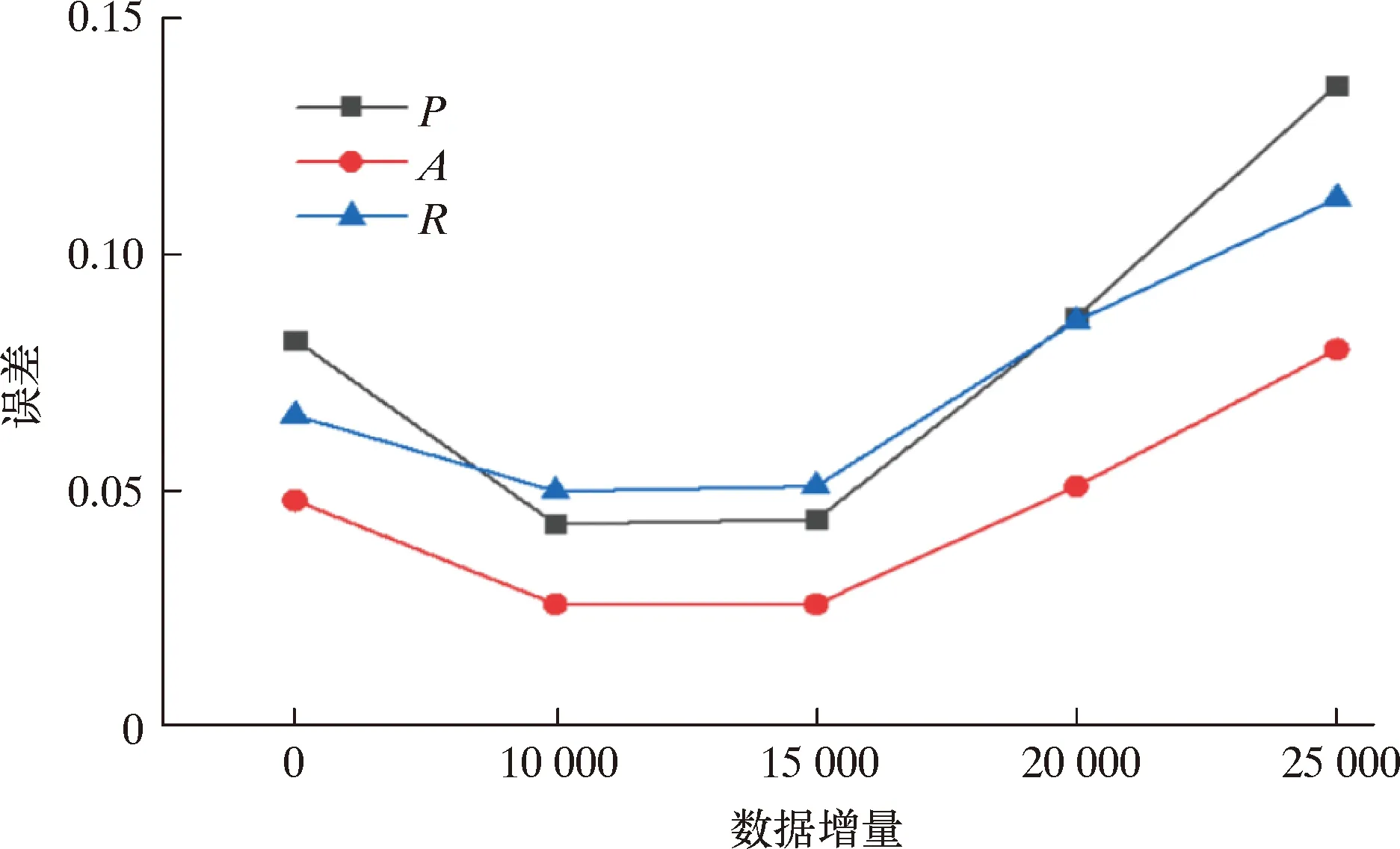
图4 预测结果误差曲线Fig.4 Errors of prediction results
通过可视化井深和井底压力数据分布(见图5)发现,GAN网络生成的数据有效扩充了不同井段间的井底压力。通过对比图5a和图5b,发现原有数据的井底压力分布较稀疏,使模型在更深井段处无法预测未知信息,这也是现有智能模型泛化能力低的根本原因。增加了10 000组新数据后的压力分布发生局部改变,使得模型在57.8~58.7 MPa的井底压力预测范围得到扩充。结合图3a和图3b可知,在6 300~6 400 m井段区间,新数据增强了预测模型对井底压力的表征能力,弥补了原有数据在该井段下的预测偏差。而增加15 000、20 000、25 000组数据后,井底压力的信息在57.8~58.7 MPa范围内得到进一步增强,使得模型更加注重压力的整体趋势变化,削弱了刻画局部压力变化的能力。图3d和图3e说明模型对于局部突变的压力变化分析能力不足,最终降低了预测精度。因此,基于本文的研究条件,扩充井段数据的15%~20%能够有效提升模型的预测精度。

图5 井深-井底压力数据分布图Fig.5 Data distribution of well depth-bottomhole pressure
4 增量更新集成式预测
4.1 模型整体设计流程
为了充分利用钻进过程中的实时数据流,实现动态更新井底压力预测模型,本部分提出一种基于迁移学习和集成学习的实时预测方法,整体的模型预测流程如图6所示。
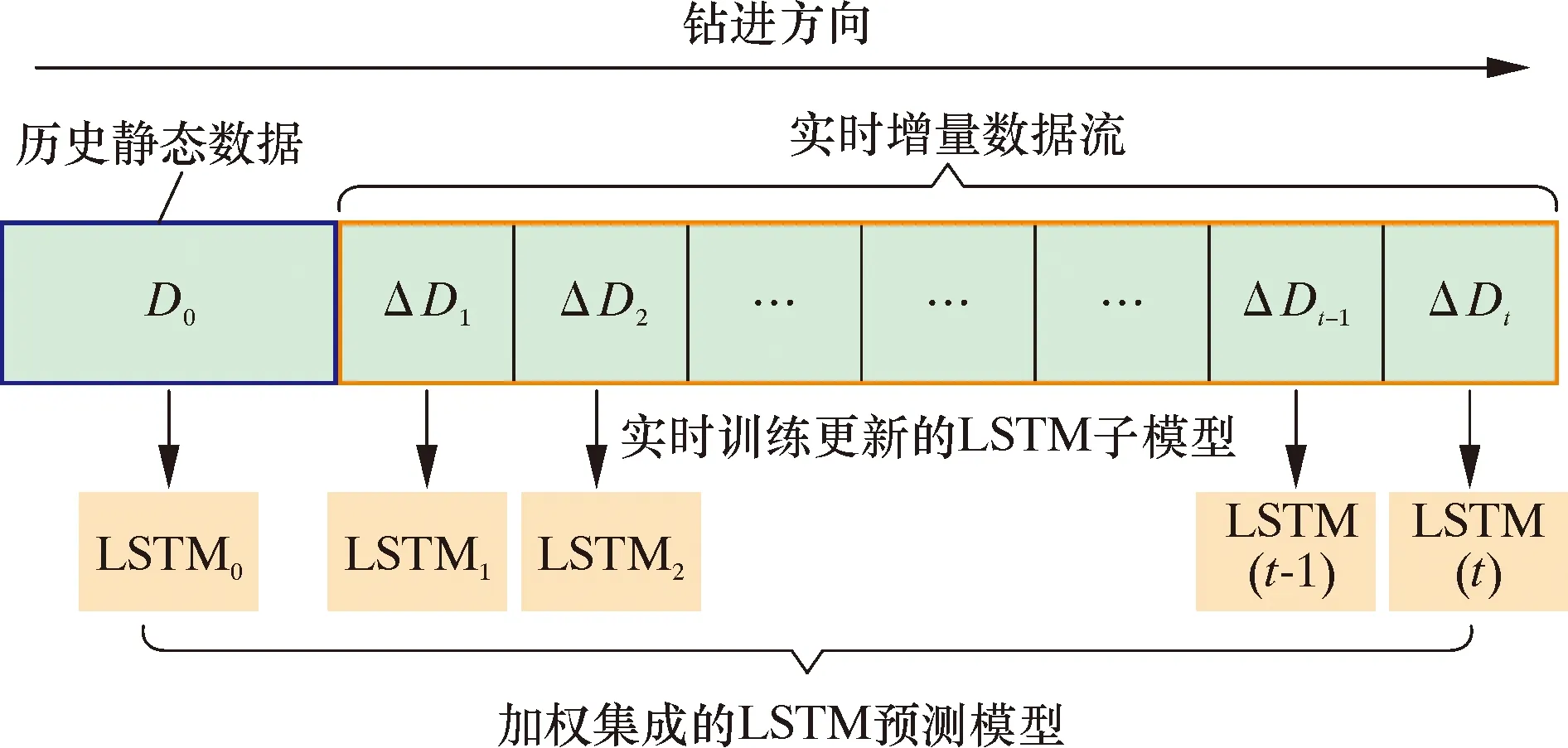
图6 实时增量更新的集成式LSTM模型预测流程Fig.6 Prediction workflow of the ensemble LSTM model with real-time incremental update
首先通过随钻测压数据的历史数据集D0训练得到子模型LSTM0;当获取增量数据ΔD1时,冻结LSTM0层权重,同时训练新的LSTM1层;输出信息的同时输入共享层S1融合(见图7),即融合了历史数据信息和增量数据信息,得到当前模型LSTM1。共享层加权输出可用式(6)表示。同样的,当获取增量数据ΔD2时,LSTM1进行迁移学习得到子模型LSTM2,如此循环使得子模型不断利用实时数据进行微调更新。最后将所有LSTM子模型进行误差加权集成,预测更深井段的井底压力。
(6)


图7 迁移学习的模型更新和特征融合示意图Fig.7 Model update and feature fusion of transfer learning
4.2 试验设计
为有效评价提出的增量更新模型,更加贴合现场钻进的实时场景,试验从原训练集中选取200 m上部连续井深序列,代表已钻和即将钻进地层训练集D0,ΔD1,…,ΔDt;100 m下部连续井深序列,代表未钻进地层测试集。根据数据流增量ΔD的不同,训练得到不同的LSTM预测子模型。最终集成不同子模型用于新井段的井底压力预测,并与历史数据训练的静态模型进行对比分析。
4.3 增量更新集成模型分析
4.3.1 更新增量区间选择
由试验评价结果(见表1)可以看出,使用增量实时数据训练的预测模型在精度和稳定性上皆优于使用全井段序列训练的预测模型,且模型的运行效率仅有细微差别,说明使用全井段历史数据训练的预测模型捕捉特定井段信息的能力不足,导致模型在新地层条件下的测试能力差,推广适用性受限。进一步研究发现,当增量更新的数据量达到30,即每采集30 m数据训练建立一个LSTM网络,其预测平均相对误差最低达到0.12%,此时集成的预测模型能够更好地融合历史与钻进信息,在更深井段具有更高的预测精度和稳定性。而增量更新数偏小或偏大时,由于数据有效信息不足或信息冗余,导致预测精度略有降低。
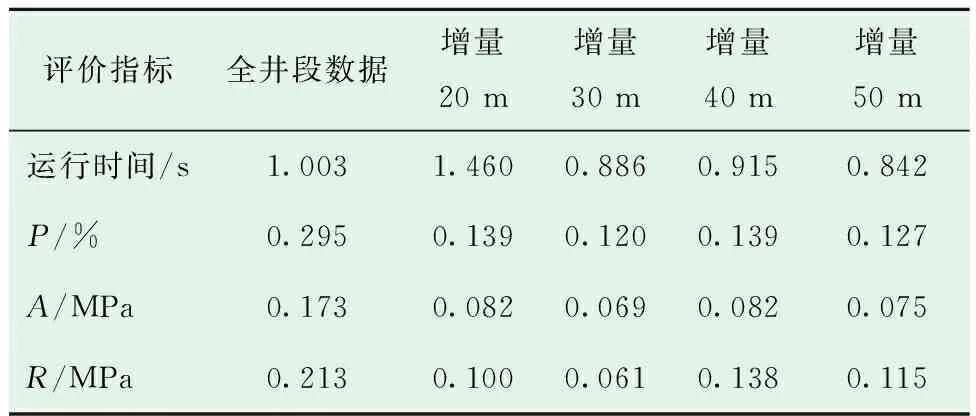
表1 模型评价结果Table 1 Model evaluation results
4.3.2 模型迁移共享的必要性
对比分析添加与未添加共享融合层的LSTM集成模型预测评价结果,如表2所示。由表2可知,添加共享层的模型预测精度更高,其中P较未添加模型下降30%。基于迁移共享层的预测模型不仅保留了上部地层的历史信息,同时融合了当前井段信息,使最终集成的预测模型能够精准预测更深井段的井底压力。对于智能模型迁移时效性问题,模型预测的难点在于同时处理历史静态信息和实时动态信息,因此信息的迁移融合尤为必要。

表2 集成模型的预测结果对比Table 2 Prediction results of ensemble models
5 可解释模型分析
5.1 混合注意力机制的LSTM模型
复杂模型由于嵌套复杂的非线性激活函数而面临着可解释性难的窘境。现阶段针对可解释的研究[30-31]多为对模型建立完成后的数据结果进行解释,很少有直接针对建模过程中的模型进行解释的研究。本部分通过修改原有LSTM模型内在结构,将注意力模块嵌入到模型结构中,提出了一种端到端的可解释模型(SI-LSTM),如图8所示,能够使模型对自身预测结果进行合理解释。

图8 混合注意力机制Fig.8 Hybrid attention mechanism
从修改标准LSTM模型的隐藏状态出发,使输入的每个参数都携带着自身的隐藏状态。在此基础上对每个输入参数的隐藏状态使用时序注意力机制,以获得每个参数丰富的历史时序信息。随后借助该历史信息,引入特征注意力机制进行历史信息的状态合并,将上述2步骤结合为一个概率混合模型[32],以帮助模型的学习、预测和自解释。从图8可以更清楚地了解混合注意力机制的工作流程,即每一个SI-LSTM处理当前时刻下的特征序列xt,最后再通过混合注意力加权将其进行合并。混合概率可以表示为:
(7)
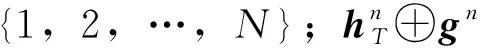
5.2 模型可解释分析
应用前述SI-LSTM可解释模型,本部分重点对模型的预测结果进行可解释分析。本文通过提取各输入特征的权重系数,便于将各个特征的重要性量化分析。可视化每一个训练周期的各个参数重要程度(见图9),发现当迭代次数为40时,各个特征的重要性程度趋向稳定,说明模型训练已经收敛。同时随着训练迭代进行,井底压力的特征重要性不断上升,说明模型逐步构建了上部测压数据与后续井底压力表现的联系。其余特征的重要系数变化趋势总体较平稳,取值范围从0.05至0.075。

图9 不同迭代时期的参数重要性Fig.9 Parameter importance at different iterations
图10显示了各个特征的重要性权重系数,发现SI-LSTM对井底压力自身的关注程度最高,对模型的预测过程贡献最大,系数达到0.25近似其他特征的5倍,即对预测结果的影响最大。现有的控压钻井方法主要包括[33]:①调节钻井液密度;②调节地面钻井液泵排量;③调节回压泵阀门形成一定的井口回压。此与本文重要程度排序较高的总池体积和钻井液密度相符。根据节流循环的井底压力计算公式为:
pwf=po+pm+pf
(8)
式中:pwf为井底压力,Pa;po为井口压力,Pa;pm为井筒流体液柱压力,Pa;pf为井筒流体流动损耗压力,Pa。

图10 各个参数的重要程度排序Fig.10 Ranking of parameters by importance
分析可知,总池体积的变化反映了井筒内流体体积的变化,钻井液密度会引起井筒流体的重力变化,两者是影响井筒流体液柱压力pm变化的重要因素,从而影响井底压力的变化。另外由于入口流量和出口流量对井底压力的影响存在关联性,所以当模型训练结束时,入口流量的重要性系数较于出口流量保持在更高水平。同时观察井底压力随采集时间变化的趋势(见图11)发现,从t-6时刻开始,即以当前时刻为节点的前6 s,井底压力的重要性开始凸显,且在t-4和t-3时刻达到峰值,说明前3~4 s的井底压力对当前时刻井底压力的预测贡献最大。

图11 井底压力随时间变化的重要程度Fig.11 Importance of BHP over time
综上所述,本文从特征和时序2方面分析得出:井底压力具有短期的自相关性,与控压钻井过程的井口回压传播形式相符。这表明压力的传播过程不是瞬态完成的,而是具有一定的传播速度和衰减性。该研究结果可一定程度上解释现场异常压力波动的原因,可为技术人员采取合理控压措施提供参考,对井底压力的高效调控具有借鉴意义。
6 结 论
针对复杂井段数据难以实时采集,智能模型难以适用不同井段以及模型的可解释性问题,本研究提出了基于GAN网络的数据拓展和增量更新的集成式井底压力预测方法,实现了时效性强、适用性广、精准度高的井底压力预测,并得出以下结论:
(1)在历史数据的基础上,能够拓展模型在未钻地层的观测数据空间,增强预测模型对井底压力局部突变的刻画能力,从而显著提高预测性能。结果表明,扩充15%~20%的GAN网络生成数据能提升模型的预测性能,但增加过度数据会导致模型误差增加,削弱捕捉压力动态变化的信息。
(2)基于增量更新的集成式预测方法,使模型能够动态捕捉压力变化信息,有效融合历史数据和实时数据,提取影响井底压力的共有特征,更快更好地适应井下复杂变化的环境,平均相对误差相比历史静态模型降低60%。
(3)利用基于混合注意力机制LSTM模型对预测结果进行合理解释分析,通过提取特征及时序的权重系数表征参数重要性,实现了结果的可解释。结果表明井底压力具有短期自相关性,与井口回压的调节相关。

