在综合实践活动中培养数据意识

邹敏慧

《掷一掷》是人教版数学五年级上册的教学内容，安排在“可能性”内容之后。教师应在教学中开展数据收集、整理与分析活动，让学生直观感知随机现象中的可能性与规律性，发展数据意识。

一、依托试验体会事件的随机性

小学生对于真实发生的事情感悟更深刻，更容易理解确定性事件；对于不确定现象，则可能存在认知偏差。因而，教师需要借助直观方式帮助学生建立数学概念。

《掷一掷》这节课中，笔者设计了一个游戏情境：将两个骰子的点数和分为两组，掷出5、6、7、8、9的点数和则教师赢，掷出2、3、4、10、11、12的点数和则学生赢。课堂上，大多数学生认为教师只有5个点数和，而学生有6个点数和，所以学生赢的可能性大。笔者提议让学生掷骰子试一试，在2分钟时间内，师生轮流掷骰子，记录各点数和出现的次数，对比师生赢的次数。通过实际操作，学生发现教师赢的次数明显偏多，即教师赢的可能性大。一组组真实数据让学生感受到自己的猜想可能是不对的。但是，在5个班的教学实践中，有2个班出现个别小组的数据是学生赢的次数多的情况。笔者将这样的数据呈现出来，利用特殊数据，引导学生感知事件的随机性，即虽然大多数小组是教师赢的次数多，但并不代表所有小组一定会出现教师赢的次数多的情况，也有可能出现学生赢的次数多的情况。数据的冲突，激发了学生的探究欲望，为接下来数据的深入分析埋下伏笔。

二、利用动态统计图直观刻画数据

小学生客观分析随机现象的能力较弱，他们需要借助足够的数据证据来理解随机现象。条形统计图可以集中呈现各小组的数据，且直条的高低能直观刻画数据信息，使数据之间的差异清晰可见。

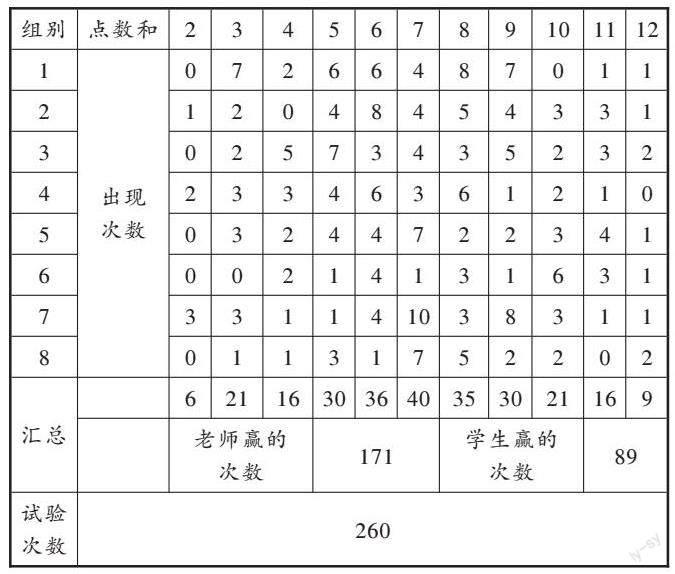
为了让学生真实经历数据统计的过程，清晰地看到数据的变化，笔者随机选取8个小组的试验数据，让学生代表整理这8个小组的数据（见下表）。

随着一个个数据输入电脑，生成的条形统计图中的直条在经历了起伏不定的变化后，逐步趋向缓慢累加的动态，最后高低不同的直条呈现出“金字塔”状（如图1）。大幅度变化后的缓慢跳动仿佛在告诉学生，每个点数和的变化趋势不会再大起大落，数据的稳定性在量的增加中悄然呈现。

这样的体验过程让学生对数据变化的感悟十分深刻。学生通过现场整理数据、形成条形统计图的过程，直接从图表中读出信息：点数和“7”出现的可能性最大，每个点数和出现的可能性不都相等，教师赢的次数远多于学生赢的次数，等等。条形统计图中直条高低的不同进一步引发了学生的思考：5个点数和并不意味着两颗骰子只能掷出5种可能的情况，而是暗藏着更多骰子点数的组合。这样，教学自然进入到对比分析、深究原理的环节。

三、借助对比联系发现数据规律

要想真正读懂数据，教师还要在数据对比中分析、归纳、总结数据的规律性，深化学生对数据随机性的感悟。

有了前面两个活动，学生从试验数据中看到教师赢的可能性大，想要寻找原因。教学中，笔者引导学生思考“同时掷两颗骰子，什么情况下会出现点数和为‘2’呢？”，并让学生依次列举各个点数和的骰子点数的组合。经过整理和分析，学生敏锐地发现每个点数和出现的可能性与两个骰子点数的组合密切相关，出现点数和“7”的组合有“1+6、2+5、3+4、4+3、5+2、6+1”6种情况，而点数和“2”与“12”均只有1种，点数和“3”与“11”各有2种……最后，学生总结得出：11个点数和可能的组合数也呈“金字塔”状分布，与前面条形统计图的呈现恰好呼应，强化了学生对数据规律的理解和記忆。

接下来，笔者安排学生再次拿出自己小组的试验数据，进行对比观察与分析。学生发现，自己小组的数据并没有显示出点数和“7”出现的次数最多，甚至大多数点数和出现的次数都与理论分析有偏差。

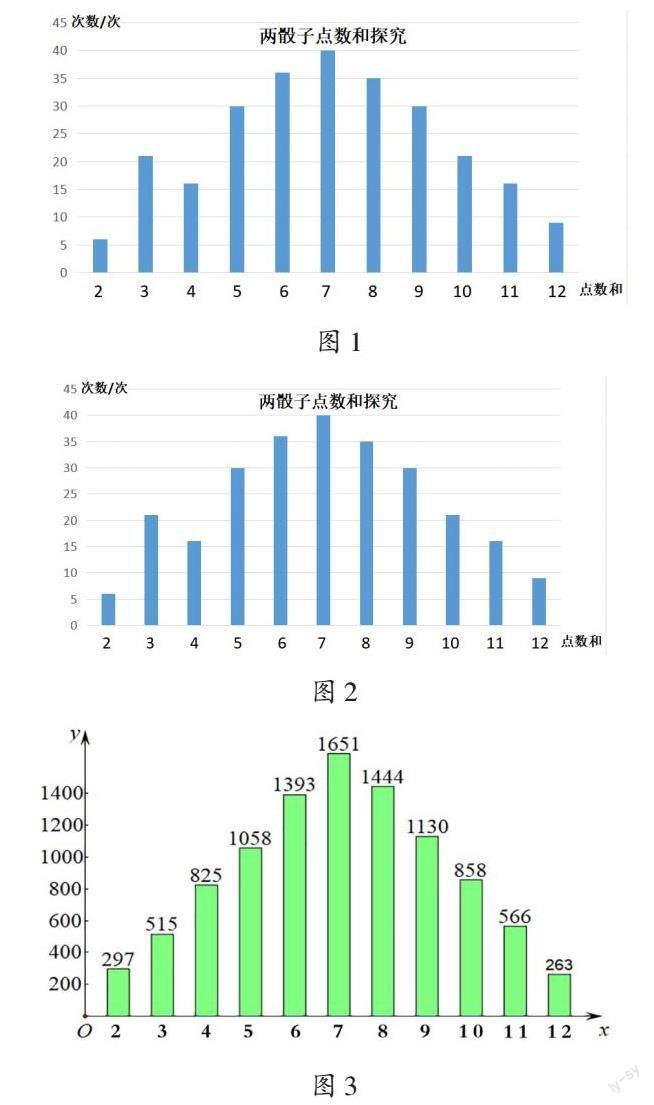
基于此，笔者引导学生汇总8个小组的数据，这样得出的11个点数和出现的次数与理论分析就十分接近了（如图2）。

这次对比让学生对“掷骰子过程中，只要有足够的数据就会呈现出规律”这个教学难点有了初步感悟。笔者继续利用几何画板模拟程序增加试验次数，显示试验10000次后11个点数和出现的次数。学生发现增加试验次数后，结果与理论分析的“金字塔”状十分吻合（如图3）。

从试验到分析原因，从1个小组几十个数据到8个小组几百个数据再到模拟10000次试验后的数据，对比之下，学生看到点数和出现的次数随着数据量的增加，其变化趋势与理论分析趋于一致，呈现出明显的规律性。这样对比，学生深刻感悟到数据的量推动随机现象由不确定性走向规律性。

（本文系湖北省教育学会“十四五”教育科学研究课题“小学数学跨学科综合与实践课程研究与实践”研究成果。）

（作者单位：咸宁实验外国语学校）