破解“心灵感应”

洪昊阳

数学活动课上，张老师为我们表演了“心灵感应——猜点数”的魔术。只见张老师背对着我们，她让陆相丞把4个骰子翻来覆去打乱后，像叠罗汉一样竖直垒起来。一切准备就绪，张老师回转身来，瞟了一眼骰子，然后迅速在黑板上写下一个数：24。她说：“上面看到的面不算（最上面的点数是4），4个骰子所有能看到的面不算，看不到的那些面的点数之和是24。”大家听了将信将疑。陆相丞将骰子一一拿下，嘴里不停地口算：“3+2=5，5+5=10，10+5=15，15+2=17，17+4=21，21+3=24。”呀，神了，的确是24！

难道张老师真有“心灵感应”？

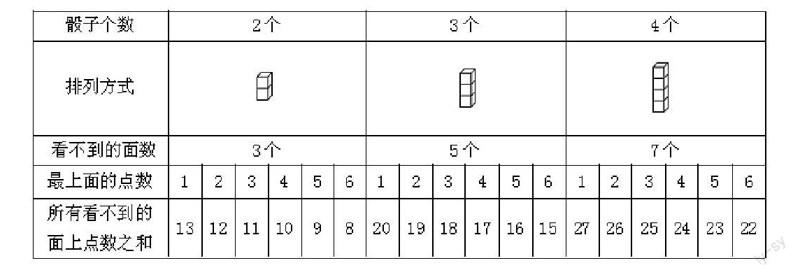
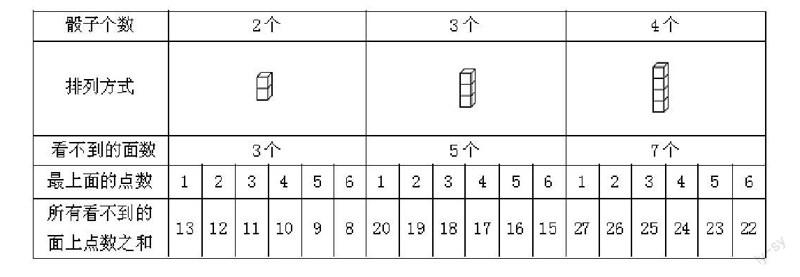
下课后，我向同学借了几个骰子，分别列出了2、3、4个骰子垒起来的情况。

经过认真观察后我发现：正方体的骰子都有6个面，6个面上的点数分别是1、2、3、4、5、6，总点数之和为21；每个骰子中相对面上的点数分别是1和6、2和5、3和4，即相对面上的两个点数之和为7。如果有4个骰子，总点数为21？，所有能看到的面上的点数之和为：7？？+最上面的点数。张老师的魔术中最上面的点数是4，因此，所有看不到的面上的点数之和为：21？-（7？？+4）=24。哇，原来要想知道所有看不到的面上的点数之和是多少，关键在于最上面的点数！

回到家后，我把这个发现告诉了爸爸。爸爸表扬了我，说：“儿子，爱动脑筋就是好样的。其实，这个规律还可以更简单一些。你看，看不到的面一定是上面或下面……”爸爸的提醒使我豁然开朗。将两个相对面看成一组，有2个骰子时，看不到的面上的点数=2组点数之和-最上面的点数；有3个骰子时，看不到的面上的点数=3组点数之和-最上面的点数；有4个骰子时，看不到的面上的点数=4组点数之和-最上面的点数……所以，所有看不到的面上的点数之和=7作蛔痈鍪钌厦娴牡闶？

太棒了，我终于破解了张老师的“心灵感应”！