大括号的妙用

贺珊

“总量=分量+分量”是第一学段涉及的主要数量关系。人教版数学一年级上册教材在编排了6和7的认识及加减法后，编排了“运用大括号解决问题”的内容，帮助学生直观理解总数与部分的关系，初步建立加、减数量关系的模型。如何在后续教学中延用画大括号解决问题的策略？

利用大括号建构部分与总数的关系。用大括号再现信息和问题，能将题目文字的内涵进一步抽象，把表示总数与表示部分的数量在大括号上一一对应地呈现，帮助学生理解加减问题的一体性和加减运算的互逆性。

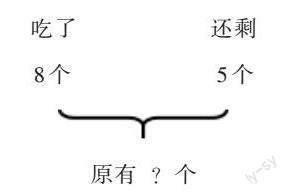
例如，解决“我吃了8个水饺，还剩5个。原来有多少个水饺？”问题时，常常有学生错误地列减法算式“13－8=5”解决问题。这是学生思维固化的体现，如看到“吃了”就用减法表示“去掉”，看到“剩下的”就要放在算式的等号后面等。事实上，学生所理解的等量关系没有错。如何引导这部分学生直接用已知信息求未知呢？笔者引导学生画大括号表征题目中的数量关系（如下图）。

图示可以清晰地呈现：水饺分成两个已知的部分，即吃了的和剩下的；把这两个部分用加法合起来，就是原来水饺的总数。学生画大括号的过程相当于把题目去情境化的过程，有利于学生借助图形直观抽象出题目中的数量关系。

后续，学生解决形如“我们已经做了25朵粉花，还要做10朵粉花。一共要做多少朵粉花？如果再做40朵黄花，黄花和粉花一共要做多少朵？”的问题时，就能自觉画大括号理解题目中的数量关系（如下图），从而正确解题。

学生将两个大括号整合在一起，凸显了两个问题之间的联系，即第一个问题求的粉花总数是第二个问题花朵总数的一个部分。

利用大括号贯通一题多解。在学习连加、连减运算时，教师引导学生用画大括号的策略解题，可以使学生对一题多解形成贯通性理解。

例如，解决“有10个五角星，先剪掉2个，再剪掉3个。还剩几个五角星？”问题时，学生通过“先剪掉”“再剪掉”的语境，很容易列出连减算式“10-2-3=5”解决问题。如果教师引导学生画大括号分析数量关系（如下图），学生就能直观地发现：无论从总数中去掉哪两个部分，都能得到第三个部分；剪掉一个部分后，得到的就是另外两个部分的和，进而可列算式“10-2=8；8-3=5”解决问题；利用大括号明确“2+3”表示两个部分的和，就能列算式“10-（2+3）=5”解决问题。

学生根据题意判断出总量与部分量、畫出大括号并在相应位置标注信息的过程，相当于建立了情境问题解决的通用模型，有利于学生发展数学眼光和数学思维。

（作者单位：华中科技大学同济医学院附属小学）

责任编辑  刘佳