融会贯通深入本质

刘向权 刘子岭

摘要：通过两道经典的“姊妹习题”的教学，从系统的角度审视数学，置散乱知识于系统之中，着眼于数学知识间的紧密联系和内在规律，以及数学思想方法的渗透，在融会贯通的过程中，透过纷繁复杂的现象，深入数学的本质。

关键词：习题教学 联系规律 思想渗透

《义务教育数学课程标准（2022年版）》（以下简称《新课标》）在“课程实施”之“教学建议”部分明确指出：教学内容是落实教学目标、发展学生核心素养的载体。在教学中要重视对教学内容的整体分析，帮助学生建立能体现数学学科本质、对未来学习有支撑意义的结构化的数学知识体系。基于上述观点，怀揣着对数学教研孜孜不倦的热情，笔者对沪科版八年级上册数学教材中两道“姊妹习题”进行了认真挖掘与剖析，并尝试在融会贯通中深入并揭露数学的本质。本文将这两道习题的教学设想、教学实施和教学思考对读者加以分享，旨在为广大初中數学教育同行提供教学参考，以求抛砖引玉。

一、习题呈现

习题1：已知，如图1，AB∥A′B′，BC∥B′C′，BC交A′B′于点D。

求证：∠B=∠B′。

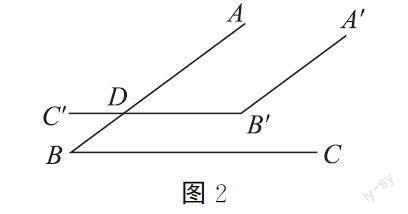
习题2：已知，如图2，AB∥A′B′，BC∥B′C′，B′C′交AB于点D。

求证：∠B+∠B′=180°。

这两道习题源自沪科版八年级上册数学教材第85页第13章第2节“命题与证明”节末习题13.2中第7题、第8题。为便于叙述，本文分别将第7题、第8题称为“习题1”“习题2”。因这两道习题在教材中连续出现且关系特殊，可共同抽象、归纳得到一个重要数学命题，故称它们为“姊妹习题”。

二、教学设想

“命题与证明”是初中生正式学习几何证明的起始章节，通过翻阅沪科版八年级上册数学教材可以发现，本节教材的教学内容约需5个课时完成，而整节教材仅安排了9道习题，足见题目数量之少。因此，如何才能最大限度地发挥每道习题的教学价值与效益，无疑是对数学教师教学智慧的一大考验。读者若能细细品味习题1、习题2的编排顺序与逻辑关系，教材编写者的深刻意图和巧妙设想便可见一斑。在本节两道“姊妹习题”的教学中，如果仅停留在“完成证明”的肤浅层面，这无异于坐失良机。基于此，笔者试图依托两道“姊妹习题”的教学，引导学生纵深挖掘数学知识之间的微妙联系和内在规律，进而将散乱的数学知识系统化，让学生在融会贯通中，透过纷繁复杂的外在现象，认识事物的内在本质，进而领悟数学的真谛。

三、教学实施

（一）引导分析，证明习题

教师：请同学们结合习题1的条件和图1进行思考，这两个角离得比较“远”，要证明∠B=∠B′，该怎么办呢？

学生1：可以利用平行线的性质，先证明∠B和∠B′都等于∠A′DC（或∠BDB′）。

教师：具体说说怎么书写证明过程吧！

学生1选择利用“两直线平行，同位角相等”这一性质（在实际教学中，也可能会有同学选择利用“两直线平行，内错角相等”这一性质）口述证明过程，其余同学补充如下：

证明∵AB∥A′B′，BC∥B′C′，（已知）

∴∠B=∠A′DC，∠B′=∠A′DC。（两直线平行，同位角相等）

∴∠B=∠B′。（等量代换）

教师：在这里，∠A′DC就像一座“桥”，建立了∠B和∠B′之间的联系，这个思路很巧妙！我们接着分析习题2，哪位同学来谈谈自己的想法？

学生2：这道题也可以类似地通过∠ADB′这座“桥”将∠B与∠B′联系起来。

教师：请说说具体怎样联系。

学生2：利用平行线的性质，先证∠ADB′+∠B′=180°，再由“两直线平行，同位角相等”可证∠B=∠ADB′，从而得到∠B+∠B′=180°这一结论。

此题可先让学生尝试证明，再逐步规范证明过程，具体如下：

证明∵AB∥A′B′，（已知）

∴∠ADB′+∠B′=180°。（两直线平行，同旁内角互补）

∵BC∥B′C′，（已知）

∴∠B=∠ADB′。（两直线平行，同位角相等）

∴∠B+∠B′=180°。（等量代换）

教师要善于鼓励学生从不同角度分析问题，尝试用不同方法解决问题，只要思路清晰合理，方法得当，均应予以肯定。

（二）自然联想，整合归纳

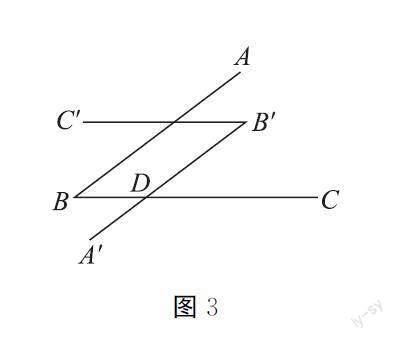
教师：对于习题1，在不改变题目条件的前提下，如果教材未给出图形，你能通过联想，画出与图1不同的图形吗？

学生3与同学充分交流讨论，结合图1联想得到图3。

教师：那么，对于习题2，如果将题目中的“B′C′交AB于点D”改为“BC交A′B′于点D”，其他条件和所要证明的结论不变，你还能画出与图2不同的图形吗？

学生4先自主尝试画图，再与同学进行必要的交流讨论，联系图2得出图4。

在引导学生尝试画出图3、图4时，个别同学可能只是简单地将图1、图2中的∠B′平移，便误以为得到了新图形，若遇此情况，教师需引导学生对前后所画图形加以比较分析，在不挫伤学生积极性的前提下予以明确否定，以免对其他同学造成误导。

教师：接下来，我们能不能想办法将上面四个图形整合成一个图形呢？

经学生交流讨论后画出草图，教师引导学生对草图进行适当调整，做出标注得到图5。

教师：结合整合后的图5及习题1、习题2的证明，你能尝试着归纳出结论吗？

学生5：如果两角的两边分别互相平行，那么这两个角相等或互补。

学生的语言未必简洁精炼，教师应注意引导学生对语言进行梳理和推敲。

（三）梳理升华，发掘联系

教师：但是，两角何时相等，何时互补呢？

此时，若学生感到有难度，可审时度势引导学生从“两组平行边的射线方向”这一角度进行思考分析。

学生6：当两组平行边的射线方向全部相同（图5中∠B和∠1）或全部相反（图5中∠B和∠3）时，这两个角相等。

学生7：当两组平行边的射线方向一同一反（图5中∠B和∠2，∠B和∠4）时，这两个角互补。

学生6和学生7的回答未必如此准确精练，只要大意正确，再加以引导和完善，师生便可逐步达成共识。

教师：如果我们将两组平行边射线方向相同的关系规定为“正”，方向相反的关系规定为“负”，进而将两角相等的关系规定为“正”，互补的关系规定为“负”，那么，刚才两位同学梳理总结出的结论，可以怎样描述呢？

学生8：“正、正”得“正”，“负、负”得“正”，“正、负”得“负”，“负、正”得“负”。

教师：还能描述得更简洁一些吗？

学生8（回顾并联系有理数乘、除法法则，与同伴进行深入交流讨论后回答）：“同号”得“正”，“异号”得“负”。

教师：原来，这和有理数乘、除法的符号法则竟然有如此微妙的联系！

（四）平移直线，深化联系

教师：如果我们试着平移图5中的直线EF，使它与射线BA所在的直线重合，得到图6。大家对这个图形熟悉吗？

学生9：在七年级下册第10章学习“平行线的性质”时，经常见到与图6类似的图形。

教师：你说得很好，也很具体！由于在图6中仍然有∠ABC=∠1，∠ABC=∠3，∠ABC+∠4=180°，因此上述关系分别是对“两直线平行（GH∥BC），同位角相等（∠ABC=∠1）”、“两直线平行（GH∥BC），内错角相等（∠ABC=∠3）”和“两直线平行（GH∥BC），同旁内角互补（∠ABC+∠4=180°）”这几个性质的生动诠释。

学生恍然大悟，用目光相互交流，思维得到碰撞，并向纵深发展。

教师：在图6的基础上，如果我们再将直线GH平移，使其与射线BC所在的直线重合，得到图7。这个图中又蕴含了哪些我们熟悉的数学知识呢？

学生10：两角相等的定义。

学生11：平角的定义。

學生12：（邻）补角的定义。

学生13：对顶角相等。

学生的回答未必如此全面、有序，也可能会有变化，必要时需稍作引导，逐步完善，进而达成共识。

教师：由此看来，数学知识之间的联系，有时竟如此让人意想不到，却又那么合情合理。

至此，数学知识之间的联系又得到深化，学生的心灵被彻底震撼，他们已深深折服于数学的无穷魅力。

（五）透过现象，揭露本质

教师：从对两道“姊妹习题”的证明开始，一路走来，摸爬滚打，我们发现两角相等的定义、平角的定义、（邻）补角的定义、对顶角相等、平行线的性质这些看似散乱的数学知识原来包括在同一个结论（如果两角的两边分别互相平行，那么这两个角相等或互补）之中。或者说，它们原本就属于同一个系统。由此可见，要学好数学，我们就应该善于透过现象……

学生：（齐答）看本质！

教师总结点题，在帮助学生简化记忆数学结论、自主建构数学知识体系的同时，数学课堂也得到了升华，彰显至高的教学境界。

四、教学思考

（一）从解决问题到问题解决

解题教学的最低境界是“为解题而解题”，解完一道再来一道，下课了，一节课自然也就结束了——这是低效甚至无效的解题教学，显然没有真正解决问题，更没有实现问题解决。解题教学要引导学生“从最近联想到优化思维，从优化思维到借题发挥，从借题发挥到解决问题，从解决问题到问题解决”这样一个螺旋生长的思维链中去进行解题训练。本节课，就两道“姊妹习题”的教学而言，若仅以学生会证明两道习题为目标，教学效率固然会显得很高，但教学效果则会大打折扣，教学效益也远未得到深入挖掘；若教师顺势引导学生由图1、图2分别联想到图3、图4，通过整合图形优化思维，并借题发挥总结结论，再举一反三运用结论，基本上就能算作解决问题了；而如果能在解决问题的基础上，努力发掘数学知识之间的内在联系，并将微妙的联系逐步引向纵深，进而将看似散乱的知识纳入同一个系统中，便能称得上问题解决了。

（二）从知识碎片到结构体系

例题教学唯有立足当下，承前启后，一以贯之，既有必要的纵向延伸，又有适当的横向拓展，学生的数学知识才能获得自然生长。例题教学是这样，习题教学也是如此。笔者以为，对于上述两道“姊妹习题”的教学，大致可分为以下3个层次（或3种教学境界）。层次1：教师带领学生依次完成两道习题的证明后，再对证明思路和方法做简评或互评。层次2：在完成两道习题证明后，教师进一步启发学生思考：这两道习题之间有何内在联系？通过习题证明，你能归纳出一个怎样的数学结论？层次3：在习题证明、点评完毕后，教师先引导学生抽象归纳数学结论，再进一步鼓励学生展开适当联想，启发、引导他们对习题1、习题2的原图（前文中的图1、图2）加以变换、整合，从而建立起“两角相等”“平角”“（邻）补角”“对顶角”“平行线的性质”这些数学知识之间的联系，构建完整的数学知识体系，揭示数学的内在规律与本质。

显然，教学层次1充其量只算完成了习题证明，仅停留在单纯利用“平行线的性质”这一知识点解决数学问题的层面，数学知识无疑被严重碎片化了。而从教学层次2到数学层次3，则逐步揭示了数学知识之间的联系，实现了前后贯通。纵观这3个不同的教学层次，还会发现，数学知识已实现由“点”到“线”、由“线”到“面”的飞跃，碎片化的数学知识已逐渐形成严谨的结构体系。

（三）从观察现象到深入本质

因图1和图2中都有“两角相等”“平角”“（邻）补角”“对顶角”“平行线性质”的“影子”，且在证明两道“姊妹习题”时主要用到了这些数学知识，而这些数学知识又分散在沪科版七年级数学教材上、下册不同的章节中。故教师引导学生完成习题证明后，顺便带领学生复习回顾这些知识内容，这一做法不仅有用而且很有必要。但问题是，如果教师走马观花式地带领学生将这些数学知识“过一遍”，这样的处理方式不仅过于肤浅、粗糙，数学课堂也会显得索然无味。其实，只有教师真正做到了对数学知识方法的高位理解，才能让学生体会到数学知识之间的联系，运用数学的思维方式进行思考，增强学生发现和提出问题的能力、分析和解决问题的能力。在此前提下，教师与学生一起将相关数学知识“理一遍”，便能拨开笼罩在数学课堂上的“团团迷雾”，化“观察现象”为“深入本质”。

参考文献：

[1]中华人民共和国教育部.义务教育数学课程标准（2022年版）[M].北京：北京师范大学出版社，2022.

[2]卜以楼.生长数学：卜以楼初中数学教学主张[M].西安：陕西师范大学出版总社，2018.

[3]刘向权.承前启后一以贯之[J].中学数学教学参考（中旬），2020（5）：4345.

责任编辑：唐丹丹