高中数学函数教学中渗透数学思想方法的研究

袁波

摘 要：函数是贯穿于高中阶段数学学习始终的重要知识点，也是难点。如何让学生更好更深刻理解函数，一直以来都是高中数学教学所探讨研究的问题。在新课改背景下，数形结合思想被广泛应用，它已经成为函数教学中不可或缺的数学方法之一。本文就提出函数教学中数形结合的教学原则和渗透策略，并配合实例说明。

关键词：高中数学函数；数形结合；思想渗透；教学；原则；方法策略

所谓数学思想就是对数学理论与数学事实的本质认识及融合，它具有高度的抽象性与整合概括性。可以说，数学概念体现数学思想，数学思想概括数学概念，二者相辅相成。有学者就认为，数学思想就是一种理性认识，它是对数学知识及方法的本质阐述，属于基于数学规律阐述的理性认知范畴。在高中函数教学中，教师应该渗透更多数学思想，而不是单纯教学数学方法，这对学生更深层次掌握并灵活运用函数知识非常重要。

一、关于“数形结合”的应用原则

数形结合拥有自己独立的思考体系，它除遵循最基本的数学教学思想原则外，还遵循以下两点原则：首先就是等价性原则，它表示数的代数性质应该与形之间形成几何直观间转化，二者应该呈现等价关系，换言之问题中所反映的数与形必须拥有一致性。举例来说：问在方程[x13=2sinx]中有多少个实根？在做该题目前学生需要制作函数[y=x13、y=2sinx]的函数图，由于两个函数都属于奇函数，所以学生只需要做[x≥0]的函数图部分即可。这就是数形结合思想渗透给学生的学习意识，学生必须明确函数学习中各个函数的基本性质、特征，然后根据题目所提出的条件来作出回应，节省解题时间，这也是对学生函数基础知识的一次考察，是对等价性原则的最好诠释。

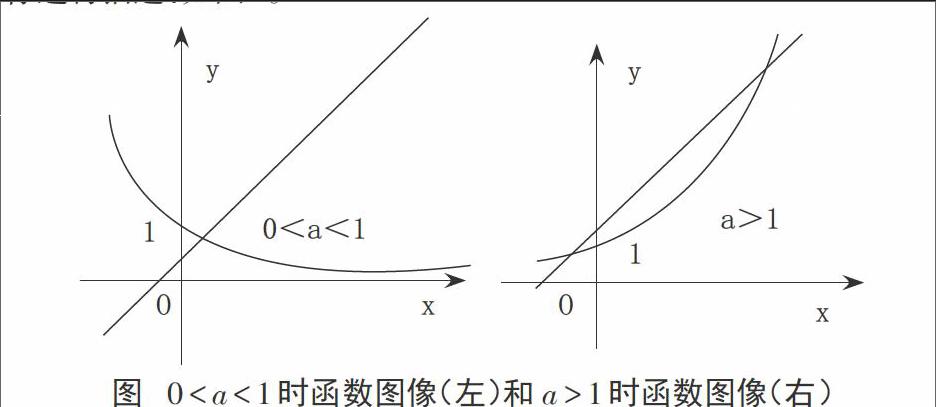
其次是简单性原则，它代表了学生所必须学会的数形转换能力，即学生在转换函数曲线与数学方程时要尽量让几何图形清晰美观，而让代数计算更加简单明了。再举例来说，假如有函数[fx=ax-x-a（a>0且a≠1）]，函数中有两个零点，求a的取值范围。

该题目在解答时应该给出条件[gx=ax（a>0且a≠1）hx=x+a]，然后给出[a>1]和[0

[O][x][y][1][01]

图 [01]时函数图像（右）

由于函数方程中具有两个零点，所以这就说明在函数[gx、hx]中就有对应的两个不同交点。从对图1的观察中可以发现，当[a>1]时是符合题目要求的，所以实数[a]的取值范围应该是[a>1]。

通过对此题的解析可以发现，自变量x应该在指数位置，如果运用一般代数方法可能无法解题，如果采用数形结合思想解题，就可以将题目简单化，将抽象的代数形式转化为直观的函数曲线图形，这就遵循了数形结合所倡导的简单性原则，利用几何图形解释了函数代数运算中的深刻规律。

二、在高中函数数学教学中渗透数形结合思想的教学策略

函数教学具有一定复杂性和系统性，利用数形结合思想渗透方法是希望将教学过程简易化，进而加深学生对学习内容及过程的认识，体现数形结合渗透思想的有效性。为此，本文希望给出两点教学策略，希望帮助高中生更好学习函数知识。

（一）强化高中数学函数的多种表征方式与转换

传统高中函数教学中，数与形的教学学习过程与理解过程都是分开的，并没有实现有机结合，但实际上其教学过程中是存在函数文字、图形及符号的三语言转换过程的。因此如果仅以概念中的数形分离理解来教导学生必然会让他们对函数性质及解题方法产生歧义，难以深刻并全面理解知识内涵。基于此就必须帮助学生真正掌握有关函数的基本性质，特别是培养他们实现函数中3种语言有效转换的解题能力。举例来说，在“函数的单调性”一课教学过程中，教师就可以首先提出定义“如果对于区间I内的任意两个函数值[y1、y2]，当[y1

（二）重视函数模型之于教学的重要作用

如何将函数知识留在学生脑海里，教师可以采用函数模型来实现这一教学思路，这也是一种典型的数形结合方法。为学生树立模型概念，一方面可以将函数中许多抽象的思维概念具象化，一方面也能帮助学生记住函数模型，让他们每当解题时就将模型与题目联系起来，形成良好的解题思路，例如从几何直观角度来把握函数，激发学生对函数学习的兴趣，同时也鼓励学生自己画简单的函数模型，将数形结合思想切实反映到函数学习当中，观察函数的变化过程。

比如说，高中所学习的“双勾函数”[y=x+ax]中，许多学生都不知道该函数的来历，此时教师可以引导学生画出[y=x+1x]函数的图像，再配合几何直观角度来理解该函数，最后研究双勾函数的相关图像。另外，也可以根据圖像观察来让学生明白双勾函数的基本变化状况与性质，再引导他们通过代数角度来验证函数。如此方法教学可以让学生深刻记住双勾函数及其它的函数模型，进而逐步实现对函数本质的深层次理解，在潜移默化中培养学生数形结合的能力，也体现了渗透数学思想对于高中函数教学的重要性。

三、总结

本文简单描述了有关高中数学函数教学中的数形结合数学思想渗透方法，并阐述了它对于提高函数教学质量的重要作用。作为教师应该明确突出“数形对应、数形转化以及数形分工”在教学过程中的应用和衔接过程，以全局着眼来提高函数教学层次水平，为学生深层次理解函数知识提供了优良条件。

参考文献：

[1]宫凡玉.高中数学教学中渗透数形结合思想的研究[D].鲁东大学，2015.

[2]李源.数形结合思想方法在高中函数教学中的有效渗透与应用[D].扬州大学，2014.