基于非平稳非高斯随机振动的航天结构疲劳寿命分析

张鹏飞，丁镇军，陈贵龄，吴家驹

基于非平稳非高斯随机振动的航天结构疲劳寿命分析

张鹏飞，丁镇军，陈贵龄，吴家驹

（北京强度环境研究所，北京，100076）

随机振动试验是考核结构疲劳强度的常用方法，通常假定振动信号符合高斯分布。实际使用中存在非平稳非高斯随机振动环境，非平稳非高斯振动中的结构疲劳寿命分析有助于试验技术的提高。通过介绍非平稳非高斯随机振动的特征和生成方法，分析了跌宕周期对非平稳非高斯信号时域波形的影响。建立典型试件的有限元模型，按照波形再现振动试验的加载方法和时域疲劳寿命分析方法，研究了峭度和跌宕周期对疲劳寿命的影响。结果表明峭度和跌宕周期对疲劳寿命有显著的影响。研究结果对于提高环境试验真实度、改善疲劳寿命试验技术具有参考意义。

非平稳；非高斯；疲劳寿命；跌宕周期

0 引 言

结构振动疲劳是指结构所受动态交变载荷的频率分布与结构固有频率接近时，结构共振所导致的疲劳破坏现象[1]。结构的疲劳寿命主要取决于关键部位的应力响应幅值。在实验室中，经常使用随机振动试验方法来考核产品的疲劳强度，认为随机振动更符合实际使用环境。对于大多数的随机振动试验，通常假定振动输入和应力响应符合高斯分布，然而，实际上结构会经历非高斯随机振动环境，并导致响应也是非高斯的。文献[2]研究了典型的非高斯随机振动时间历程，非高斯随机振动发生在火箭起飞和跨声速段、压力震荡、车辆道路运输、非线性系统的振动等环境中。非高斯振动相对于高斯振动，出现高峰值的概率更大，这种差别可以导致完全不同的累积疲劳损伤。

非高斯随机振动包含两种类型，即均方根不随时间变化的平稳非高斯和均方根随时间变化的非平稳非高斯[3]。大部分对于非高斯振动环境和疲劳寿命影响的研究仅限于平稳非高斯[4-5]。机械结构的动强度试验结果表明，虽然两种非高斯激励有相同的功率谱和峭度，但是非平稳非高斯振动所造成的累积损伤比平稳非高斯振动所造成的累积损伤严重。文献[6]使用典型结构件的算例对比分析了高斯振动、平稳非高斯振动和非平稳非高斯振动的疲劳寿命，指出非平稳非高斯振动对结构的累积损伤最严重，但没有探讨非平稳非高斯振动对疲劳寿命的影响规律。文献[7]提出在表征非平稳非高斯随机振动时引入跌宕周期的概念，并评估了考虑跌宕周期的非平稳非高斯信号对疲劳损伤的影响，但认为峭度和跌宕周期对累积损伤的影响规律还需要进一步确认。

本文是对上述工作做进一步研究和验证，介绍了非平稳非高斯信号的特征和生成方法，分析了跌宕周期对非平稳非高斯信号时域波形的影响，建立了典型试件的有限元模型，按照波形再现振动试验的加载方法和时域疲劳寿命分析方法，研究了峭度和跌宕周期对疲劳寿命的影响，分析了跌宕周期对峭度传递特性的影响规律。

1 非平稳非高斯随机振动的特征和生成

高斯随机振动信号的概率密度函数为

高斯过程可以完全由功率谱密度描述。确定一个随机过程是否为高斯过程的方法是计算该随机过程的高阶矩。随机变量的第阶中心距为

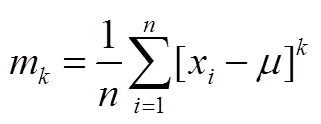
归一化的第3阶中心距称为偏度：

归一化的第4阶中心距称为峭度：

对于高斯过程，偏度=0，峭度=3，偏度不为0或峭度不为3的随机过程即为非高斯过程。峭度表明了时域信号中高峰值出现的概率大小，相比于高斯振动，峭度大于3的非高斯振动表明信号中高峰值出现的概率更大，进而会给产品带来更大的疲劳损伤。非高斯随机信号按其时域特征可以分为2类：一类是均方根值不随时间变化的，称为平稳非高斯振动；另一类均方根值随时间变化的，称为非平稳非高斯振动。飞行器气动噪声、压力振荡、车辆运输时车轴的振动等都属于非平稳非高斯振动[6]。非平稳非高斯信号可以看成是高斯信号被低频正值振荡波形调制的结果。一般地，调制波可以根据式（5）进行提取：

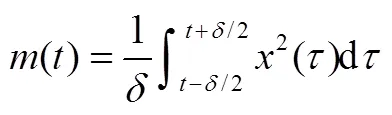
图1为典型的非平稳非高斯信号分解为平稳高斯信号和调制波。

按照规定谱形和峭度生成非平稳非高斯随机振动信号的基础是逆威尔士法，该方法也是生成高斯随机振动信号的常用方法。逆威尔士法的基本原理是，由给定功率谱的幅值与随机相位组合，构造出复数序列。将复数序列进行傅立叶逆变换，形成时域的随机数据块，这个种子数据块与窗函数相乘，延迟叠加后形成平稳的输出，生成非平稳非高斯信号时，将上述的窗函数进行随机化，每一帧种子数据块所加时域窗都经过随机数的标定。按照Smallwood的研究[8]，选择分布作为随机乘数，因为分布极其灵活，而且只产生正值，分布的方差与生成随机数据的峭度之间单调相关，可以用来控制峭度。图2为分布随机数标定窗函数法生成非平稳非高斯信号的过程。

图2 β分布随机数标定窗函数逆威尔士法

2 跌宕周期对非平稳非高斯振动信号的影响

调制波不是严格的周期函数，但是调制波振荡的速率决定了非高斯振动波形的变化速率，调制波振荡的期望周期称为跌宕周期。结合非平稳非高斯信号的生成过程，种子数据块的长度决定了跌宕周期。不同的跌宕周期形成的信号具有相同的概率密度和功率谱，但波形有着明显的差别。图3为跌宕周期对波形的影响，图3a～3d的非高斯波形峭度都等于5，功率谱密度相同。不同跌宕周期信号的概率密度如图4所示，从图4中看到，不同跌宕周期波形的概率密度函数也一致。传统的基于峭度的非高斯疲劳寿命估计方法没有关注到跌宕周期对疲劳寿命的影响，实际上，不同的跌宕周期对结构疲劳损伤有着显著的影响。下文将通过典型结构的计算，讨论非高斯振动的不同参数对疲劳寿命的影响。

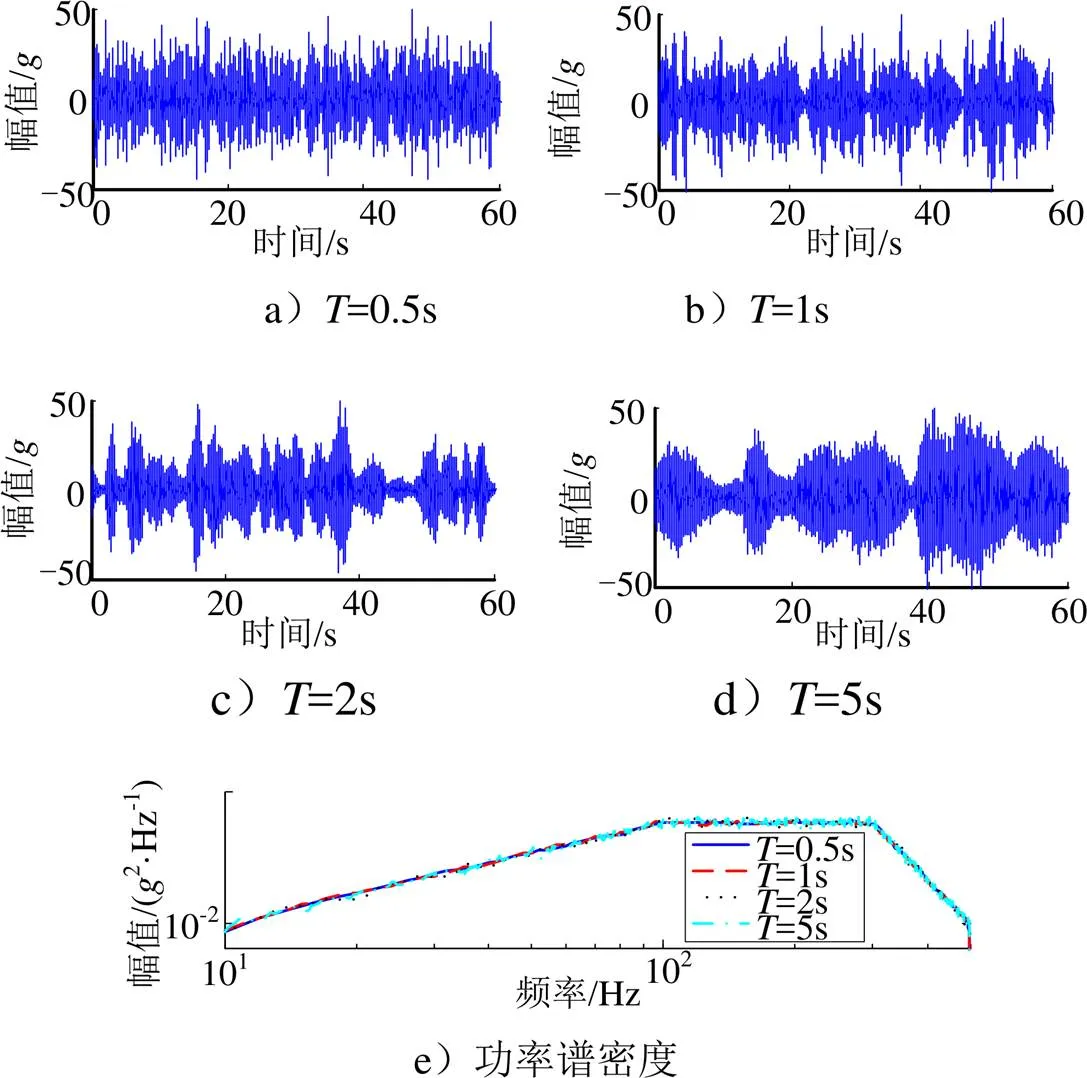
图3 跌宕周期对波形的影响

图4 不同跌宕周期信号的概率密度

3 算 例

通过典型结构的计算，研究非平稳非高斯振动环境中的结构疲劳损伤特性，讨论输入峭度、跌宕周期等参数如何影响疲劳寿命。用来计算的结构是火箭仪器舱里的一个设备支架，在PATRAN中建立了支架的有限元模型，见图5。支架根部连接在舱壁上，支架的负载用集中质量模拟。在仿真计算中，支架的根部固支，施加沿向的加速度基础激励。振动波形的功率谱见图3e。

图5 支架有限元模型

Fig 5 Finite element model of bracket

首先，进行结构的应力脉冲响应计算，获得结构的应力危险点。响应计算使用模态叠加法，设置1%的模态阻尼，在支架根部施加向的单位脉冲激励。图6为应力响应云图，应力最大点位于支架根部连接孔附近，图7为该危险点的应力脉冲响应曲线；然后，计算随机振动基础激励时，危险点的时域应力响应，使用应力危险点的脉冲响应函数，与基础激励时域波形进行卷积计算，得到该点在相应振动下的应力响应；最后，进行疲劳寿命计算。为了完全保留非平稳非高斯振动的时域特征，使用时域疲劳寿命计算方法。选用幂函数形式的S-N曲线，使用雨流循环计数法进行疲劳损伤计算，应用疲劳累积损伤理论估计结构的疲劳寿命。

图6 应力响应云图

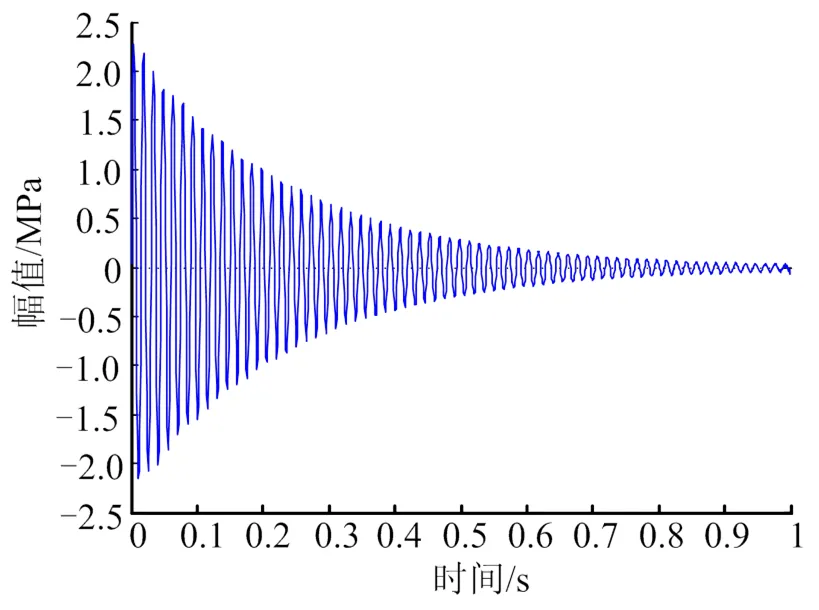
图7 危险点的应力脉冲响应

分别设定非平稳非高斯基础随机振动的峭度为5、7、9，跌宕周期都为0.5 s，计算危险点的疲劳寿命，并同时计算高斯随机振动的结果。考虑到信号的离散性对疲劳寿命计算结果的影响，每个峭度值下计算 50组独立信号的输入，计算结果见图8。由图8可以看出，疲劳寿命和振动峭度有很强的相关性，峭度越高，疲劳寿命越短，=9时的非高斯振动疲劳寿命只有高斯振动时的2.7%。算例显示，随着峭度的增加，结构疲劳寿命趋于稳定，这一特性源于疲劳寿命计算中使用的幂函数形式的S-N曲线。

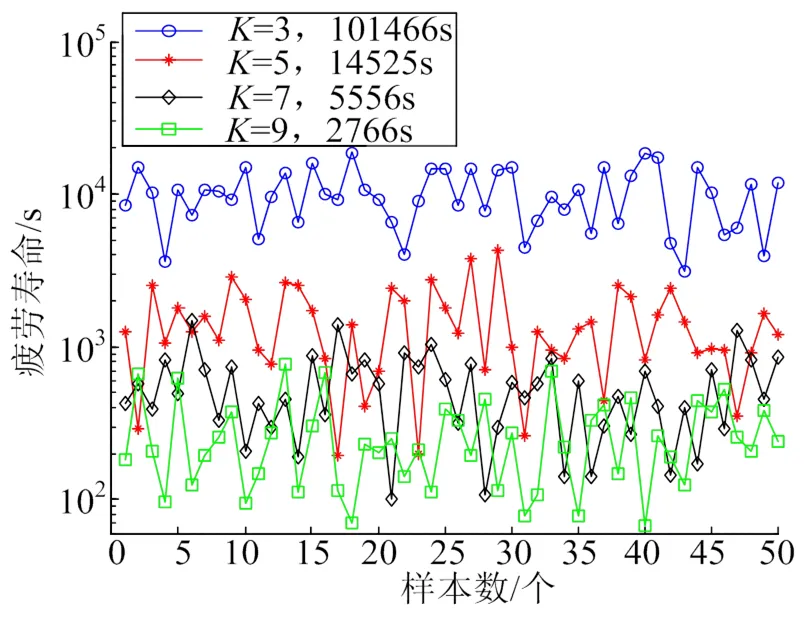
图8 峭度对疲劳寿命的影响

跌宕周期对疲劳寿命有着显著的影响。分别计算峭度为5、7、9时，跌宕周期在0.2～3 s的疲劳寿命随跌宕周期的变化情况，如图9所示。

图9 跌宕周期对疲劳寿命的影响

图9中的计算结果表明，随着跌宕周期的增加，疲劳寿命减小。但疲劳寿命随跌宕周期并非线性变化，超过某一阈值后，疲劳寿命趋向稳定。

对于非高斯振动，危险点的疲劳寿命受制于该点应力响应的峭度，跌宕周期对于疲劳寿命的影响本质上源于跌宕周期对峭度传递的影响。跌宕周期对峭度传递的影响见图10，输出的应力峭度小于输入的振动峭度，随跌宕周期的增加，应力峭度逐渐接近振动峭度，因此疲劳寿命逐渐减小。响应信号峭度的上限是激励信号的峭度，因此增加跌宕周期，结构的疲劳寿命趋于稳定。输出信号是输入信号与结构单位脉冲响应函数的卷积，某一时刻应力响应是很多组非高斯信号的叠加。根据中心极限定理，叠加后的信号逐渐服从高斯分布，因此输出峭度都小于输入峭度。对于跌宕周期更长的信号，幅值中的甚低频分量不易在较短的脉冲响应衰减时间内被平均，因此峭度得以保持[9]。

图10 跌宕周期对峭度传递的影响

Fig 10 Effect on transfer characteristic of kurtosis by roll period

4 结 论

本文开展了非平稳非高斯信号特征分析，以典型航天结构为例，研究峭度和跌宕周期对疲劳寿命的影响，分析跌宕周期对峭度传递特性的影响规律，得到如下结论：

a）峭度和跌宕周期是非平稳非高斯随机振动的表征参数，对结构疲劳寿命有显著的影响。振动峭度越高，疲劳寿命越短，高峭度非高斯振动下的疲劳寿命比高斯振动的小1～2个数量级。随着跌宕周期的增加，疲劳寿命减小。跌宕周期对疲劳寿命的影响源于跌宕周期对峭度传递的影响。峭度和跌宕周期对结构疲劳寿命的影响随着量值的增加而趋于稳定。

b）跌宕周期反映了信号时域特征。进行非高斯振动试验设计时，对实测振动环境进行跌宕周期的提取和统计，在传统峭度控制基础上加入跌宕周期再现，将有效提高环境模拟真实性，提高疲劳寿命估计精度。

[1] 袁毅, 程军圣. 一种新的非高斯随机振动疲劳寿命估计方法[J]. 振动与冲击, 2014, 33(18): 209-213.

YUAN Yi, CHENG Junsheng. A new method for fatigue life estimation under non-Gaussian random vibration[J]. Journal of Vibration and Shock, 2014, 33(18): 209-213.

[2] 吴家驹, 张鹏飞, 胡亚冰. 非高斯随机振动的分析基础[J]. 强度与环境, 2018, 45(2): 1-8.

WU Jiaju, ZHANG Pengfei, HU Yabing. Analytical basis for the synthesis of non-Gaussian random vibration[J]. Structure & Environment Engineering, 2018, 45(2): 1-8.

[3] 徐飞, 李传日, 姜同敏, 等. 非高斯随机振动的模拟方法[J]. 北京航空航天大学学报, 2014, 40(9): 1239-1244.

XU Fei, LI Chuanri, JIANG Tongmin, et al. Simulation of non-Gaussian random vibration[J]. Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(9): 1239-1244.

[4] 蒋瑜, 陶俊勇, 陈循. 超高斯随机振动疲劳加速试验模型[J]. 振动与冲击, 2017, 36(9): 261-266.

JIANG Yu, TAO Junyong, CHEN Xun. Super-Gaussian random vibration fatigue accelerated testing model[J]. Journal of Vibration and Shock, 2017, 36(9): 261-266.

[5] JOHN V B, PHILIP V B. The third dimension of random vibration control[C]. Annapolis: 24th Space Simulation Conference, 2006.

[6] FREDERIC Kihm, STEPHEN A R, NEIL S F, et al. Understanding how kurtosis is transferred from input acceleration to stress response and its influence on fatigue life[R]. NASA NF1676L-15395, 2014.

[7] 吴家驹, 付玮, 张鹏飞. 基于分布随机数排序的非高斯振动模拟方法[J]. 强度与环境, 2017, 44(2): 10-17.

WU Jiaju, FU Wei, ZHANG Pengfei. Simulation method of non-Gaussian vibration base on re-arrangement ofdistribution random number[J]. Structure & Environment Engineering, 2017, 44(2): 10-17.

[8] David O S. Vibration with non-Gaussian noise[J]. Journal of the IEST, 2009, 52(2): 13-30.

[9] FREDERC Kihm, NEIL S, JEROME Antoni. Fatigue life from kurtosis controlled excitations[J]. Procedia Engineering, 2015(133): 698-713.

Fatigue Life Analysis of Aerospace Structures based on Non-stationary Non-Gaussian Random Vibration

ZHANG Pengfei, DING Zhenjun, CHEN Guiling, WU Jiaju

(Beijing Institute of Structure and Environment Engineering, Beijing, 100076)

Random vibration test is a usual method for structure fatigue life assessment. Vibration signal is assumed to fit the normal distribution usually. Non-stationary non-Gaussian vibration environment exists in actual use environment. Fatigue life analysis of structure in non-stationary non-Gaussian environment is conducive to improving test technique. Feature and generating method of non-stationary non-Gaussian random vibration is introduced. Effect on time domain wave shape by roll period is analysed. A typical finite element model is built, and effect of kurtosis and roll period on fatigue life is researched, according to waveform reproduction test method and time domain fatigue life analysis technique. The results show that kurtosis and roll period has significant effects on fatigue life. The research is of useful for reference to increasing authenticity of environment test, and improving technology of fatigue life test.

non-stationary; non-Gaussian; fatigue life; roll period

2097-1974(2023)02-0109-05

10.7654/j.issn.2097-1974.20230221

V414

A

2020-05-01；

2020-07-31

张鹏飞（1986-），男，高级工程师，主要研究方向为结构动力学。

丁镇军（1984-），男，高级工程师，主要研究方向为多维振动试验技术。

陈贵龄（1987-），男，工程师，主要研究方向为环境工程。

吴家驹（1939-），男，研究员，主要研究方向为非平稳非高斯动力学试验技术研究。