火箭飞行跨声速激波现象研究
张耘隆,何 巍,高武焕,黑艳颖,刘汉宇
火箭飞行跨声速激波现象研究
张耘隆,何 巍,高武焕,黑艳颖,刘汉宇
(北京宇航系统工程研究所,北京,100076)
在运载火箭飞行过程中,由于火箭气动外形的变化,在跨声速飞行段运载火箭整流罩柱段外部会产生跨声速激波现象。为了研究火箭整流罩外部流场中跨声速激波的变化规律,采用三维数值模拟,获取了运载火箭跨声速飞行外部流场,并采用试验结果验证了数值方法的正确性。使用数值纹影对跨声速激波进行了显示,获取了激波位置随着飞行马赫数的变化规律,研究了激波前后压差随着飞行马赫数的变化规律。
运载火箭;跨声速激波;压差
0 引 言
运载火箭在飞行过程中速度从0一直加速到几千米每秒,飞行的速度区域从亚声速、跨声速、超声速一直到高超声速,其中流动现象最为复杂的是跨声速飞行过程[1-3]。在跨声速飞行过程中,火箭会承受严酷的跨声脉动压力环境和内外压差载荷。因此开展运载火箭飞行跨声速流场研究具有重要的意义。
在运载火箭跨声速飞行段,流场结构会发生快速变化。气流在火箭整流罩锥柱交界面后的区域加速,当飞行速度增加到一定程度,在锥柱交界面后区域首先达到声速,同时在运载火箭表面会出现跨声速激波现象。跨声速激波会快速移动经过运载火箭的外表面,给运载火箭整流罩外表面带来剧烈的压力变化。整流罩外表面压力的迅速变化会带来内外压差载荷的变化。
Charles[4]通过风洞试验研究了不同整流罩外形下的箭体表面脉动压力特性;Deese等[5]开展了运载火箭分离流动预示研究,研究中主要对比了湍流模型对倒锥处分离流动的预示能力,仿真预示有效捕捉到了整流罩柱段的跨声速激波;Rajan等[6]在风洞试验中系统研究了整流罩直径比和倒锥角对整流罩倒锥处跨声速脉动压力分布的影响,当倒锥角达到一定值时,倒锥后脉动压力不再变化;Rakhab等[7]针对锤头型运载火箭整流罩开展了数值模拟研究,仿真给出了整流罩倒锥分离流动所导致的表面脉动压力声压级和频谱特性;David等[8]通过飞行、风洞和数值方法研究了细长双锥构型在马赫数为0.6、1.5和1.8下的表面平均静态压力分布和脉动压力特性;Mehta[9]通过数值仿真获取运载火箭表面在跨声速的压力分布,研究了火箭整流罩内外压差特性,但是未对整流罩跨声速激波的规律开展研究。后续的研究工作大都针对运载火箭整流罩跨声速脉动压力问题[10-13],对运载火箭跨声速飞行激波问题尚缺乏研究。本文对运载火箭跨声速飞行中激波现象开展研究,从而更好地认识运载火箭跨声速流动及整流罩内外压差载荷。
1 数值仿真模型
1.1 网格策略
为了有效捕捉流场结构,针对运载火箭构型开展了分区域多层O型网格策略,网格数量约为900万,网格拓扑结构如图1所示。
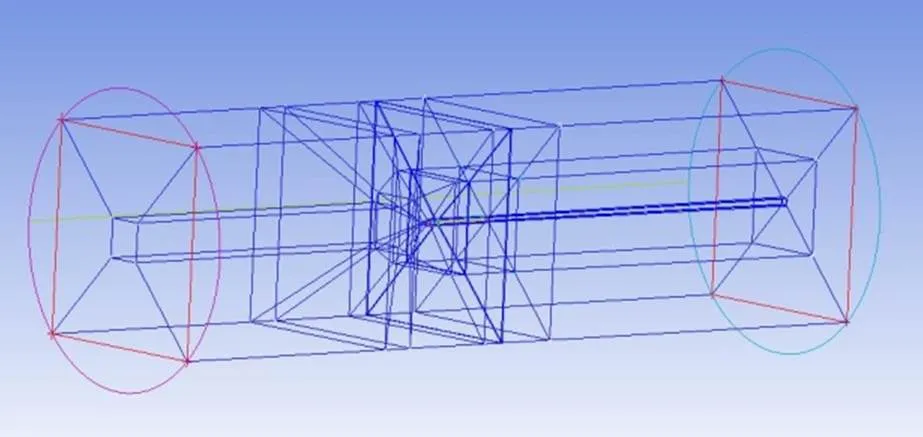
图1 网格拓扑结构
1.2 数值方法
1.2.1 控制方程
直角坐标系下的N-S方程为
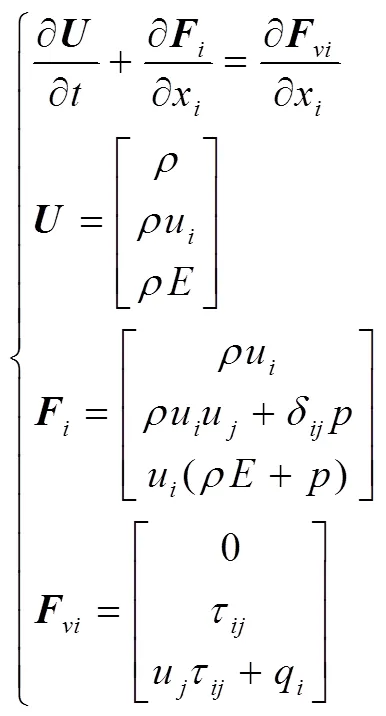
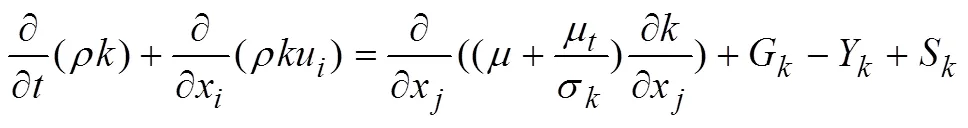
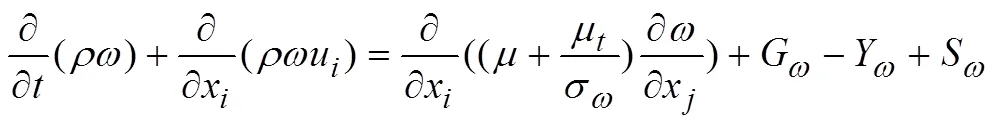
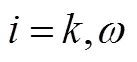
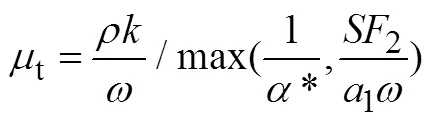
结合流场N-S方程、理想气体状态方程和湍流输运方程,可以求解出所有流场参数。
1.2.2 边界条件
采用无滑移绝热壁面条件,即:
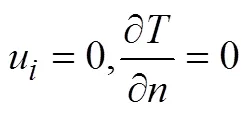
外部远场给定来流速度、温度和压力条件,出口边界则根据给定压力出口条件。
1.2.3 数值方法
本文采用有限体积法求解上述方程组。通量分裂采用Roe格式,对流项采用二阶精度迎风格式离散。
2 仿真结果分析
2.1 仿真计算工况
针对单芯级构型开展仿真计算分析,火箭的整流罩为冯·卡门曲线,具体的构型情况见图2。轴沿箭体的轴线方向,从箭体头部指向尾部,轴方向为图2中竖直向上方向,轴方向与、轴方向构成右手坐标系。为了研究运载火箭流场中的跨声速激波现象,开展了如表1所示工况的计算,来流马赫数在0.7~0.95之间,气流攻角为0°,同时列出了弹道高度随马赫数的变化。

图2 仿真计算的火箭构型
表1 计算工况
Tab.1 Simulation conditions
马赫数高度/km马赫数高度/km 0.705.140.856.56 0.725.360.866.69 0.745.570.886.82 0.765.710.907.08 0.785.840.927.33 0.806.060.947.48 0.826.310.957.60 0.846.43——
2.2 仿真结果验证
图3为整流罩肩部附近的无量纲外压变化情况。由图3可知,试验测量显示,整流罩外压随飞行时间下降,某一时刻突然下降。根据弹道马赫数和大气模型,可以将模拟得到的压力系数换算为真实压力。仿真的计算压力和试验结果变化规律一致,存在迅速下降的现象,出现突跳下降的马赫数也和试验结果接近,证明本文采用的数值仿真方法能够较好地捕捉到跨声速激波现象。

图3 整流罩肩部压力变化
2.3 仿真结果分析
外部高速气流经过火箭外表面,由于运载火箭头部外形的变化,气流在运载火箭整流罩锥段和柱段的交界面附近加速。气流首先在运载火箭整流罩锥段和柱段的交接面附近达到超声速,超声速气流以一道激波结束。图4给出了马赫数分别为0.70、0.76、0.80、0.85、0.90、0.95的6个工况的马赫数云图和压力云图。图中结果表明:a)随着来流马赫数的逐渐增大,整流罩锥段和柱段交接面后的超声速区不断增大;b)超声速区结束激波的位置在不断向箭体尾部移动。根据可压缩流动的规律,气流流动速度增加,气流压力下降,因此超声速区对应为流场中的低压区,图4中的压力分布云图与分析一致。

图4 部分工况流场云图
为了更加清晰地观察激波的位置,采用数值纹影对流场进行了显示。数值纹影的定义采用Hadjadj等[14]在高速气体动力学流场显示研究中的方法,其定义形式如式(6)所示:

采用上述计算方法获取的流场数值纹影如图5所示,马赫数包括0.70、0.76、0.80、0.85、0.90和0.95。从图5中可以看到,在整流罩锥段和柱段交接面后面存在高亮条带,该条带即是上文中提到的激波。对比6个马赫数下的数值纹影,可以发现:a)在马赫数为0.7和0.76时激波尚不明显,在马赫数为0.8时出现了明显的激波;b)激波位置随着马赫数增加逐渐向箭体尾部方向移动,同时激波的长度不断增大。

图5 部分工况流场数值纹影云图
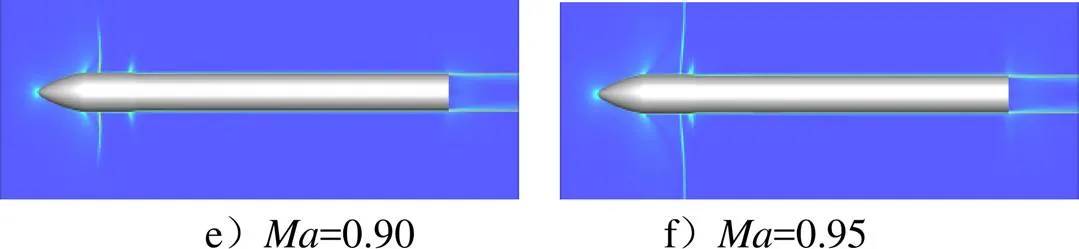
续图5
2.4 跨声速激波分析
气流经过激波后,压力迅速上升,同时伴随着速度迅速降低,温度迅速升高。跨声速激波最终会作用到箭体外表面上,影响火箭外表面的压力分布。为了深入研究火箭跨声速激波对箭体壁面的压力影响,将仿真计算的各个工况的箭体母线上的压力提取出来。火箭飞行过程中箭体母线上的压力沿箭体轴线的分布如图6所示,箭体锥柱交界面后的压力迅速下降,然后箭体外表面产生一道激波,经过激波时箭体外表面压力迅速上升。运载火箭跨声速飞行时,由于箭体整流罩内部压力在同一个时刻基本为同一个值,箭体外表面压力的迅速下降将给整流罩局部外表面带来较大的内外压差载荷。

图6 整流罩局部母线压力分布
激波前后压差定义见图7。
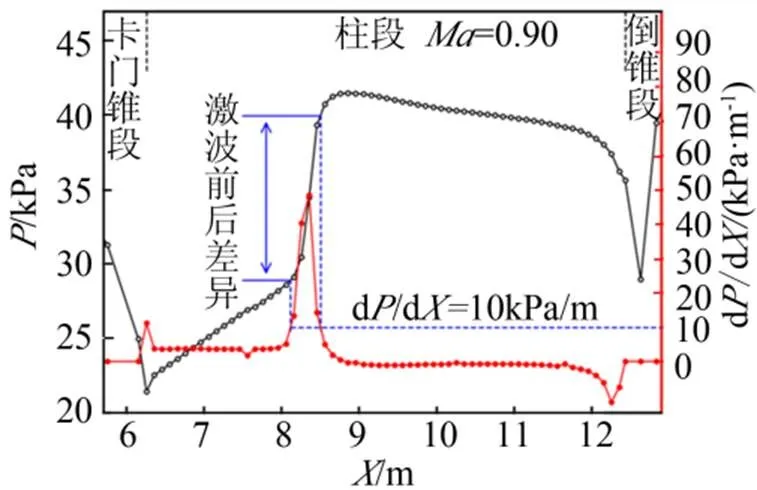
图7 激波前后压差定义
激波从物理上是流场中的强间断,激波厚度实际为0.1 m。在数值计算中由于存在数值粘性耗散,激波在数值计算中会变厚,但是数值仿真依然能够捕捉到流场的剧烈压力变化。为了进一步表征跨声速激波前后箭体表面压力变化情况,针对整流罩母线上的压力分布对箭体轴向坐标求导,定义d/d为10 kPa/m的起始位置和终止位置的箭体表面压力差为跨声速激波前后压差,同时定义dd最大的位置为激波位置。
图8给出了跨声速激波前后箭体表面的压力变化和激波位置随着飞行马赫数的变化情况。激波前后的压差与激波的强弱有关,激波前后压差越大,激波强度越强。由图8可知,仿真计算的激波前后压差随着马赫数增大先增大后降低,即激波强度先增强后减弱。激波前后箭体表面压差最大值出现在马赫数0.78左右,激波前后壁面最大压差为15.2 kPa。此外,激波位置随着马赫数增加不断向箭体尾部方向移动,激波位置随着马赫数非线性变化,激波位置随马赫数变化的斜率不断增大。
为了更好地获取运载火箭外表面压力分布,在火箭风洞试验工况设计上,应减小马赫数0.8到1.0之间的马赫数间隔,从而能够有效捕捉到火箭整流罩外表面的跨声速激波移动现象,为运载火箭排气孔设计提供更加详细的压力分布数据。
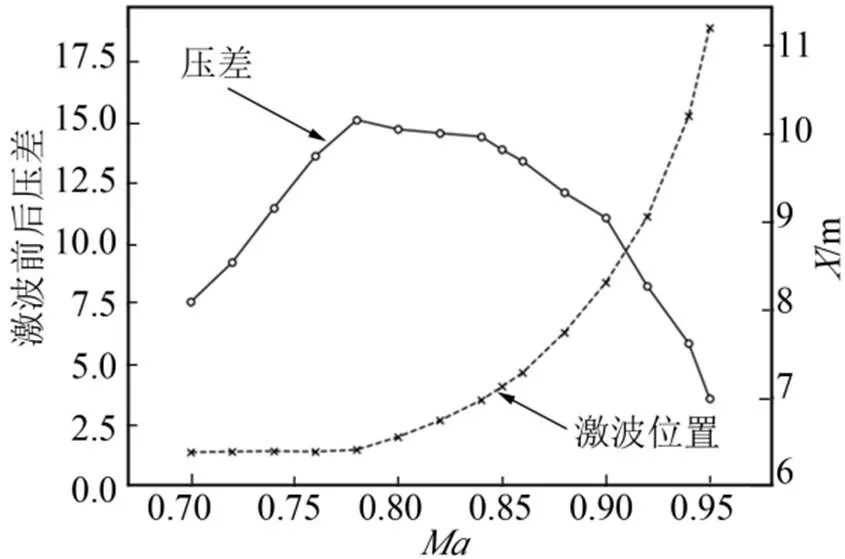
图8 火箭跨声速飞行激波前后压差和激波位置随着马赫数的变化情况
3 结 论
本文采用数值模拟对一种冯·卡门曲线整流罩单芯级运载火箭跨声速飞行流场进行了仿真计算,采用数值纹影对跨声速激波现象开展了研究分析。经过分析得出如下结论:a)在运载火箭跨声速飞行过程中,跨声速激波位置随着马赫数增大向箭体尾段移动,激波位置随马赫数非线性移动,激波位置变化斜率逐渐增大;b)跨声速激波前后的压差随着马赫数先增大后减小,激波强度先增强后减弱;c)激波前后最大压差约为15.2 kPa出现在=0.78附近;d)从运载火箭内外压差载荷设计角度,应当在马赫数0.8~1.0区间加密风洞试验工况。
[1] 牟宇, 樊晨霄, 何兆伟. 运载火箭创新技术驱动构型优化规律研究[J]. 导弹与航天运载技术(中英文), 2022(6): 57-63.
MOU Yu, FAN Chenxiao, HE Zhaowei. Research on optimization law of launch vehicle innovative technology driving configuration[J]. Missles and Space Vehicles, 2022(6): 57-63.
[2] 沈丹, 彭博, 李舟阳, 等. 火箭协同优化中的气动代理模型研究[J]. 宇航总体技术, 2020(5): 44-50.
SHEN Dan, PENG Bo, LI Zhouyang, et al. Research on aerodynamic surrogate madeling for launch vehicle collaborative optimization[J]. Astronautical Systems Engineering Technology, 2020(5): 44-50.
[3] 梁明. 某型飞行器气动参数辨识与弹道仿真[J]. 上海航天(中英文), 2022, 39(5): 140-146.
LIANG Ming. Aerodynamic parameter identification and ballistic simulation of a certain aircraft[J]. Aerospace Shanghai(Chinese & English) , 2022, 39(5): 140-146.
[4] CHARLES F C. The effects of some variations in launch-vehicle nose shape on steady and fluctuating pressures[R]. NASA TM X-646, 1962.
[5] DEESE J E, GIELDA T P, AGARWAL R K. Prediction of flow separation on launch vehicle configurations[R]. AIAA-1991-1727, 1991.
[6] RAJAN Kumar, VISWANATH P R. Mean and fluctuating pressure field in boat-tail separted flows at transonic speeds[R]. AIAA-2001-0528, 2001.
[7] RAKHAB C M. Investigation of unsteady behavior of separated flow in the boattail region of bulbous payload shroud[R]. AIAA-1998-2408, 1998.
[8] DAVID J P, DAVID F F, DAVID S M. Flight, wind tunnel, and numerical experiments with a slender cone at incidence[J]. AIAA Journal, 1981(20): 1338-1345.
[9] MEHTA R C. Estimation and comparison of discharge coefficient for satellite launch vehicles payload fairing vents[R]. AIAA-2002-3152, 2002.
[10] Seiji Tsutsumi, Ryoji Takaki. Hybrid LES/RANS simulations of transonic flowfield around a rocket fairing[R]. AIAA-2012-2900, 2012.
[11] 赵瑞, 荣吉利, 李跃军, 等. 整流罩母线形状对脉动压力环境的影响研究[J]. 兵工学报, 2017, 38(5): 1020-1026.
ZHAO Rui, RONG Jili, LI Yuejun, et al. An investigation of fluctuating pressure environment around rocket fairing with different curvetypes[J]. Acta Armamentarii, 2017, 38(5): 1020-1026.
[12] LIU Yi, WANG Gang, ZHU Hongyu, et al. Numerical analysis of transonic buffet flow around a hammerhead payload fairing[J]. Aerospace Science and Technology, 2019(84): 604-619.
[13] WANG Gang, LI Quanzheng, LIU Yi. IDDES method based on differential Reynolds-stress model and its application in bluff body turbulent flows[J]. Aerospace Science and Technology, 2021(12): 119-132.
[14] HADJADJ A, Kudryavtsev A. Computation and flow visualization in high-speed aerodynamics[J]. Journal of Turbulence, 2005(6): 1-25.
The Study of Transonic Shock Wave during Launch Vehicle Flight
ZHANG Yunlong, HE Wei, GAO Wuhuan, HEI Yanying, LIU Hanyu
(Beijing Institute of Astronautical Systems Engineering, Beijing, 100076)
Because of the variation of the launch vehicle profile, a transonic shock wave exists on the cylinder part of the fairing during the transonic flight. For the studying of variation of the transonic shock wave in the flow field around the rocket fairing, the flow field is obtained using a three-dimensional simulation and the method is validated by test data. The transonic shock wave is visualized by the numerical schlieren method, and the variation of the shock wave position with the Mach number of the far field flow is analyzed. The pressure difference across the shock wave characteristic with the far field Mach number is studied.
launch vehicle; transonic shock wave; pressure difference
2097-1974(2023)02-0001-05
10.7654/j.issn.2097-1974.20230201
V475.1
A
2022-11-29;
2023-02-16
张耘隆(1986-),男,高级工程师,主要研究方向为运载火箭总体设计。
何 巍(1978-),男,研究员,主要研究方向为运载火箭总体设计。
高武焕(1991-),男,工程师,主要研究方向为运载火箭气动力和气动热设计。
黑艳颖(1987-),女,工程师,主要研究方向为运载火箭总体设计。
刘汉宇(1995-),男,助理工程师,主要研究方向为运载火箭气动力和气动热设计研究。

