半柔壁喷管初步实验研究

彭 强，廖达雄，秦红岗，易星佑

（中国空气动力研究与发展中心空气动力学国家重点实验室，四川绵阳 621000）

0 引 言

跨超声速试验能力是衡量一个国家军事航空能力的一个重要方面。超声速风洞作为超声速试验的重要地面气动设备，在军用飞机、导弹和航天气动试验中起着不可替代的作用。超声速喷管是超声速风洞建立超声速流场的核心部段，其设计质量的高低，直接决定了超声速风洞的流场品质，决定了超声速风洞试验数据的可靠性和精度，决定了超声速风洞的试验能力以及风洞的运行效率。现阶段，西方发达国家先进的大尺寸跨、超声速生产性风洞一般均配置半柔壁喷管，以实现变马赫数的目的，但国内至今还没有掌握该项设计技术。

半柔壁喷管型式与国内已使用的全柔壁喷管型式相比，存在以下特点：半柔壁喷管中，喉道部分为固块，膨胀区使用柔壁，由于在弯曲率最大的喉道部分使用了固块（见图1），因此喷管柔板长度可减少近一半，可以降低对柔板材料和柔板加工的苛刻要求，喷管建造经费可减少20%～30%；柔壁驱动支撑点数量大大减少，控制程序简洁，喷管型面曲线可由少数支撑杆控制形成，机构整体刚性好，喷管型面在承压状态下，可有效抑制喷管型面失稳现象。因此，可在风风洞运行过程中实现连续变马赫数，风洞运行效率大大提高。

图1 半柔壁喷管示意图Fig.1 Diagram of semi－flexible nozzle

目前，国内超声速风洞的喷管主要使用固块模式，小部分超声速风洞使用全柔壁模式，如气动中心的0.3m跨超声速风洞、1.2m跨超声速风洞。但国内还没有半柔壁喷管用于大型生产性跨、超声速风洞中。为解决该工程设计技术问题，需在3个方面开展工作：一是喷管型面设计方法、二是流场数值模拟及设计参数优化、三是试验研究。对于第一、二方面的工作，在前期已经完成［1－9］，该研究的主要内容，是以0.3m跨超声速风洞为研究平台，通过试验研究手段，测试半柔壁喷管流场，验证半柔壁喷管设计方法的可靠性和有效性，为下一步高品质流场半柔壁喷管的设计打下基础。半柔壁喷管试验件的设计指标为：（a）试验段马赫数变化范围0.5～3.0；（b）试验段马赫数控制精度，｜d M／M｜≤1%；（c）在风洞吹风过程中，可实现马赫数的连续变化。

1 试验设备介绍

半柔壁喷管进行试验的平台是0.3m跨超声速风洞［2］，为下吹型式（见图2），试验段尺寸为：0.3m× 0.3m×0.9m（宽×高×长），马赫数范围为0.3～3.5，试验段雷诺数范围为0.65×107～6.8×107（1／m），该风洞主要用于开展风洞部件性能研究。风洞由以下部段组成：截止阀、调压阀、进气管道、大扩开角段、稳定段、圆方过渡段、喷管段、试验段、超声速扩散段、方圆过渡段、亚声速扩散段、排气段、排气消声器。气动布局见图2。0.3m跨超声速风洞配置有全柔壁喷管，半柔壁喷管试验件就安装在原全柔壁喷管所在位置。在试验段出口处配置了模型支架，以及试验段测压排架的移测机构，可使用单点探针和25点“十字型”总压排架对试验段流场进行测量。风洞配置了纹影系统，可用于试验段的流场观察，纹影系统口径220mm，观察中心位于距试验段入口550mm处。

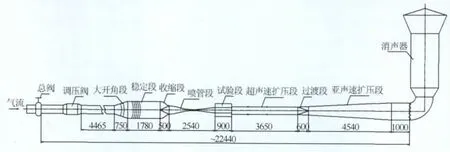
图2 0.3m跨超声速风洞示意图Fig.2 Outline of 0.3mtran－supersonic wind tunnel

用于试验的半柔壁喷管段见图3、4。在结构上，0.3m跨超声速风洞半柔壁喷管系统包括收缩段和与之相连的半柔壁喷管，收缩段入口与现有稳定段相接，半柔壁喷管出口与现有试验段相接。半柔壁喷管主要由基座、下梁、上梁、左右侧壁和半柔壁组件组成，采用法兰面连接的方式与前端收缩段和后端试验段连接。半柔壁喷管上下由6对电动推杆支撑，通过推杆的协调动作，控制喷管壁板形成所需要的喷管气动型面，实现连续变马赫数的目的。

图3 半柔壁喷管气动轮廓图Fig.3 Outline of semi－flexible nozzle

图4 半柔壁喷管实景图Fig.4 Picture of semi－flexible nozzle

2 试验结果及分析

针对半柔壁喷管的试验研究，主要介绍了半柔壁喷管动调的过程和结果，以及喷管流场的最终测试结果。由于篇幅限制，只针对马赫数为1.5的典型状态进行试验结果分析。

2.1 半柔壁喷管动调

喷管完成在风洞上的安装和静调后，需要进行动调，其目的有两个。一是检验各运动部件在风洞运行状态下的性能是否满足要求，二是通过动调，使用影响法优化各马赫数下的撑杆位置，提高试验段马赫数均匀性。通常采用试验影响法进行柔壁喷管型面调试，其基本原理是：当流场的变化量是撑杆位移的线性函数时，则微调撑杆对流场的影响满足迭加原理。这样通过试验建立每一根撑杆位移变化与所引起的喷管试验区气流变化关系（即所谓的试验影响曲线），并利用这些试验影响曲线求解积分方程。理论上，在流场中加入一个任意分布函数C（x），可以获得完全均匀的流场，但实际能做到的最佳修正也只能逼近C（x）。利用最小二乘法概念，最佳的修正是使得喷管试验段中某区域的实际修正量和理想修正量之间的差值达到最小值，该条件表示为：

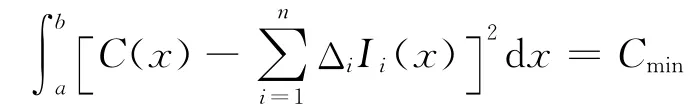
式中：Δi——第i根撑杆的位移；

Ii（x）——第i根撑杆的影响曲线。

Cmin必须对于n根投入修正的任意一根都适用，则：

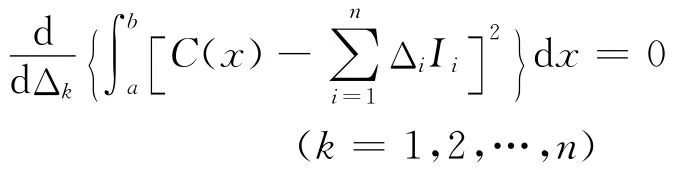
进行运算后，上式简化为以撑杆调节量表示的n线线性联立方程组：

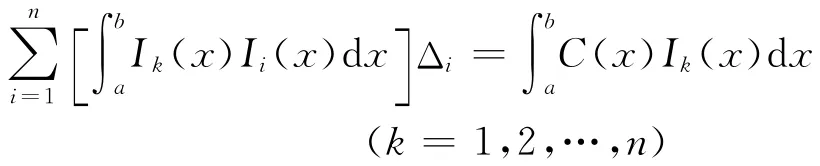
就可得到最佳流场的各撑杆的实际调节量Δi，其中C（x）是在试验区产生完全均匀流场的理想修正量，Ii（x）是测量得到的第i根撑杆的单位位移对x点气流的马赫数的影响量。

通过使用试验影响法对喷管进行动调后，试验段流场将会得到有效改善。

在半柔壁喷管上下柔壁支撑点附近，各设置了4个应力监测点，在风洞吹风过程中，监测柔板应力变化，并与风洞控制系统安全连锁，在出现应力值超过允许范围时，风洞自动停车。在半柔壁喷管进行动调前，已经完成了静调测试，通过静调和动调的应力比较，应力最大相差在20MPa以内，可以认为柔板在型面成型后，风洞吹风和不吹风，喷管柔板应力相差不大。

动调过程：一是测试出原始型面的试验段轴线上马赫数分布，作为动调的初始状态；二是测试出每对上下撑杆同步相同移动微量距离后，测量出试验段相同区域轴线上的马赫数变化曲线，通过影响法数据处理方法，计算出各对撑杆需要修正的位移量，并对型面进行修正；三是对修正后的型面进行马赫数分布测试，如有必要，进行第二次修正。

半柔壁喷管上下总共设置6对电动撑杆，顺气流方向编号为1～6号，1、2号撑杆用于驱动喉道固块，3～6号撑杆用于驱动柔板，因此对半柔壁喷管的动调主要是针对3～6号撑杆。利用纹影照相，结合在流场观察区建立的坐标系，通过使用定位软件，可以确定出流场中主要波系的反射位置，从而粗略判断出激波在壁面上产生的位置。

图5～7为M＝1.5的动调结果，从纹影处理的图像，可以判断出在喷管与试验段结合区域，产生了一道较强的斜激波，第一菱形区的顶点位置基本位于喷管出口。在每对撑杆单独往远离喷管轴线方向移动1mm，测出每对撑杆对试验段的影响曲线，经过计算，得到每对撑杆的修正量，对喷管型面进行调整，对新的型面流场进行测试。从校测后的马赫数分布可以看出，喷管静调中出现的一些马赫数波动被削弱，流场均匀性有较大的提高，一次动调的预测马赫数分布，与实际测量的马赫数分布有较好的一致性。

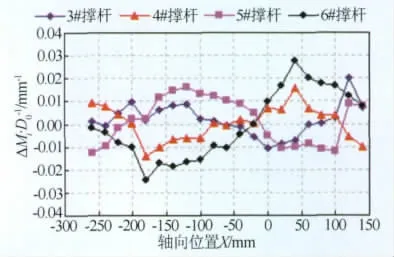
图5 半柔壁喷管动调影响曲线（M＝1.5）Fig.5 Testing influence curve of semi－flexible nozzle（M＝1.5）

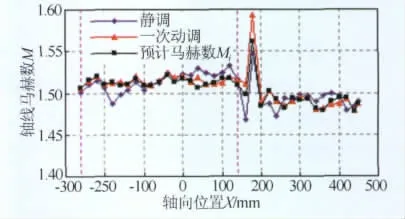
图6 半柔壁喷管动调结果（M＝1.5）Fig.6 Dynamic debugging results of semi－flexible nozzle（M＝1.5）

综合其它各典型马赫数下的动调数据，动调后比静调的马赫数均匀性有较大提高，但第一次动调和第二次动调，流场改善不大。表1为各马赫数下型面动调后，试验段第一菱形区轴线上马赫数均方根偏差。马赫数均方根偏差的预测值与实测值相比，均偏于乐观，第二次动调的结果可能会更差。

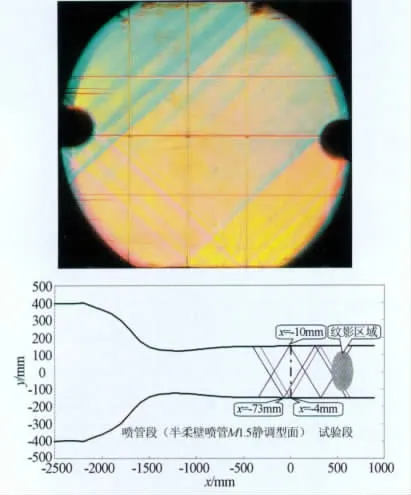
图7 激波反推位置示意图（M＝1.5）Fig.7 Schematic of shock wave in the test section（M＝1.5）

表1 第一菱形区轴线马赫数分布均方根偏差动调结果Table 1 The distribution of mean square root of M along the first rhombus region axis

在M＝1.5时，一次动调后试验段第一菱形区轴线马赫数均方根偏差达到0.0055，优于0.006的国军标先进指标。对M＝2.0、2.5、3.0的马赫数均方根偏差分别为0.0098、0.0105、0.0098，接近各马赫数下的先进指标0.007、0.008、0.009。各马赫数经动调后，均方根偏差一般减少30%～40%，动调效果非常明显。

2.2 半柔壁喷管流场测量

在完成半柔壁喷管的动调后，对主要马赫数下的流场进行了校测，不仅测试各马赫数下沿试验段轴线的马赫数分布，还测试沿试验段轴线的水平和竖直截面马赫数分布，以判断试验段马赫数分布均匀性的整体情况。图8～10为M＝1.5的流场马赫数分布测试结果，在轴向马赫数分布曲线上，距试验段入口0.51m处存在一个马赫数的峰值，从马赫数云图上看（水平截面，左／上为正），存在两道斜激波相交，分析其原因是由喷管段与试验段连接处产生的激波造成的（见图10）。其余区域的马赫数分布较均匀。沿试验段轴线，水平截面上马赫数均方根偏差范围为0.004～0.04（全柔壁喷管为0.004～0.012），竖直截面上马赫数均方根偏差范围为0.008～0.025（全柔壁喷管为0.004～0.018），与全柔壁喷管对应区域相比，截面均方根偏差要高一些。

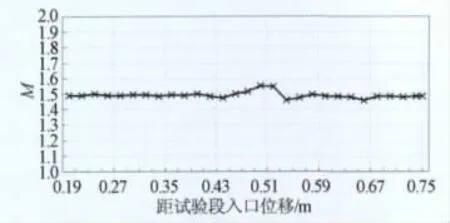
图8 半柔壁喷管试验段轴线马赫数分布（M＝1.5）Fig.8 Distribution of axial Mach number in test section（M＝1.5）

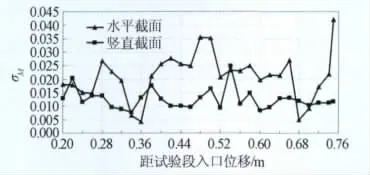
图9 半柔壁喷管沿试验段轴线截面马赫数均方根偏差（M＝1.5）Fig.9 Distribution of axialσMin test section（M＝1.5）

图10 半柔壁喷管试验段过轴线水平截面马赫数云图（M＝1.5）Fig.10 Contour of Mach number in horizontal cross section of test section（M＝1.5）

图11～12为M＝3.0的流场马赫数分布测试结果，在距试验段入口0.29～0.53m范围内，马赫数波动较大。沿试验段轴线，水平截面上马赫数均方根偏差范围为0.008～0.035（全柔壁为0.01～0.048），竖直截面上马赫数均方根偏差范围为0.012～0.063（全柔壁为0.01～0.05），与全柔壁对应区域相比截面均方根偏差相当。

从上面分析综合来看，半柔壁喷管与全柔壁喷管相比，在试验段的第二菱形区内，截面马赫数均方根偏差指标要差一些，这为半柔壁喷管的下一步改进指出了方向。

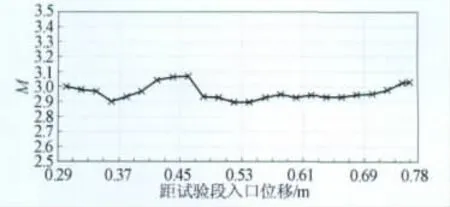
图11 半柔壁喷管试验段轴线马赫数分布（M＝3.0）Fig.11 Distribution of axial Mach number of test section（M＝3.0）

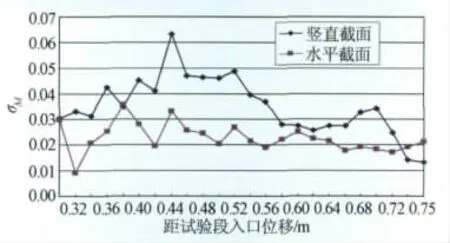
图12 半柔壁喷管沿轴线截面马赫数均方根偏差（M＝3.0）Fig.12 Distribution of axialσMof test section（M＝3.0）

2.3 半柔壁喷管变马赫数试验

在风洞吹风过程中进行马赫数变化，是半柔壁喷管相对全柔壁喷管的优势之一。为此，在喷管进行变马赫数过程中，测试了距试验段入口0.4m截面上马赫数的均匀性变化。

在进行变马赫数试验时，有几点情况需要说明：

（a）在喷管马赫数变化时，各撑杆按怎样的规律运动，才能保证流场马赫数的均匀性。例如从马赫数1.5变化到2.0，采取的策略是：首先校准出马赫数1.6、1.7、1.8、1.9的喷管型面，各撑杆按等比例运动规律，控制型面从马赫数1.5变化到1.6，从1.6变化到1.7，以此类推，直到马赫数2.0，由此可尽可能地保证喷管型面是气动型面。

（b）电动推杆的运动不是匀速运动，每个撑杆从一个位置到另一个位置，有一个加速匀速减速的过程，如从马赫数1.5到1.6，均有这个过程。因此，在设定的从马赫数1.5变化到2.0时，整个过程不是匀速变化的，是一个不断变速的过程。

（c）半柔壁喷管撑杆的最高移动速度设定为1mm／s。

（d）测量采样频率为20Hz。

（e）试验段中安装25点的十字排架，用于测量流场均匀性。

图13为喷管马赫数从1.5变化到2.0时，距试验段入口0.4m试验段中心点的马赫数随时间变化曲线，由于电动推杆的不连续运动，马赫数随时间的变化不是一条单调的光滑曲线。图14为距试验段入口0.4m水平方向的马赫数分布均方根偏差，在开始和结束的一段平直曲线的值，分别代表了马赫数1.5和2.0的马赫数均方根偏差。在马赫数变化过程中，有部分曲线值低于开始和结束时的均方根偏差，这说明，在喷管进行变马赫数过程中，试验段的马赫数均匀性，有好于固定喷管型面时的状态，这与我们的预期不一致。其原因可能是在马赫数在1.5至2.0之间的某些型面下，喷管流场均匀性比马赫数1.5和 2.0的要好，这只需要在下一阶段流场测试中，挑选一定的马赫数型面进行流场测量就可证实。

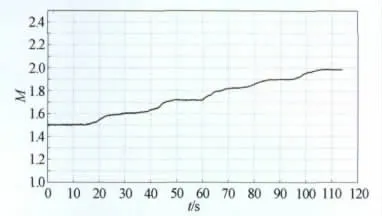
图13 半柔壁喷管变马赫数试验马赫数变化历程（M1.5→M2.0）Fig.13 Time evolution of Mach number（M1.5→M2.0）

图14 半柔壁喷管变马赫数试验马赫数均匀性变化历程（M1.5→M2.0）Fig.14 Time evolution ofσMin test section（M1.5→M2.0）

图15为喷管马赫数从2.5变化到2.0，再从2.0变化到2.5，距试验段入口0.5m试验段中心点的马赫数随时间变化曲线。图16为距试验段入口0.5m水平方向的马赫数均方根偏差，在开始和中心的一段平直曲线的值，分别代表了马赫数2.5和2.0的马赫数均方根偏差。在马赫数变化过程中，大部分曲线值高于开始和中心区的均方根偏差，这说明，在喷管进行变马赫数过程中，试验段的马赫数均匀性比固定喷管型面时的状态要差。

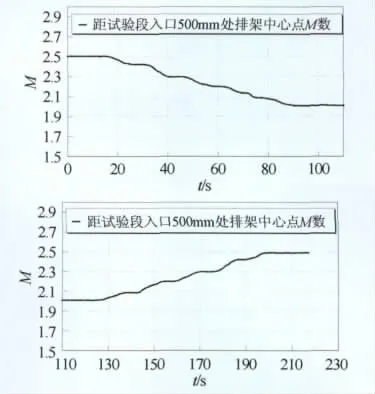
图15 半柔壁喷管变马赫数试验马赫数变化历程（M2.5→M2.0→M2.5）Fig.15 Time evolution of Mach number（M2.5→M2.0→M2.5）

图16 半柔壁喷管变马赫数试验马赫数均匀性变化历程（M2.5→M2.0→M2.5）Fig.16 Time evolution ofσMin test section（M2.5→M2.0→M2.5）

综合上面的分析，可以认为，在喷管进行马赫数变化过程中，只要喷管型面变化速度控制在适当范围，试验段中的流场均匀性与固定型面时的相当。

3 结 论

根据以上的试验结果分析，可得到以下的初步结论：

（a）半柔壁喷管的马赫数变化范围，达到了最高马赫数为3.0的设计指标；

（b）半柔壁喷管第一菱形区内的轴线马赫数均方根偏差，达到并优于d M／M≤1%的设计指标：M＝1.5的均方根偏差为0.0055，超过国军标先进指标；对M＝2.0、2.5、3.0，马赫数均方根偏差分别为0.0098、0.0105、0.0098，接近各马赫数下的先进指标0.007、0.008、0.009；

（c）半柔壁喷管通过动调后，其第一菱形区的马赫数均方根偏差可降低30%～40%；

（d）实现了风洞吹风过程中变马赫数的功能。在喷管进行马赫数变化过程中，试验段中的流场均匀性，在合适的喷管型面变化速度下与固定型面时相当。

［1］ HAROLD N Riise.Design of two－dimension supersonic wind tunnel flexible nozzle［R］.JPL Report No.20－74.

［2］ JAMES C Sivells.Design of two－dimensional continuous－Curvature supersonic nozzle［R］.AEDC－TR－56－11.

［3］ KAWASAKI T.Design of changeable mach number nozzle for blow－down supersonic wind tunnel［C］／／Proc.11th National Congress Appl.Mech.1961：578－584.

［4］ SIEGFRIED F Erdmann.New method for the design of flexible nozzle for the supersonic wind tunnel［J］.Journal of Aircraft，1971，8（1）：385－387.

［5］ ROM J，ETSION I.The development of a single jack flexible nozzle supersonic wind tunnel［J］.AIAA Journal，1972，10（12）：139－146.

［6］ MAC DERMOTT W N.The modification and evaluation to the contour of nozzle［J］.JAS，1955，22（5）：234－240.

［7］ HONSON J R.The evaluation of AEDC－PWT wind tunnel mach number from 1.5to 4.5［R］.AEDC－TDR－63－47.

［8］ MAXWELL H.The correction of supersonic wind tunnel nozzle boundary layer in normalization［R］.AEDCTN－16－153.

［9］ 彭强.半柔壁喷管气动设计关键控制参数研究［J］.空气动力学学报，2011，29（1）：39－46.