涵道共轴多旋翼无人机设计研究

李沂霏 沈志华 王道榆 杨卫东

（南通职业大学，江苏南通 226000）

0.引言

多旋翼无人机作为一种优秀的飞行平台，在民用的诸多领域发挥着举足轻重的作用，从影视航拍到农业植保再到国土测绘，我们几乎可以在各行各业中看到多旋翼无人机的身影。多旋翼无人机凭借其优异的可靠性及操纵性，获得了民用领域的青睐，成为家喻户晓的高科技产品，但与此同时，多旋翼无人机的劣势也在其广泛应用中越来越受到关注。

多旋翼无人机采用螺旋桨作为升力的来源，但螺旋桨无法改变桨距，使得其气动效率低于直升机旋翼，又加上多个螺旋桨相距较近，会产生较为严重的气动干扰，进一步降低了它的气动效率。所以多旋翼无人机的应用主要集中在载重不大、不需要较高气动效率的场景中，对于有较高气动需求或载重需求的场景中，依旧多用无人直升机。但无人直升机结构复杂，操纵困难以及较难维护，又使得其大规模推广受到限制。这种情况下，我们亟需对多旋翼无人机结构进行改进，让其更符合生产生活的需求。

共轴双旋翼直升机自1945 年成功研制以来，历经半个多世纪的发展，共轴双旋翼的理论得到了不断的完善，如今这种构型已经成为一种较为成熟的直升机构型。尽管共轴双旋翼面临着较大的旋翼气动干扰，气动环境复杂，操纵系统复杂等问题，但其上下反转双旋翼的形式，在不增加机体尺寸的同时有效提升了升力，同时也取消了尾桨，有效减少了直升机尺寸，凭借这一优势，多旋翼无人机也越来越多采用此种构型，提升其气动效率。

此外为进一步提升多旋翼无人机的气动效率，在旋翼的外围增加涵道，通过涵道减小不同轴上的气动干扰。

1.旋翼系统设计

1.1 桨叶设计

由于本文主要为验证共轴双旋翼式无人机旋翼系统的可行性，所以在设计时参考了当前多旋翼无人机市场的一些常见机型，尺寸主要参考某知名品牌的植保无人机T20。为了方便验证，翼型选取NACA0012。表1 为桨叶的具体参数。

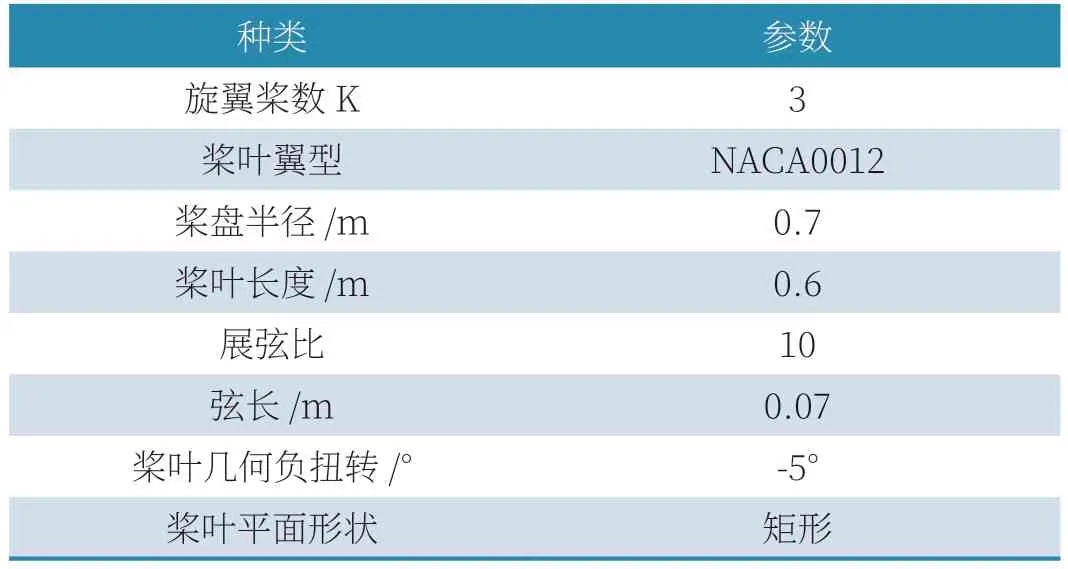
表1 桨叶几何参数

1.2 整体设计

本文中采用四轴的结构形式，单轴上为共轴双旋翼结构，为简化机体结构，上下旋翼分别使用不同的电机控制。在主体结构上增加涵道式外壳，用于减少多旋翼无人机不同轴上的气动干扰。

2.旋翼气动性能计算

本文需要对共轴双旋翼进行气动性能计算，由于共轴双旋翼的结构形式，下旋翼处于上旋翼的尾流中，上旋翼处于下旋翼的滑流中，因此上下旋翼有着较大的气动干扰。为了准确分析旋翼的气动特性，必须纳入气动干扰的考虑。

下旋翼处于上旋翼的尾涡中，导致下旋翼处于较为复杂的气动环境中，因此下旋翼的气动计算较为复杂，而在悬停状态下这种影响最为强烈[1]；下旋翼对上旋翼的影响主要是流态的影响，其影响较小，和单旋翼的状态相差不多。考虑到这些气动干扰，在对共轴多旋翼进行气动分析时就不能使用叶素理论及滑流理论，应采用涡流理论，计入上下旋翼的气动干扰[2]。涡流理论中有固定尾迹、预定尾迹以及自由尾迹的分析方法。固定尾迹认为每片桨叶的环量半径沿半径方向不变，仅有一个涡环柱，在分析时较为简单，一定程度上反映旋翼的涡环状态，但计算的精度不高。预定尾迹采用实验获得的涡环数据，更加贴近旋翼真实的涡环状态，但需提前获取实验数据。自由尾迹采用计算空气动力学计算旋翼的涡环状态，有着较高的计算精度，也不需要提前获取实验数据，但计算量大，计算难度高。本文主要为验证共轴多旋翼无人机的可行性，主要和普通构型的多旋翼无人机比较分析，不需要太高的计算精度且无试验数据，故采用固定尾迹的方法分析旋翼气动特性。

首先建立涡环柱坐标系如图1所示。

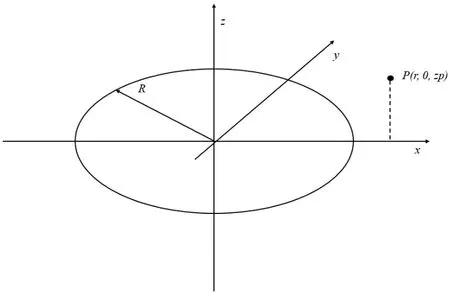
图1 涡环柱坐标系示意图

根据毕奥-萨瓦尔定理可得p点的诱导速度为[3]

本文中，C1，C2的选值为C1=0.99，C2=1.15。对第三类积分精确的计算，采用的是直接积分法。

本文中将桨盘上的涡系离散成有限多个，联合叶素理论推导五个涡柱的表达式为：

式中各诱导速度的系数只和该点到涡柱的相对位置是有关的，因此我们认为这些系数是确定的，对于这个方程组未知量是，显然对于这5个方程来说，是无法解出这6个未知数的，本文采用的方法是给H一个初始值，将方程组变为线性方程组：

求解该方程组，获取5个环量值，根据环量值便可得到任一点的诱导速度，再由求得的诱导速度，可计算得到一个新的H值，设定一个收敛条件，当满足收敛条件时，计算结束。

针对共轴式旋翼系统，可以视为两个单旋翼固定涡系的叠加，因此在计算诱导速度时，要考虑两个涡环柱对该点的影响，因为该点的诱导速度是两个固定涡系的诱导作用总和。

本文计算时，主要考虑旋翼的轴流状态，在该状态下下旋翼只有一部分面积处于上旋翼的滑流里，但上旋翼则完全处在下旋翼的滑流里，在处理过程中，认为共轴旋翼系统的滑流边界和单旋翼结构是一致的[4]，因此，直接使用单旋翼的滑流边界带入到本计算中，进一步减轻计算难度，通过计算验证，发现这样处理带来的误差不大，可以接受。

对于前飞情况，考虑到环量沿方位角变化，将环量表示成Fourier 级数的形式，并取到一阶。

同样，也将诱导速度的表达式也表示成Fourier 级数的形式，也取到一阶。

式中

将环量表达式代入到诱导速度的表达式中，最后便可得到各谐波系数的表达式。最终整理涡环量表达式得到线性方程组为

式中，X= [Γ10…Γ50,Γ11c…Γ51c,Γ11s…Γ51s]T。

通过迭代计算，可得到前进比为0.3 时，上下旋翼的拉力系数。

计算结果如图2 和图3 所示。

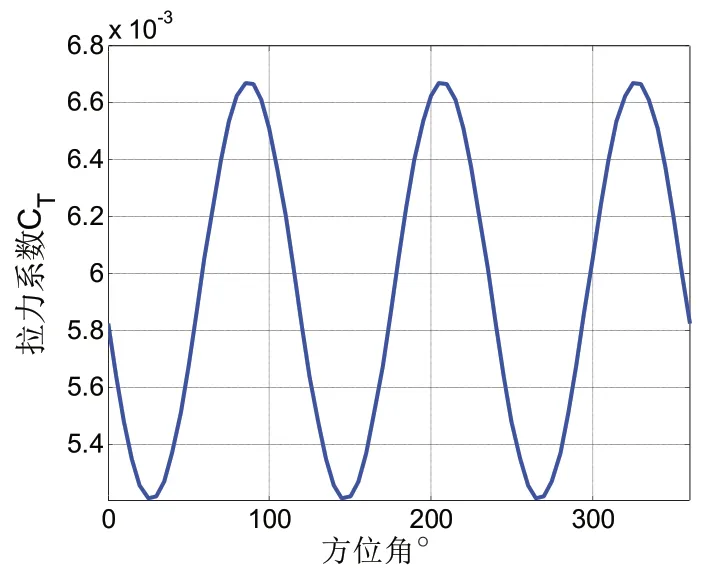
图2 上旋翼拉力系数

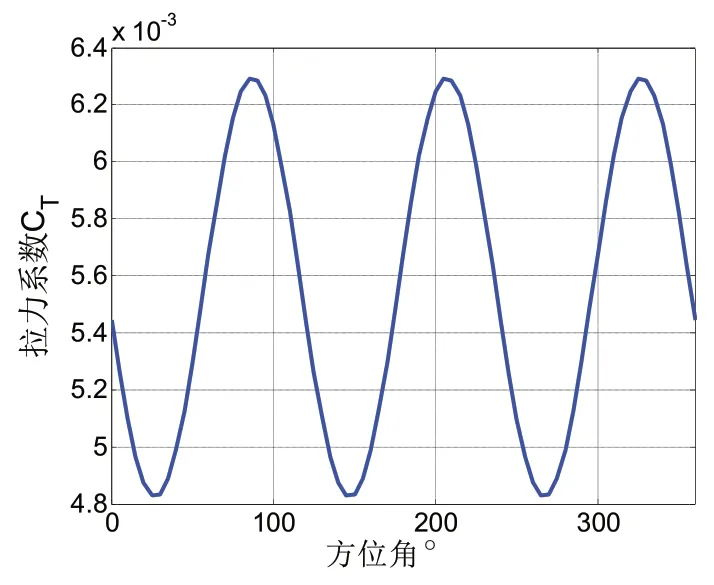
图3 下旋翼拉力系数

根据计算可以看出，多旋翼无人机的拉力有了较大的提升。

3.结语

随着多旋翼无人机的广泛应用，原有的螺旋桨系统由于气动效率较差，越来越无法满足对其性能的需求，本文建立的涵道式共轴多旋翼无人机系统，一定程度上可以解决多旋翼无人机气动效率较差的问题。本文中采用固定涡系理论来对该旋翼系统进行理论计算，具有一定的参考性，未来可使用自由涡系、CFD 等方式进一步验证该方法的有效性。