基于SOLO分类理论中考压轴题思维层次分析及教学策略
胡丰斌

【摘要】中考压轴题可以检测学生解题方式或解题方法,更是对学生思维层次的实证.本文以毕节市2022年中考数学压轴题为例,在SOLO分类理论的指导下进行分析,并提出在课堂教学中注重“四基”,突出思维、注重思维课堂的构建的策略,指出可以通过SOLO分类理论对教学内容、学生思维层次的解读,有效应用知识的逻辑起点即学生最熟练的原有知识进行结构化的表达,培养学生的思维能力,并在教学中有意识地引发学生思考、持续地进行思维训练,达成数学学科核心素养目标.
【关键词】 初中数学;思维课堂;SOLO分类理论
1 “SOLO”理论简介
“SOLO”是英文“Structure of the Observed Learning Outcome”首字母的缩写,意为可观察的学习结果的结构.“SOLO分类理论”是由澳大利亚教育心理学家比格斯(John B.Biggs)和科林斯(Kevin F.Collis)首创的一种以等级描述为特征的学生学习评价理论.“SOLO分类理论”将一个人在回答某个问题时所表现出来的思维结构由低到高划分为五个层次,分别为:前结构、单点结构、多点结构、关联结构和抽象扩展结构.
前结构:学生思维结构处于前结构,回答问题一般表现为拒绝回答、同义反复或胡乱猜测.
单点结构:学生思维结构处于单点结构,只能根据课本中的某个单一事件进行“概括”得出结论,即只根据许多相关点中的某一个点论据就做出解答,所给答案无法自圆其说,或者根本无法给出任何的答案.
多点结构:学生思维结构处于多点结构,有问题线索的意识,在回答问题时,能回答出两个或更多的独立的点,但无法将这些点有机地联系起来,所给的答案往往经不起追问.
关联结构:学生思维结构处于关联结构,根据问题线索,不仅能课本中的知识中找到多个论据,并且能够找到它们之间的内在联系.
抽象扩展结构:学生思维结构处于抽象扩展结构,学生不仅能够利用课本中的知识对某个具体问题进行抽象概括,而且能够结合自己的生活经验、拓展知识等,站在理论的高度来分析问题、解决问题.
SOLO分类理论与思维课堂逻辑关系如图1所示.
2 原题再现
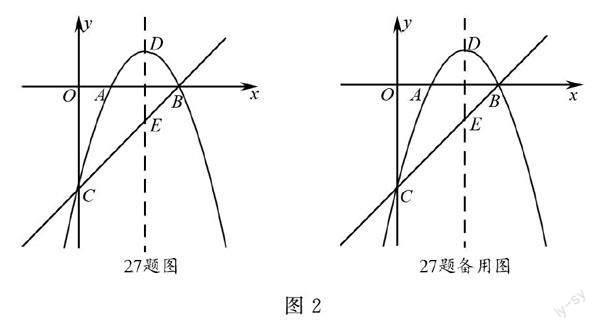
2022年毕节中考27题:(16分)如图2,在平面直角坐标系中,抛物線y=-x2+bx+c与x轴交于A,B两点,与y轴交于点C,顶点为D(2,1),抛物线的对称轴交直线BC于点E.
(1)求抛物线y=-x2+bx+c的表达式;
(2)把上述抛物线沿它的对称轴向下平移,平移的距离为h(h>0),在平移过程中,该抛物线与直线BC始终有交点,求A的最大值;
(3)M是(1)中抛物线上一点,N是直线BC上一点.是否存在以点D,E,M,N为顶点的四边形是平行四边形?若存在,求出点N的坐标;若不存在,请说明理由.
3 基于SOLO分类理论思维层次分析
作为难度逐题加深的压轴题立足于考查初中数学核心知识的同时,也要考查学生运用基础知识的能力与思维发展水平,在发挥压轴题的测试区分度作用的同时,也促进学生解题的灵活性、创新性,让学生在解题中感受数学思想,培养学生的思维能力.该题设问从易到难,循序渐进,也体现了SOLO分类理论单点结构、多点结构、关联结构、抽象拓展结构的思维层次发展.
设问(1)求抛物线y=-x2+bx+c的表达式比较容易,在已知二次项系数为-1与顶点为D(2,1)的情况下学生通过顶点式容易求出y=-x2+4x-3,属于单点结构层次.
设问(2)把上述抛物线沿它的对称轴向下平移,平移的距离为h(h>0),在平移过程中,该抛物线与直线BC始终有交点,求A的最大值.要正确回答本设问需要知道直线BC的表达式,学生通过观察图形知道B、C两点分别在x轴、y轴上,从而分别令纵坐标、横坐标为0得出B(3,0)与C(0,-3),对求出直线BC的表达式不是太难,属于单点结构与多点结构.求出直线BC的表达式后学生需要关联空间想象力并设平移过程后的抛物线y=-x2+4x-3-h,并根据问题线索,联想到方程的思想并找到函数与方程的内在联系,最后转化成一元二次方程实数根的判别式即得解.此题属于关联结构层次.
设问(3)M是(1)中抛物线上一点,N是直线BC上一点.是否存在以点D,E,M,N为顶点的四边形是平行四边形?若存在,求出点N的坐标;若不存在,请说明理由.
此问题属于抽象拓展结构层次.不仅只是集中于一个知识点的掌握,而是具有综合性,集结论猜想型、运动变化型、函数应用型于一体.学生解题时也要综合考虑分类讨论的、数形结合、待定系数法、解一元二次方程等思想与方法.通过解决此问题可以培养学生的运算能力、想象能力、推理能力,其本质上是培育学生数学核心素养,落实2022版新课标要求.
4 基于SOLO分类理论的教学策略
策略是指在一定条件下,为达到设定目标所采用的方式、方法、媒体的总和.教学策略是指在教学过程中遵循一定的教育思想和方法,在知识目标与素养目标的导向下,依据教学的主客观条件,特别是学生的实际情况,对所用的教学顺序、活动程序、组织形式、教学方法和教学媒体等的总和.本文对毕节市2022年初中升学考试数学卷压轴题的SOLO分类理论分析,探讨学生思维层次变化与在初中数学教学中培养学生数学核心素养的教学策略.
第一,充分遵循学生身心发展规律,发展素质教育是利用“SOLO分类理论”分析学生思维层次的基础.新时代的教育本质是坚持五育并举,落实立德树人根本任务.初中数学教育必须遵循教育规律,发展素质教育,对压轴题解法教授最好的方法是尊重学生身心发展特征、引导学生循序渐进、克服畏难情绪,让学生从不敢接触到逐渐尝试.教师一定要从平常幽默诙谐的教学中、从平常寓教于乐中加强学生身心健康的理解,必要时进行疏导,让学生平时在素质教育的实施中掌握数学知识与技能、数学方法与思想,升学考试时对压轴题的解答就没有畏难情绪,为压轴题结题思维的打开扫清障碍.
第二,利用“SOLO分类理论”思维层次在课前预判学生在学习过程中思维层次,为思维课堂的建构做充分、得当的准备.对参加初中升学考试的学生思维层次对应压轴题一般是三个分问题.第一个分问题比较容易解决属于单点结构层次,有八成学生都能够回答,第二个分问题属于常规题型,相对比较难,属于多点结构与关联结构,学生有六成到七成能够回答,第三个分问题更难,一般属于抽象拓展结构,对学生的数学解题能力要求更高,只有三成以下的得分率.还要针对压轴题起点低,难度小,尾巴略微高的状态,关注不同思维层次的学生在解题过程中可能出现的思维变化特征,引导学生在平时练习中要能够适应数学压轴题的梯度,并尝试寻找解决的方法,争取在初中数学升学考试中提高解题能力,让学生的压轴题数学均分逐步提升,促进学生思维层次的提高.
第三,情境创设激发学生学习兴趣,搭建学习脚手架.教学中教师要充分了解学生学情、评估思维发展水平的基础上,创设情境,有效组织学习材料内容与呈现方式、抓住学习材料的内在本质特征和先前知识经验,找准学生的最近发展区,营造轻松的学习氛围,把学生从前结构学习水平自然过渡到单点结构学习水平,有效地解决在单点结构层次问题.
第四,问题引导促使学生积极思考,逐步提高学生的思维水平从单点结构向多点结构发展.引导学生思考,逐步提高学生的思维水平从单点结构向多点结构发展.教学中教师在教学设计过程中利用SOLO分类理论分析影响学生的思维水平,积极促进学生各种能力从低级层级发展到更高的层级,在轻松解决单点结构层次问题的同时,实现教学目标并引导学生思维水平向多点结构发展.
第五,探究解析潜移默化影响学生数学思维,促使学生思维从多点结构向关联结构发展.压轴题的求解是学生思维发展的训练,在数学学习中尤为重要,我们常说“一题多解”便是这个道理.通过平时教学中循序渐进地训练难度适中,绝大多数学生都敢做的基础题型,由浅入深,由简到繁,让学生经历探索数学基础知识、基本技能、基本思想、基本活动经验知识的过程,引导学生探究解析自主摸索压轴题的解题技巧途径,提升学生在升学考试中解题方法的迁移能力,使不同思维水平的学生根据已知的规律都能打开新的思维,充分发挥自己的能力,最大限度思维达到关联结构水平.
第六,建构反思促进学生思维的思维进阶.学生在经历了探究解析的过程后,对解题方法和规律的概括已经相当成熟,但要真正理解所学知识,同时发现问题、提出问题、分析问题、解决问题的能力还需要在反思中巩固,顺势引导学生思维向抽象拓展结构层次进阶.
第七,迁移拓展发展科学精神、应用意识和创新意识,培育学生数学核心素养.压轴题的解决不应该只是一味地让学生做题目,而应该从学生做过的题型出发,提升学生的运算能力、推理能力.通过学生经历数学问题解决的思维过程,巩固理解数学的基本概念和法则,并加深数学思想的实践应用、数学与现实世界之间的联系,会用数学眼光观察现实世界,并用数学思维分析、解决简单的数学问题和实际问题,发展质疑问难的批判性思维,形成实事求是的科学态度,在培养学生数学应用意识的同时初步养成良好的思维品质,发展学生创新精神,促进数学核心素养的形成.
5 结语
总之,压轴题之所以为压轴题,就是因为可以检测学生解题方式或解题方法,更是对学生思维层次的实证.这就要求教师在教学中注重“四基”,突出思维、注重思维课堂的构建,通过SOLO分类理论对教学内容、学生思维层次的解读,有效应用知识的逻辑起点即学生最熟练的原有知识进行结构化的表达,培养学生的思维能力,并在教学中有意识地引发学生思考、持续地进行思维训练,达成数学学科核心素养目标.
【基金项目:本文为2021年贵州省教育科学规划课题《基于SOLO分类理论指导下的初中数学思维课堂建构与实践研究》(课题编号:2021A026)阶段成果】
参考文献:
[1]范强华.基于SOLO分类法谈初中数学复习课教学[J].数学教学通讯,2021,(20):3-4+10.
[2]范雪晨,吴利敏,王罗那.SOLO分类评价法在初中数学教学中的应用[J].湖州师范学院学报,2022,44(04):101-105.
[3]陈琳.基于SOLO理论的初中数学试卷讲评课的教学研究[D].杭州师范大学,2018.
[4]赵玉華.初中数学抽象思维的教学层次与知识体系[J].现代中学生(初中版),2021(18):3-4.
[5]肖代林.擦出思维火花 深化课堂探究——初中数学课堂思维的提升[J].试题与研究,2020(20):136.

