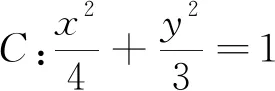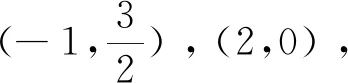利用极点极线探究从“圆”开始的定点问题

广东省汕头市澄海中学 (515800) 林建群 陈焕涛

在圆锥曲线问题中常常考察定点定值问题,很多定点定值问题隐藏在相关几何关系中.圆具有完美的对称性以及丰富的几何性质,我们可以考察圆的相关问题,再猜想其在一般圆锥曲线中的相关结论.本文以一道圆中的定点问题为起点,利用极点极线理论发掘一般圆锥曲线中的定点问题.

一、试题的分析与求解

题目过直线x+y=4上一动点M,向圆O:x2+y2=4引两条切线,A,B为切点,求圆C:(x+3)2+(y-3)2=1上的动点P到直线AB距离的最大值.(华中师大一附中2021-2022学年高二期考题).

分析:本题有两个难点,一是求解直线AB的方程,二是动点到直线的距离问题.本题涉及到的直线与点都是运动的,本题的解题关键则在于发现运动中的不变性.

解析:设点M的坐标为(x0,y0),设切点A,B的坐标为(x1,y1),(x2,y2),设过点A的切线方程为lA,根据圆的几何性质可得OA⊥lA.结合点A的坐标可得切线方程lA为x1x+y1y=4.因为点M∈lA,可得x1x0+y1y0=4(1).同理可得x2x0+y2y0=4(2).为此构造直线l:x0x+y0y=4,由上两式可得A∈l,B∈l,即可得直线l即为直线AB.因为点M在直线x+y=4上,可得x0+y0=4,代入直线l可得x0(x-y)+4y-4=0,所以该直线过定点N(1,1).

反思:在本题中出现了两个圆,直线AB为圆O的切点弦,其主要意义在于发现直线AB过定点.圆C的意义在于求解最值,而圆O也可承担圆C的功能,所以此题略显复杂.

笔者认为可以将原问题改编如下:

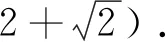
笔者在求解该问题后,再提出了如下的思考:(1)在本题中出现的直线x+y=4,圆O:x2+y2=4以及定点N(1,1)三者有什么必然联系呢?(2)当将圆转化为其他的圆锥曲线时,是否存在这样的定点呢?

二、问题的本质探究

极点极线的几何定义[1]:如图1,P是不在圆锥曲线上的点,过点P引两条割线依次交圆锥曲线于四点E,F,G,H,连接EH,FG交于N,连接EG,FH交于M,则直线MN为点P对应的极线.

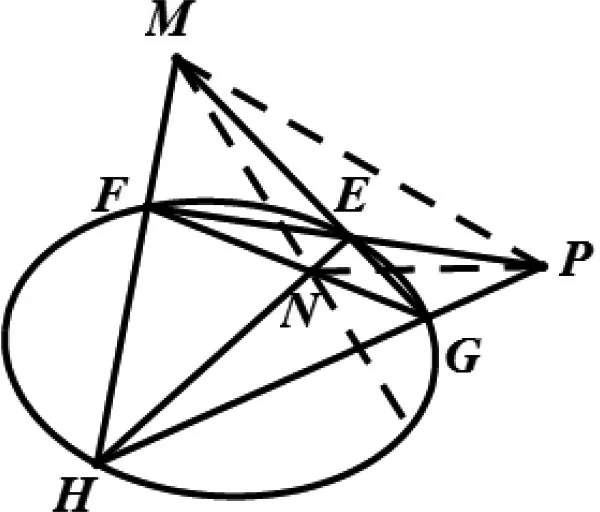
图1

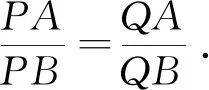
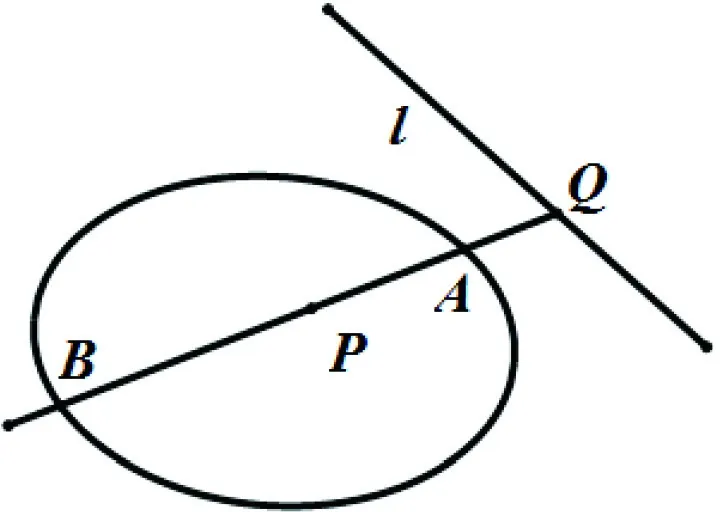
图2

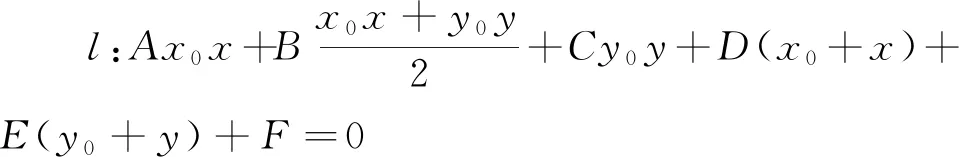
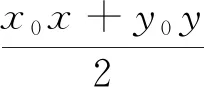
特别地对于高中常用的圆锥曲线:

(1)圆(x-a)2+(y-b)2=r2,点P(x0,y0)对应的极线方程为(x0-a)(x-a)+(y0-b)(y-b)=r2;

(4)抛物线y2=2px,对应的极线为y0y=p(x0+x).

极点与极线的基本性质:

定理2(1)当点P在圆锥曲线Γ上时,其极线l是曲线Γ在点P处的切线;(2)当点P在Γ外时,其极线l是切点弦所在的直线;(3)当点P在Γ内时,其极线l是过点P的弦两端点的切线的交点所构成的集合;

定理3 (配极原则)点P关于圆锥曲线Γ的极线p经过点Q,点Q关于Γ的极线q经过点P;由此可知,共线点的极线必共点;共点线的极点必共线.

回到上文中的问题应用上述极点极线的结论可得:点M与直线AB(切线弦)即为一组极点极线;根据上述配极原则,我们可知点N(1,1)与直线x+y=4也是关于是圆O:x2+y2=4的一组极点极线.

三、一般圆锥曲线中的结论

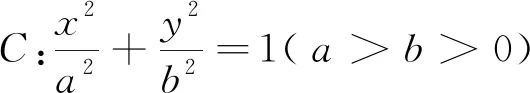
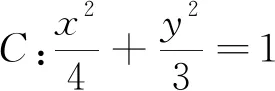
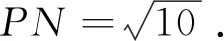
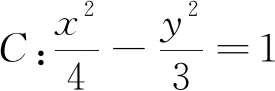
例3 过直线l:2x-y+4=0上一动点M,向抛物线C:y2=4x引两条切线,A,B为切点,求点P(-1,0)到直线AB距离的最大值.

注意到上述问题中出现的点P均是一个定点,当曲线为双曲线及抛物线时,当点P为动点时,对应的距离的最大值不存在;当曲线为椭圆时,存在最大值,但表达式过于复杂,本文不再探究.

接下来,我们通过特殊化来研究椭圆条件下的最大值问题.

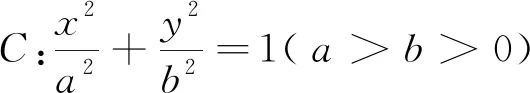
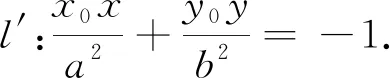
根据该定理,即可命制出如下问题: