一道向量面积比问题的探究

江苏省苏州市张家港市外国语学校 (215600) 董文娟

1 试题呈现

.

2 解法赏析

思路1:基底法

基底法是解决向量问题的常见方法,选定平面的一组基底后平面内任意一个向量都可以用其线性表示,从而化为基底向量减少未知量,将问题简化.基底法一般会结合向量的基本定理,从数形结合角度去理解问题,综合考查学生的数学建模能力,数学运算能力等.

图1

评注:三角形中选择相邻两边作为一组基底,将其他向量都用该基底线性表示,根据平行四边形法则,构建平行四边形得到边的关系,从而得到三角形面积关系.

思路2:坐标法

向量和坐标一一对应,因此对于向量的问题除了直接利用向量解决,还可以考虑从坐标入手.根据题目特点,本题除了一般的建系方法外,还可以利用特殊位置特殊点来简化坐标,减少运算.

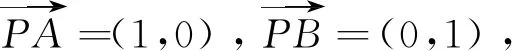
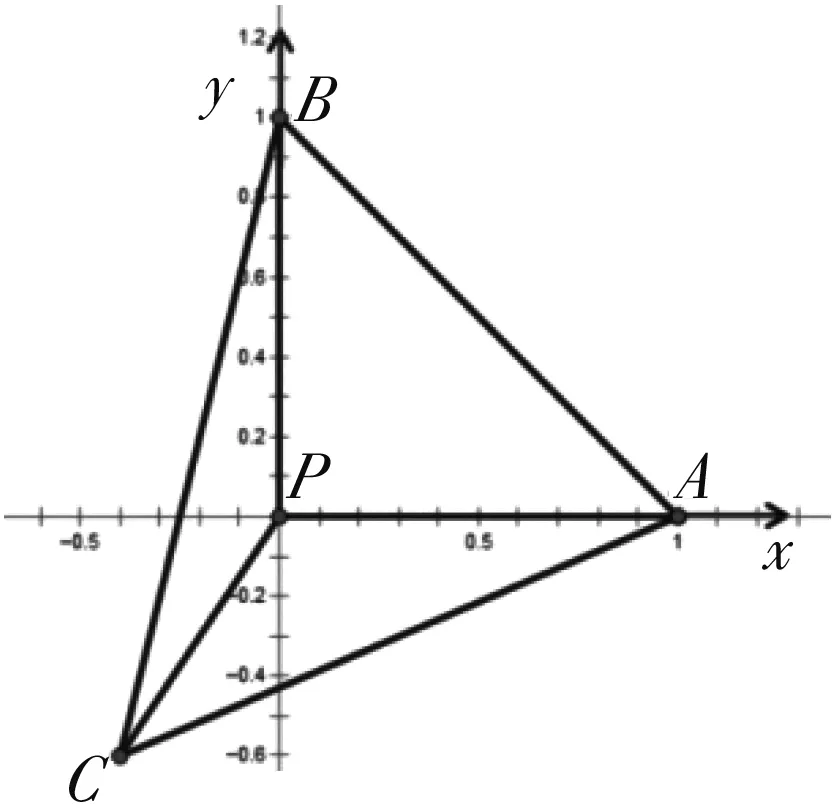
图2

解法3:(特殊图形)如图3,不妨取ΔABC为直角三角形,且取A(0,1),B(0,0),C(1,0).设

图3

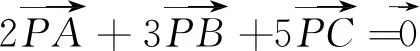
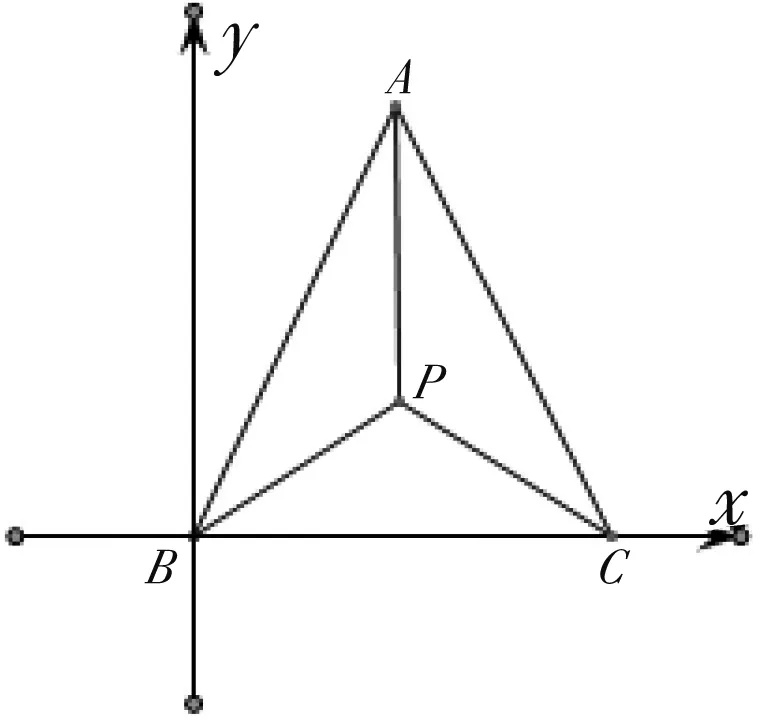
图4

评注:坐标化后向量问题数量化,向量问题转化为坐标运算问题.对图形或者点位置没有具体要求的问题,可将条件特殊化再建系.

思路3:等和线定理

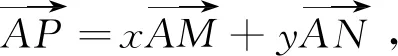
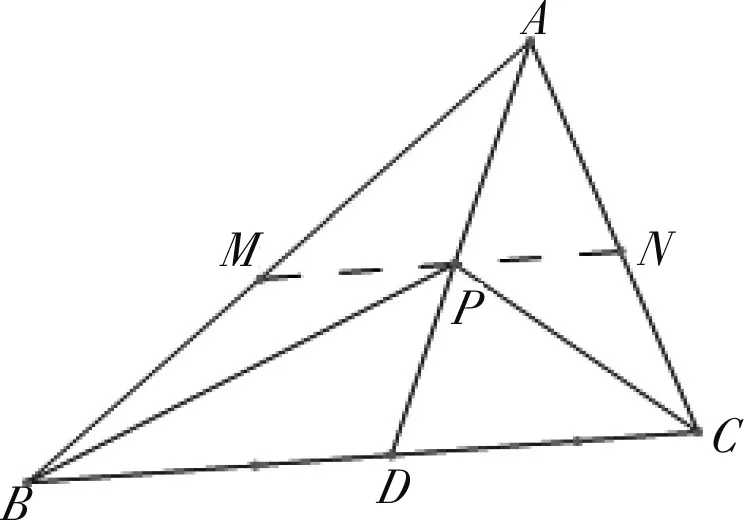
图5

评注:在平面向量基本定理的表达式中,如果需要研究两系数的和时,可以用等和线法.根据等和线定理,得到三角形边的关系,由边的关系可得到面积关系.

思路4:综合几何法

对向量的比例关系,从图形上探求三角形的边之间的关系,从而得到面积之间的关系,体现数形结合解题的优势所在.

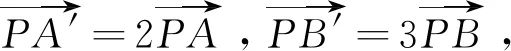
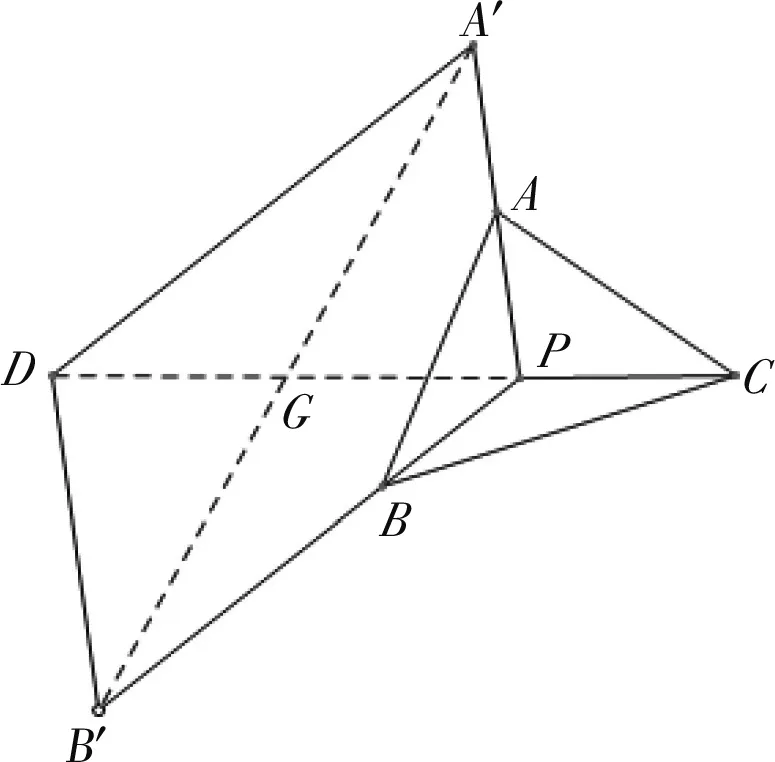
图6

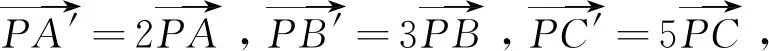
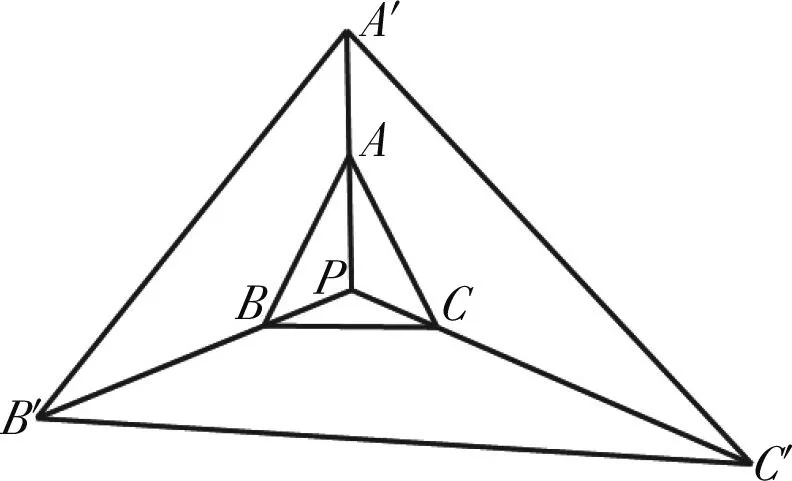
图7

评注:几何法从图形上直观分析面积比关系,不用大量的定量计算,对平面几何知识要求较高.

利用系数关系构造新的三角形将点P位置特殊化为熟悉的重心,利用三角形面积公式,将面积比转化为边之比.

思路5:平面向量的外积

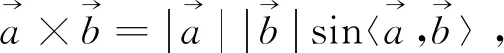
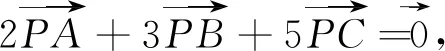
评注:平面向量的外积运算,可以运用在求三角形的面积问题中,在此考虑外积的大小不考虑其方向,要熟知外积运算的性质.

思路6:奔驰定理法

向量的奔驰定理揭示了三角形的面积和向量之间的关系,对于解决三角形的面积比问题,空间四面体的体积比问题等都适用.

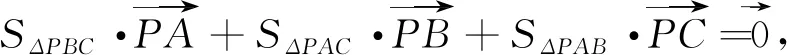
评析:奔驰定理的证明可以参考解法8,奔驰定理可以迅速的解决该面积比问题.对于点P在三角形外的问题,点P为三角形的四心问题,及对于空间四面体的问题也由相应的推广[1].

3 简单应用

3.1 变形求面积比

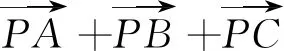
3.2反求向量式系数问题

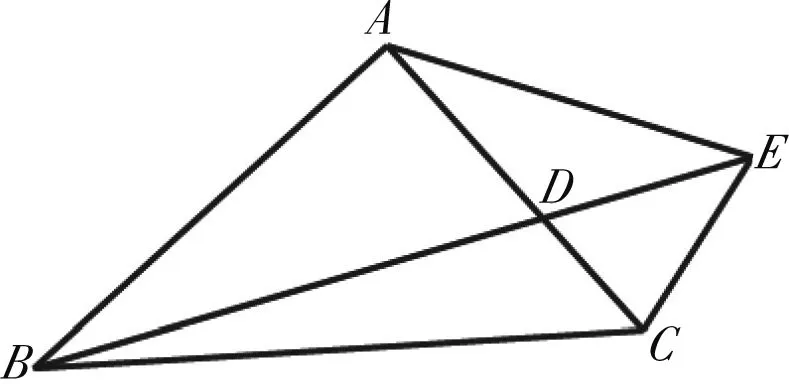
图8

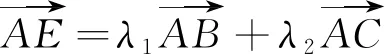
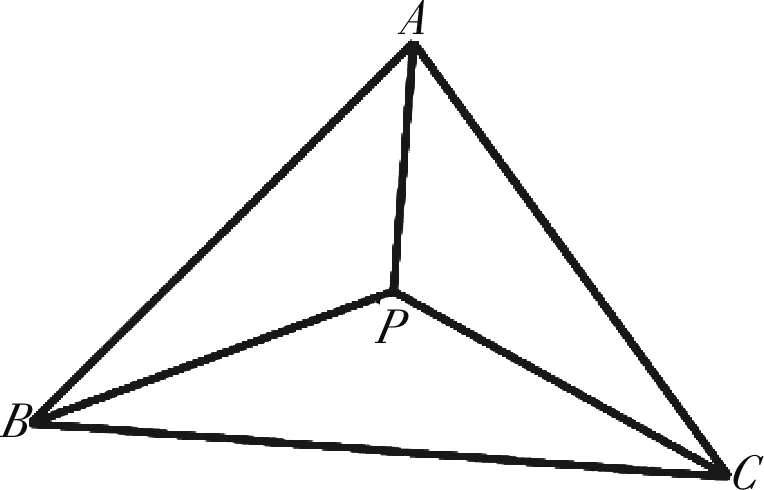
图9

评注:点P在三角形内或者三角形外,三角形面积都有类似的结论,根据向量关系先得到点所在位置,利用对应的面积和系数比关系得到结果.逆向思维可以由面积比得到系数之比,从而得到向量的系数关系.遇到向量的系数问题,结果图形考虑是否可以利用三角形的面积比问题.

4 小结

向量因其独特的双重性,在解题中灵活多变的思路,成为学生惧怕的对象.对于面积比问题的多解分析,更加透彻理解面积比问题的处理,从而对一些向量式的系数问题模式化.

对一题多解,在教学中不可一刀切只讲一种方法,也不可面面俱到,应呈现给学生一些有价值的想法,达到对问题的深刻理解,对问题考查方式的全面理解,对解法的灵活运用,从而对问题更加全面的思考.通过一题多解,归纳多题同解,让学生对数学背景,数学知识,数学思想方法深入理解.从一个有意义且不复杂的题目去挖掘各个方面的信息,从一道题领悟无线道题的可能.