关注知识生成 渗透数学思想——以“平均变化率”的课堂教学为例

江苏省兴化市楚水实验学校 (225700) 邹勇泉 袁小强

数学概念教学在数学教学中处于核心地位,概念学习过程是一个探究的过程.近期笔者有幸参加了江苏省第十七届“蓝天杯”课堂教学展评课,展示了一节“平均变化率”教学课,授课对象是普通高中高二学生,本文结合苏教版普通高中教科书《数学》选修(2-2)第一章“导数及其应用”第一课时“平均变化率”的教学设计谈谈关注知识生成,渗透数学思想,帮助学生构建探究一般数学概念的方法.

本课时的内容是平均变化率,变化率包括平均变化率和瞬时变化率,平均变化率是研究瞬时变化率和导数的基础,经历位移的变化、速度的变化、曲线的上升与下降等具体想象,抽象出研究函数的改变量和变化率等数学理论.通过实际背景和应用实例引导学生经历由平均变化率到瞬时变化率的过程,从而认识和理解导数的概念和本质.

一、课堂教学实录

1.创设情境,问题导入

世界充满着变化,有些变化几乎不被人们所察觉,而有些变化却让人们发出感叹与惊呼.

情境1播放歌曲《可可托海的牧羊人》,《Mojito》.感受这两首春晚热门歌曲旋律节奏有何不同?

(初步感受节奏变化不一样,第一首节奏变化慢,第二首节奏变化快)

情境2某市4月20日最高气温为33.4℃,而4月19日和4月18日的最高气温分别为24.4℃和18.6℃,短短两天时间,气温陡增14.8℃,闷热中的人们无不感叹:“天气热得太快了!”

时间4月18日4月19日4月20日日最高气温18.6℃24.4℃33.4℃

该市3月18日到4月18日的日最高气温变化曲线,如图1:

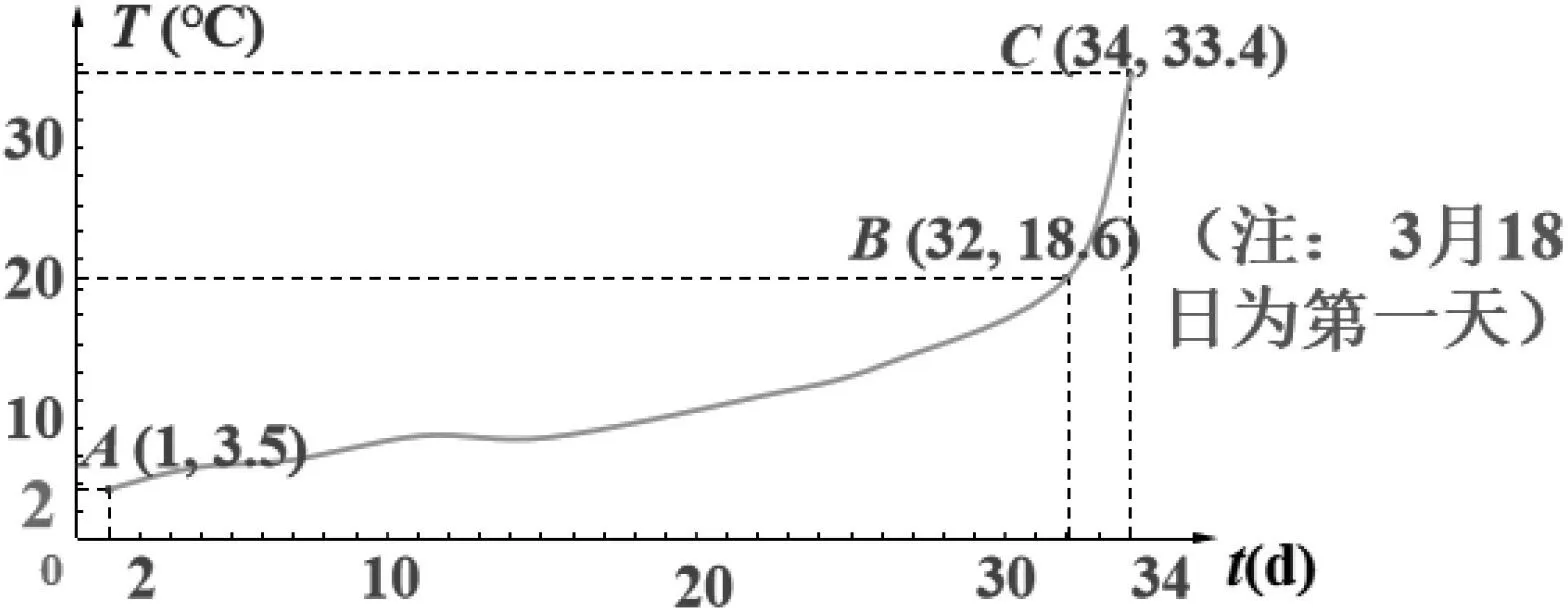
图1

设计意图:通过图片、音乐、文字、表格、图象展示,让学生感受到生活中存在大量“变化快慢的量”,激发学生的学习兴趣,体现数学教学的美育价值.

2.新课探究,学生活动

问题1 你能说出图1中A、B、C三点的坐标所表示意义吗?

问题2 你可以分别计算AB、BC段温差吗?可以用数学语言解释一下“天气热得太快了”吗?(从数与形两方面)

小结:气温差不能反映气温变化的快慢程度.

问题3 如何“量化”(数学化)曲线AB、BC的陡峭程度呢?(小组合作讨论)

生:不好直接研究曲线AB、BC的陡峭程度,只能“大致”研究.

追问:怎么“大致”研究呢?

生:只能研究线段AB、BC的陡峭程度.

追问:如图2,如何研究线段AB、BC的陡峭程度呢?我们前面研究过如何刻画线段或者直线的陡峭程度吗?

图2

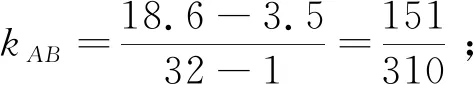
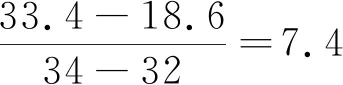
问题4你能用数学的语言来表达一下:曲线上升的陡峭程度吗?(从数与形两方面)

设计意图:通过问题串的设置,在自主探究、小组合作、师生互动中, 抓住学生有价值的知识生成,展开教学.通过问题2引起学生的认知冲突,通过讨论,让学生得到结论:气温差不能反映气温变化的快慢程度.通过问题3的讨论,找出研究“陡峭程度”的数学方法,会用数学语言来表达世界,为得出函数平均变化率概念提供了案例基础.

3.数学建构,形成概念

我们通过分析气温的变化的图象,研究了气温的变化情况,思考:

问题5已知函数y=f(x),从x1到x2的平均变化率如何计算?由此,你能总结出求函数平均变化率的一般步骤吗?

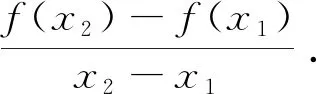
问题6函数平均变化率的几何意义是什么?

如图3,平均变化率是曲线陡峭程度的“数量化”,曲线的陡峭程度是平均变化率的“视觉化”.用平均变化率量化一段曲线的陡峭程度是“粗糙不精确的”,但应注意当x2-x1很小时,这种量化便由“粗糙”逼近“精确”.

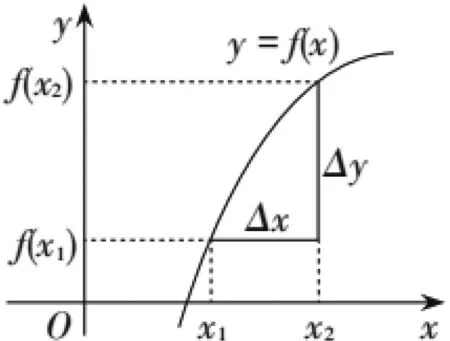
图3

图4

设计意图:从实例探究抽象出一般性函数问题,通过问题5抽象概括出函数平均变化率的一般定义,问题6通过分析函数和图象两个角度理解平均变化率的意义.

4.数学运用,深化概念

课堂练习1:某婴儿从出生到第12个月的体重变化如图5所示,试分别计算从出生到第3个月与第6个月到第12个月该婴儿体重的平均变化率,由此你能得到什么结论?

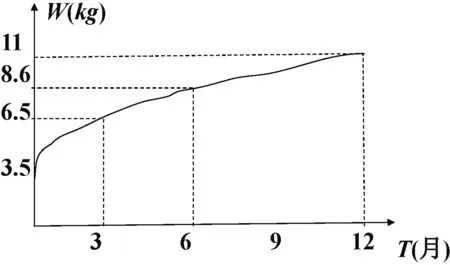
图5

例1 如图6,水经过虹吸管从容器甲中流向容器乙,ts后容器甲中水的体积V(t)=5e-0.1t(单位:cm3),试计算第一个10s内V的平均变化率.

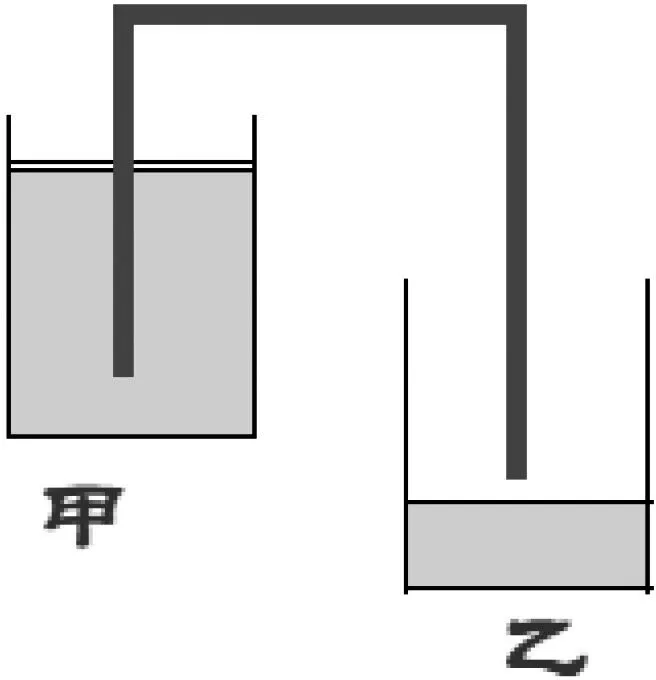
图6

课堂练习2:已知函数f(x)=x2,分别计算函数f(x)在区间[1,3],[1,2],[1,1.1],[1,1.001]上的平均变化率.

例2已知函数f(x)=2x+1,g(x)=-2x,分别计算函数f(x)及g(x)在区间[-3,-1],[0,5]上的平均变化率.

思考:从上例中,你能发现一次函数y=kx+b在区间[m,n]上的平均变化率有什么特点吗?

设计意图:练习1和练习2是函数平均变化率的简单应用,检验学生在不同情境中对平均变化率的理解,例1通过在新情境下,帮助学生理解平均变化率的实际意义,例2和思考,通过由特殊到一般的数学归纳的思想方法,从而进一步帮助学生理解平均变化率的几何意义.

5.课堂小结,总结提升

本节课你学到了什么?你可以从基本知识,基本技能,基本数学思想方法等不同的角度谈谈.

设计意图: 关注学生在课堂中的学习体验中学到了哪些,让学生从基本活动经验的学习过程中有所收获,有所得,可以从基本知识,基本技能,基本数学思想方法等不同的角度谈谈自己的收获.

二、教学思考

1.问题驱动,促进概念生成

数学是各类科学中最抽象的科学,张奠宙教授提出:知识的基本形态分为知识的科学形态和知识的教育形态,也就是知识的发生形式和知识的呈现形式.问题是数学的心脏,因此教学中需要把知识发生形式的过程转化为一系列带有探究性的问题,使学生学会思考,使概念学习变为学生内在需求.同时问题的设计要充分了解学生的认知水平和心理发展特点,注意选择新颖有趣的活动作为刺激模式,激发学生主动观察、思考、归纳、总结,积极开展探究活动.通过情境1两首不同的歌曲刺激学生思考它们的不同属性,情境2通过“温度变化曲线图”感受气温变化的快慢,教师适时提出一系列的探究问题,让学生借助这些“脚手架”讨论如何研究变量变化的快慢,再结合前面所学的直线斜率相关知识形成“平均变化率”的概念.

2.五育并举,自然融入课堂

良好的审美素养影响人对社会、对他人、对事物积极的人生态度,同时良好的审美素养对培养人的创造能力也十分重要.开头过山车的图片,情境1的音乐设置,使学生学会用数学的眼光度欣赏美,让学生开阔视野,感悟实际中的美,数学中的美,激发学生培养艺术素养,培养数学学科素养,从而让学生会用数学的眼光欣赏世界的美,会用数学的思维思考世界的美,会用数学的语言表达世界的美.

3.数形结合,渗透数学思想

认知心理学家罗斯认为,记忆中的概念是以这些概念的具体实例来表示的,而不是以某种抽象的规律或一系列相关特征来表示的.本课的实例“气温变化曲线图”在学生的知识形成过程中起着重要的作用,“气温变化曲线图”也就是学生 “平均变化率”的意象表征或心理表征,于是学生在生成“平均变化率”概念过程中,自然渗透了数学结合、转化与化归等重要的数学思想,以形解数,以数助数,形成研究数学问题可以从数形两个角度寻求两者之间的内在联系,使得两者在认识结构中共存,以后在适当时机发挥重要的作用,在概念形成过程中渗透数学思想,润物细无声.