边角关系共纠缠 基底法则来解难——对2022年南昌一检理第12题的求解

福建省福清第三中学 (350315) 何 灯

试题呈现已知点A(-1,0),B(3,0),P是圆O:x2+y2=45上的动点,则sin∠APB的最大值为( ).

上述试题以圆为载体,考查三角形中的边角关系;考查推理论证能力、运算求解能力;考查直观想象、逻辑推理、数学运算等核心素养.由于P点位置的不确定,且所铺设的条件无法直接转化为∠APB,导致用正余弦定理求解本题较为困难.

借助于余弦定理及导数工具,有解答过程:

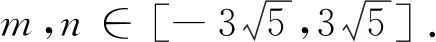
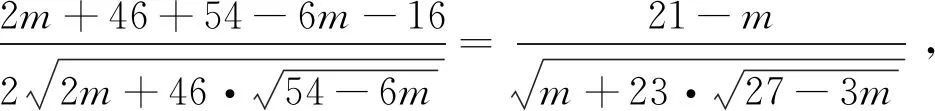
上述过程的求解思路较为自然:设点、求边、余弦定理求角、化sin∠APB为m的函数、求导寻最值,但整个过程运算量较为庞大,大部分同学无法顺利完成.本题是否有其他较为简洁的求解方法?

解析二:显然,要使sin∠APB取最大值,点P不能在x轴上.

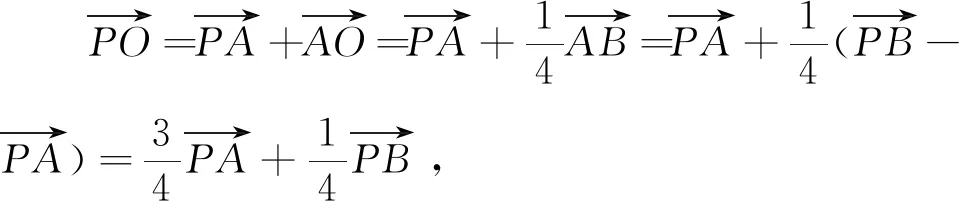
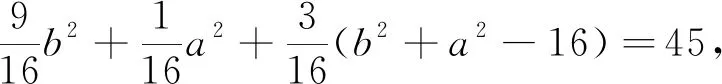
通过平面向量基本定理和基底法则,上述求解过程建立起分线长与三角形的边角之间的联系,进而借助余弦定理及基本不等式,实现了问题的轻松求解,体现了化归与转化思想、数形结合思想和方程思想在问题求解过程中的引领作用.类似于上述过程,还可实现试题结论的一般性拓展,此留给有兴趣的读者继续探究.