一道中考压轴题的多种解法

文／黄学维

原题呈现 （2022 年苏州中考第8 题）如图1，点A的坐标为（0，2），点B是x轴正半轴上的一点，将线段AB绕点A按逆时针方向旋转60°得到线段AC。若点C的坐标为（m，3），则m的值为（）。

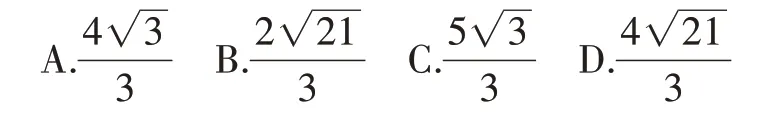
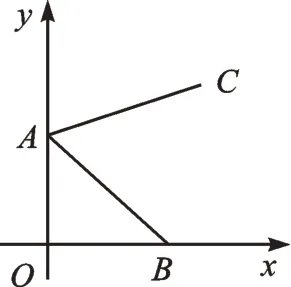
图1

这是一道选择压轴题，图形简单，但很难入手。如果我们细细品味一番，会发现别有一番滋味，值得深入研究。

一、利用两点之间距离公式，建立方程（组）求解

解：连接BC，如图2。

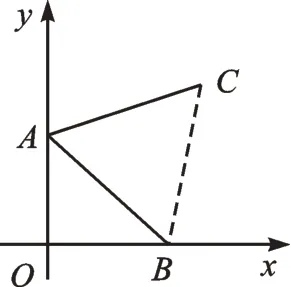
图2

设点B坐标为（a，0），由旋转得△ABC是等边三角形，得AB=BC=AC。

∴a2+4=（m-a）2+9=m2+1。

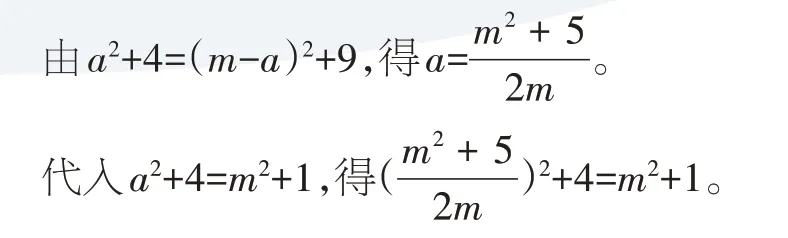
整理，得3m4-22m2-25=0。

∴（3m2-25）（m2+1）=0。

用勾股定理很容易得到平面直角坐标系下两点之间的距离公式。这个公式在很多问题中弱化了构图，而其本质还是构造直角三角形，利用勾股定理求解。

二、利用矩形框“斜向三角形”，建立方程解决问题

解：连接BC，过点C作CD⊥x轴于点D，CE⊥y轴于点E，如图3。

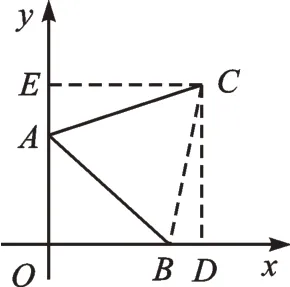
图3

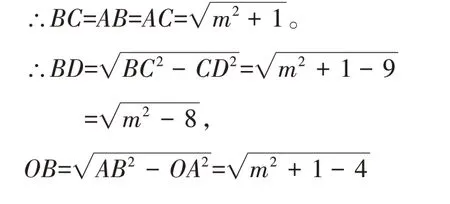
易得OA=2，AE=1，CE=OD=m，CD=3。由旋转得△ABC是等边三角形，

整理，得3m4-22m2-25=0。

∴（3m2-25）（m2+1）=0。

三、巧用图形的旋转构造特殊三角形，利用三角函数求解

平面坐标系中处理“斜向三角形”（三条边均不与坐标轴平行或重合）问题的常用方法是用矩形将目标三角形框起来，然后根据勾股定理计算相关的线段，利用线段的和、差列方程解决问题。但是这个方程是无理方程，我们可以通过两边同时平方的方法得到一个4 次方程，再运用因式分解分成两个2 次方程，这对计算能力要求较高。

前面两个方法的共性是思维难度低，但计算难度高。因此，我们在平时的学习和备考中不能忽视计算能力的培养。

解：过点A作y轴的垂线，过点C作x轴垂线，两线相交于点D，将△ACD绕A点顺时针旋转60°得△ABE，设AE交x轴于点F，如图4。

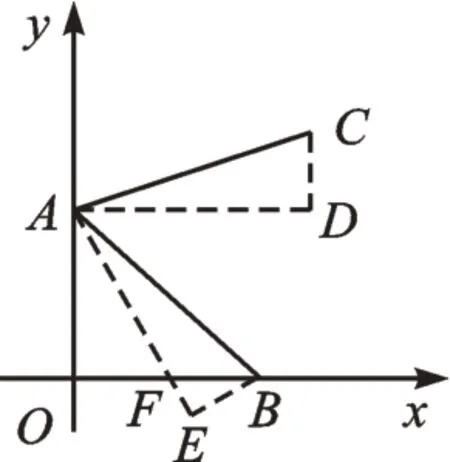
图4

根据题意，容易得到BE=CD=1，AD=AE，∠OAE=90°-60°=30°。

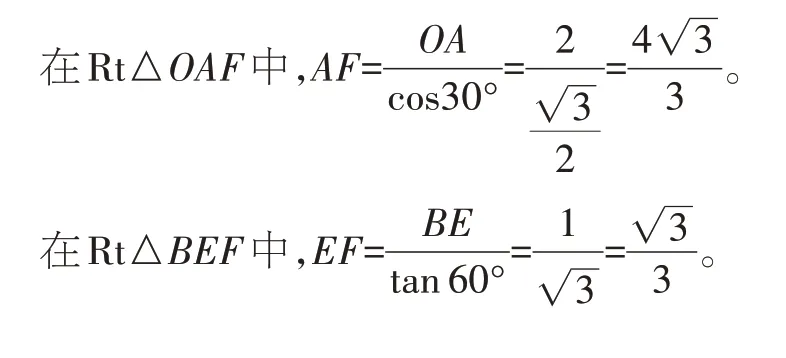
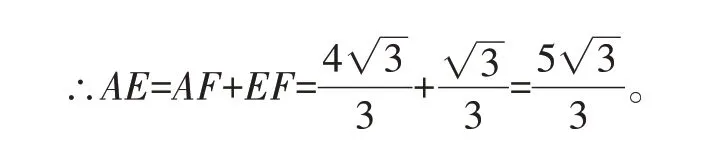
四、巧妙构造外接圆，通过解直角三角形求解

解：连接BC，作△ABC的外接圆交x轴于另一点D，连接AD、CD，作CE⊥x轴于点E，如图5。

图5

由旋转可知△ABC是等边三角形。

∵∠ADC=∠ABC=60°，∠BDC=∠BAC=60°，

∴∠ADO=180°-∠ADC-∠BDC=60°。

在Rt△ADO中，OA=2，∠ADO=60°，

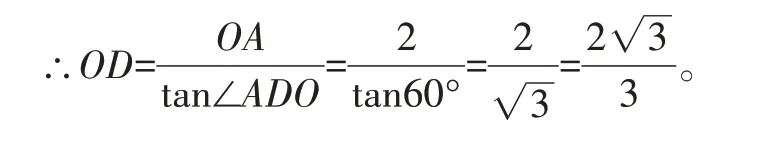
在Rt△DCE中，CE=3，∠CDE=60°，

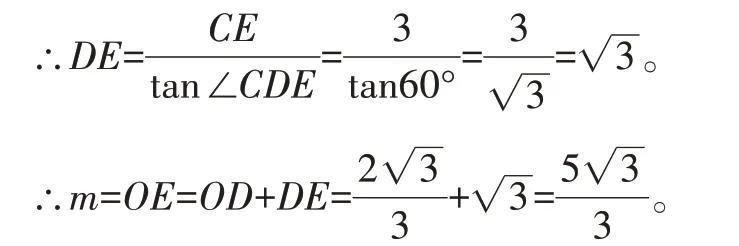
构造△ABC的外接圆，由同弧所对的圆周角相等可巧妙求出∠ADC，再构造Rt△ADO和Rt△DCE，求出OD和DE，从而求得OE。该方法构造是前提，在充分运用圆的性质基础上，灵活运用了知识之间的内在关系。

在平时的学习中，我们要不断积累解决综合题的方法和技巧，学会用代数和几何的方法综合分析问题，根据自己的基础知识和能力素养灵活选择恰当的方法解决问题。