数形结合助推理，分类讨论得高分

文／吴思佳

在一些问题的设计中，由于图形的形状（点、边）不确定，得到的结论可能不相同，这时，我们就要进行分类讨论。比如等腰三角形中底与腰的不确定，全等三角形、相似三角形的对应点不确定等。

（1）求反比例函数与一次函数的表达式；

（2）若点P为x轴上一点，△ABP是等腰三角形，求点P的坐标。

（2）由（1）知，AB=5。根据题意可分三种情况讨论：

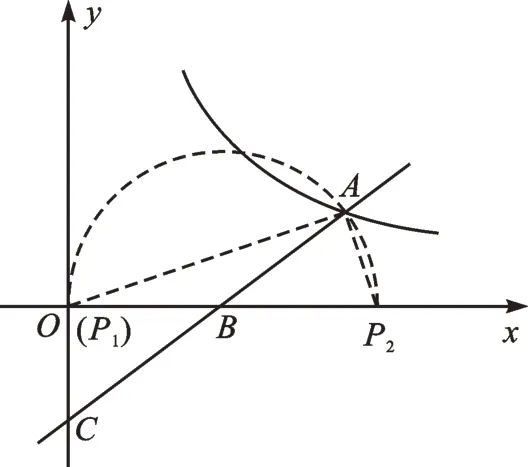
图1

①当AB=PB时，如图1，以点B为圆心、AB长为半径的圆与x轴的交点为点P1、P2。

∵△ABP是等腰三角形，∴PB=5。

∴P1（0，0）或P2（10，0）。

②当AB=AP时，如图2，以点A为圆心、AB长为半径的圆与x轴的交点为点P3。过点A作AD垂直x轴，由（1）知，BD=4，易知点P3与点B关于AD对称，∴DP3=BD=4。

∴OP3=5+4+4=13。∴P3（13，0）。

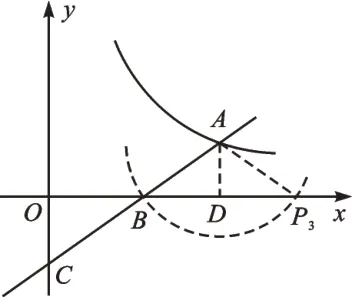
图2

【评析】由于条件“△ABP为等腰三角形”指代不明，导致点P的位置不确定，故要分AB=PB、AB=AP、PB=AP三种情况进行探究。由等腰三角形的性质与圆的对称性解出P1、P2和P3各得1 分，再利用勾股定理建立方程解出P4得2分。

例2 在平面直角坐标系中，已知抛物线L：y=ax2+（c-a）x+c经过点A（-3，0）和点B（0，-6），L关于原点O对称的抛物线为L′。

（1）求抛物线L的表达式；

（2）点P在抛物线L′上，且位于第一象限，过点P作PD⊥y轴，垂足为D。若△POD与△AOB相似，求符合条件的点P的坐标。

【解析】（1）由题意，得

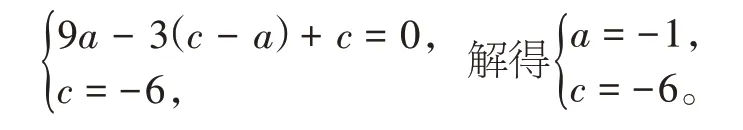
∴抛物线L：y=-x2-5x-6。

（2）∵点A（-3，0）、B（0，-6）在L′上的对应点分别为A′（3，0）、B′（0，6），∴设抛物线L′的表达式为y=x2+bx+6。将A′（3，0）代入y=x2+bx+6，得b=-5，∴抛物线L′的表达式为y=x2-5x+6。

∵A（-3，0），B（0，-6），∴AO=3，OB=6。

设P（m，m2-5m+6）（m＞0）。

∵PD⊥y轴，∴D（0，m2-5m+6）。

∴PD=m，OD=m2-5m+6。

∵Rt△POD与Rt△AOB相似，

∴有Rt△PDO∽Rt△AOB或Rt△ODP∽Rt△AOB两种情况。

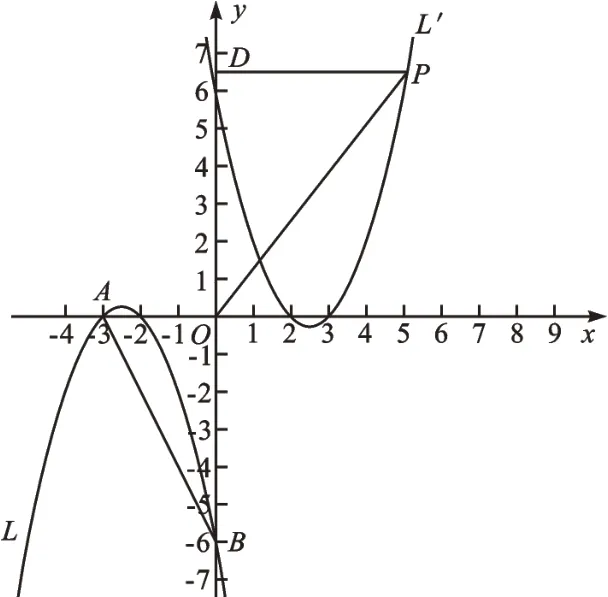
图4

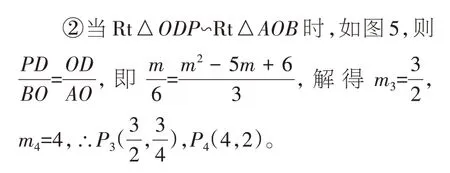
图5

【评析】第（1）小题，利用待定系数法解出抛物线L的表达式得2 分。第（2）小题，由中心对称特征求出L′的表达式得2 分，在△POD中，点O是定点，点P为抛物线上的主动点，点D为从动点，由图像确定相等的一组角，得出分Rt△PDO∽Rt△AOB或Rt△ODP∽Rt△AOB两种情况讨论得2 分，再利用相似三角形的性质分别求解点P，每个点各得1分。