坐标系中图形变换的解题策略和方法
文/张 丽
图形的变换主要包括轴对称、旋转、平移等几个方面。其中,对称常见的考查形式多以折叠为主,有时也会与特殊图形结合在一起出现;旋转的考查面比较广,常见的考查形式为与特殊三角形或特殊四边形结合出现在综合题中。
知识点一、轴对称
例1 如图1,在平面直角坐标系中,矩形OBCD的顶点O、B、C的坐标分别为(0,0)、(20,0)、(20,10),在线段OC、OB上各有一动点M、N,则当BM+MN取最小值时,点M的坐标是。

图1
【解析】由于BM+MN不在同一直线上,所以我们要想办法把它们转化到同一直线上。作点B关于OC的对称点B′,连接B′N,交OC于点M,如图2。这时,根据“两点之间线段最短”可以得到BM+MN的最小值为B′M+MN=B′N。
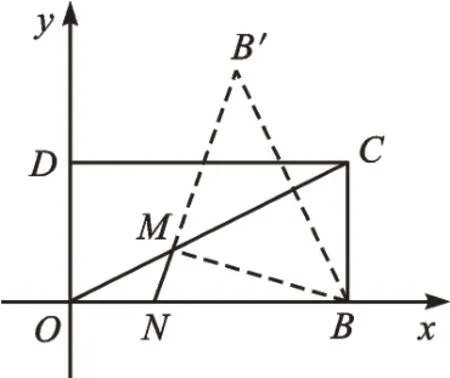
图2
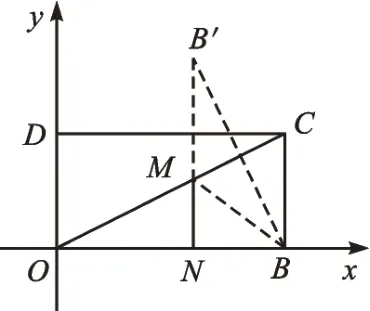
图3
因为N是x轴上的一个动点,B′是x轴外的一个定点,根据“直线外一点与直线上各点的连线中,垂线段最短”,可以得到当B′N⊥x轴时(如图3),BM+MN的值最小。根据条件,计算得BB′=8。又因为△BB′N与△COB相似,可得BN=8,所以得到ON=12,MN=6,点M的坐标是(12,6)。
【点评】本题属于动点背景下的轴对称变换问题。我们应注意折叠前后所对应的图形,抓住它们之间的不变关系及其性质来寻找相等的量。同时,本题还综合利用了“两点之间线段最短”“垂线段最短”等知识点来解决问题。
知识点二、旋转
例2 如图4,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(-2,5)的对应点A′的坐标是。
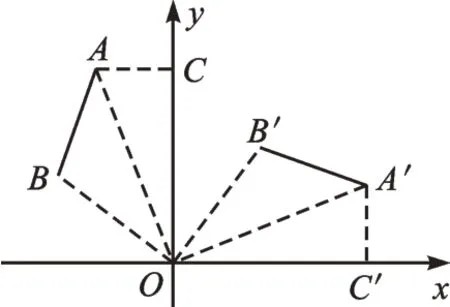
图4
【解析】∵线段AB绕点O顺时针旋转90°后得到线段A′B′,∴△ABO≌△A′B′O,∠AOA′=90°,AO=A′O。
作AC⊥y轴于点C,A′C′⊥x轴于点C′,如图4,则∠ACO=∠A′C′O=90°。
∵∠COC′=90°,∴∠AOC=∠A′OC′。
∴△ACO≌△A′C′O(AAS)。
∴AC=A′C′,CO=C′O。
∵A(-2,5),∴A′(5,2)。
【点评】本题考查了旋转的性质、全等三角形的判定及性质的运用、点的坐标的运用等知识,构造三角形全等是解决本题的关键。
变式 将含有30°角的直角三角板OAB放置在平面直角坐标系中,如图5,OB在x轴上,若OA=2,将三角板绕原点O顺时针旋转75°,则点A的对应点A′的坐标为。
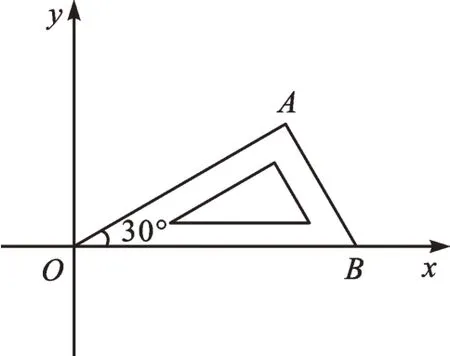
图5
【解析】如图6,过点A′作A′C⊥OB于点C。
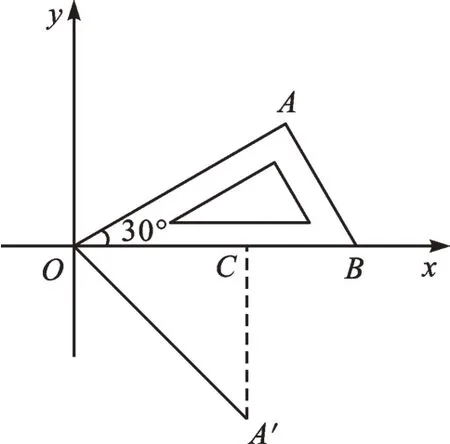
图6
∵将三角板绕原点O顺时针旋转75°,
∴∠COA′=45°,OA′=OA。
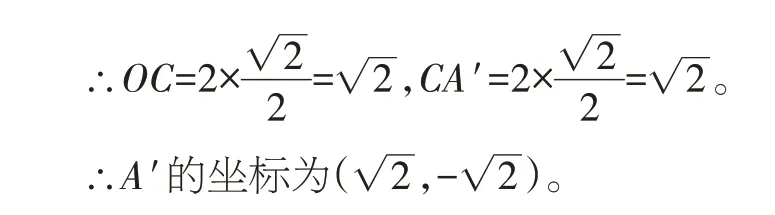
【点评】解题的关键是首先根据题意找到点A′的位置,然后依据旋转的定义和性质得到OA′的长和∠COA′的度数,再利用特殊锐角三角函数值求解。其中,∠COA′=45°是解题的重要突破口。
知识点三、平移
例3 如图7,已知A、B的坐标为(2,0)、(0,1),如果把线段AB平移至A1B1,那么a+b的值为()。
A.2B.3C.4D.5
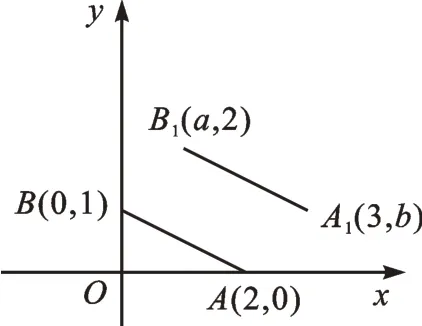
图7
【解析】根据点B平移后的纵坐标变化、点A平移后的横坐标变化,可以得到线段AB的平移规律:向上平移1 个单位,再向右平移1 个单位(或先向右移,再向上移)。由此,我们可以知道线段上每一个点均按此规律平移,可得a=0+1=1,b=0+1=1,所以a+b=2。故选A。
【点评】本题主要考查了坐标系中点、线段的平移规律:在平面直角坐标系中,整个图形的平移情况和图形中某一点的平移情况是相同的。平移中点的变化规律是:图像向右移动,点的横坐标则加;图像向左移动,点的横坐标则减。图像向上移动,点的纵坐标则加;图像向下移动,点的纵坐标则减。

