从“易”错题到“难”错题

文／陈建

“统计与概率”作为中考试卷中的常客，难度不大，是易于将全分“收入囊中”的一类问题。但如果同学们在解题时不认真审题，不深入思考，不细致考虑，错误往往就会在不经意间发生。下面，我们带领大家对一些常见的错误进行分析，希望能让你在不经意间出过的“错”不再重现。

一、理解不深刻，导致错误

例1 某体育用品专卖店在一段时间内销售了20双学生运动鞋，各种尺码运动鞋的销售量如下表。则这20双运动鞋的尺码组成的一组数据的众数是________。

__________________________________27___________________________________2尺码/cm____销售量/双___25__1____25.5__5____26__9____26.5______3_______

【错解】9。

【错因分析】本题主要考查如何求一组数据的众数，正确理解众数的概念是解题的关键。众数是指一组数据中出现次数最多的数，并不是指出现的次数。此题数据以表格的形式呈现，从表格中可以看出，26cm 的鞋共销售了9双，在20 个数据中26 共出现了9 次，次数最多，所以众数应为26，而不是9。

【正解】26。

【点评】在解决统计问题时经常会遇到题目中的数据以表格形式呈现，我们要能够正确提取表格中的相关信息，区分好数据以及每个数据出现的次数，正确理解众数的概念，不能把众数误解成数据出现的次数。

二、思考不全面，导致错误

例2 一组数据3、4、5、8、a的极差为7，则a的值为________。

【错解】10。

【错因分析】一组数据的最大值与最小值的差就是该组数据的极差。有些同学看到此题中的3、4、5、8是从小到大排序的，而a又放在了最后位置，因此形成思维定式，认为a就是最大值，然后根据a-3=7，得出a的值为10。

【正解】本题并没有说明数据是按大小关系排序的，因此a可能是最大数，也有可能是最小数，也有可能在3 和8之间。当a在3 和8 之间时，极差为5，不合题意；当a是最小数时，根据8-a=7，可以求得a的值为1；当a是最大数时，根据a-3=7，可以求得a的值为10。所以a的值为1或10。

【点评】求极差的关键是要能够正确找出数据中的最大值和最小值，如果题中有数据不确定，此时要更加全面地思考，分情况讨论不确定数据的大小。

三、审题不清晰，导致错误

例3 从2 名男生和2 名女生中任选2名学生参加志愿者服务，求选出的2名学生中至少有1名女生的概率。

【错因分析】任选2名学生参加志愿者服务，属于“不放回试验”，如果在列表或画树状图时看成是“放回试验”，就会产生错解。本题还要注意“至少有1名女生”是指“1名或者2名女生”都是符合题意的结果数。

【正解】解：根据题意，列表如下。

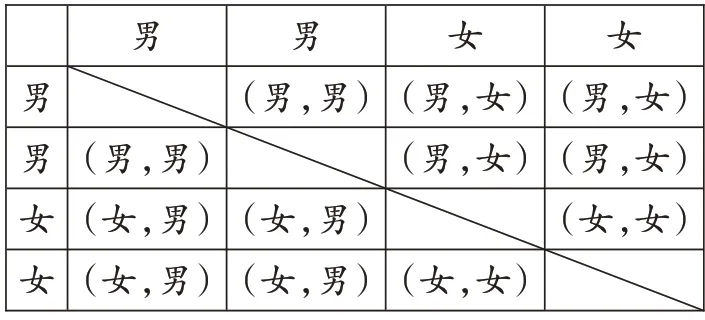
男男______女______女___男男女女（男，男）（男，男）（女，男）（女，男）（男，女）（男，女）（女，男）（女，男）（女，女）（男，女）（男，女）（女，女）

所以P（选出的2 名学生中至少有1名女生）=。

【点评】此题主要考查用列表法或画树状图法求概率，两种方法都适用于两步完成的事件，解题时要审清题意，明确事件属于放回试验还是不放回试验。同学们也可以尝试用画树状图的方法求解。

易错题往往不是不会做，而是由于概念不清、思考问题不全面、思维定式等多种因素的影响在不经意间失分。希望在今后的学习中，同学们能够多一份细心，少一份粗心，把“易”错题变成“难”错题。