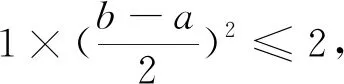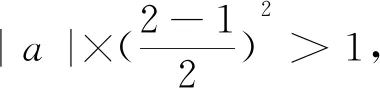二次函数极差的规律与应用

刘国华

江苏省海安市实验中学 (226600)

二次函数是重要的基本初等函数之一，备受命题者的青睐，许多高考题、调研试题均以二次函数为背景考查学生素养．其中双重最值问题综合性强，难度大，能力要求高，是学生眼中的难题．笔者从熟题入手，优化处理方法，揭示其变化规律，帮助学生提高解决此类问题的能力．

1.再现熟题，方法优化

为表述方便，将函数f(x)在闭区间[m,n]上的最大值与最小值的差称为函数f(x)在闭区间[m,n]上极差．

引例若二次函数f(x)=a(x-h)2+k(其中a≠0)，求函数f(x)在区间[x0-l,x0+l](其中l>0)上的极差．

解析:记区间[x0-l,x0+l]中点x0到对称轴x=h的距离为d，则d=|x0-h|≥0．

(1)若d>l，极差为|f(x0-l)-f(x0+l)|=

|2al(2x0-2h)|=4|a|l|x0-h|=4|a|ld．

(2)若d≤l．

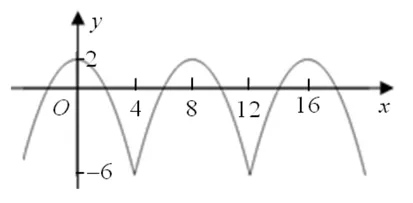
①当x0-l≤h

②当x0≤h≤x0+l，即d=h-x0时，极差为|f(x0-l)-f(h)|=|a(x0-l-h)2|=|a|[(h-x0)+l]2=|a|(d+l)2．

由①②可知，若d≤l，极差为|a|(d+l)2．

综合(1)(2)得：若d>l，极差为4|a|ld；若d≤l，极差为|a|(d+l)2．

2.反思结果，规律显现

揣摩上述结果，分析二次函数f(x)=a(x-h)2+k(其中a≠0)在区间[x0-l,x0+l](其中l>0)上的极差的影响因素，不难得出如下结论：

规律1 在区间[x0-l,x0+l](其中l>0)上，|a|越大极差越大．

规律2 在区间[x0-l,x0+l](其中l>0)上，l越大极差越大，即区间越长极差越大．

规律3 在区间[x0-l,x0+l](其中l>0)上，d越大极差越大，即区间中点到对称轴的距离越远极差越大．

由规律3易得规律4，当d=0，即二次函数的对称轴处于区间中点时，极差取到最小值|a|l2．

以上4点指明了二次函数在闭区间上最大值与最小值的差(即极差)的变化规律．从最近发展区出发，多思考一点，形成直达本质的认识，有利于提高学生解决问题的能力．

3.应用规律，难题突破

例1 (2017全国高中数学联赛一试A卷第9题)设k,m为实数，不等式|x2-kx-m|≤1对所有x∈[a,b]成立，则b-a的取值范围是．

例2 (2018年江苏省海安市高三期中调研)已知函数f(x)=ax2+bx+c(其中a,b,c为实数，且a≠0)，若对于任意b,c，存在x0∈[1,2]，使得

|f(x0)|>1，则实数a的取值范围是．

例3 (2018年南师大附中高三期中考试)已知实数a,b,c∈[0,4]，若a2,b2,c2是公差为2的等差数列，则|a-b|+|b-c|的最小值为．

取函数f(x)=x2，问题转化为：若0≤a

例4 (2018年金陵中学高三12月检测)已知偶函数y=f(x)满足f(x+4)=f(4-x)，当x∈

图1

解析:因为y=f(x)是偶函数，所以f(x+4)=f(4-x)=f(x-4)，即函数f(x)的周期为8，图像如图1所示．

|f(xi)-f(xi+1)|表示函数f(x)在区间[xi,xi+1]上的极差，由结论2知|f(xi)-f(xi+1)|≤8．又因为2018=8×252+2，所以要使n+xn的值最小，须x1=0，xi+1=xi+4(i=1,2,…,253)，所以n=254，x254=x253+2=252×4+2=1010，故n+xn的最小值为1264．