厘清概念 领悟意义
2021-11-23 08:29文/周洁
初中生世界 2021年43期
文/周 洁
极差、方差反映了一组数据的稳定情况,是初中数学统计知识的重要内容,广泛应用于生活中。下面请同学们跟随老师一起来感受这两个知识点。
一、极差
例1 若一组数据为1,-2,3,2,则这组数据的极差为________。
【解析】根据极差的概念,得这组数据的极差=3-(-2)=5。
【点评】本题考查极差的概念,极差=最大值-最小值。
变式 若一组数据3,4,5,x的极差是5,则x=________。
【解析】当x是最小的数时,5是最大的数,5-x=5,解得x=0;当x是最大的数时,3是最小的数,x-3=5,解得x=8,所以x的值为0或8。
【点评】当不确定一组数据的最大值和最小值时,需要分类讨论。
二、方差

【解析】由图像可知乙的数据波动较大,偏离平均数较大,故方差大。
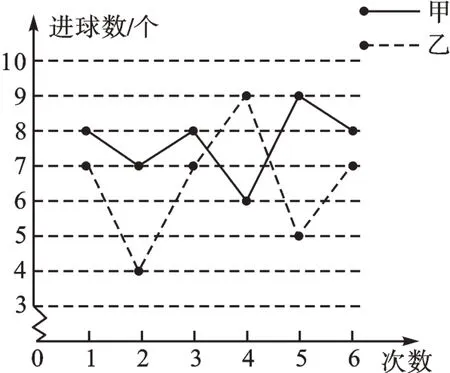
图1

变式2 例2 中若小华再射击1 次,命中8 环,则6 次成绩的方差________。(填“变大”“变小”或“不变”)

【点评】一组数据增加一个这组数据的平均数后,平均数不变,但总数量增加了1,因此,利用方差公式可知方差变小。

【解析】从公式中可知共有8 个数据,平均数为4,要求x1+x2+…+xn,即求出这8 个数据的总和,所以可得答案为8×4=32。

猜你喜欢
中学生数理化(高中版.高考数学)(2021年3期)2021-06-09
新丝路(下旬)(2018年7期)2018-05-14
小天使·五年级语数英综合(2017年11期)2017-11-30
初中生世界·九年级(2017年10期)2017-11-08
中学生数理化·八年级数学人教版(2016年5期)2016-08-23
中学生数理化·八年级数学人教版(2016年5期)2016-08-23
中学生数理化·八年级数学人教版(2016年5期)2016-08-23
中学生数理化·八年级数学人教版(2016年5期)2016-08-23
中学生数理化·八年级数学人教版(2016年5期)2016-08-23
东方女性(2016年4期)2016-04-28

