紧扣本质 巧算方差

文／张伟俊

方差是刻画一组数据离散程度的统计量，它是一组数据中的每一个数据与其平均数的差的平方的平均数。一组数据的方差越大，它的离散程度就越大（波动越大）；一组数据的方差越小，它的离散程度就越小（波动越小）。但是，在应用方差公式解决问题的时候，有些同学总是觉得这个公式记忆起来、计算起来都很难，容易产生错误。因此，我们有必要进一步来理解方差概念的本质，探索方差计算的简便方法，从而提高解决问题的正确率。

一、理解公式，灵活应用

上述两种计算方差的公式在实际操作中各有各的优势。“先平方再作差”，虽然操作简洁，但参与运算的数值往往较大；“先作差再平方”，虽然操作繁琐，但相对来说参与运算的数值会小一些。因此，在实际应用中，我们可以视情况灵活应用这两种公式来计算方差。

例1 计算数据1，2，3，4，5的方差。

比较上述两种方法，可以发现：一般情况下，计算方差还是运用方法1 比较简便，而当计算各个数据与平均数的差的平方比较麻烦，且直接计算各个数据的平方比较简单时，运用方法2比较简便。

二、数形结合，直观判断

数和形是数学研究的两个主要对象，它们各有特点，也各有各的优势。在解决问题的时候，我们经常运用数形结合、数形转化的方法，或以数辅形，或以形助数，优化解决问题的思路和方法。比较几组数据的离散程度，就是比较这几组数据方差的大小，这可以通过计算方差来比较，但有时候也可以从形的角度来判断。

例2 （2020·辽宁盘锦）在市运动会射击比赛选拔赛中，某校射击队甲、乙、丙、丁四名队员的10 次射击成绩如图所示。他们的平均成绩均是9.0 环，若选一名射击成绩稳定的队员参加比赛，最合适的人选是 。

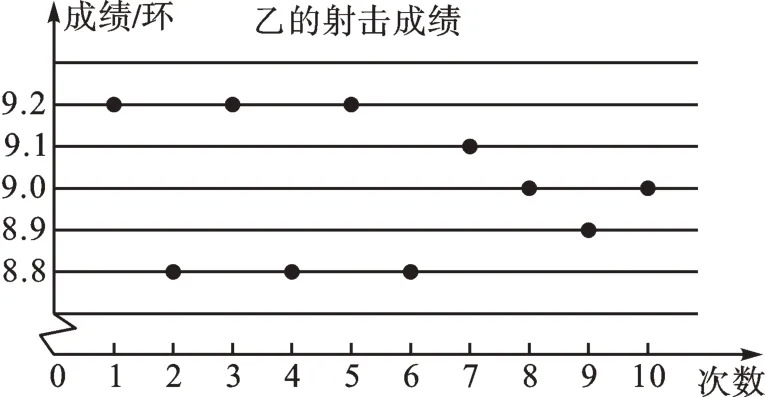
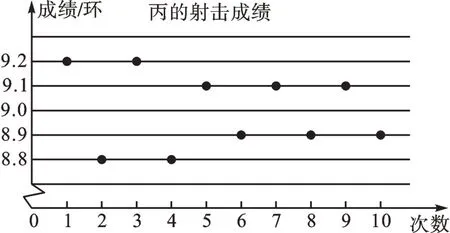
【解析】四名队员的平均射击成绩相同，要从中选择一名射击成绩稳定的队员参加比赛，就是要选出射击成绩方差最小的队员参加比赛。

方法2：从本质上讲，方差反映的是一组数据偏离平均数的程度。从四名队员射击成绩的“散点图”可以直观地看出他们的射击成绩都在平均成绩9.0 环附近波动，乙、丙的波动幅度明显大于甲、丁的波动幅度。同时，甲、丁的前八次射击成绩都是4 个9.1 环和4 个8.9 环，而最后两次成绩甲是9.1 环和8.9 环，丁是两个9.0 环，因此，丁的波动幅度小于甲的波动幅度，即丁的成绩波动最小（最稳定），故选丁参加比赛。

比较以上两种方法，可以看出：方法1是从“数”的角度，通过计算作出准确判断，但是过程显得繁琐；方法2是从“形”的角度进行比较，显得直观、简洁。但是，我们要明白，当数据排列复杂时，从“形”的角度往往很难作出准确判断，所以从“形”的角度进行比较是有局限性的。因此，我们在实际应用中，还是要具体情况具体分析，数形结合，选择适切的方法。

三、把握规律，化繁为简

在数学学习的过程中，同学们常常会发现一些重要的结论或规律，并运用这些结论或规律解决问题。因此，从某种程度上讲，数学学习也是一个发现规律、把握规律并运用规律的过程。在方差的学习过程中，你有哪些发现呢？

例3 （2019·浙江杭州）称量五筐水果的质量，若每筐以50 千克为基准，超过基准部分的千克数记为正数，不足基准部分的千克数记为负数，甲组为实际称量读数，乙组为记录数据，并把所得数据整理成如下统计表（单位：千克）。

实际称量读数和记录数据统计表

通过以上探究，我们可以发现一个重要结论：如果数据x1，x2，x3，…，xn的平均数和方差分别为-x、s2，那么数据x1+a，x2+a，x3+a，…，xn+a的平均数和方差分别为-x+a、s2。其实道理很简单，每个数据都增加了a，平均数当然也增加了a；每个数据都增加了a，说明这组数据的波动幅度没有变化，所以方差保持不变。运用这个结论，我们就可以简化一些数值较大的求平均数和方差的问题。比如：求数据1001，1002，1003，1004，1005 的平均数和方差，就可以先求数据1，2，3，4，5的平均数和方差。

除此以外，平均数和方差还有一些重要的性质（如下表）值得我们去探究，请同学们自己动手去推导一下吧。

___________________________________序号_______x1，x2，x3，…，xn x1+a，x2+a，x3+a，…，xn+a_____kx1，kx2，kx3，____________…，kxn kx1+a，kx2+a，kx3+a，…，kxn+a__平均数_-x_____-x+a k-x____k-x+a___方差s2 s2 k2s2__k2s2