指向学生思维进阶的小学数学习题设计策略*

杨宏伟 赵国防

苏联教育家斯托利亚尔说：“数学教学说到底是数学思维的教学。”南京大学郑毓信教授指出：数学教学必须超越具体知识和技能，深入到思维的层面，由具体的数学方法和策略过渡到一般性的思维策略与学生思维品质的提升，帮助学生通过数学学会思维，提升思维的综合性与灵活性、自觉性与创造性、严谨性与深刻性等。作为训练学生思维的重要载体，习题的价值不言而喻。在数学教学中，教师应注意巧妙设计习题，使其更好地体现知识的本质，促进学生在问题解决过程中更好地培养思维的灵活性、系统性、深刻性，实现思维进阶。

一、从“一题”到“多题”：在巧妙变化中培养学生思维的灵活性

灵活多变不仅仅是对习题的基本要求，也是训练学生思维的一种重要方式。教材中呈现的例题与习题由于侧重知识的应用与实践，常常比较简约。在教学中，教师可以在尊重教材原创的基础上，融入个人的思考与理解，创造性地将“一题”转化为“多题”，引导学生站在联系的角度感受知识的整体性与连贯性，挖掘其隐性的知识结构，培养学生的观察、比较、分析等数学学习能力，提升他们思维的聚力点，培养他们思维的灵活性，促进其思维向纵深发展。

如教学苏教版六上“长方体和正方体的表面积”时，有这样一道习题：一个棱长6 厘米的正方体，它的表面积是多少平方厘米？教师引导学生解答并评析后，依据知识特点和学情依次呈现下面两个问题：（1）把一个棱长6 厘米的正方体平均分成两个一样的长方体，（如图1）这两个长方体的表面积之和比原来增加了多少平方厘米？借助图例，让学生初步感知：这两个长方体的表面积之和比原来增加了正方体2 个面的面积，初步建立知识表象，理清基本概念。（2）把一个正方体平均分成两个一样的长方体，其中一个长方体的表面积是144 平方厘米，原来正方体的表面积是多少平方厘米？基于概念，用已有知识进行解答，引导学生从不同角度加以分析、思考，再次聚焦“分成的两个长方体的表面积之和比原来的正方体多出其2 个面的面积”这一基本概念，促进他们感受数学学习的整体性。教师收到作业1（如图2）和作业2（如图3）。毫无疑问，两种解题方法都合情合理。苏联教育家乌申斯基强调：比较是一切思维和理解的基础，我们正是通过比较来了解世界上的一切的。学生比较后会发现：作业1 注重知识的生长点，依托原有经验进行常规性的解答，其中一个长方体的表面积其实就是原来正方体4个面的面积之和；作业2注重知识的延伸点，另辟思维路径，充分、巧妙地转化关键点。

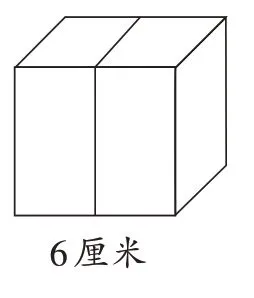
（图1）

（图2）

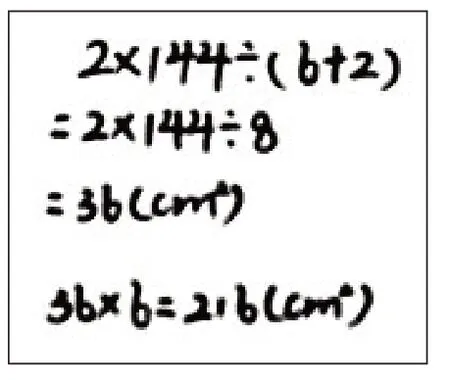
（图3）

教师巧妙地一题多用，不断挑战与刷新学生的原有认知。一方面，通过“这两个长方体的表面积之和比原来增加了多少平方厘米？”纵向比较，促进学生整体理解这两个长方体的表面积之和比原来增加的其实就是原来正方体2 个面的面积，积累初步的活动经验，感知概念的表象；另一方面，通过“其中一个长方体的表面积是144 平方厘米，求原来正方体的表面积”横向比较，促进学生全方位运用概念，体会到两个长方体的表面积之和其实就是原来正方体的表面积加上新增的2个面的面积，即正方体8个面的面积之和。促进学生在辨析、思考、对话、交流的过程中，不断碰撞出思维的火花，产生新思路、新方法，逐步形成对数学概念的全方位理解。围绕“一题”设计“多题”，充分打开了学生的思维，在一定程度上培养他们思维的灵活性。

二、从“新题”到“旧题”：在新旧关联中培养学生思维的系统性

深度学习的一个重要特征就是系统化思维，训练系统化思维也是促进儿童思维发展的一条重要路径。在习题设计中，教师要巧妙而及时地链接之前的学习，从知识系统化的角度出发，实现从“新题”到“旧题”的理性回归，引导学生更加精确、综合、深入地认识和理解数学，为培养其思维的系统性提供来自知识本身的结构化支撑。

（图4）

例如，苏教版五下“圆”单元的“整理与练习”中有如图4 所示的一道思考题，要求学生综合运用本单元所学的知识解决问题。《义务教育数学课程标准（2022 年版）》（以下简称“新课标”）强调：在小学阶段要加强字母式运算，加强代数推理。因此，在解决问题的过程中，教师引导学生借助字母r来表示圆的半径，先求出r2，再计算圆的面积，（如图5）整个分析过程看似平淡无奇，却动态呈现了知识的本质，促使学生初步尝试用字母表示来解决问题，渗透了转化等数学思想方法，有效推动学生从知识的表层走向知识的内涵，促进了他们的思维进阶。然而，对于“用字母表示”这一解决问题的方法，学生很多都只是瞬时记忆，后续难以真正“用起来”。基于真实学情，教师需要找到更有效、更直接的方法，既能推动学生串联知识，促进数学方法的迁移，又能使得数学知识与学生思维训练之间有效联结。“圆”单元就有如图6 所示的这样一道例题。

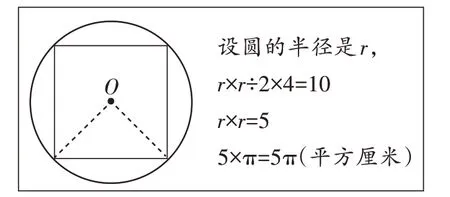
（图5）

（图6）

在实际教学中，教师要注意引导学生通过操作及问题间的比较，初步感知圆的面积是它半径平方的3 倍多一些，即圆面积是正方形面积的π倍。这一题设是基于学生循序渐进的思考过程而形成的，但这仅仅局限于题设表面，我们需要掌握知识的本质，由“表”及“里”，有结构地呈现此类问题的基本数学模型，引导学生深刻理解分析与解决此类问题的方法。

郑毓信教授强调，数学教学不应“求全”，而要“求联”。在上述例题中，当小正方形的边长等于圆的半径，圆面积是正方形面积的π倍，由这一表象关联到一类问题，就能换一种思路来解答了。新课标强调：要让学生积累数学活动经验，形成模型意识，构建普适的数学模型，分析和解决问题。这样学生很快就能发现，可以先求小正方形的面积，再根据数学模型求出圆的面积是5π。（如图7）

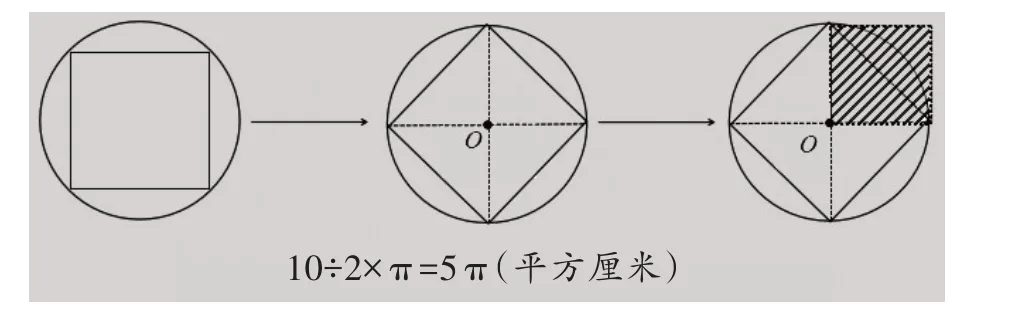
（图7）

借助习题，巧妙链接之前的例题，这时新旧知识完全打通，学生的思维得到了有效迁移，培养了他们思维的系统性。基于以上思考，笔者设计了两道新题，以例题为基础引导学生进行深度研究，探究知识的本源，建立适配的数学模型，旨在推动学生深刻体会和感悟数学，提高其分析与解决问题的能力。

（1）三角形的面积是5，圆的面积是多少？（如图8）

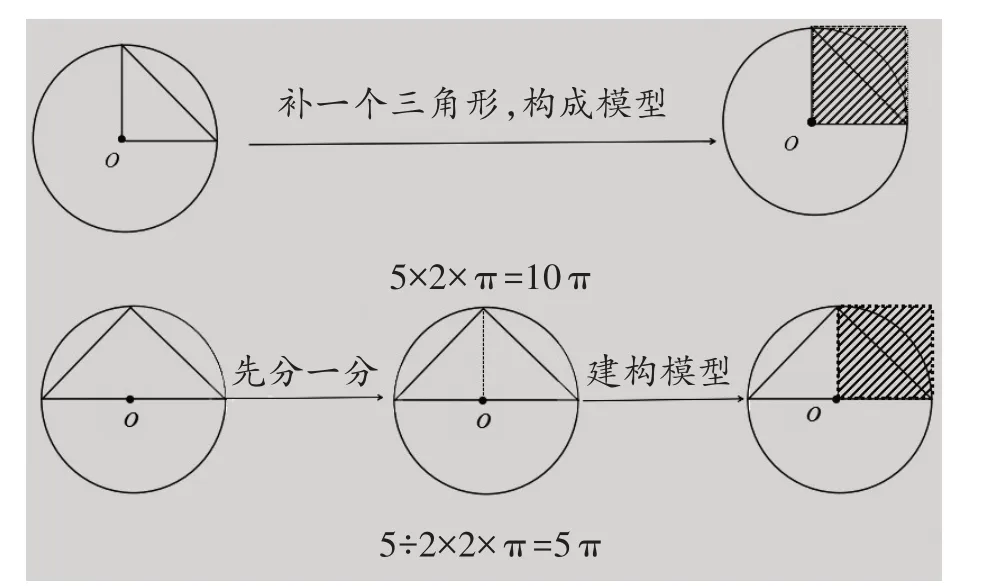
（图8）

（2）圆的面积是62.8，阴影部分的面积是多少？（如下页图9）

上述教学中，借助一道例题巧妙连接旧题，并精心设计新题，彻底实现了由“新”到“旧”、由“旧”到“新”的思维体系。同时，以习题的呈现为明线，以思维的进阶为暗线，明暗交织，共同指引学生的思维路径走向“连续”，从而促进学生从多个角度建构清晰、完整的数学模型，形成有序的思考路径，为其系统性思维的发展提供了拓展支撑。总之，通过“新”“旧”系统化的链接，在关联与创新中切实培养了学生思维的系统性。

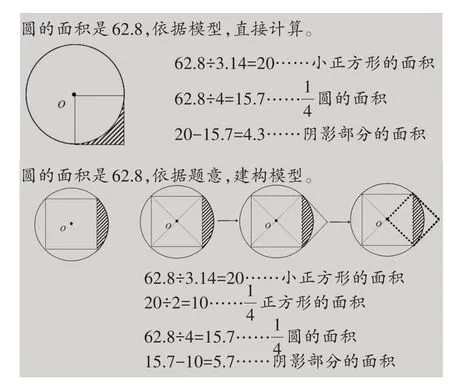
（图9）

三、从“单题”到“题组”：在对比理解中培养学生思维的深刻性

学生学习数学的过程其实是一种深刻理解的过程。为了促进学生形成清晰的认知，教师教学时要注意借助必要、及时的对比，切实培养其思维的深刻性。我们要以课堂为载体，借“题”变“题”，延展习题外延，促进学生理解习题内涵，凸显其思维能力的培养。同时，要通过巧妙的习题训练，引导学生从“理解”走向“深思”，从“对比”走向“深刻”，明晰探究思路，优化思维进阶路径，推动其思维轻松进阶。苏教版六上“分数除法”单元呈现了如图10 所示的一道例题，注重基础知识的生成，反映关键推导能力层面的设计。基于习题外延以及指向不同核心素养要素的目标的有机整合，笔者进行了借“题”变“题”。

（1）在下图中分一分，表示出结果。

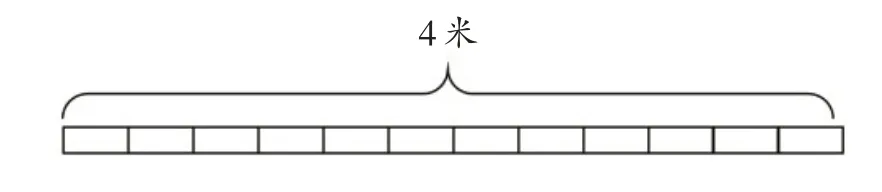
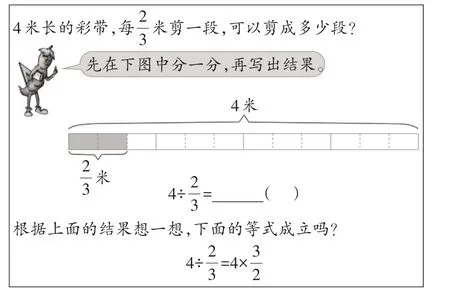
（图10）

这样做，主要体现了以下三点思考：

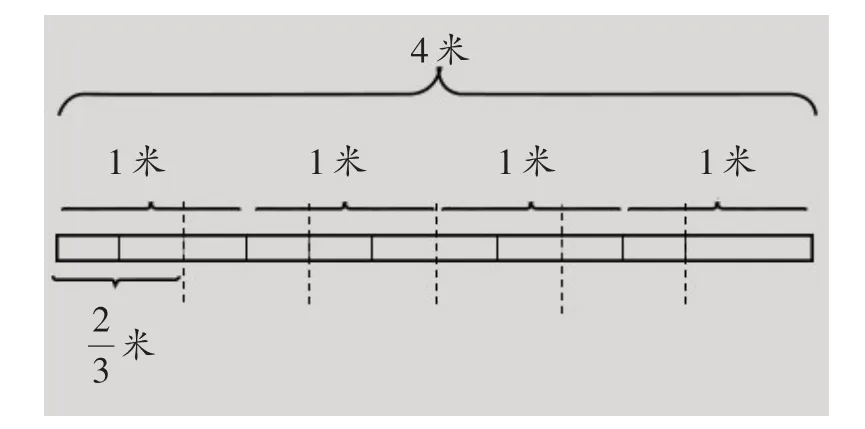
一是夯实基础，激活思维。上题中的题（1）让学生在新的学习场域中理解数学知识，实则是理解数学。在课堂教学中，不少教师会采用数形结合的方式引导学生初步理解整数除以分数的方法，但学生往往只是机械记忆整数除以分数的计算方法，而忽略计算方法的形成过程。基于此，上述题（1）从指向知识表面走向深度解析，精准把握“切入点”，助力学生顺利实现深度理解。解题时，首先要请学生理解米的含义，根据图意，选择1 米的作为切入点，细化单位，画出示意图（如图11）；然后引导学生理解“图”与“算”相结合，用“图”验证“算”，注重知识的形成过程，促进他们理解知识本质。

（图11）

二是引发探究，延展思维。题（2）需厘清探究思路，深入知识本质，聚焦每一个环节所指向的问题。题（2）中的第一问要求学生结合图意进一步理解算理，构建新的学习主体环节。图中的4 米可以分成4 个1 米，其中的每一小段表示1米的，即米，1米里有3小段，4米里就有4×3=12（段），所以4×3 表示4 米里面包含12 个米。第二问凸显“会想”，要求学生明晰思维路径，多角度探究其本质。中的表示什么呢？不妨换一个角度来思考，每段表示米，即每米可以剪成段，这样4 米就可以剪成=6（段）。基于学科本质，通过相互关联的两道题，聚焦知识外延，关注问题驱动下的深度理解，指导学生开展真实有效的问题探究，搭建学习“支架”——数形结合，促进其顺利实现“会算”和“明理”的双重发展。

三是问题解决，思维进阶。题（3）深入挖掘教材，注重追溯知识的本质内核，把学生的视域从“知识点”拓展到“系统网”。在此过程中，新旧知识不断碰撞、验证、运用与重构，引发学生的思维在对比理解中不断走向深刻。利用商不变的规律来说明，此题的重点在于验证，并追溯商不变的规律。一方面实现“会用”，聚焦一个知识点或核心概念来解决说明新问题，使学生经历知识发生、发展的完整过程，通过关联新旧知识，使他们初步体会知识的一致性，实现知识进阶；另一方面强调“活用”，在理清知识脉络的同时，内化学生的认知与探究，多角度引发他们深度思考，使其形成清晰、稳定、可迁移的学科知识框架，促进其素养提升。

综上所述，教师在进行习题设计时，要注意指向学生的思维进阶，要在尊重教材完整体系的基础上融入个人思考，实现创造性改编、创新性设计，从而引发学生深度思维，促进其核心素养全面提升。