通过数形结合感悟运算一致性*——以六上“分数乘分数”教学为例

陈国强

《义务教育数学课程标准（2022 年版）》强调，要让学生“感悟数的运算及运算之间的关系，体会数运算本质上的一致性，形成运算能力和推理意识”。教学苏教版六上“分数乘分数”时，通过打通整数、小数、分数运算之间的“阻断层”，借助数形结合思想方法联系好“关联带”，从计数单位的核心概念角度重建“承重墙”，基于合情推理与演绎推理的展开，让学生完整地经历感悟整数、小数、分数运算一致性的过程，有助于他们提升运算能力，发展推理意识，习得素养品格。

一、课前思考

综观当下的“分数乘分数”教学，要在课堂教学中实现数运算的一致性，彻底打通整数乘整数、小数乘小数、分数乘分数的内在联系，实现新旧知识的整体性迁移内化，主要需要解决以下问题：

一是对算法处理的“浅表化”，不少教师过于强调“分子相乘的积作分子，分母相乘的积作分母”的算法，没有深入引导学生理解分子相乘的积表示计数单位的个数，分母相乘的积表示新的计数单位。

二是对算理解读的“偏差性”，如在“分数乘法”单元前两课时的学习中，分数乘整数、整数乘分数在运算过程中没有产生新的计算单位，而教师对分数乘分数产生新的计数单位后再累加计算单位甚少提及，容易导致学生在算理理解上出现偏差。

三是对算律运用的“缺失感”，一些教师注重借助数形结合推理算理和算法的合理性，但缺少对分数乘分数结果的演绎推理过程，适时介入分数与除法的关系以及运算律的运用，能促进学生高阶思维能力的提升。

二、课例实践

为了帮助学生精准理解和建构“分数乘分数”算理、算法的一致性，笔者重组教材内容，聚焦矩形面积，以数形结合、逻辑推理为主要表征方式展开教学。

（一）借助面积模型，初步探究算理

1.问题呈现，独立探究

师：要求这个长方形的面积，应如何列式？

2.交流分享，融理于法

师：下面，请小组派代表上台汇报。

生2：我们利用信封提示，根据分数与除法的关系将算式转化成（1÷2）×（1÷4）=1×1÷2÷4=（1×1）÷（2×4）=1÷8=。

生3：我们小组将一张纸上下对折，然后左右对折两次得到这张纸的。

生4：我们小组与折纸的方法类似，是用画线段图的方法来表示的，把一条线段看作单位“1”，先平均分成2 份，取出其中的1 份，然后在中再平均分成4 份，取出其中的1 份，就得到这条线段的。

生5：我们组也是采用画图的方法来验证的，只不过画的是长方形，我们将这个长方形看作单位“1”，一共平均分成了8份，其中的1份就是。

（二）数形结合分析，明晰算理算法

1.再次验证，归纳算法

师：你们也是用这种方法吗？为什么不用分数转化成小数或者折纸等其他方法呢？

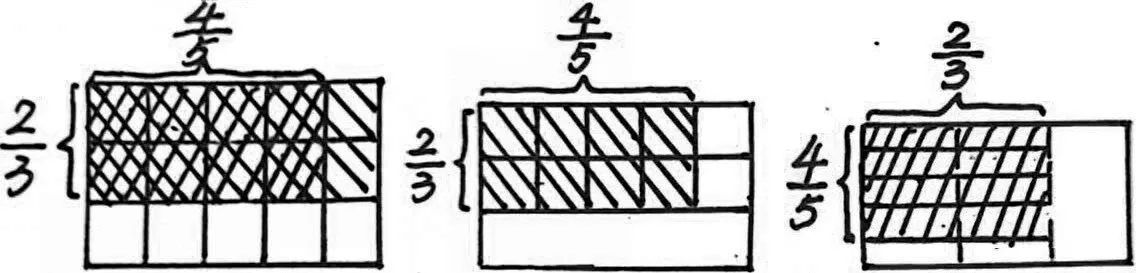
师：老师这里还有两幅作品，我们不妨把三幅作品（如图1）放一起对比一下。画得都对吗？你更欣赏哪一幅？

（图1）

生3：其实三幅作品都对，但我更喜欢第一幅作品，它能让我们一眼就看出把单位“1”平均分成15份，取这样的8份，也就是的是。

师：这里的15 份是怎么看出来的？8 又是怎么看出来的？

生3：因为长被分成5 列，宽被分成3 行，所以5×3=15（份），而涂色部分长为4，宽为2，4×2＝8（份）。

生4：老师，其实就是分子相乘的积作分子，分母相乘的积作分母。

师：非常棒！你们都发现了吗？这就是分数乘分数的计算方法，这里分母相乘得到的积就相当于单位“1”均分的总份数，而分子相乘的积就是取的份数。

2.数形结合，理解算理

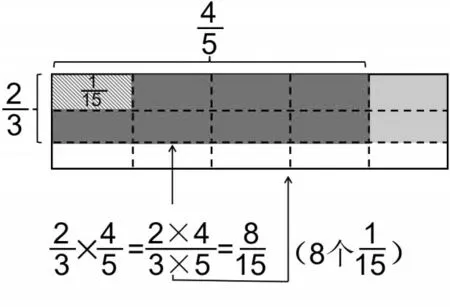
师（出示图2）：让我们聚焦这个长方形，分母相乘求得一共的份数，分子相乘求得取的份数，结果是，请问，它的计数单位是什么？你知道怎么来的吗？

（图2）

（三）横向对比反思，建立统一结构

1.对比呈现，内化结构

出示图3，带领学生进行回顾。

（图3）

师：我们刚才对分数乘分数进行分数单位的拆分与相乘，其实，在以前学习的整数乘法、小数乘法中也可以进行拆分与相乘，仔细观察，你有什么发现？小组交流后汇报。

生1：我们组发现这三组算式都有10、0.1、几分之一这些计数单位。

生2：我有补充，我发现它们的结果都跟两个乘数的计数单位和计数单位的个数有关。

师：是啊，无论是整数乘法、小数乘法还是分数乘法，本质上都是把两个乘数的计数单位的个数相乘，得到新的计数单位的个数；把两个乘数的计数单位相乘，得到新的计数单位，最后求出它们的积是多少。

2.练习巩固，深化理解

交流汇报，教师点评。

本节课以“计数单位”为核心概念，以“计数单位与计数单位相乘，计数单位上的数字与计数单位上的数字相乘”为基本运算，以“运算律”“等式的基本性质”为基本规律，经过三次探索，借助数形结合，对矩形的长和宽进行“先分后取，再分再取”，帮助学生理解新的分数单位的数学本质，感悟整数、小数、分数乘法运算的一致性，促进他们不仅知其然，而且知其所以然。

三、实施建议

东北师范大学马云鹏教授指出：“教学数与数的运算一致性目的在于体现学习内容之间的内在关联，从关联中体会其中的核心概念，让学生更好地理解一个学科的基本原理。”对小学生而言，“一致性”即探寻数学学科本真，构建完整的知识结构。教师应抓住计算教学的核心要义，优化教学环节，促进新知建构。

（一）立足数形结合，深化结构理解

美国加州大学伯克利分校伍鸿熙教授主张，用“矩形面积”定义“分数乘分数”的含义。苏教版教材虽然借用了“矩形”，但少了“面积”的强化，教材中直观图呈现的算法清晰，但其算理却有种“雾里看花”的感觉。人教版与北师大版教材则都借助了“矩形面积”，先规定矩形面积为单位“1”，纵向将边长平均分成n份，得到第一个因数“a个”，横向将边长平均分成m份，得到第二个因数“b个”，然后由“a个分数单位个分数单位”得到“a×b个新的分数单位”，回归到“计数单位的累加”，实现整数、小数和分数乘法运算的一致性。因此，在本课中借助数形结合思想中的“以数解形”“以形助数”是实现运算一致性的基本路径，“相同计数单位累加”的核心概念能有效强化学生对数与运算本质的理解，从而促进他们建立起具有一致性、整体性、互通性的数的运算整体结构。

（二）感悟转化思想，培养推理意识

鼓励学生“像数学家一样思考”，需要在日常教学实践中渗透数学思想方法模型，本节课基于逻辑推理推演“分数乘分数”的算理、算法，主要涵盖两个方面：一是证明“分数单位”相乘与“非分数单位”相乘，本质上都是转化成“计数单位与计数单位相乘产生新的计数单位”后的累加；二是通过分数与除法的关系、运算律演绎推理出“分数乘分数”的结果是“分子相乘的积作分子，分母相乘的积作分母”。因此，通过分数与除法的关系以及运算律等核心知识的探究，有利于学生实现从直观想象到抽象推理的顺利过渡，促进学生“像数学家一样推理”，帮助其学会用整体、关联和发展的眼光看待数学问题，从而形成科学、理性的数学思维。

在数学教学中，我们应该站在更高的角度，基于教材编排意图以及学生认知现状，把“分数乘分数”放到更广阔的知识结构体系中，引导学生完整地经历感悟运算一致性的过程，促进他们深刻感悟数与运算的一致性，从而提升运算能力，发展推理意识，习得素养品格。