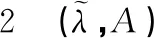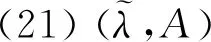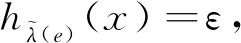犹豫模糊软超BCK代数

姜 曼,张 丹

(西安交通工程学院公共课部,陕西 西安 710300)

0 引 言

处理不确定性是经济学、工程学、环境科学、医学和社会科学等许多领域的一个主要问题,由于经典方法固有的缺陷,因此无法处理这些问题.为了克服这些困难,Molodtsov[1]提出了一种新的方法,称为软集理论,用于建立模型中的不确定性.在文献[2]中,Jun将软集的概念应用于BCK/BCI-代数的理论;Jun等[3]研究了基于软集理论的BCK/BCI-代数的理想理论;Maji等[4]将软集的研究扩展到模糊软集,引入了模糊软集的概念,并提出了模糊软集在决策问题中的应用;Babitha等[5]引入了犹豫模糊软集的概念,该概念结合了软集和Torra[6]的犹豫模糊集的优点;Jun等[7]将模糊软集应用于BCK/BCI-代数.超结构理论诞生于1934年,Marty给出了超群的定义,通过分析它的性质,将超群应用于群和关系代数函数.超代数结构是经典代数结构的自然扩展,在经典代数结构中,两个元素的组合是一个元素,而在超代数结构中,两个元素的组合是一个集合.目前,超结构在数学中有很多应用[8-11],特别地,Jun等[12]将超结构应用于BCK-代数,并引入了超BCK-代数的概念,它是BCK-代数的推广.关于超BCK代数的研究,文献[13-15]分别研究了超BCK-代数中的双极模糊关联超BCK-理想、双框架软集理论在超BCK-代数中的应用,以及超BCK-代数的模糊超BCK-蕴涵理想.本文我们引入了犹豫模糊软超BCK-理想、犹豫模糊软弱超BCK-理想、犹豫模糊软s-弱超BCK-理想和犹豫模糊软强超BCK-理想的概念,并研究其性质及相互关系,相关结论丰富和拓展了犹豫模糊软集和超BCK-代数理论.

1 预备知识

(H4)x<

在超BCK代数H中,对∀x,y,z∈H,且A、B和C均为H上的非空集合,则有:

(3) 0<

(4)A⊆B⟹A<

(6)A<<{0}⟹A={0};

定义2[12]设A是超BCK代数H上的一个非空子集,如果A满足以下条件:

(8) 0∈A;

则称A是H上的超BCK理想.

如果A满足(8)和

则称A是H上的弱超BCK理想.

定义3[15]设A是超BCK-代数上的一个非空子集,如果A满足(8)和

则称A是H上的强超BCK理想.

定义4[16]设U是一个集合,P(U)是U的幂集,E是一个参数集,A⊆E且F:A→P(U)是一个映射,称二元组(F,A)为U上的一个软集.

定义5[4]设U是一个集合,F(U)是U上的模糊集,E是一个参数集,A⊆E且F:A→F(U)是一个映射,则称二元组(F,A)为U上的一个模糊软集.

注1[4]由定义5可得,对∀e∈A,若F[e]为U上的一个模糊集,则称之为参数e的模糊值集.

定义6[6]设X是一个非空经典集合,一个X上的犹豫模糊集A的定义如下:

其中hA(x)是由区间[0,1]上若干个不同值构成的集合,表示X中的元素x属于集合A的若干种可能隶属度.记X上的全体犹豫模糊集为HF(X).

2 犹豫模糊软超BCK理想

本节若无其它说明,用H代表一个超BCK代数,用E代表一个参数集.

表1 二元运算的表示法

表的表示法

则有

即(16)成立.证毕.

引理1[17]令A是超BCK代数H的一个子集,如果I是H上的超BCK理想且满足A<

因此x∈Uε,所以Uε是H的超BCK理想.

反之,假设对∀ε∈[0,1],Uε≠∅是H的超BCK理想.

证明与定理1的证明类似,故略.

由(13)可得

证毕.

表的表示法

下面例子说明,H上的犹豫模糊软超BCK理想(犹豫模糊软弱超BCK理想)并不是H上的犹豫模糊软强超BCK理想.

由(19)可得

因此,x∈Uε,所以Uε是H上的强超BCK理想.

接下来,我们给出犹豫模糊软集成为犹豫模糊软强超BCK理想的条件.

由于Uk是H的强超BCK理想,则有x∈Uk,因此

定理7假设H满足条件:

由于Uε是H上的强超BCK理想,则有x∈Uε,因此有