并联五连杆点足式双足机器人稳定行走控制方法

孙双园,宋文杰,刘洧铖,钱义肇,付梦印

（北京理工大学自动化学院,北京 100081）

0 引言

双足机器人作为一种典型的地面移动平台,具有与人类相似的运动结构,能够代替人类完成危险任务,其研究近年来受到越来越多学者的关注。双足机器人最早的研究可追溯到20世纪80年代,日本早稻田大学开发了WABOT 系列机器人[1]。在此之后,日本本田公司开发的ASIMO 机器人[2-3]以及Trade and Industry 公司的HRP[4-5]系列机器人将双足机器人推向更加轻量化、人形化阶段。当前,最为知名和出色的双足机器人当属波士顿动力公司（Boston Dynamics）的Atlas[6]和Agility Robotics 公司的Cassie[7],前者出色的运动能力使其能够执行复杂动作,如后空翻和跑酷;后者则是一款用于服务的商用机器人,拥有出色的行走稳定性[8]。

由于其自由度需求,机器人通常需要多个关节驱动器以达到空间目标位姿。根据驱动器与关节数量之间的关系,可将机器人分为完全驱动和欠驱动两种。在双足机器人领域中,传统机器人利用稳定轨迹约束实现静态行走,行走速度低、能耗大;而欠驱动机器人能够利用自身重力和惯性实现动态行走,拥有更高的能量利用效率[9]。欠驱动双足机器人主要有点足式机器人和被动脚踝式机器人。Pratt 等[10]使用虚拟模型控制（Virtual Model Control,VMC） 方法在点足式机器人Spring Turkey 上实现二维行走,但由于缺少脚踝,行走稳定性依赖初始条件及虚拟约束参数等。Grizzle等[11-13]应用虚拟约束（Virtual Constraints,VC） 和混合零动力学（Hybrid Zero Dynamics,HZD） 方法将Rabbit 机器人视为五连杆结构,行走过程被建模为混合动力系统,在实机上实现了二维行走与奔跑。此后,MABEL、MARLO 机器人先后被研制。其中,MABEL 应用HZD 方法可以实现平面内动态行走[14];而MARLO 腿部为四边形并联结构,质量集中在机身部分,可以简化为线性倒立摆（Linear Inverted Pendulum,LIP）模型[15],通过应用步态库实现了三维空间中的稳定行走[16]。

欠驱动点足式双足机器人的研究难点在于:1）机身的大惯性对机器人行走稳定性造成干扰,因此需要避免机器人机身在运动过程中前后侧翻;2）被动式脚踝无法为身体提供扭矩,因此需要通过持续切换支撑腿维持机体稳定。本文基于一种并联五连杆点足式双足机器人,首先给出了五连杆结构的运动学模型。其次,基于LIP 模型设计了一套稳定控制方法,在单腿支撑阶段采用PD 反馈控制对机器人质心轨迹进行跟踪,在双腿切换阶段采用轨道能量方法计算捕获点即稳定落脚点位置,对机器人行走实现闭环控制。最后,结合实物模型,在Matlab 中实现了二维空间内的稳定性行走实验,并展示了行走过程中质心和控制关节角度的相轨迹图,证明了控制方法的有效性。

1 五连杆点足式双足机器人结构设计

双足机器人腿部结构决定了其运动性能,结构的静态和动态性能指标对机器人控制具有决定性作用。现有双足机器人如Atlas[6],大都是仿人体设计的串联腿部结构,负载能力较差。本文研究设计了一种并联五连杆腿部结构,并在腿部加入弹簧阻尼器以增加系统柔顺性,具体结构如图1所示,主要由机身、髋关节电机组、大腿杆件组、小腿杆件组等组成。当机器人运动时,髋关节电机组中横滚电机为机器人腿部提供横滚自由度,俯仰电机组为腿部提供俯仰自由度,五连杆机构实现力及运动的传递。

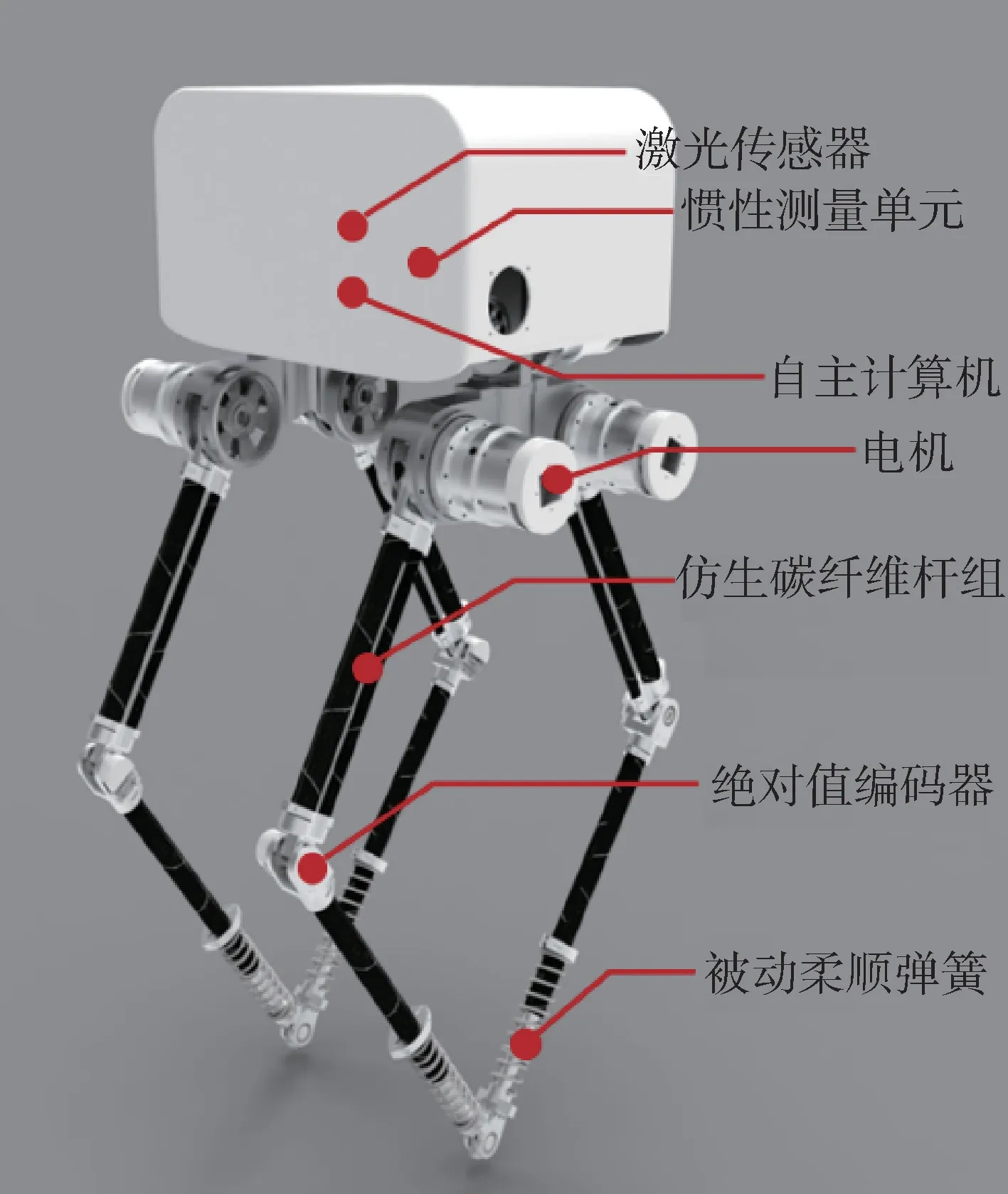
图1 并联五连杆机器人结构示意图Fig.1 Structure diagram of parallel five-link robot

该双足机器人相较于其他结构具有以下优点:

1）负载能力强: 五连杆并联结构相较于串联结构具有高负载能力,单腿最大载重可达30kg,整机最大载重可达70kg,预期搭载一名成年人或多种设备与物资,以满足伴随保障、物资运输等需求。

2）足端惯量低: 机器人大部分质量集中于上部机身,足端惯量低,如图2所示。在行走过程中降低足端对身体姿态的干扰,并且使实物更加贴近简化的数学模型,降低控制难度。

3）能量效率高: 采用五连杆对称结构,力矩传递指数高,欠驱动机器人能够利用自身重力和惯性实现动态行走,拥有更高的能量利用效率。

2 正逆运动学模型解算

机器人的运动学分析是进行机器人行走控制的基础。为了研究足端位置与输入电机角度之间的关系,本节分析了非同轴五连杆结构的运动学模型。首先给出了简化串联机构模型的变换矩阵,然后通过五杆闭链系统推导出角度映射关系,得到该模型的正逆运动学方程。

2.1 正运动学建模与分析

由于并联结构运动学难以分析,且很难找到所有并联结构的奇异位形,因此本文将五连杆结构简化为2 自由度串联结构,如图3所示。采用D-H 法则对该串联结构进行运动学分析。

图3（a）所示的并联结构中,将连杆长度依次设为l1～l5,五连杆内部关节角度依次设为θ1～θ5,髋关节侧翻角度设为θ6,其对应的串联结构如图3（b）所示,连杆长度与图3（a） 相同,对应角度设为φ1、φ2、φ3。选取上部连杆的中心作为基座坐标系（定义为0 坐标系）,从基坐标开始依次给所有关节编号,求解坐标系之间的变换关系,最终得到足端坐标系到基坐标系的变换矩阵

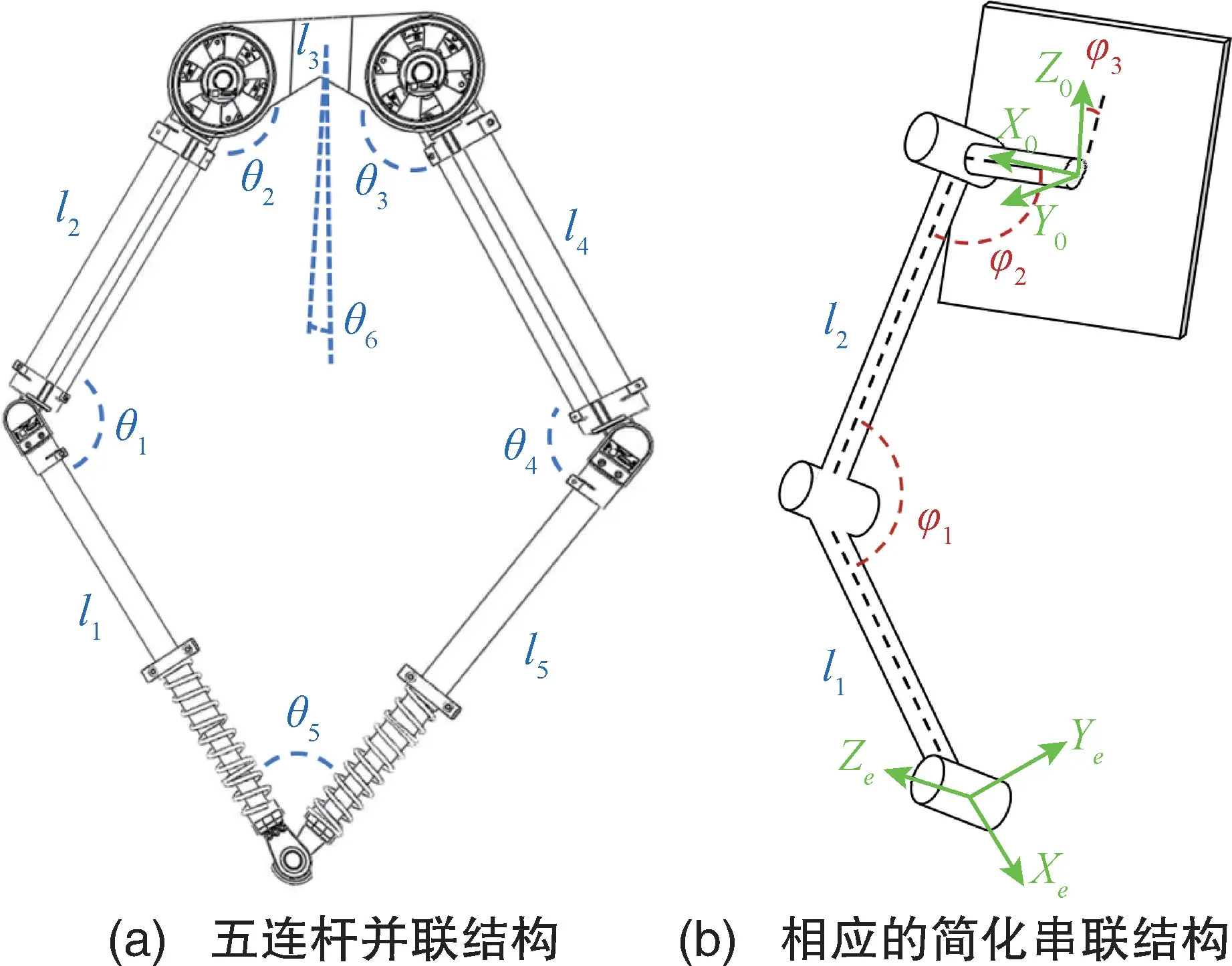
图3 并联五连杆结构及其对应简化串联结构Fig.3 Diagram of parallel five-link structure and its corresponding simplified series structure

式（1）中,nmT为从n号坐标系到m号坐标系的变换矩阵。

2.2 逆运动学建模与求解

逆运动学是指已知末端状态位置和姿态,求解各个关节角度的过程。对于该五连杆机器人,主要关心的问题即为通过足端与基坐标系的位置关系,反解出所需要的髋关节两个电机的角度即θ2与θ3。

首先,通过2.1 节串联结构下的变换矩阵,当足端位置相对于基坐标系的坐标为（x,y,z）时,有

由此可反解出此时的φ1、φ2、φ3分别为

求得φ1、φ2即图3（a）五连杆模型中的θ1、θ2后,根据五边形约束方程,求取两个髋关节角度θ2、θ3。非同轴五连杆的闭合方程如下

最终得到五连杆模型中的角度如下

式（5）中,

最终,可得到当足端想要到达（x,y,z） 坐标位置时的髋关节电机执行角度θ2、θ3。

3 双足机器人步态规划

3.1 基于LIP 模型的质心轨迹生成

本文所研究的机器人机身质量占总体质量的86.5%,故可将其简化为LIP 模型,LIP 模型动力学方程如下

式（7） 中,g为重力加速度,x为质心水平位置,h为恒定的质心高度,p为足端着陆位置（即行走过程中每一步的输入）。

LIP 模型为线性系统,对于连续行走来说,给定足端位置p,在经摆动时间T后,质心状态可以描述为一个离散系统,设k为机器人行走过程中第k步,则可将系统描述如下

式（8）～式（10）中,ω=式（8）中的pk对应为行走步态中第k步足端着陆点,通过给定pk可以获得质心轨迹x（t）。

3.2 基于贝塞尔插值的摆动腿轨迹生成

在机器人行走过程中,摆动腿末端轨迹对机器人行走至关重要,足端与地面碰撞产生的作用力会对机器人行走产生扰动,导致机器人关节驱动器难以有效跟踪期望位置。本文基于贝塞尔曲线生成摆动腿轨迹,贝塞尔曲线方程如下

式（11）中,t为自变量,M为贝塞尔多项式阶数,bi为支撑点的系数。

由于已知位置点只有足端起始点与足端终点,因此简单地采用了2 阶贝塞尔曲线生成摆动腿足端轨迹。通过选取起始点、终点与（pk为迈步长度,zm=0.2m）处三个点进行插值,获得的足端轨迹结果如图4所示。

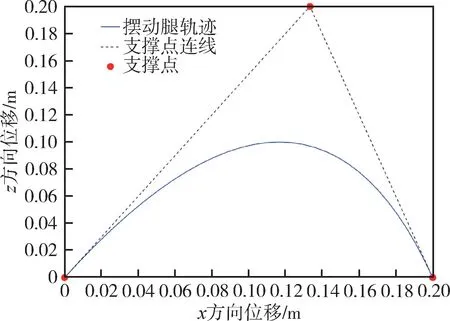
图4 平面内摆动腿轨迹Fig.4 Trajectory of 2D swing leg

4 行走过程的运动控制

上述章节中介绍的双足机器人步态轨迹是在理想环境下生成的,然而在真实场景中,机器人机身的大惯性与足端落地冲击会对机器人行走稳定性造成较大影响。因此,为达到机器人稳定行走的目的,本文在单腿支撑阶段采用PD 反馈控制对机器人的质心轨迹进行跟踪,在双腿切换阶段采用轨道能量方法计算捕获点即稳定落脚点位置。

4.1 基于PD 反馈的质心轨迹跟踪控制

在双足机器人每一步迈步过程中,由于机身的大惯量,在重力影响下机器人会出现前后倾倒现象,从而导致在正确计算各个关节位置情况下,机器人实际的质心轨迹也很难遵循倒立摆模型生成的质心轨迹。

为了克服上述问题,本文在此采用PD 反馈控制

式（12） 中,xn、、、、分别为n时刻矢状面上x方向的实际位置、期望位置、给定位置、实际速度和期望速度,zn、zrefn分别为n时刻矢状面上z方向的实际位置和期望位置,kp、kd、kz为对应的系数。

如图5所示,首先依据LIP 模型生成的质心轨迹和贝塞尔插值生成的摆动腿运动轨迹,得到该时刻期望位置,根据逆运动学求解出当前状态的关节角度,控制双足机器人做期望运动。通过陀螺仪、加速度计等传感器实时获取机器人机身位置、速度轨迹即xn、、zn,与期望轨迹做差,乘以相应的系数kp、kd、kz,补偿到下一时刻机身与足端相对位置的输出上,使得机身保持水平运动,成功跟踪上节中生成的质心运动轨迹,实现稳定的LIP 运动。

图5 迈步过程PD 反馈控制框图Fig.5 Block diagram of PD feedback control in stepping process

4.2 基于轨道能量的捕获点计算

在双足机器人行走过程中,由于在足端落地瞬间地面会对机器人产生冲击,如果离线给定机器人期望迈步长度,会使其在前进过程中摔倒。同时在每两步之间切换时,摆动腿期望落点位置决定了下一步态周期机器人初始状态。

轨道能量是一种假想的势能,用来描述机器人质心的运动状态,定义为

式（13）中,x、z分别为质心在矢状面上相对于支撑点的水平位置和高度,为质心水平速度,g为重力加速度。在线性倒立摆运动中,轨道能量守恒,因此在双腿切换过程中,通过控制摆动腿的落点以获得期望的轨道能量,从而获得期望周期步态。

捕获点[17]最初是基于目标轨道能量为0 提出的,使得其在受到外界干扰以后能够获取一个动态平衡的控制过程,从而保证控制倒立摆模型的平衡[18]。但在实际应用过程中,可以通过设定目标轨道能量E来实现机器人稳定前进的效果,其计算方法如下

式（14）中符号定义与式（13）相同,sign（·）为符号函数。当x>0 时,sign（x）=1;当x=0 时,sign（x）=0;当x<0 时,sign（x）=-1,可根据当前质心的速度方向来决定。

结合上述两种算法,得到初步的控制框图如图6所示。系统输入为质心的目标位置和速度（xref、）,反馈输入为机器人的整体状态（图中的“机器人状态”）,机器人状态包括四个膝关节的关节角度、腰部的状态（位置和姿态）、腰部的速度和角速度。根据这些输入计算当前落足点的优化位置,并分别用LIP 和贝塞尔插值法计算支撑腿和摆动腿的轨迹。该控制器对机器人实现了一个闭环控制,改善了离线轨迹生成算法在鲁棒性和控制精确度等方面的问题,确保机器人能够实现稳定行走。

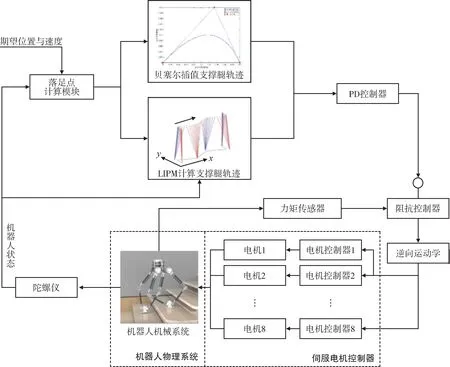
图6 机器人稳定行走控制简图Fig.6 Schematic diagram of robot stable walking control

5 仿真实验

在Matlab 中利用Simscape 模块搭建仿真系统:首先通过solidworks 设计装配体,构建与真实机身结构相同的双足机器人模型,生成整机的urdf 文件;其次将urdf 模型导入至Simulink 中,通过使用关节等模块建立机械部件之间配合、约束关系的运动学约束,并确定各个关节参考系;最后利用Multibody Contact Forces Library 库调整参数模拟重力与接触力碰撞,以达到真实的物理环境。

在此过程中,通过为机身装载惯性传感器模块（即陀螺仪与加速度计）,为关节装载编码器模块,实时获取机器人的四个状态。图7展示了仿真系统中搭建的机器人整机系统,表1展示了机器人模型参数。

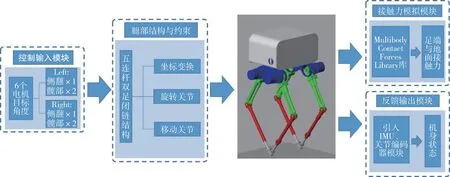
图7 机器人整机系统的搭建示意图Fig.7 Schematic diagram of the whole robot system

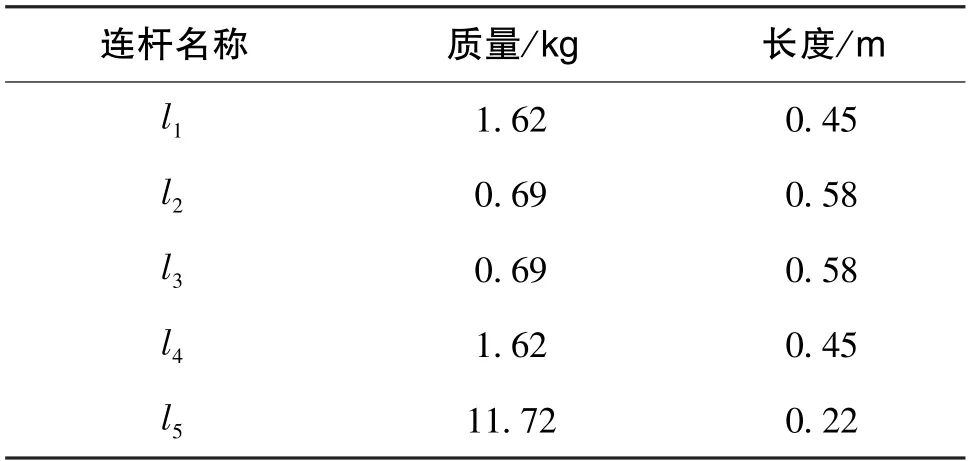
表1 机器人模型参数Table 1 Parameters of robot model

对行走过程进行仿真,反馈控制参数为kp=0.19、kd=-0.15、kz=-0.01。图8为机器人行走过程截图,可以看到机身有少许的向后倾倒,但并没有妨碍机器人的稳定行走。图9为机器人行走过程中前部和后部髋关节电机的相轨迹图。图10为机器人行走过程中质心速度随时间的变化曲线,可以看出,双足机器人在经过一段时间后可以达到一个相对稳态,在仿真中实现了以一定速度向前行走的效果。

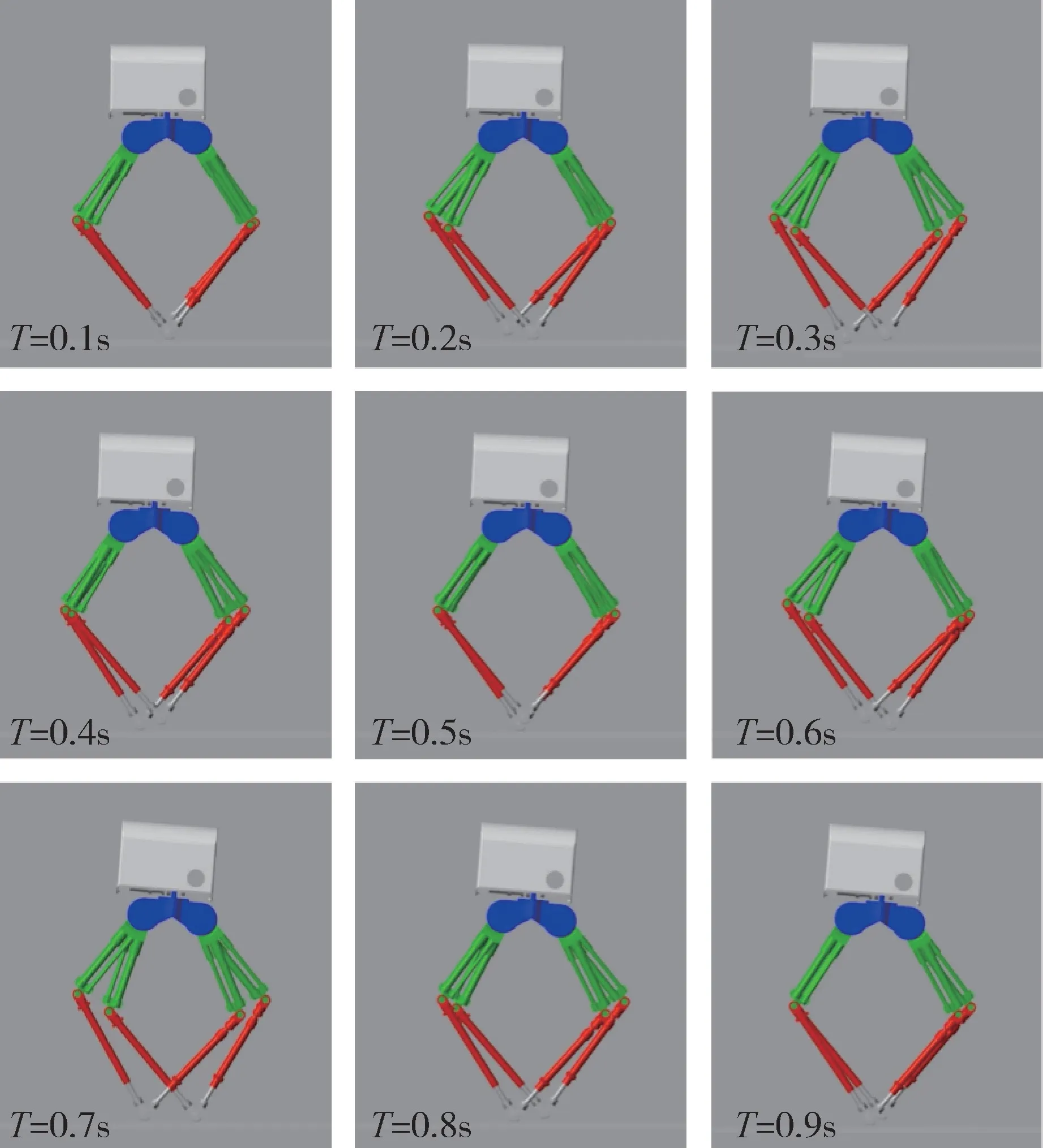
图8 机器人行走仿真截图Fig.8 Screenshot of robot walking simulation

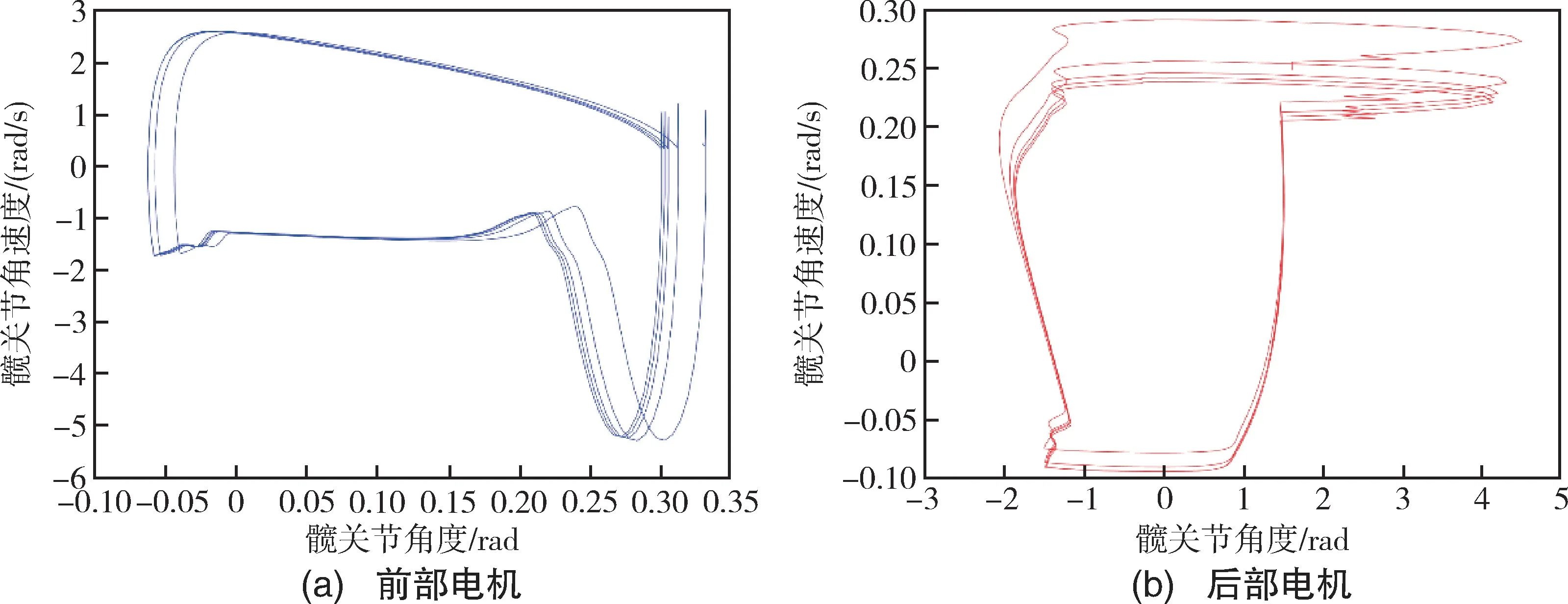
图9 髋关节电机的相轨迹图Fig.9 Phase trajectory diagram of the hip joint motor

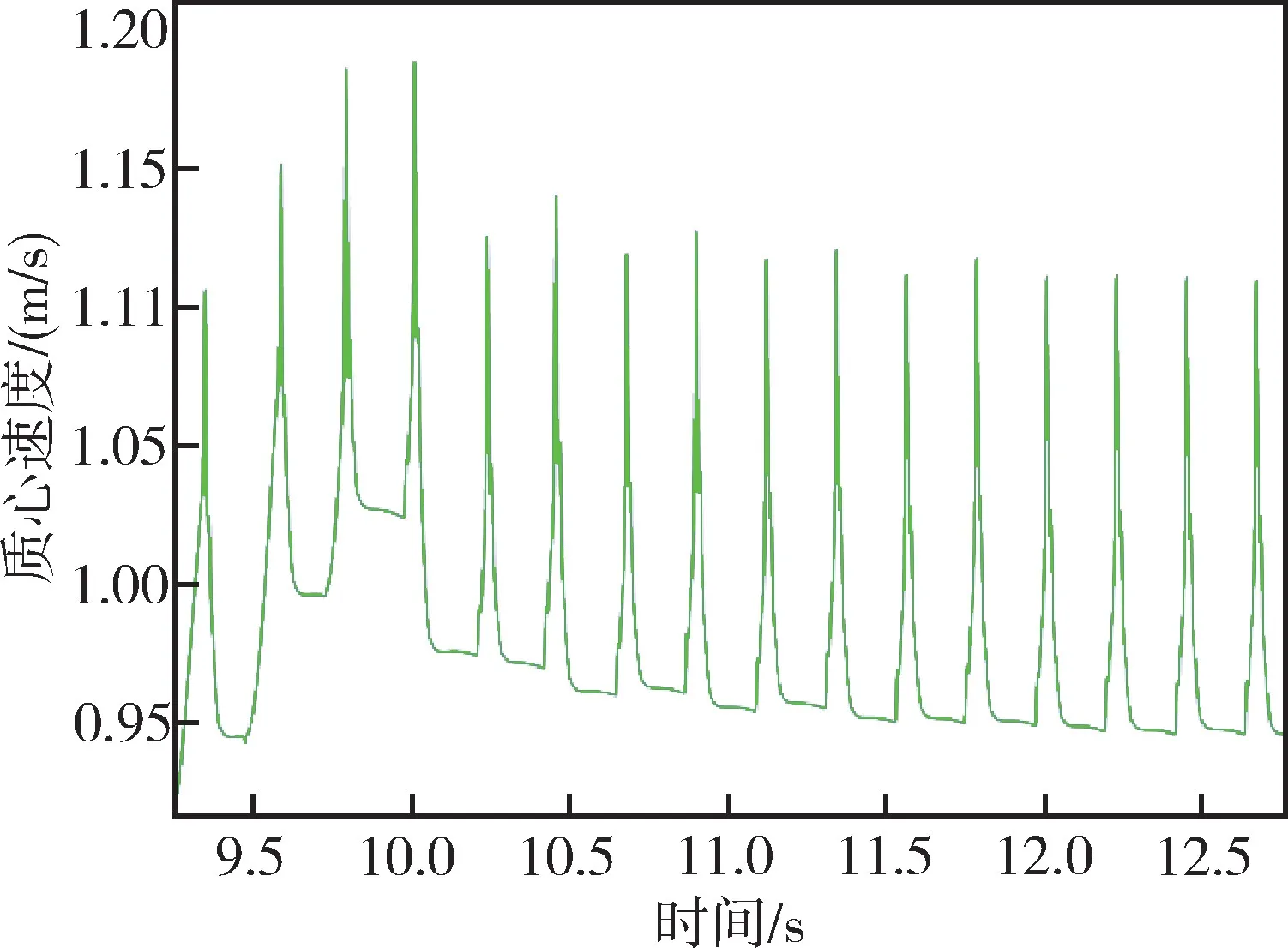
图10 机器人质心速度曲线（一段时间后趋于周期性稳定）Fig.10 Curve of robot centroid velocity （cyclically stabilized after a period of time）

6 结论

针对点足式双足机器人,本文提出了一种并联五连杆结构,并基于该结构进行建模。通过正逆运动学分析,将LIP 模型与PD 反馈控制进行结合,对机器人质心轨迹进行跟踪,并且根据实时反馈的自身状态计算稳定落脚点位置,实现闭环控制。结合实物模型构建Matlab 仿真实验,验证了控制算法的有效性,未来预期将本文所述控制方法用于实体机器人的二维矢状面行走控制。