基于抖动信号注入的微机电陀螺量化噪声抑制技术

李青松,王 鹏,肖定邦,吴学忠

（国防科技大学智能科学学院,长沙 410073）

0 引言

陀螺仪作为一种惯性传感器和执行元件,是角速度测量和惯性导航等应用的重要组成部分[1]。因其小体积、低功耗、低成本等优点,微机电（Micro Electro Mechanical Systems,MEMS）振动陀螺在无人系统、汽车、移动载体等领域具有广泛的应用前景。零偏稳定性是评价微机电振动陀螺性能的重要指标,其与零偏输出的噪声直接相关。随着陀螺品质因数不断提升,谐振器自身的机械热噪声随之减小[2],零偏输出噪声越来越受限于电路噪声。在由数字电路构成的控制系统中,量化噪声是电路噪声的重要来源。因此,抑制量化噪声对于提升零偏性能具有重要意义。增大数模转换芯片的位数[3]、提高数据采样率[4]等方法均可以有效降低量化噪声,但基于硬件限制,数模转换芯片位数和数据采样率都是有限的,且过高的芯片位数和高采样率意味着更高的成本,因此有必要寻找一种简单低成本的方式实现量化噪声的抑制。本文采用抖动信号注入技术[5],通过引入与陀螺模态无关的正弦抖动r信号,降低了量化噪声在陀螺工作频率处的能量,从而实现了量化噪声的抑制。该方法在蜂巢式微机电陀螺上进行了验证,实验表明: 施加抖动信号后,系统零偏稳定性得到有效提升,从0.24（°） /h 减小至0.08（°） /h,取得了较好的效果。该方法同样适用于其他微机电陀螺的测控系统。

1 蜂巢式微机电陀螺系统的量化误差分析

1.1 蜂巢式微机电陀螺结构与工作原理

蜂巢式微机电陀螺的思路源于自然界的蜂巢式拓扑结构,通过提取其圆环区域的正六边形蜂巢型结构,并经过适当的变形得到[6]。如图1（a）所示,蜂巢式谐振结构整体呈周向45°对称,最外侧为完整圆环,内部为变形的六边形结构按照蜂巢拓扑结构进行排列,并通过位于中心的锚点固定。谐振结构中分布着六边形的孔隙,可用来设置电极或挂载集中质量块。如图1（b）所示,蜂巢式谐振结构和多环谐振结构相同,均工作在n=2 模态。

图1 蜂巢式微机电陀螺结构与工作模态Fig.1 Structure and operating modals of the honeycomb disk resonator gyroscope

蜂巢式微机电陀螺是一种典型的工作在简并模态的微振动陀螺,其工作原理为: 通过静电力驱动方式,以特定的频率激励出谐振结构如图1（b）所示的第一模态（即驱动模态）,当有轴向角速度输入时,谐振结构在哥氏力的作用下产生如图1（b）所示的另一固有刚性轴系的第二模态（即检测模态）,谐振结构第二模态的振动通过电容检测方式转换成敏感电信号,该敏感电信号与输入角速度成正比,经过滤波及放大等处理即可得到输入角速度信息。

1.2 蜂巢式微机电陀螺控制系统

作为一种高精度的速率陀螺,蜂巢式微机电陀螺常采用力平衡控制模式[6]。如图2所示,陀螺驱动模态的振动通过锁相环（PLL）锁定在谐振频率,同时利用幅值控制保证陀螺驱动模态的恒幅振动;检测模态的位移在力平衡模式下实时被抑制,其中正交误差通过调轴回路实时输出的调轴电压消除,同相回路的哥氏力则被力反馈电压实时抵消。同相回路PID 的输出信号是陀螺的测量输出。

图2 蜂巢式微机电陀螺控制系统框图Fig.2 Control system block diagram of the honeycomb disk resonator gyroscope

1.3 量化噪声对陀螺输出的影响

由图2中陀螺控制系统可知,系统由数字和模拟两部分组成,由于D/A 和A/D 的量化过程,使得系统不可避免地存在量化误差,而这些误差最终均会反映在陀螺的输出中。

对陀螺检测模态的同相回路进行噪声分析,其框图如图3所示。K1为两个模态的哥氏耦合系数,G（s） 为检测模态的等效传递函数,Kc为C/V转换,H（s）为电荷放大器后到进入数字板之前的传递函数(一般可能包括低通滤波器等模块),Kb为放大系数,反馈环节HF（s）为解调模块、PID 模块以及调制模块的综合传递函数,Ks为反馈力系数。图中引入了四个噪声来源,N1为电荷放大器引入的噪声,N2和N3分别为A/D 和D/A 引入的量化噪声,N4为陀螺机械热噪声。

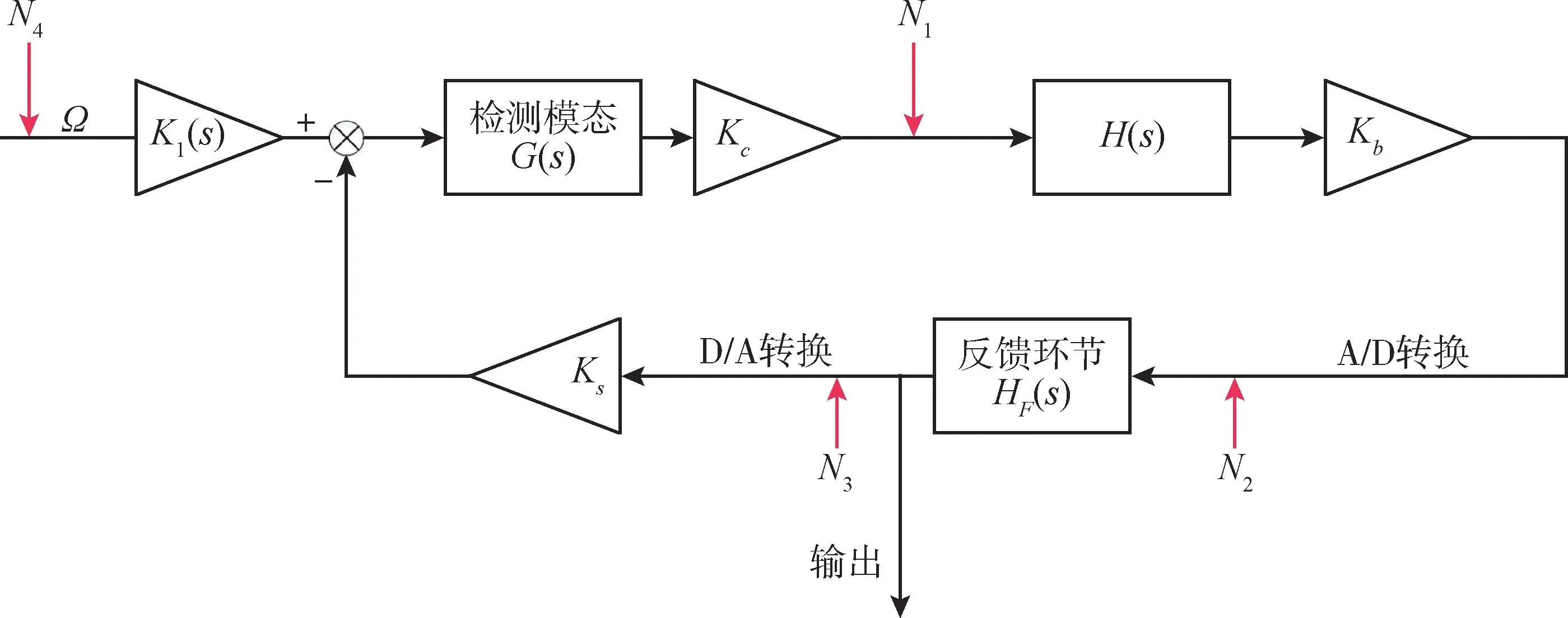
图3 检测模态力反馈环路框图Fig.3 Block diagram of force rebalance loop on the sense modal

计算图中的闭环系统表达式,可以得到

通常,对于电路设计而言,HHFGKsKcKb≫1,则式（1）可以化简为

由此可以得到系统输出零偏为

由式（3）可知,量化误差最终会在陀螺输出中引入新的噪声,该噪声的影响可以通过减小Ks、增大Kc和Kb以及减小频差提升G（s）来进行抑制,但由于运放量程的限制,使得增益不能无限大,因此需要寻找其他的方法来减小量化噪声的影响。本文通过引入抖动信号的方式极大地减小了式（3）中N2和N3的大小,从而避免了对系统增益的更改。

2 基于抖动信号的量化噪声抑制技术

2.1 量化噪声

连续的模拟信号在数字与模拟信号相互转化的过程中会变成离散的数字信号,由于对模拟信号的量化,使得转换前后的信号存在差异,导致量化噪声的出现,直接影响陀螺输出的性能。量化噪声在量程中变现为一个周期性的锯齿波[7],假设输入值为x,输出的量化误差为y,1LSB 代表的输出量为Q,则两者的关系如图4所示。由图4可知,量化误差的周期为Q。

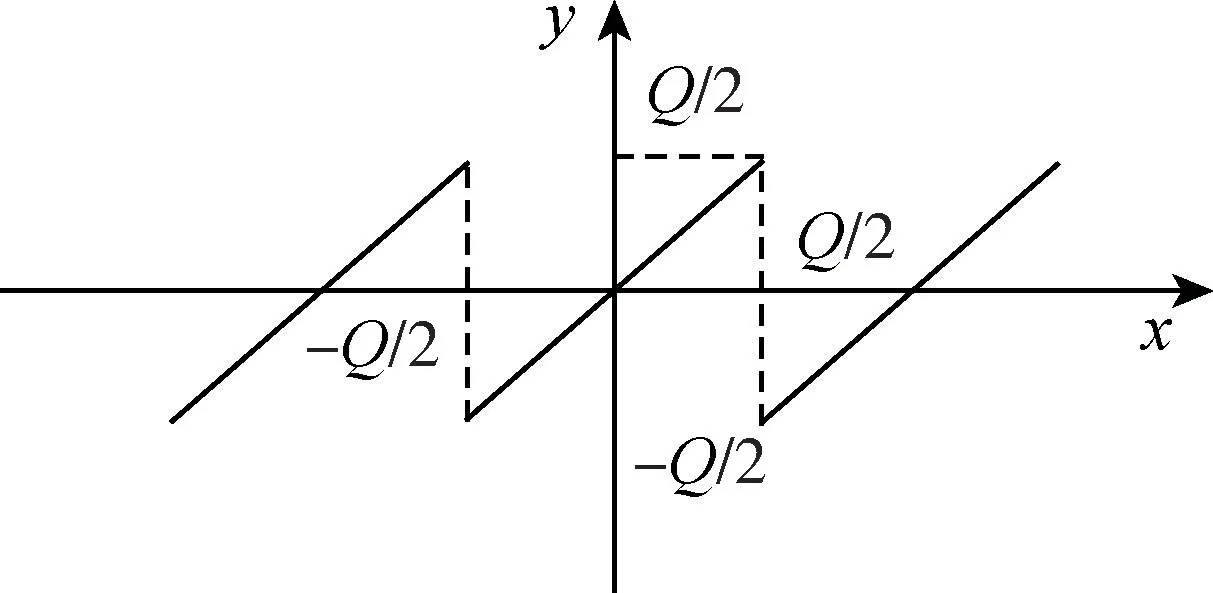
图4 量化误差Fig.4 Diagram of quantization errors

显然量化误差函数表达式为

对周期变化的y进行傅里叶展开,可以得到

如图5（a） 所示,1MHz 采样频率的ADC 或DAC 对一个频率为4260Hz 左右的小幅值信号进行量化,可以发现量化前后信号严重失真,其量化噪声如图5（b） 所示,噪声表现出明显的周期性,且该周期与输入信号频率相关,从而在工作频率处引入量化误差,最终反映在陀螺输出上。

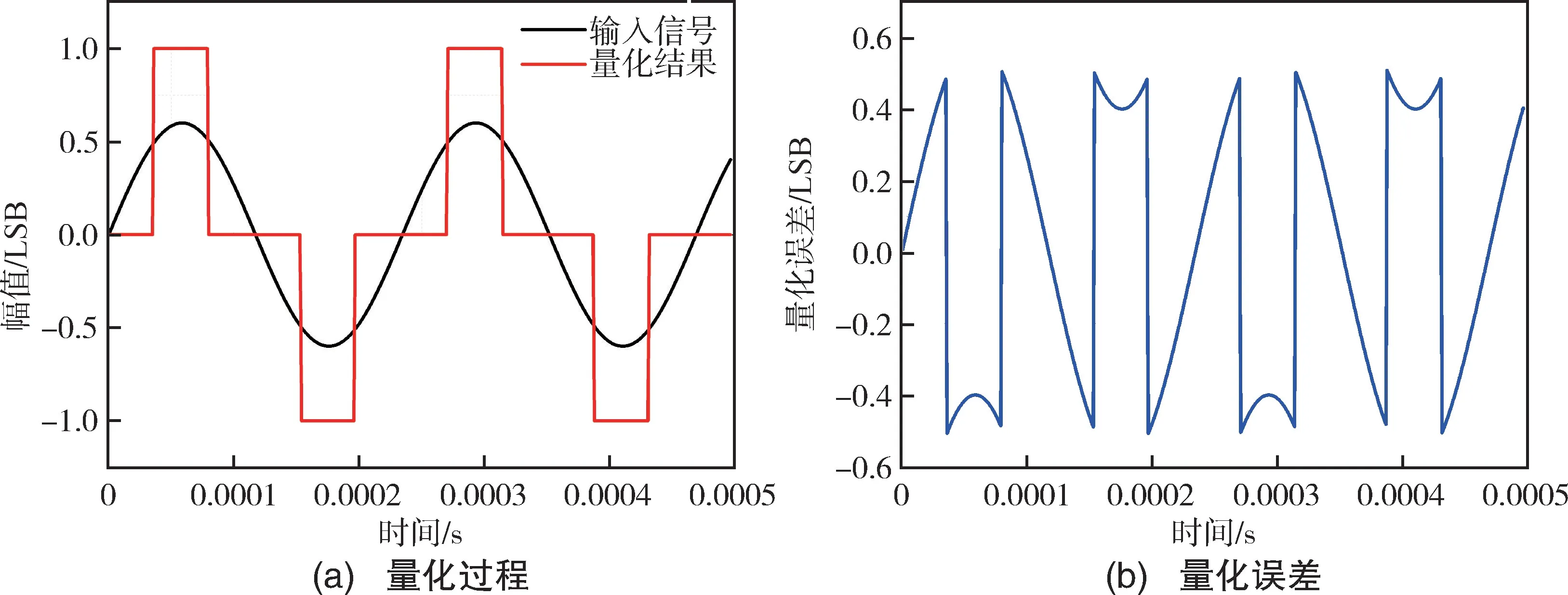
图5 小幅值信号的量化过程Fig.5 Quantifying process of the signal with a small amplitude

对于蜂巢式微机电陀螺这类高Q值对称陀螺,其零偏一般很小,则零偏输出的量化噪声将会很大。例如,对于零偏均值为0.01（°） /s、噪声峰峰值为0.002（°） /s 的输出,假设输出为16 位DAC,满量程代表±500（°） /s,则零偏理想输出范围为0.524LSB～0.786LSB,然而量化后为1LSB,从而导致输入误差。

2.2 正弦抖动信号下的量化噪声

在图2的控制系统中,DAC 输出的反馈力信号是频率与驱动频率一致的正弦信号,陀螺输出为该正弦信号的幅值。假设陀螺的理想反馈力信号为

式（6） 中,f0为工作频率,A为零偏。根据式（5）可以得到量化误差为

对式（7）进行展开化简,可以得到量化误差的表达式

式（8）中,Jm（z）为m阶的贝塞尔函数,为奇数,当z越大时,Jm（z）越趋近于0。

通过量化噪声的时域表达式可以计算其功率谱为[8-9]

当m=1 时,脉冲信号的幅值表示工作频率处的噪声幅值,该值越大表明噪声影响越大。由于陀螺零偏A一般较小,使得脉冲信号幅值较大,即量化噪声在工作频率处的能量较大。为了减小量化噪声在工作频率处的幅值,本文引入了一个已知幅值和频率的正弦抖动信号,假设该信号幅值为B,频率为fd,此频率应保证与陀螺的模态频率无关,避免对陀螺工作产生干扰。正弦抖动信号与反馈力信号叠加输出,其形式表示为

此时,新的量化误差为

计算其功率谱,可以得到

式（12） 中,m与r的奇偶性相反,当m=1、r=0 时,脉冲信号幅值为工作频率处量化噪声大小,显然相较于无抖动信号,此时幅值又乘了一个贝塞尔函数,通过选取合适的抖动信号幅值B（可设置为D/A 满量程输出的1/10）,可以使Jr（2nπB/Q）的值很小,进而减小最终工作频率处的量化噪声。

图6给出了施加抖动信号前后量化误差在工作频率（4260Hz）附近的频谱图。由图6可知,施加抖动信号前,量化误差在工作频率处有明显的幅值;而施加抖动信号后,该处量化噪声的能量迅速减小,由0.1036LSB 减小为0.0013LSB,表明了抖动信号对量化噪声有较好的抑制效果。

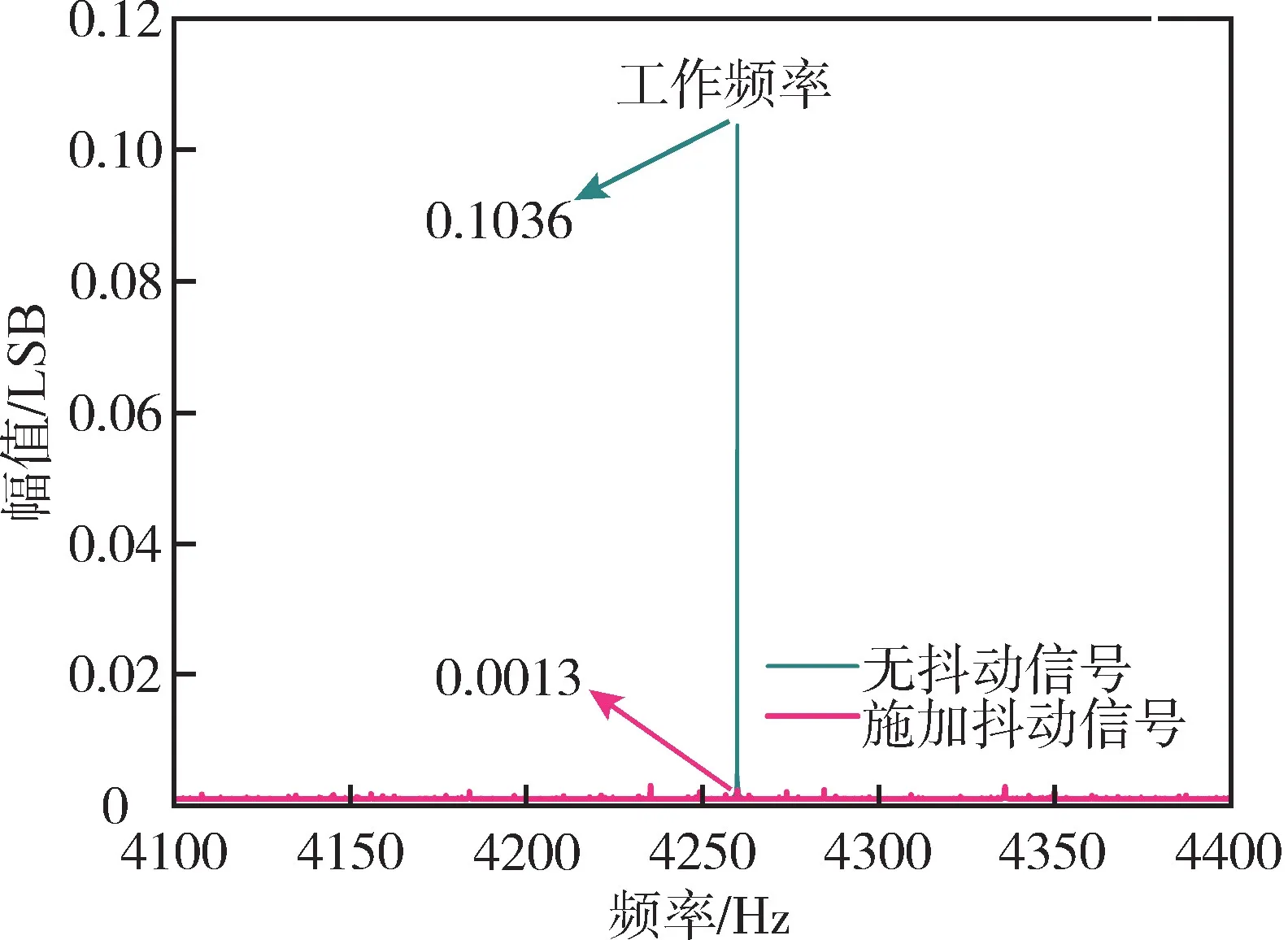
图6 施加抖动信号前后量化噪声频谱图Fig.6 Spectrum of quantization noise with and without the dither signal

3 实验验证

为了验证抖动信号对陀螺零偏噪声的抑制作用,本文利用数字电路测试了常温环境下蜂巢式微机电陀螺施加抖动信号前后的零偏输出,其结果如图7所示。由图7可知,施加抖动信号前,陀螺零偏噪声峰峰值为0.0024（°） /s,零偏稳定性约为0.24（°） /h;施加抖动信号后,零偏噪声显著减小,变为 0.0008 （°） /s,零偏稳定性提升至0.08（°） /h,性能提升了3 倍。该实验中,DAC 位数为16 位,施加抖动信号频率为1111Hz,幅值为128LSB,占总量程的0.4%左右,即牺牲0.4%的量程实现了噪声3 倍的提升。

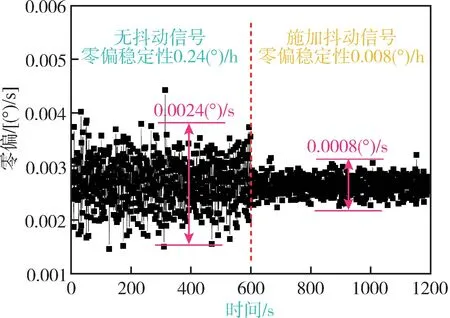
图7 施加抖动信号前后陀螺噪声变化Fig.7 Gyroscope noise with and without the dither signal

图8给出了施加抖动信号前后Allan 方差曲线对比。由图8可知,无抖动信号情况下,陀螺ARW 为 0.0096 （°） /h1/2,零偏不稳定性为0.05（°） /h;施加抖动信号后,ARW 减小为0.0039（°） /h1/2,零偏不稳定性提升了8.3 倍,减小为0.006（°） /h。

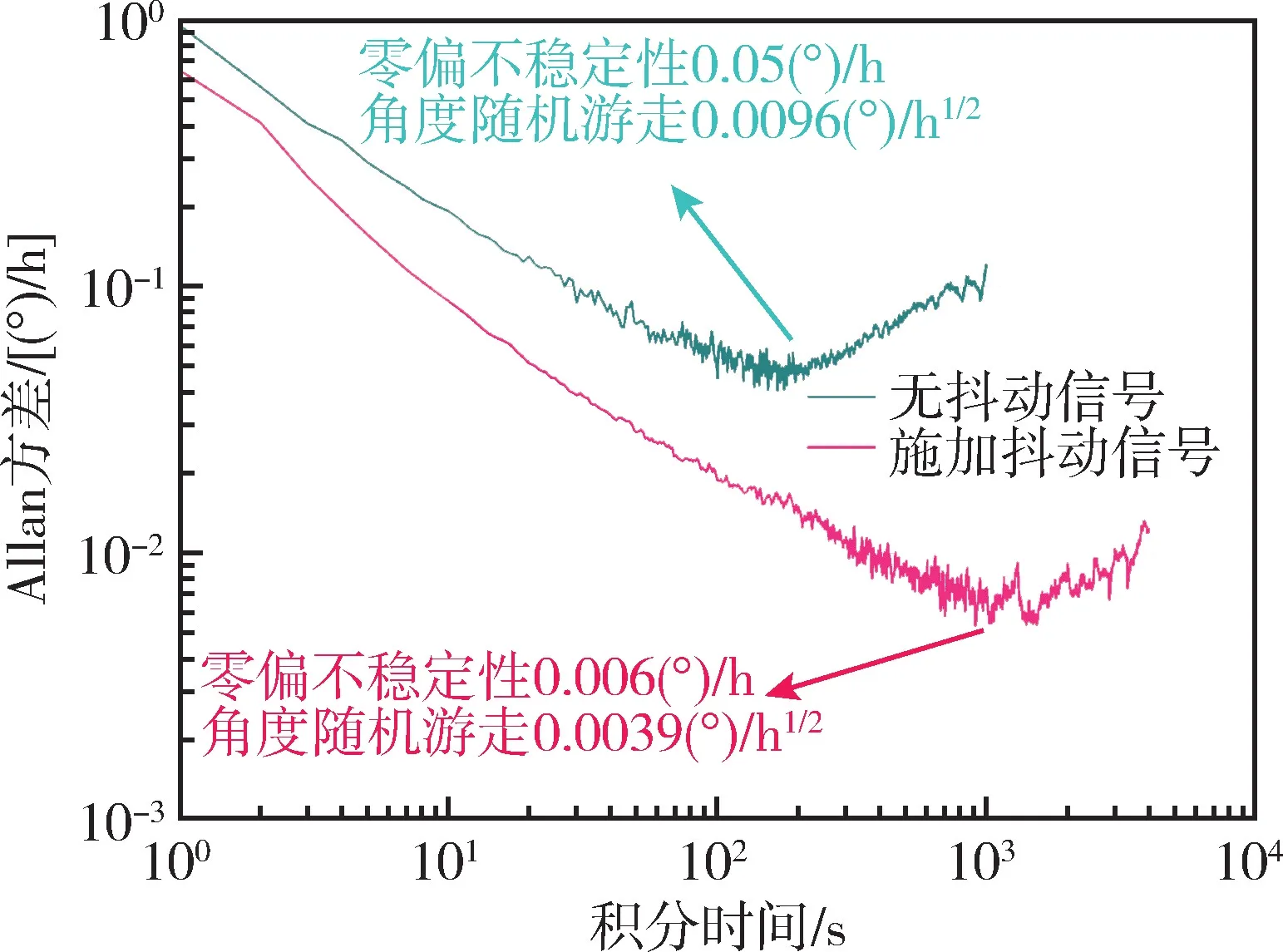
图8 施加抖动信号前后Allan 方差曲线Fig.8 Allan deviation with and without the dither signal

3 结论

为了抑制陀螺零偏输出中的量化噪声,本文采用了利用抖动信号减小量化误差的方法。该方法通过在陀螺系统反馈输出中叠加与陀螺模态频率无关的正弦抖动信号,降低了量化误差在陀螺工作频率处的能量,提升了零偏的性能。实验结果与理论分析基本一致,施加抖动信号后,零偏噪声显著减小,证明了该方法对量化噪声抑制的有效性。