基于虚拟旋转的速率积分型半球谐振陀螺锁区克服方法

白 帆,姚志强,刘珊珊,刘 聪

（中国航空工业集团公司西安飞行自动控制研究所,西安 710076）

0 引言

半球谐振陀螺（Hemispherical Resonant Gyroscope,HRG）兴起于20世纪60年代,是一种新型的哥氏振动陀螺,具有精度高、结构简单、可靠性高、体积小、质量小以及功耗低等优点,在国防、航空、航天、航海等领域具有重要应用价值,因此得到了广泛关注[1-3]。

半球谐振陀螺主要有两种控制模式,即速率模式和速率积分模式[4-5]。速率模式是指,当陀螺敏感到外界输入角速度时,谐振子的振型会相对壳体发生进动,通过控制电极实时施加反馈力,使四波腹振型不发生进动,即振型与壳体方向始终保持一致,再根据所施加的反馈力的大小得到要测量的角速度信息[6]。速率积分模式是指,谐振子的振型可以自由进动,振型进动的角度与载体转动的角度成比例关系,通过测量振型进动的角度就可以直接得到载体转动角度。速率积分模式下,振型可以自由进动,具有较高的带宽,能够满足大动态高机动性条件下的测角需求[7-8]。陀螺的闭锁效应是指,外界输入角速度小于陀螺的闭锁阈值时,陀螺无法准确敏感到外界输入的角速度。在半球谐振陀螺的制造过程中,由于制造工艺水平的限制,会带来许多的误差。其中,阻尼不均匀和频率裂解是造成陀螺闭锁误差的主要来源[9],这直接影响了陀螺的性能。

虚拟旋转法是指对半球谐振陀螺的控制电极施加静电驱动力,以驱动谐振子的振型虚拟旋转。文献[10]通过驱动振型虚拟旋转实现了模态反转,对零位进行校准,校准后零位下降,降低了测量误差。文献[11]对振型施加了6（°） /s～10000（°） /s 的虚拟旋转,结果表明,随着转速的增加,非理想半球谐振陀螺的进动因子越趋近理想值,即在测量高转速时表现更为出色。但是,这些文献只是对虚拟旋转法进行了一定程度的应用,并没有介绍工程中如何使用虚拟旋转法使速率积分模式陀螺克服锁区并工作在正常模态。本文首先理论推导了虚拟转速应用的必要性,在此基础上应用控制变量法研究了随外界输入角速度变化陀螺的闭锁状况,在速率积分型半球谐振陀螺控制方案的基础上,采用虚拟旋转方法,研究了虚拟转速对陀螺克服锁区的影响,对此进行了理论推导和仿真验证,并创新性地结合工程实际分析了可行性和操作方法。

本文结构如下: 首先,根据半球谐振陀螺谐振子动力学方程建立误差模型,给出了半球谐振陀螺的控制方法。其次,针对半球谐振陀螺的锁区问题,提出了一种驱动振型虚拟旋转的方法。最后,搭建Matlab Simulink 模型,验证了本文提出方法的有效性。

1 半球谐振陀螺理论基础

半球谐振陀螺在敏感到外界输入角速度时,它的振型会相对于其壳体反向进动,且其进动角度与外界输入角度成比例关系,通过测量方位进动角的变化,可以准确得到载体转动的角度,从而达到测角功能。理想情况下,方位进动角与外界输入角速度的关系为

式（1）中,θ为陀螺的进动方位角;k为进动因子,只由器件本身特性决定;Ω为外界输入角速度。

理想情况下,可以用一个质量块在二维空间中的简谐振动来等价描述半球谐振陀螺的力学等效模型[12],具体如图1所示。

图1 HRG 等效模型Fig.1 Equivalent model of HRG

Lynch 博士针对半球谐振陀螺应用了平均法的思想[13],将半球谐振陀螺的运动轨迹简化为图2所示的椭圆轨迹。图2中,椭圆长半轴a为主波波腹轴,短半轴q为正交波腹轴,θ为主波波腹轴的方位角,ω为谐振子的谐振频率,ψ0为质点运动的初始相位。

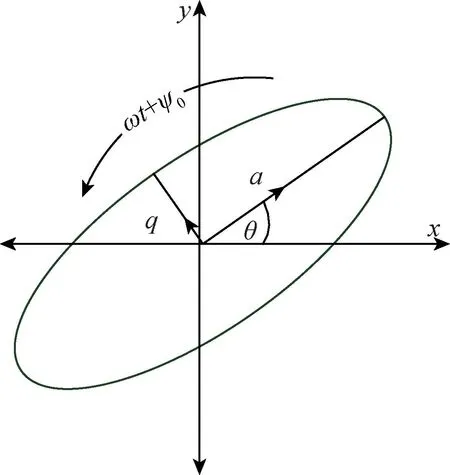
图2 椭圆轨迹图Fig.2 Diagram of elliptic trajectory

实际中,考虑到谐振子阻尼不均匀和频率裂解的存在,半球谐振陀螺的数学模型为[12]

根据Lynch 平均法,可得到

式（3）中,E为谐振能量,Q为波节点的振幅,θ为主波波腹轴的方位角,δφ为锁相误差,fas、fqc、fqs和fac分别为用于控制振幅、消除正交误差、控制振动方向以及控制振动频率的控制力。

速率积分模式下的半球谐振陀螺信号处理与控制系统由四个控制回路组成,分别为能量控制回路、正交控制回路、角度解算回路、锁相回路[14-15]。能量控制回路使谐振能量始终保持恒定;正交控制回路使陀螺敏感误差趋近于零;角度解算回路使陀螺能够自由进动,并实时输出进动角;锁相回路通过跟踪谐振子的固有频率,实现频率锁定的功能。半球谐振陀螺信号处理与控制系统框图如图3所示。

图3 HRG 控制系统框图Fig.3 Block diagram of HRG control system

2 基于虚拟旋转的控制方法

由于谐振子阻尼不均匀的存在,当外界小角速度输入时,阻尼不均匀产生的陀螺漂移会大于外界输入角速度,此时陀螺将无法正确跟踪外界输入角速度[16-17]。本文采用一种驱动驻波虚拟旋转的方法,使半球谐振陀螺在外界小角速度输入时也能精确跟踪外界输入角速度。进动角满足

在正交控制回路中,施加在离散电极上的静电力会消除频率裂解,使Δω无限趋于零,此时忽略频率裂解,研究阻尼不均匀对于进动角的影响。于是,式（4）可简化为

式（5）中,fqs为控制电极施加给半球谐振陀螺使驻波自进动的静电力,Ωvirt为施加fqs后引起的驻波虚拟角速度。

通过增加外界输入角速度,可以改善阻尼不均匀对陀螺漂移的影响[18]。此外,通过控制电极对谐振子施加一个远高于速率阈值的虚拟旋转Ωvirt,虚拟旋转Ωvirt是通过施加在控制电极上的静电力Fvirt产生的,外界输入角速度引起的真实进动角θtrue可以通过测量进动角θ减去虚拟旋转的角度得到

此时,施加在x和y方向上的驱动力为

引入了虚拟旋转的半球谐振陀螺控制系统原理框图如图4所示。

图4 加入虚拟旋转的HRG 控制系统框图Fig.4 Block diagram of HRG control system with virtual rotation

3 仿真验证

3.1 速率积分型半球谐振陀螺控制方案仿真

本文建立的Matlab Simulink 仿真模型如图5所示,由HRG 表头动力学、乘法同步检波、控制量计算、控制回路和驱动力计算模块组成。

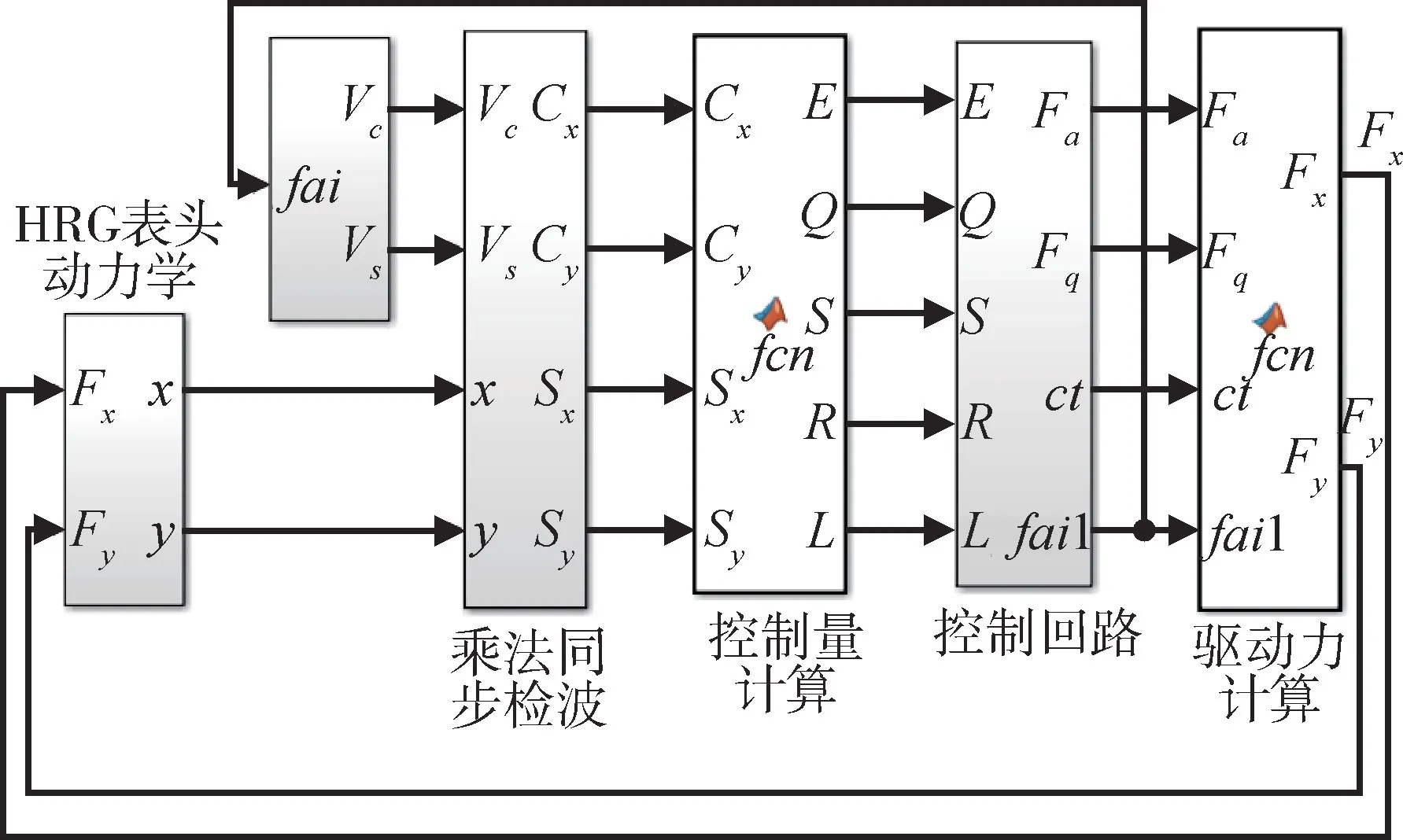
图5 HRG 控制系统Simulink 框图Fig.5 Simulink block diagram of HRG control system

本文仿真采用的参数如表1所示。

表1 仿真参数Table 1 Parameters of simulation

当外界输入角速度Ω=180（°） /s 时,半球谐振陀螺的仿真输出曲线如图6所示,此时的方位进动角θ随时间变化关系如图7所示。仿真结果表明,x轴、y轴信号的最大振幅始终为2V,不随时间衰减;x轴、y轴信号的频率始终保持谐振子谐振频率4430Hz;x轴、y轴信号的相位始终相差90°。因此,该控制方案能够使半球谐振陀螺的振幅稳定、相位稳定,方位进动角能够实时跟踪外界输入角速度。

图6 HRG 仿真响应曲线Fig.6 Response simulation curve of HRG

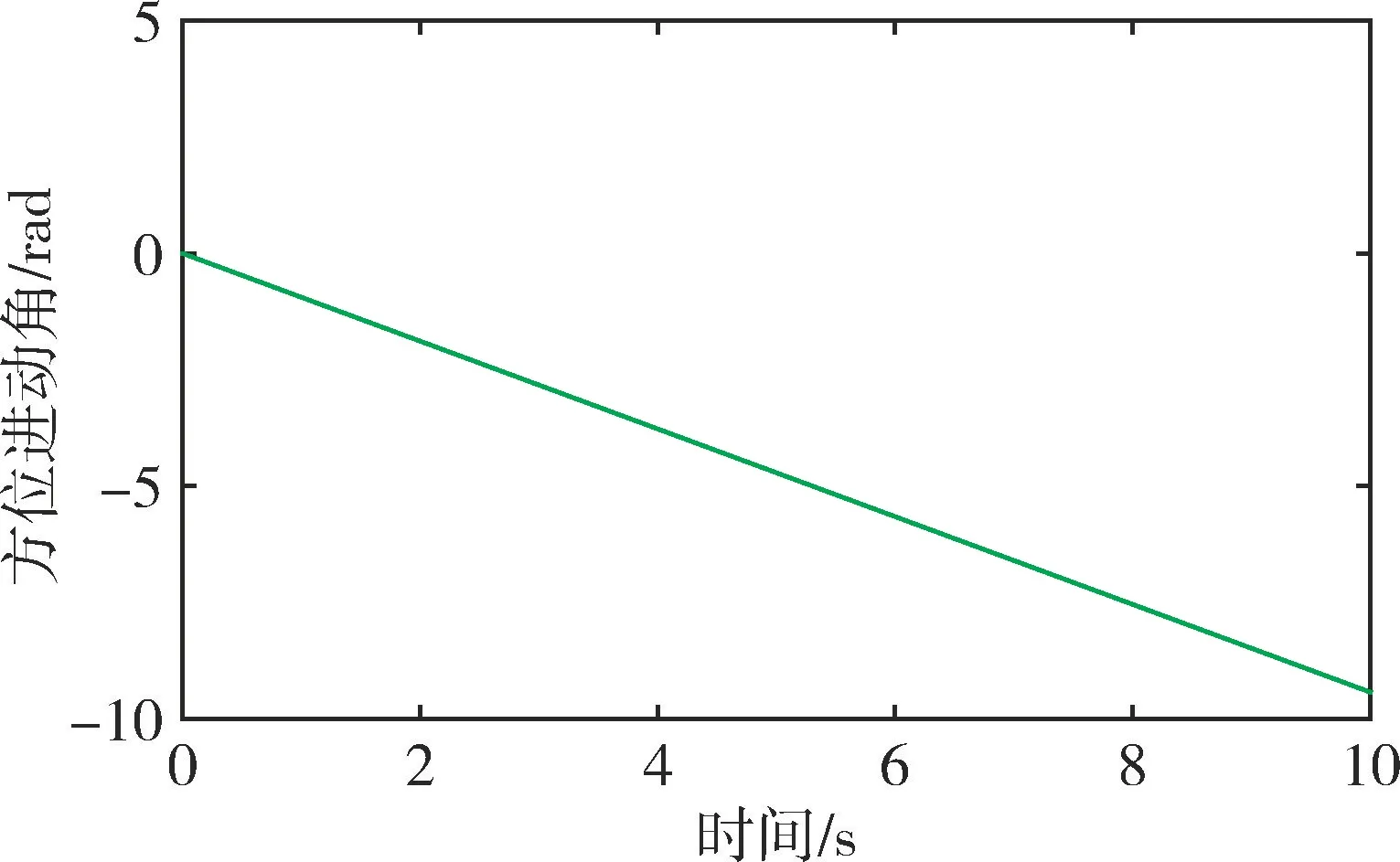
图7 方位进动角随时间变化关系Fig.7 Relationship between pattern angle and time

3.2 虚拟旋转法仿真

在速率积分型半球谐振陀螺控制方案的基础上增加虚拟旋转模块,Simulink 仿真模型如图8所示。

当外界输入角速度小于陀螺阻尼不均匀所导致的零位漂移时,如图9所示,令外界输入角速度Ω分别为0（°） /s、10（°） /s、20（°） /s 和40（°） /s,陀螺方位进动角均会闭锁在某恒定值,反映了HRG的闭锁效应。此时,为了使陀螺能够克服闭锁效应,给陀螺施加不同的虚拟转速,如图10所示。本文设计了一组对比仿真,对陀螺持续施加Ω=10（°） /s 的外界输入角速度,研究虚拟转速不同取值对陀螺克服锁区的效果。

由图10可知,当施加较小的虚拟转速Ωvirt=0.5πrad/s 时,进动方位角最终会收敛到某恒定值,此时仍然不能克服锁区的影响;当施加的虚拟转速为Ωvirt=πrad/s 时,进动方位角虽然不会收敛,但是其波动较大,严重影响了测角精度;当施加的虚拟转速为Ωvirt=5πrad/s 和Ωvirt=20πrad/s时,方位进动角随时间变化已经是一条平稳的直线,说明此时已经能够实时跟踪外界输入角速度,克服锁区的影响,实现测角功能。本文为提高计算效率,取阻尼不均匀=2rad/s,目前经过调平的谐振子阻尼不均匀能够抑制到0.1rad/s 以内,由可知,角速度阈值与阻尼不均匀成线性关系,即对于任一锁区内的外界真实输入角速度,理论上总会存在一个虚拟转速能够克服锁区。然而,当虚拟转速较小时,虽能够克服锁区,但此时方位进动角的波动会很大,测角精度差,如图10（b） 所示;当虚拟转速过大时,增加了控制的难度,还可能会引发其他误差。因此,在实际工程应用中,在理论计算的基础上,还应该进行进一步的测试,选择一个合适的虚拟转速。

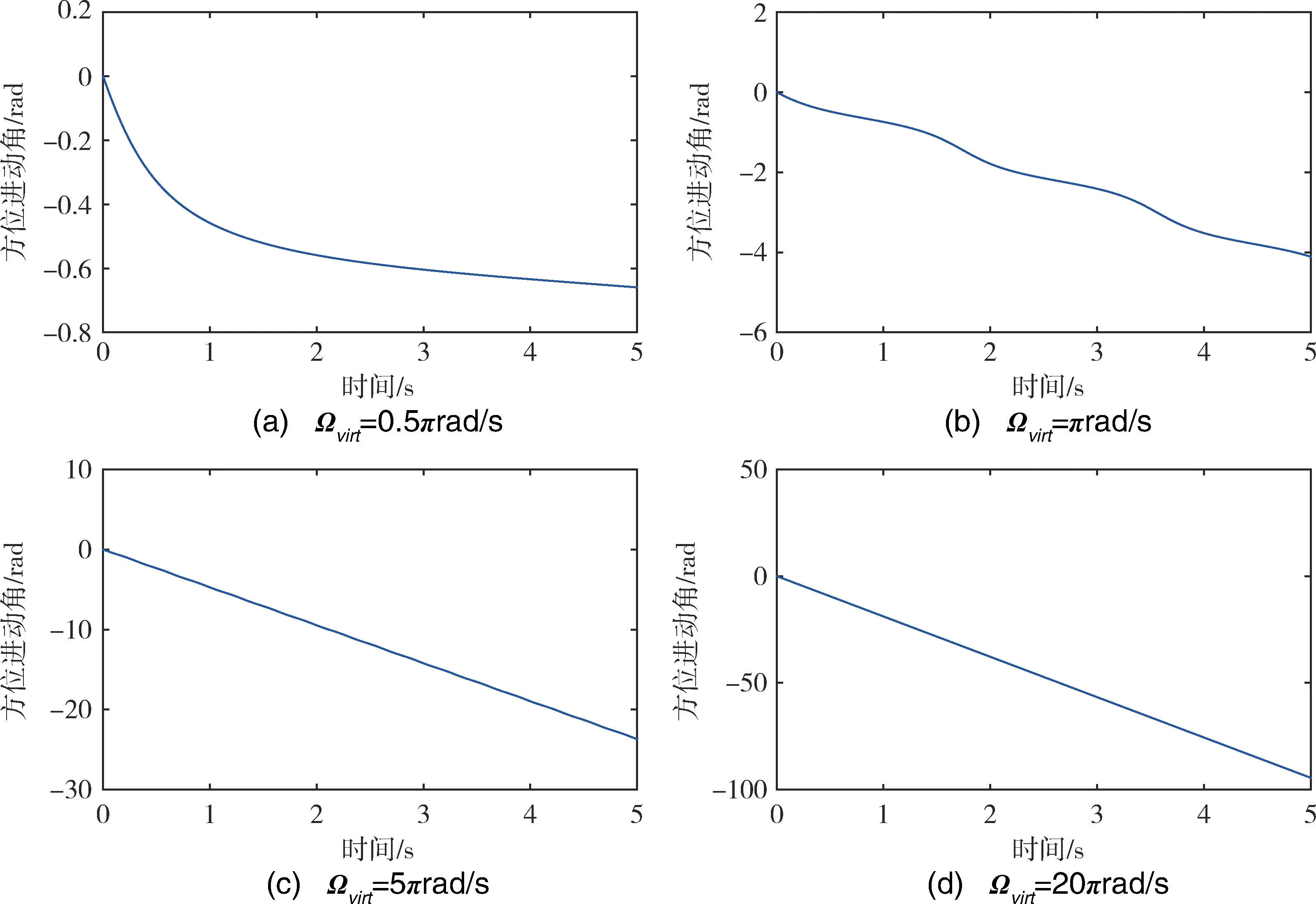
图10 虚拟转速不同取值对陀螺克服锁区的效果Fig.10 Results of overcoming lock-in effect with different virtual speed

4 结论

本文采用Matlab Simulink 模块建立了一种速率积分型半球谐振陀螺的控制方法,使陀螺在大动态环境下能够正常跟踪外界角速度并输出测角信息。针对外界小角速度输入时产生的闭锁效应,采用控制电极驱动谐振子振型虚拟旋转的方法,能够实现克服陀螺锁区的目标。结合目前现状,后续有望从以下两方面展开研究: 设计实验方案,验证本方案对克服锁区的作用,并回归理论和仿真模型,进一步验证模型的正确性;理论与仿真研究虚拟转速对陀螺漂移误差、零偏稳定性的影响,并设计实验进行相关验证。