基于雷达距离像的锥体目标进动参数估计方法
宁超,黄璟,朱勇,肖志河
(电磁散射重点实验室, 北京 100854)
0 引言
空间目标的微运动是指其整体或部件除质心平动以外的振动、转动等微小运动。微动在雷达回波中产生的多普勒称为微多普勒[1-2]。进动是中段弹头特有的微动方式,与目标形状结构、质量分布和动力学特性等物理属性密切相关。进动作为一种分辨真假目标的特征,受到广泛关注。有研究表明,弹道中段,弹头和诱饵的姿态运动差异较大,主要体现在进动周期、进动角等微动参数上,微动特征为非合作空间目标探测与分类识别提供了一条可行的途径,也成为了弹道中段目标识别研究的热点领域之一[3-5]。
弹道目标进动的进动特征主要包括进动周期和进动角。对于进动周期提取相对容易,而进动角特征提取难度大。国内,国防科技大学、西安电子科技大学、航天科工集团等多家单位开展了相关的研究,主要方法包括基于RCS幅度的提取方法、基于频谱特征的提取方法、基于雷达高分辨距离像的提取方法等,已有多篇文章文献刊出[6-9]。其中,文献[6]中提出了一种利用目标RCS的幅度值作为特征估计弹道目标的进动角的方法,而对于非合作目标难以预先获得其精确的RCS。文献[7]提出了利用时频分析提取进动参数的方法,但仅适用于目标零攻角飞行的情况。文献[8]提出用一维距离像序列估计进动参数,其方法也需要预知目标尺寸等作为先验信息。
本文提出了基于宽带雷达一维距离像的非合作锥体目标微动参数提取的新方法。首先得到目标的一维距离像(high resolution range profile,HRRP)时间序列,再根据雷达测轨信息,估计得到弹道中段目标的质心位置,联合使用目标质心位置与HRRP的径向长度特征,使用分步全局最优估计算法得到飞行进动锥体的长度、底面半径、进动角、进动周期等参数。该方法需要的先验信息少,对于非合作目标有较好的适用性。文中通过仿真数据验证了方法的可行性和正确性。
1 飞行中段进动目标HRRP径向长度特征
飞行中段的进动锥体目标的运动可以看作2种运动的合成:一是质心的平动,由天体力学可知,在近似真空的环境中仅受万有引力的作用,其运动轨迹为椭圆,该椭圆的一个焦点为地心,椭圆所在平面被称为飞行弹道面;另一种运动是锥体的进动,即由于初始冲量力矩的影响,产生的以固定的角速度绕其质心锥旋和自旋,本文考虑理想锥体目标,不考虑自旋对雷达回波影响。接下来,分2步进行讨论:先忽略平动,分析固定质心的进动对雷达回波的影响;然后再叠加平动,分析飞行中进动锥体的雷达回波特征。
1.1 固定质心的进动目标HRRP径向长度特征
考虑均匀的轴对称,长度为l,进动中心距离球顶为h,底面半径为b。设进动角为γ,进动速率ω,雷达视线与进动轴夹角为β。如图1所示。
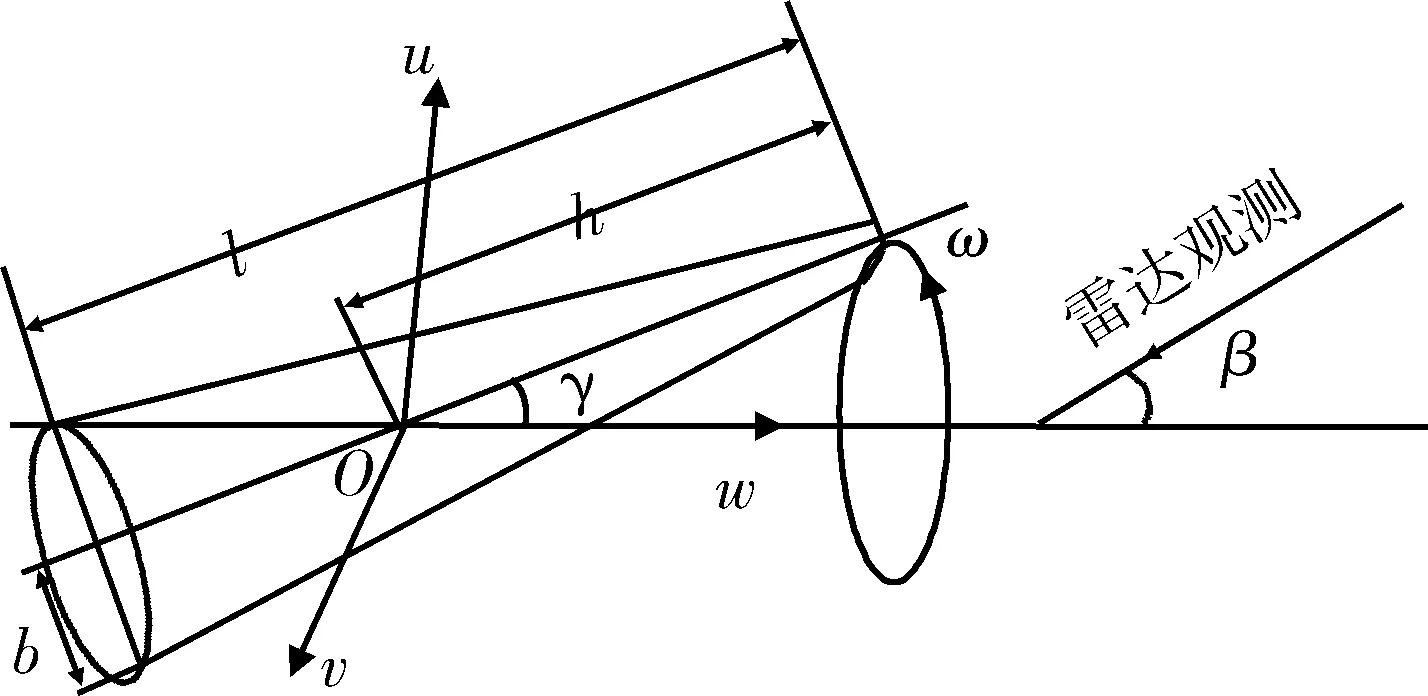
图1 雷达观测固定质心的进动锥体Fig.1 Stationary precession cone in radar sight
建立进动的坐标系Ouvw,设进动轴为w轴,将雷达视线与进动轴组成的平面定义为Ouw面,根据右手螺旋法则确定v轴指向。则进动锥体的对称轴的指向可表示为

(1)
式中:φ0为观测0时刻的进动转角。
雷达视线矢量方向为

(2)
定义雷达视线与锥体对称轴的夹角为雷达视线角,记为α(t),有

(3)
α(t)=arccoscosβcosγ+sinβsinγcos(ωt+φ0).
(4)
由空间几何关系和电磁散射特性的知识可得,锥体有两个强散射中心,分别在球顶和棱边[10],锥体的HRRP长度可表示为
L(t)=lcos(α(t))-bsin(α(t)).
(5)
由式(4),固定质心的进动目标一维距离像的径向长度呈周期性变化,令

(6)
tanη=b/l.
(7)
式(5)可变换为
L(t)=l′cos(η+α(t)).
(8)
则HRRP最小为
Lmin=l′cosβ+γ+η.
(9)
HRRP最大为
Lmax=l′cosβ-γ+η.
(10)
1.2 运动质心的进动目标HRRP径向长度特征
中段飞行的弹道导弹目标,当完成轨道修正和诱饵释放后,控制系统会调整弹头指向保证其最佳再入角,所以在不考虑飞行误差的情况下,可以认为中段飞行的中后期,目标的进动轴在弹道平面内,且指向固定[6]。如图2所示。锥体沿弹道飞行,雷达视线与进动轴夹角是变化的,同时进动也导致了锥体轴指向的改变,上述2种运动共同引起了锥体雷达视线角的改变。
描述飞行的进动锥体雷达视线角随时间的变化,定义2个坐标系,雷达坐标系Oxyz和进动坐标系O′uvw。进动坐标系的定义同前节,设进动轴为O′w轴,并将观测0时刻的雷达视线与进动轴组成平面定义为O′uw面。
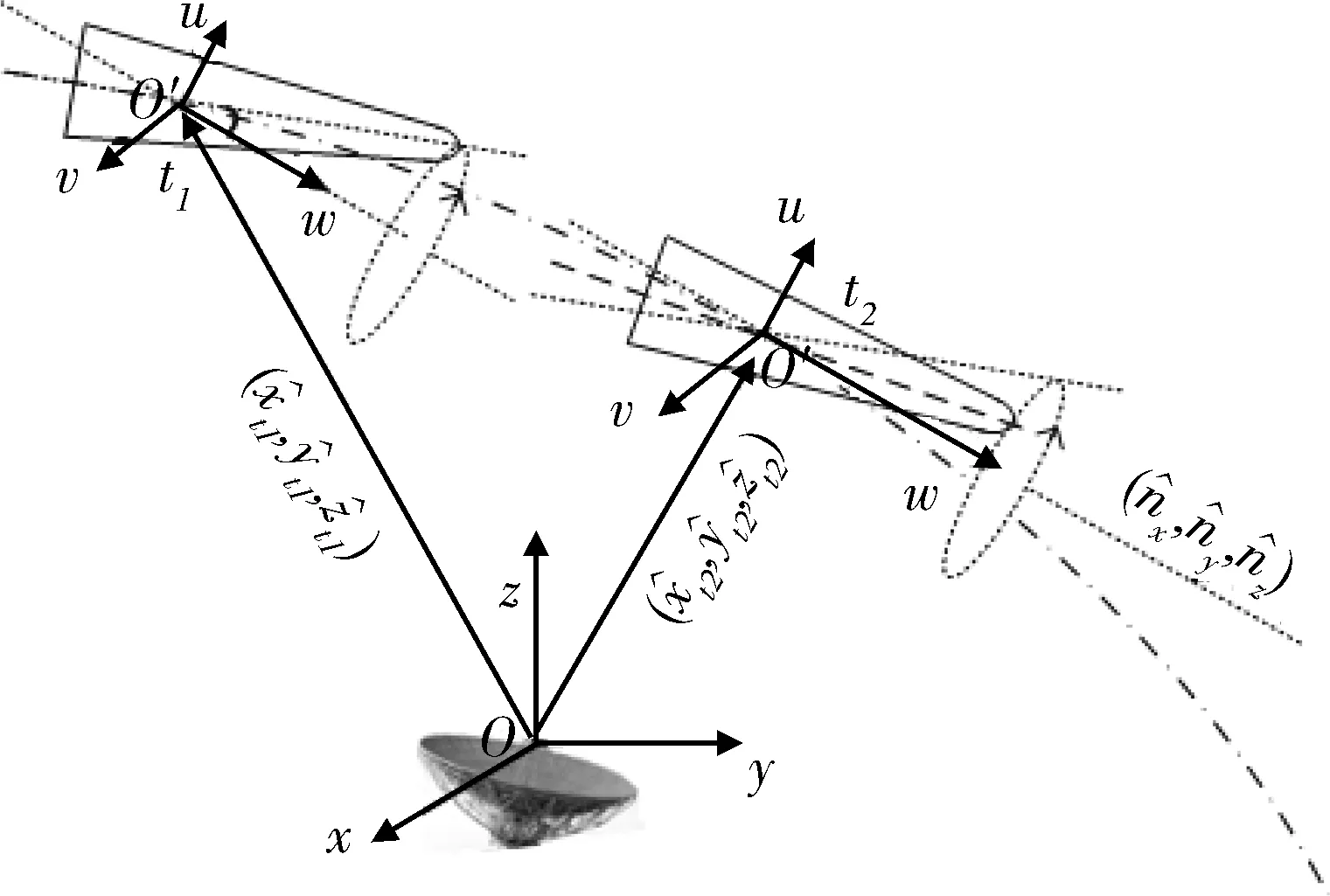
图2 飞行的进动锥体示意图Fig.2 Geometry of flying precession cone
(11)

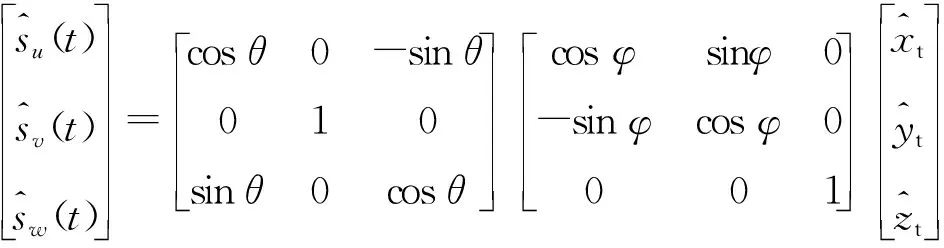
(12)
则进动锥体的对称轴的方向矢量仍可表示为式(1)。将式(12)代入式(3)和(5)即可得到飞行的锥体的HRRP径向长度表达式:
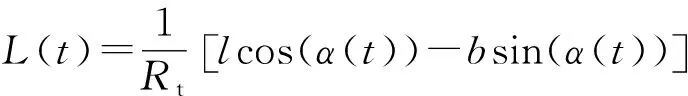
(13)
cos(α(t))=atsinγcos(ωt+φ0)-
btsinγsin(ωt+φ0)+
ctcosγ.
(14)
式中:
(15)
设锥体长度为l=4 m,b=0.5 m,进动角为γ=10°,进动速率ω=2π,进动轴在雷达坐标系中θ=20°,φ=30°,又设飞行锥体的初始质心位置坐标为(x,y,z)=(200,50,200)km匀速飞行速度为(vx,vy,vz)=(-6,0,-4)km/s,并设φ0=0,计算得到HRRP径向长度如图3所示。进动引起HRRP径向长度的起伏,但由于飞行的影响,周期不再是常量,HRRP径向长度的极大值和极小值也随飞行时刻而改变。径向长度随时间的改变为进动参数的估计提供了条件。
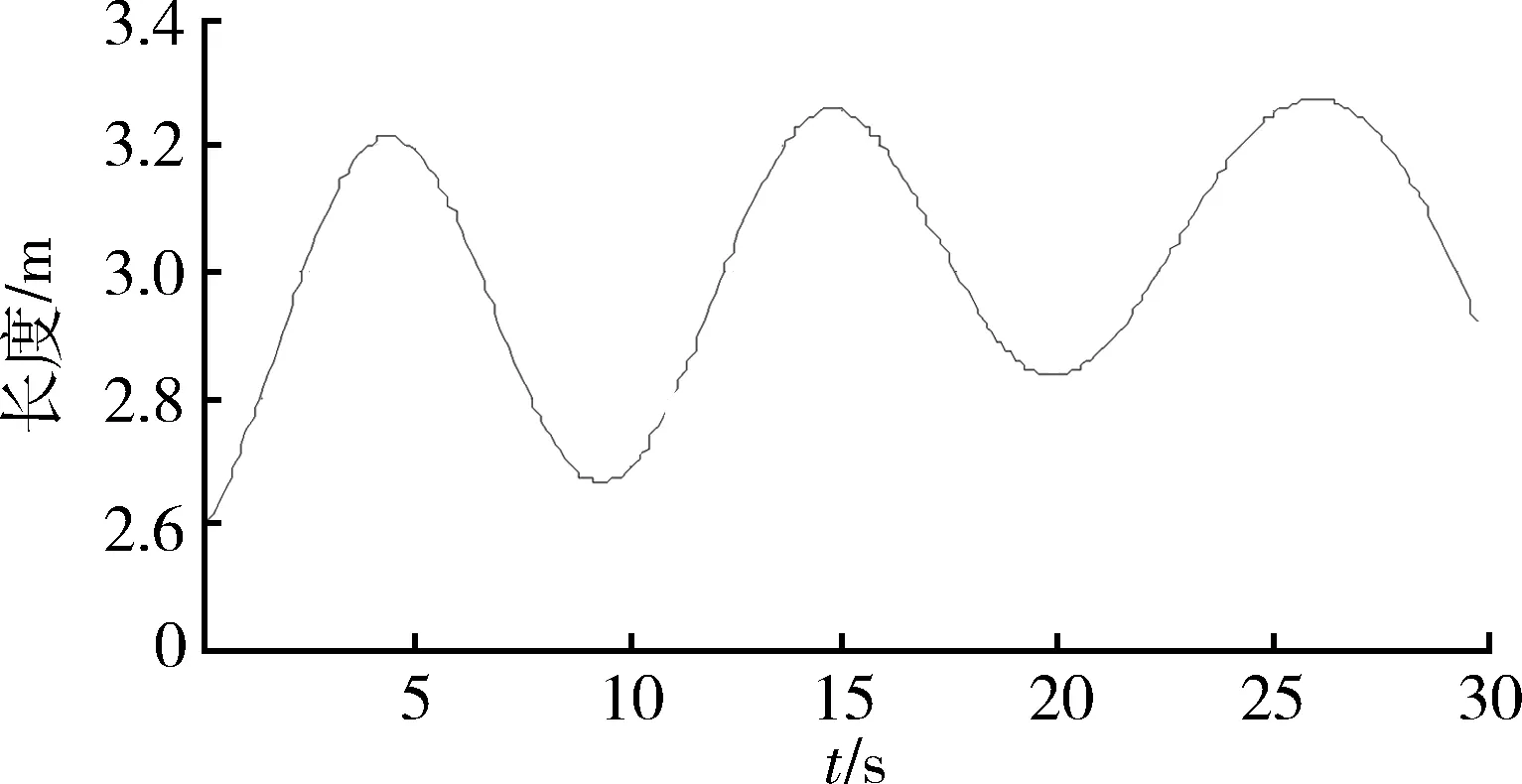
图3 飞行进动锥体的HRRP径向长度Fig.3 HRRP length of flying precession cone
2 飞行进动锥体目标的微动参数估计

min(max)f(x),s.t.x∈S.
(16)
对应于本文的数学模型,最优估计表达式为

(17)
式中:
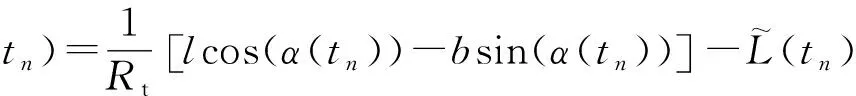
(18)

(19)
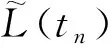
式(18)中有2个三角函数,且未知量多,计算复杂,直接估计困难大。为了提高估计效率,减小计算难度,本文采用分步全局最优估计法:首先将数学模型简化初估,得到未知量的粗估值;再将粗估值作为二次估计的初值,并进一步缩小各参数搜索范围后,利用精确模型再次优化,最终得到的未知量精确解。
模型的简化过程为:对于锥体,当l≫b,且从头部附近观测时有
L(t)≈lcos(α(t)).
(20)
所以可近似简化为

(21)
与原数学模型相比,新模型少了一个未知量,而且方程中只剩一个的三角函数的计算,估计更容易。
利用(21)得到x的初步估计后,根据粗估值,缩小搜索范围,通过精确模型(18)进行二次估计,得到最终结果。为了避免最优解中存在局部最优的问题,一方面根据参数的物理意义,增加约束条件,限制其值域;另一方面可采取变换初值多次估计的方法,以确保结果的准确。
综上,对飞行进动锥体的微动参数估计的具体步骤为:
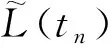
(2) 利用简化的HRRP径向长度模型式(20)对(14)和(15)中的参数粗估计;
(3) 利用参数粗估计的结果,缩小参数的搜索范围;
(4) 利用精确表达式(13)进行二次全局优化,估计得到进动参数的估计值。
3 仿真结果及分析


图4 仿真结果Fig.4 Simulated results
表1 微动参数估计结果Table 1 Estimated results of precession parameters

进动角/(°)进动周期/s圆锥高度/m底面半径/m9.9112.534.010.36
仍利用上述弹道和雷达参数,改变进动角和进动周期,估计的结果如表2所示。
由表2,本文方法能够在不同进动状态下对进动参数进行估计。对进动角、进动周期、圆锥高度的估计效果好,误差均小于10%。其中进动周期的估计准确度最好,对进动角和圆锥高度估计的准确度次之,而对底面半径的估计效果较差。
分析其原因为:由于雷达带宽的限制,HRRP径向长度提取存在误差。径向长度的误差会导致进动参数的误差。该误差对周期参数的影响最小,故对周期的估计效果最好。而根据第2节分析,锥体的底面半径对HRRP径向长度的影响很小,近似可以忽略;所以利用HRRP长度反推底面半径时,精度也不高。

表2 不同参数微动参数估计结果Table 2 Estimated results of several precession parameters
4 结束语
本文提出了一种基于HRRP时间序列和雷达测轨信息的飞行进动锥体目标微动参数的估计方法,能够正确估计进动角、进动周期、锥体高度等参数,上述参数可以作为识别特征量用于目标的分类识别。仿真结果证明了方法的可行性和正确性。该方法可以应用于特征提取和目标识别领域。文中仿真计算未讨论雷达测量误差等不确定因素,在后续工作中还需要进一步研究雷达测量误差和信噪比等对估计精度的影响。
参考文献:
[1] 周万幸. 弹道导弹雷达目标识别技术[M].北京:电子工业出版社,2011.
ZHOU Wan-xing. BMD Radar Target Recongnition Technology[M].Beijing:Publishing House of Electronics Industry, 2011.
[2] CHEN V C, LI Fa-yin, Shen-Shyang Ho, et al.Micro-Doppler Effect in Radar: Phenomenon, Model, and Simulation Study[J]. IEEE , 2006,42(1):2-21.
[3] 李松,冯有前,刘昌云,等. 弹道导弹微动模型及微多普勒特征研究[J]. 现代防御技术,2011,39(6):95-100.
LI Song, FENG You-qian, LIU Chang-yun, et al. Research of Micro-Motion Model and Micro-Doppler of Ballistic Missile[J]. Modern Defence Technology, 2011, 39(6):95-100.
[4] 马梁,王雪松,李永祯,等. 雷达部署对进动目标微多普勒频率的可测性分析[J]. 国防科技大学学报,2011(4):54-59.
MA Liang, WANG Xue-song, LI Yong-zhen, et al. Influence of Radar Location on the Measurability of Micro-doppler Detecting for Precession Target[J]. Journal of National University of Defense Technology, 2011(4): 54-59.
[5] 高红卫,文树梁,谢良贵. 雷达脉冲串波形下的目标微动特征提取[J]. 现代防御技术,2009,37(5),132-135.
GAO Hong-wei, WEN Shu-liang, XIE Liang-gui. Target Micromotion Feature Extraction from Radar Pulse Train Waveform[J]. Modern Defence Technology, 2009, 37(5), 132-135.
[6] 陈行勇,黎湘,郭桂荣,等. 微进动弹道导弹目标雷达特征提取[J]. 电子与信息学报,2006,28(4): 643-646.
CHEN Hang-yong, LI Xiang, GUO Gui-rong, et al. Radar Feature Extraction of Micro-precession Ballistic Missile Warhead[J]. Journal of Electronics & Information Technology, 2006, 28(4): 643-646.
[7] 关永胜,左群声,刘宏伟,等. 空间进动目标微动参数估计方法[J]. 电子与信息学报,2011,33(10):2427-2432.
GUAN Yong-sheng, ZUO Qun-sheng, LIU Hong-wei, et al. Micro-motion Parameters Estimation of Space Precession Targets[J]. Journal of Electronics & Information Technology, 2011, 33(10): 2427-2432.
[8] 贺三思,周建雄,付强,利用一维距离像序列估计弹道中段目标进动参数[J]. 信号处理,2008,25(6): 925-929.
HE San-si, ZHOU Jian-xiong, FU Qiang. Using HRRP Sequence to Estimate the Precession Parameters of Midcourse Target[J]. Signal Processing, 2008, 25(6): 925-929.
[9] 高红卫,谢良贵,文树梁,等. 弹道导弹目标微多普勒特征提取[J].雷达科学与技术,2008,6(2),96-101.
GAO Hong-wei, XIE Liang-gui, WEN Shu-liang, et al. Micro-Doppler Feature Extraction of Ballistic Missile Targets[J]. Radar Science and Technology, 2008, 6(2), 96-101.
[10] 黄培康,殷红成,许小剑. 雷达目标特性[M]. 北京:电子工业出版社,2005.
HUANG Pei-kang, YIN Hong-cheng, XU Xiao-jian. Radar Target Characteristic[M]. Beijing:Publishing House of Electronics Industry,2005.
[11] 彭拯.全局优化的水平值逼近理论与算法研究[D].上海:上海大学,2009.
PENG Zheng. A Study on Theory and Algorithms of Level-Value Approximation to Global Optimization[D].Shanghai: Shanghai University, 2009.
[12] 袁莉,陶巍. 弹道导弹目标的距离像特性与特征分析[J]. 制导与引信,2009,30(2):7-11.
YUAN Li, TAO Wei. Characteristics and Feature Analysis of Range Profile for Ballistic Missile Target[J]. Guidance & Fuze, 2009, 30(2): 7-11.
[13] 温晓杨,卢大威,张军. 快时间域微振动对高分辨距离像畸变分析[J]. 现代防御技术,2010,38(6):126-131.
WEN Xiao-yang, LU Da-wei, ZHANG Jun. HRRP Distortion Analysis of Vibration Scatters in Fast Time Domain[J]. Modern Defence Technology, 2010, 38(6), 126-131.
[14] 徐庆,王秀春,李青. 基于高分辨一维像的目标特征提取方法[J]. 现代雷达,2009,31(6):60-63.
XU Qing, WANG Xiu-chun, LI Qing. Extraction of Target Feature Using High Resolution Range Profile[J]. Modern Radar, 2009, 31(6): 60-63.

