基于Marichal熵和Choquet模糊积分的BVR防空作战TA研究

孙永芹，纪金耀，马兴华，姚成柱

(1.中国人民解放军91206部队，山东 青岛 266108；2.海军潜艇学院，山东 青岛 266071)

0 引言

随着高新防空武器的服役，其作战范围达到了前所未有的广大空间。同时，远程精确制导技术的发展，使空中打击行动不仅可进行临空轰炸，还可随行非接触式空袭，这些变化促使超视距(beyond-visual-range, BVR，飞行员目力范围以外，约10 km以上)、“攻防兼备”型新概念防空成为现代防空的第一选择。在现代防空作战中，面对大规模的各类目标，对目标威胁进行科学、准确地评估，是避免重复攻击、提高作战效能的关键因素，具有重要的研究价值和实战意义。

1 威胁评估方法概述

威胁评估(threat assessment, TA)问题的研究，2000年左右已有文献报道，近年来已被激活，各种方法相互融合和改进，取得了一些成绩[1-10]，如协调优势粗糙集方法[6]、马尔可夫链[7,11]、Vague物元[8,12]等TA参量法，以及一些改进的TA非参量法[10]。但这些方法大多参考了近距作战的TA模型，如文献[9-10]等，不适用于BVR作战的TA。文献[13]提出了一种超视距空战TA非参量法模型，但该方法所使用的模型较为粗糙，且构造的进入角、方位角优势函数不符合实际情况。而且在BVR防空作战中，威胁因素之间往往具有一定的相关性，如何有效地表示相关因素的重要性，并对其进行综合，将直接影响TA的结果。因此，本文引入模糊测度与模糊积分理论，解决上述TA问题，提出一种适用于BVR防空作战的TA方法。TA问题实际上是根据威胁因素确定目标威胁等级的过程：①选取影响TA的威胁因素;②确定各属性的重要性；③采用一定的集成算法对各因素的影响进行综合，实现目标TA。本文综合考虑敌我双方战机(包括其武器)性能，从整个体系做出分析，选取来自空战态势、效能、对双方做出威胁行为的事件、目标战役价值为主要影响TA的因素，建立BVR防空作战TA优势函数模型，采用Marichal熵算法确定各威胁因素的模糊测度，然后采用Choquet模糊积分对各因素的影响进行综合，实现TA。如图1所示。

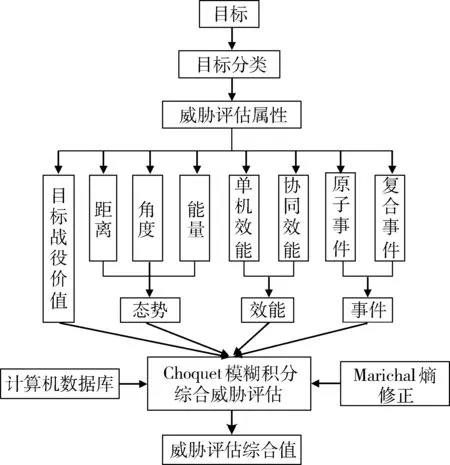
图1 威胁评估框图Fig.1 Flow chart for threat assessment

2 BVR防空作战威胁评估因素优势函数建模

2.1 态势优势模型

假定BVR防空作战中作战态势如图2所示，L为作战双方之间的距离，φ是目标方位角，q是目标进入角，且0≤|q|≤180°，0≤|φ|≤180°。v是我方速度，vt是目标速度。

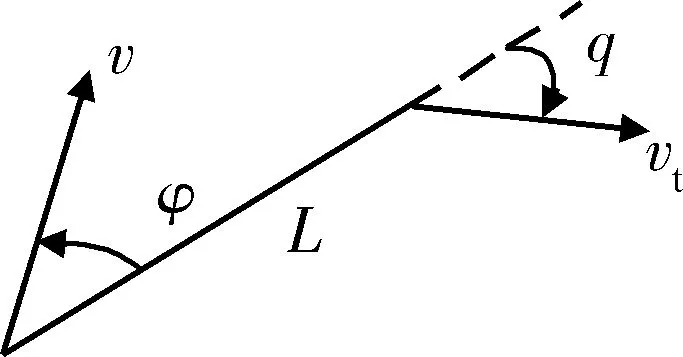
图2 双方作战态势图Fig.2 Combat situation of both sides

2.1.1 距离优势函数

现代战机空战能力除与飞机性能(如机头快速指向能力)有关外，主要取决于火控雷达和空空导弹的性能[13-16]。距离指标是决定火控雷达性能和空空导弹性能的主要指标之一，其具体包括雷达最大搜索距离Lrmax、导弹最大攻击距离Lmmax、导弹不可逃逸区最大距离Lmk max、导弹不可逃逸区最小距离Lmk min。因此，距离对优势指数的影响可以认为主要反映在雷达发现概率和导弹的杀伤概率上。对于一定雷达反射截面积的目标，雷达发现概率随距离增大而减小，且在L≥Lrmax时，虽然不能依靠自身探测设备发射武器，但可以借助其他平台传送的目标信息，装订目标参数，发射远程攻击武器。故而构造如下距离优势函数：

(1)

2.1.2 角度优势函数

角度指标是决定火控雷达性能和空空导弹性能的另一个主要指标，其具体包括雷达最大搜索方位角φrmax，空空导弹最大离轴发射角φmmax，不可逃逸区圆锥角φmk max。

随着“离轴发射”等先进火控技术的发展，使得作战飞机在机头在不指向目标的情况下也可以进行攻击，而且进入角对优势函数也是有影响的，主要体现在对导弹杀伤概率的影响上[13-16]。另外，在双方迎头作战和尾追条件下，进入角的优势是不同的，一般说来，双方迎头作战时，可以在较远距离发射中远距空空导弹，优势较大，尾追条件下优势较小。故而构造进入角优势函数：

(2)

方位角对优势指数的影响主要反映在雷达发现概率和导弹的杀伤概率上。当目标进入雷达搜索区，但未进入导弹攻击区，此时优势较小；进入导弹攻击区而未进入不可逃避区，此时优势居中；目标进入不可逃避区，若距离也小于一定值，则无论目标作何机动，此时发射导弹，都将以不低于一定的杀伤概率值杀伤目标；在雷达搜索区以外的区域，方位角优势函数值相对较小，但是不能简单的等于0，且不同的方位角度下，其方位角优势是不同的。故而，构造方位角优势函数：

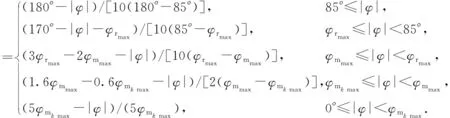
(3)

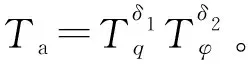
2.1.3 能量优势函数

在BVR防空作战中，载机高度和速度对导弹射程都是有影响的[17]，从而影响总体优势。所以，不考虑高度对优势函数的影响是不合理的。因此，定义战机单位能量为E=H+v2/2g，参阅文献[17]的能量优势函数，构造战机能量优势函数为

(4)

式中：E为战机单位能量；Et为目标机单位能量；g为当地重力加速度。

2.1.4 态势优势函数

假设β1，β2，β3分别为战机相对于目标机的角度优势、距离优势、能量优势的权值，且β1+β2+β3=1(0≤β1,β2,β3≤1)。综合角度优势、距离优势、能量优势，即可得到态势优势：

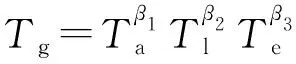
(5)

2.2 效能优势模型

空战能力指数C，本文取参考文献[18]中的定义，计算所得数据保存在数据库中，依据敌我双方装备变更情况适时更新。该空战能力指数很全面的反映了各种类型飞机的静态作战能力。但在BVR防空作战中，数据链成员共享信息，之间相互协同作战，只考虑敌机的空战能力的单机效能优势函数是不全面的，甚至有可能对作战效果造成不利的影响。故而，构造效能优势如下：

首先将空战能力指数进行归一化处理，这里取空战能力指数的相对值TCi，设i是第i架飞机，则

TCi=Ci/maxCi.

(6)

设TCa，TCt分别为归一化后的战机与目标机的空战能力指数，构造效能优势：

Tm=TCa-TCt+1/2.

(7)

2.3 事件优势模型

作战实体在作战过程中会不断出现加(减)速、拐弯、爬升、辐射源开(关)机、导弹符合发射条件等属性变化行为，这些行为都可能对对方作战实体产生威胁，这些产生威胁的行为即事件。本文简单选取以下几个具备代表性的相关事件，定义如下事件优势TI。

(1) 实体雷达辐射：未辐射时，TI=0；对目标机扫描时，TI=0.5；对目标机进行多目标跟踪时，TI=0.8；对目标机连续跟踪时，TI=1。

(2) 实体导弹发射：对目标机发射导弹时，TI=1。

2.4 目标战役价值对威胁评估的影响

在BVR防空作战中，除了考虑敌机群对我机(群)的威胁，还要将其对我要保护的目标的威胁(表现为目标的战役价值)考虑在内。目标的战役价值J一般由作战指挥系统确定，也可以根据目标的对地攻击能力或者特种作战能力(预警、电子干扰等)确定，其具体的计算取值参阅文献[18]。需要说明的是，为了和其他因素的数量级一致，一般J乘以0.1，用TJ表示，即为TJ=0.1J。

3 Marichal熵确定各威胁因素的重要性

3.1 模糊测度

模糊测度是日本学者Sugeno在1974年首次提出的，它是对因素集的建模，可以表示一个或多个指标的综合重要程度，更加准确地刻画了多个指标之间的相互关系[9]。其定义如下：设(X,F)为一可测空间，F为X的所有子集组成的σ-代数，g是F上的一个模糊测度，如果存在λ>-1，∀A,B⊆X,A∩B=Φ，满足：

gA∪B=gA+gB+λgAgB.

(8)

则称g为gλ模糊测度。若X={x1,x2,…,xn}为有限集合，则映射：xi→gi=g({xi})，i=1,2,…,n，称为模糊密度函数。gλ模糊测度可完全由其模糊密度函数确定，即

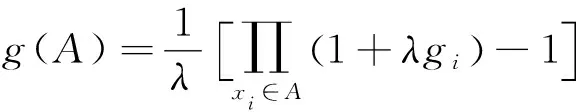
(9)

态势、效能、事件、目标战役价值等威胁因素，相互之间并不孤立，故而本文采用模糊测度表示各优势函数的重要程度。

3.2 Marichal熵计算威胁因素的模糊测度

Marichal熵算法是一种常用的计算模糊测度的方法[9]，它通过数据学习得到模糊测度，比较客观，其具体计算思路是：采用Marichal熵构建目标函数，建立优化模型，通过最大化Marichal熵求解各优势函数的重要程度。

模糊测度Marichal熵的定义为

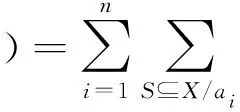
(10)

式中：X为因素集；n为X中元素个数；gλ为定义在X上的模糊测度；ξS(n)和μ(x)分别为

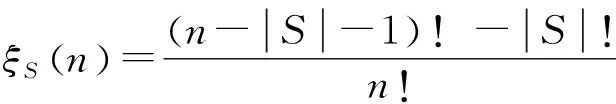
(11)

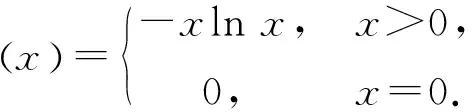
(12)

依据优化模型式(13)求解威胁因素各优势函数的模糊测度：

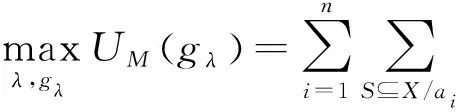
(13)

式中：Ii为单个因素的Shapley值，表示因素的全局重要性，可通过采用适当的方法(如层次分析法)得到。

4 Choquet模糊积分确定威胁排序

综合态势、效能、事件、目标战役价值等威胁因素的集成算法，即相关因素的集结算子，采用模糊积分，模糊积分的形式有很多，本文采用Choquet模糊积分，其定义如下：

设有限集合X={x1,x2,…,xn}，函数f为离散值函数，函数值分别为{f(x1),f(x2),…,f(xn)}，且假设f(x1)≤f(x2)≤…≤f(xn)，则f在X上关于测度ρ的Choquet模糊积分定义[9]为

(14)

式中：f(x0)=0；Ai={xi,xi+1,…,xn}。

Choquet积分是对加权平均算子的扩展。

采用上述的Choquet模糊积分综合各优势函数，可得防空作战总体优势函数T，由此可得目标的优势排序，最终的威胁排序即是该优势排序的反序列。

5 仿真验证与分析

针对目标进入角、方位角、双方相对距离、高度、速度、效能、事件变化对总体优势函数T的影响进行了仿真，仿真数据为：φrmax=65°，φmmax=35°，φmk max=20°；Lrmax=140 km，Lmmax=80 km，Lmk max=60 km，Lmk min=40 km；由专家判断所得Shapley值，如表1所示，图3～9分别为总体优势函数T随不同参数的变化图；执行要地防空任务时，专家判断所得Shapley值如表2所示，图10是总体优势函数T随目标机的目标战役价值的变化图。

针对Marichal熵和Choquet模糊积分解决威胁评估相关性问题进行仿真，假设防空战中有8架目标机，其型号分别是F-16C，F-15E，F-5E，作战态势如表3所示。8架目标机的相关参数、目标属性值及战役价值如表4所示，Shapley值如表2所示。由本文所建模型得到8架敌机的总体优势函数值，如表5所示。

表1 威胁因素的Shapley值Table 1 Shapley values for threat factor

表2 执行要地防空任务时，威胁因素的Shapley值Table 2 Shapley values for threat factor in air defense combat

表3 双方作战态势表Table 3 Combat situation of both sides

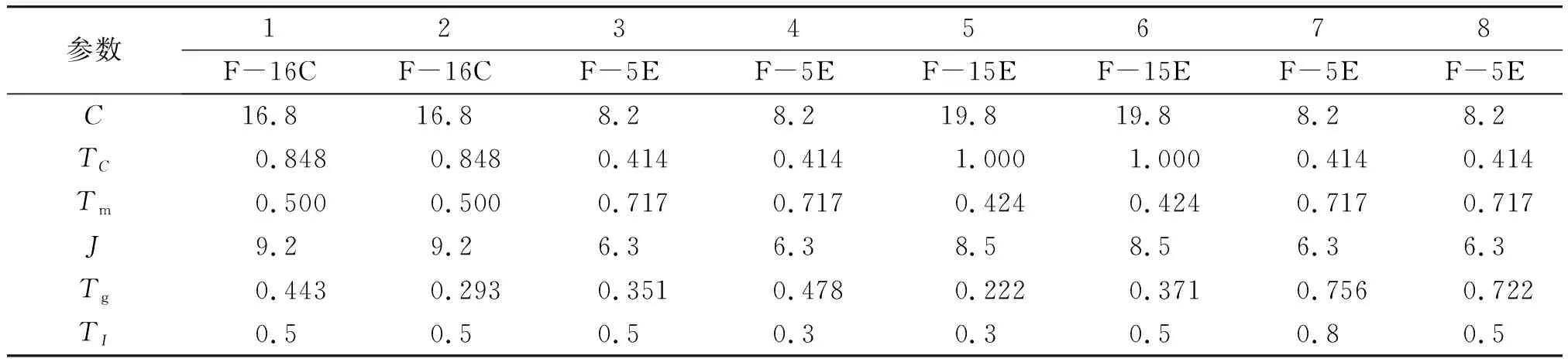
表4 8架目标机的相关参数、目标属性值及战役价值表Table 4 Correlation parameters, attribute values, goal campaign value for 8 targets

表5 8架目标机的总体优势函数值表Table 5 Values of total advantage function for 8 targets

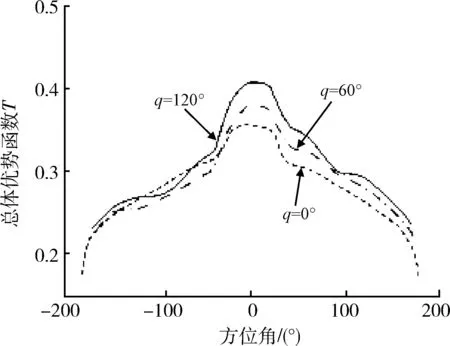
图3 总体优势函数随方位角变化图Fig.3 Total advantage function changes with azimuth

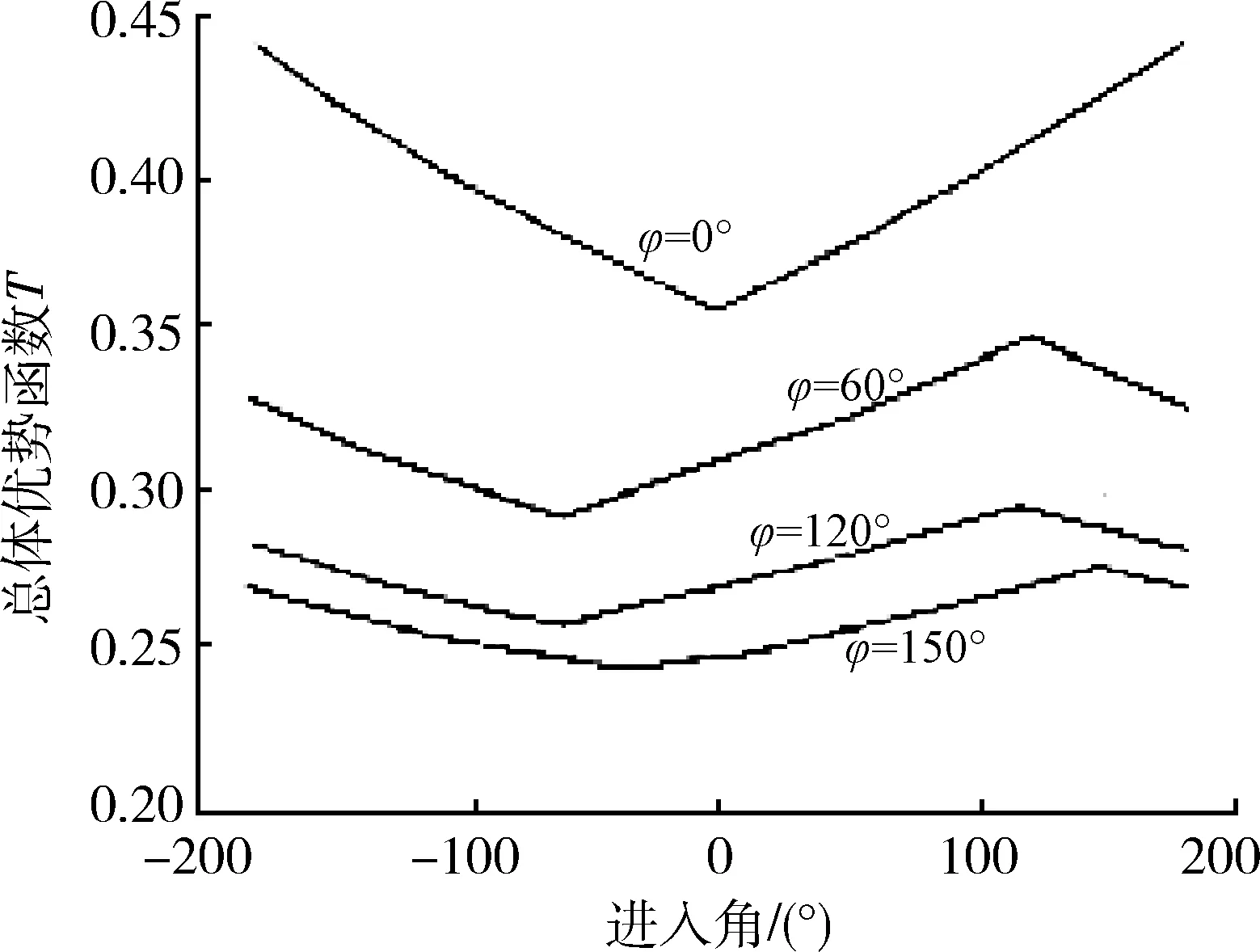
图4 总体优势函数随进入角变化图Fig.4 Total advantage function changes with enter angle

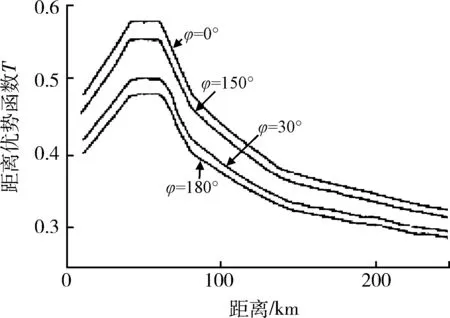
图5 总体优势函数随距离变化图Fig.5 Total advantage function changes with distance

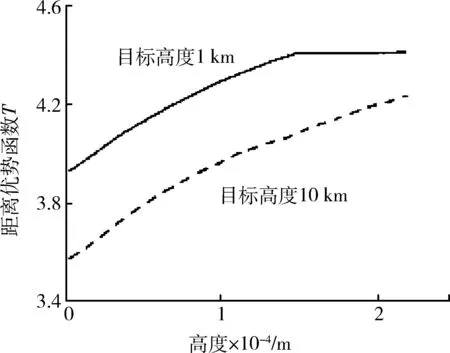
图6 总体优势函数随高度变化图Fig.6 Total advantage function changes with height

图7 总体优势函数随速度变化图Fig.7 Total advantage function changes with speed

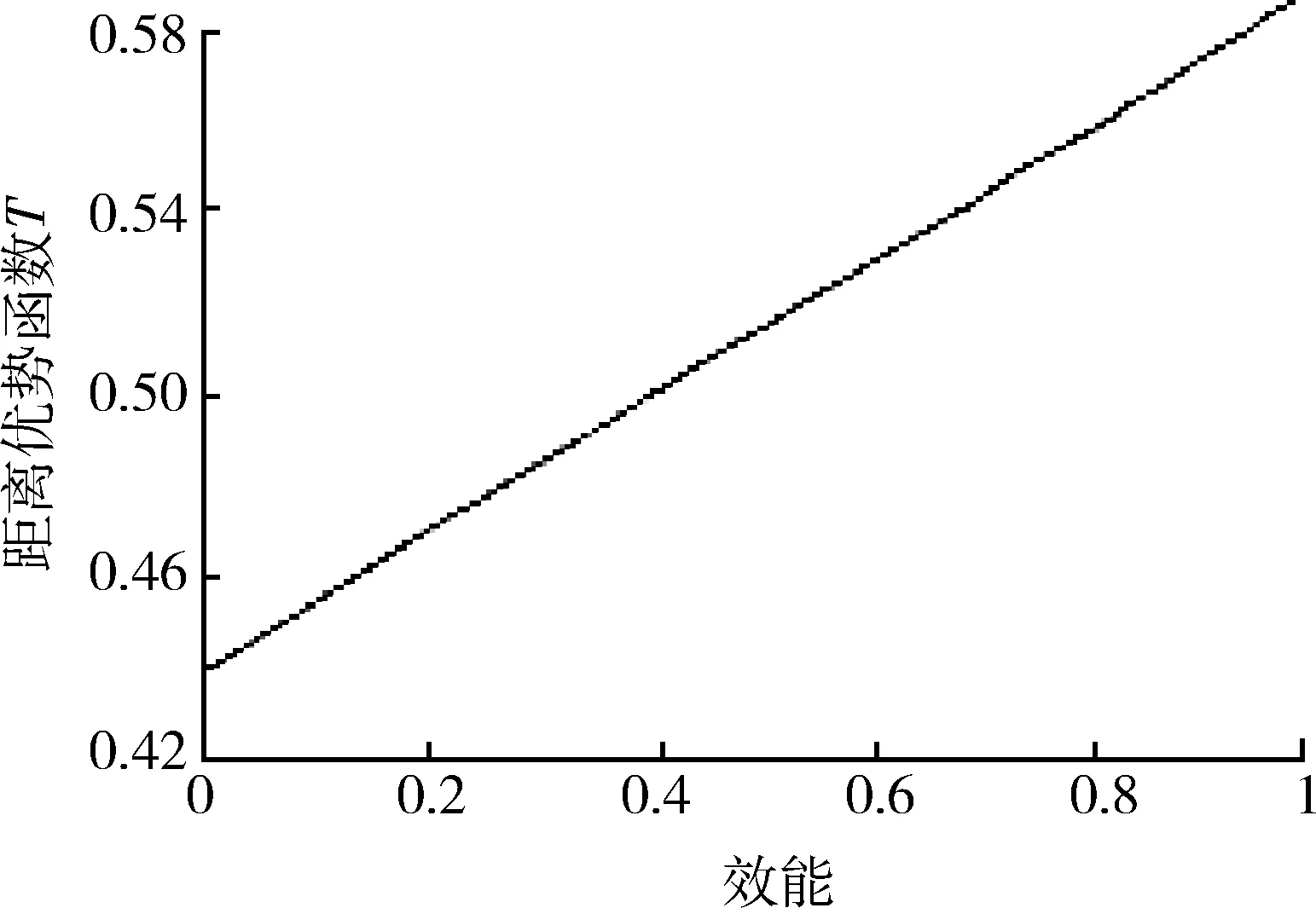
图8 总体优势函数随空战效能变化图Fig.8 Total advantage function changes with efficiency

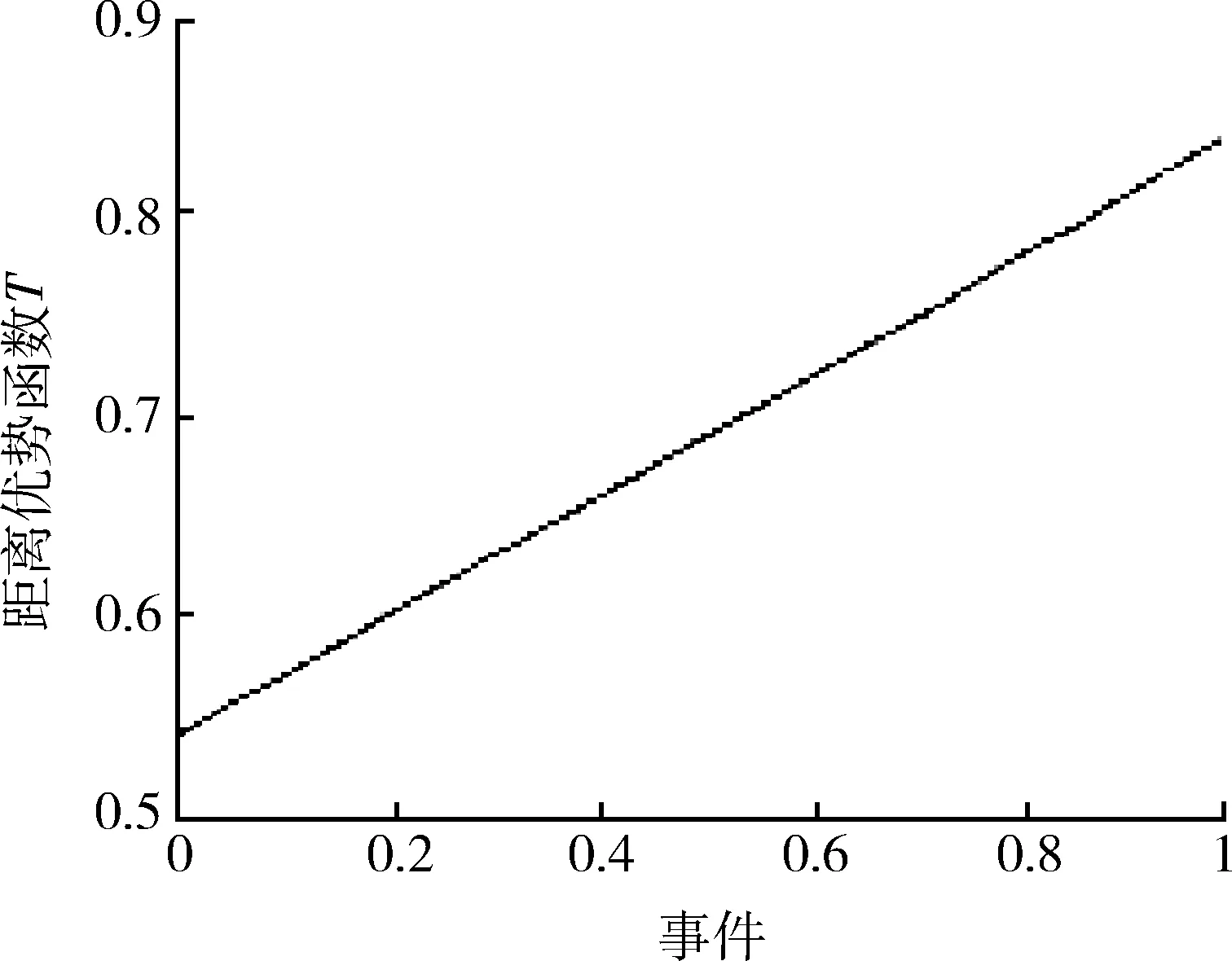
图9 总体优势函数随事件变化图Fig.9 Total advantage function changes with event

图10 总体优势函数随目标战役价值变化图Fig.10 Total advantage function changes with goal campaign value

由图3可得，在不同的进入角下，相同的方位角对应的总体优势不一样。由图4可得，在不同的方位角下，相同的进入角对应的总体优势也不一样。图5反映了目标在导弹不可逃逸区内时总体优势最大。图6～10分别反映了总体优势随战机高度、战机速度、效能优势、事件优势、目标战役价值的增大而增大。故而，所建优势函数模型合理、可行，符合BVR防空作战规律。

由表3得8架目标机的优势排序为(由大到小)：(1，2，7，6，8，5，3，4)。故而最终的威胁排序为(由大到小)：(4，3，5，8，6，7，2，1)。所以，Marichal熵算法和Choquet模糊积分可有效解决TA中威胁因素关联问题，实现威胁排序。

6 结束语

本文针对BVR防空作战，建立了TA优势函数模型，优化了态势优势、效能优势，增加了目标战役价值；并针对威胁因素之间常存在关联的情况，引入模糊测度和模糊积分，提出了基于Marichal熵和Choquet模糊积分的TA方法，用gλ模糊测度对关联TA因素的重要程度进行建模，专家判断提供了Shapley值，Marichal熵算法计算了gλ；模糊测度；Choquet积分实现了威胁排序。最后进行了仿真分析，仿真结果表明所建立的模型合理、可行。

参考文献：

[1] CHEN Jun, YU Guan-hua, GAO Xiao-guang. Cooperative Threat Assessment of Multi-Aircrafts Based on Synthetic Fuzzy Cognitive Map[J]. J. Shanghai Jiaotong Univ. (Sci.), 2012,17(2): 228-232.

[2] 文云峰,石章松,吴彬,等.舰艇自防御的威胁排序方法研究[J].现代防御技术，2012,40(2):77-81.

WEN Yun-feng, SHI Zhang-song, WU Bin, et al. Research on Threat Sequencing of Ship Self-Defense[J]. Modern Defense Technology，2012,40(2):77-81.

[3] 王改革,郭立红,段红,等.基于Elman-AdaBoost强预测器的目标威胁评估模型及算法[J]. 电子学报，2012,40(5):901-906.

WANG Gai-ge,GUO Li-hong,DUAN Hong, et al. The Model and Algorithm for the Target Threat Assessment Based on Elman-AdaBoost Strong Predictor[J]. Acta Electronica Sinica，2012,40(5): 901-906.

[4] 陈华,张可,曹建蜀.基于PSO-BP算法的目标威胁评估[J].计算机应用研究，2012,29(3):900-901,932.

CHEN Hua, ZHANG Ke, CAO Jian-shu. Target Threat Assessment Based on PSO-BP Algorithm[J]. Application Research of Computers，2012,29(3):900-901,932.

[5] 周玉龙,何永强,张维安.红外鱼眼系统下的多目标威胁评估研究[J].光学学报.2012,32(6):1-6.

ZHOU Yu-long, HE Yong-qiang, ZHANG Wei-an. Multi-Target Threat Assessment of the Infrared Fisheye System[J]. Acta Optica Sinica,2012,32(6):1-6.

[6] 蔡佳,胡杰,黄长强.协调优势粗糙集方法及其在UCAV目标威胁估计中的应用[J].系统工程理论与实践,2012,32(6):1377-1384.

CAI Jia, HU Jie, HUANG Chang-qiang. A Consistent Dominance Rough Sets Method and Its Application in Threat Assessment of UCAV′s Targets[J]. Systems engineering Theory & Practice,2012,32(6):1377-1384.

[7] 韩占朋,王玉惠,姜长生,等.基于马尔可夫链的新型威胁评估预测方法[J].吉林大学学报：信息科学版,2012,30(2):151-156.

HAN Zhan-peng, WANG Yu-hui, JIANG Chang-sheng, et al. New Threat Assessment Prediction Method Based on Markov Chain[J]. Journal of Jilin University：Information Science ed,2012,30(2):151-156.

[8] 夏璐,邢清华,范海雄.Vague物元及熵权的空袭目标威胁评估[J].火力与指挥控制,2012,37(2):84-88.

XIA Lu, XING Qing-hua, FAN Hai-xiong. Threat Evaluation of Air Attack Targets Based on Vague Matter-Element and Entropy Weight[J]. Fire Control & Command Control,2012,37(2):84-88.

[9] 黄洁,李弼程,赵拥军.基于Choquet模糊积分的目标威胁评估方法[J].信息工程大学学报，2012,13(1):18-21.

HUANG Jie, LI Bi-cheng, ZHAO Yong-jun. Target Threat Assessment Based on Choquet Fuzzy Integral[J]. Journal of Information Engineering University，2012,13(1):18-21.

[10] 谷向东,童中翔,郭辉,等.IAHP和熵权相结合的TOPSIS法的空战目标威胁评估[J].火力与指挥控制，2012,37(1):69-72.

GU Xiang-dong, TONG Zhong-xiang, GUO Hui, et al. Target Threat Assessment for Air Combat Based on TOPSIS Combining by IAHP and Entropy Weight[J].Fire Control&Command Control，2012,37(1):69-72.

[11] WU Yan, WANG Xin, XIAO Ping, et al. Fast Algorithm Based on Triplet Markov Fields for Unsupervised Multi-class Segmentation of SAR Images[J]. SCIENCE CHINA, 2011,54(7):15244-1533.

[12] JUN Y. Using an Improved Measure Function of Vague sets for Multi-Criteria Fuzzy Decision-Making[J].Expert Systems with Applications,2010,37(9):4706-4709.

[13] 高永,向锦武.一种新的超视距空战威胁估计非参量法模型[J].系统仿真学报，2006,18(9):2570-2573.

GAO Yong, XIANG Jin-wu. New Threat Assessment Non-Parameter Model in Beyond-Visual-Range Air Combat[J]. Journal of System Simulation，2006,18(9):2570-2573.

[14] WANG Na, WANG Guo-hong, ZENG Jia-you, et al. Range Ambiguity Resolving of HPRF Radar Based on Hybrid Filter[J]. Science China, 2011,54(7):1534-1546.

[15] HAN RUSNAK. Bouunds on the Root-Mean-Square Miss of Radar-Guided Missiles Against Sinusoidal Target Maneuvers[J].Journal of Guidance ,Control, and Dynamics,2011,34(4):1060-1069.

[16] Graham V Weinberg. An Investigation of the Pareto Distribution as a Model for High Grazing Angle Clutter, ADA543170[R].Australia,2011.

[17] 马伟江,姚佩阳,冯煊,等.基于多级模糊综合评判法的态势评估方法研究[J].电光与控制,2011,18(62):21-25.

MA Wei-jiang, YAO Pei-yang, FENG Xuan, et al. Research on Situation Assessment Based on Multi-Level Fuzzy Integration Judgment[J]. Electronics Optics & Control,2011,18(62):21-25.

[18] 朱宝鎏,朱荣昌,熊笑非.作战飞机效能评估[M].北京:航空工业出版社,2006:63-68.

ZHU Bao-liu, ZHU Rong-chang, XIONG Xiao-fei. Effectiveness Evaluation of Combat Aircraft[M].Beijing: Aeronautics Industry Press,2006:63-68.