基于角加速度反馈的自抗扰过载控制系统设计

史静宇,沈 凯,胡宇晖,钟 鼎

（1.北京理工大学,北京 100081; 2.莫斯科国立鲍曼技术大学,莫斯科 105005）

0 引言

21世纪以来,随着新一轮科技革命与产业变革向纵深推进,信息化、智能化装备（特别是高动态飞行器等）加速演进,逐渐呈现出信息获取高维化、扰动抑制主动化、运动控制精准化等特点。高动态飞行器的飞行环境复杂、包线跨度大、气动特性变化,大空域、长距离的复杂飞行环境会给控制系统带来诸多不确定扰动影响,表现为强非线性、强耦合、快时变、不确定、静不稳定和非最小相位等特点[1-2],强控制输入约束条件下难以保证姿态高精度稳定控制。

本文采用过载控制技术,通过各类传感器件直接测量和控制过载状态量来操纵高动态飞行器的飞行,以达到期望的运动轨迹。与传统的姿态控制方案相比,过载控制无需测量纵向和航向上的姿态角和角速率,因而可以不使用陀螺仪,这降低了驾驶仪的制造成本,并简化了其结构[3-4]。针对大空域、宽速域等复杂飞行条件下快速精准控制需求,本文创新提出了基于角加速度直接测量的反馈控制方案,以线加速度计和角加速度计作为组合传感器件构成双回路过载自动驾驶仪,具有结构简单、安装方便、成本低廉、工作可靠的特点[5]。同时,与角速度反馈相比,角加速度反馈具有更好的控制效果和稳定性。

随着高动态飞行器速度和机动性的不断提高,传统PID 控制往往难以获得良好的控制效果[6],自抗扰控制（ADRC）技术的应用为提高高动态飞行器控制系统在干扰条件下的控制效果提供了一种新的思路[7-9]。本文在传统控制系统的基础上采用自抗扰控制技术,针对高动态飞行器的非线性模型,将系统中的耦合干扰、气动参数变化及机体结构偏差等不确定因素通过扩张状态观测器进行观测、估计和补偿,从而获得理想的闭环动态性能[10-11]。在设计方面,自抗扰控制系统可以忽略系统中非线性干扰因素,简化了设计过程,更便于工程实现;在控制效果方面,消除了传统的“前馈+PID” 控制方案的响应速度慢、抗干扰能力弱的缺点,能够获得更高的控制精度。

本文的主要工作有: 1）提出了基于角加速度反馈的自抗扰过载控制方法,分析对比了采用PID 和ADRC 等不同控制算法的自动驾驶仪控制性能;2）分析了采用自抗扰控制算法的自动驾驶仪稳定性,得到其等效闭环传递函数,并采用频域法分析角速度和角加速度反馈控制的系统性能;3）通过数值仿真分析对比了两回路自动驾驶仪在不同反馈回路、不同控制算法、不同静稳定特性下的频域特性。实验结果表明: 基于角加速度反馈的自抗扰过载控制系统具有更优良的控制效果,显著提升了系统的跟踪性能、稳定性和鲁棒性。

1 高动态飞行器过载控制系统模型

1.1 高动态飞行器运动模型

高动态飞行器在弹体坐标系和速度坐标系中的运动模型如图1所示。本节首先建立高动态飞行器的运动学和动力学模型,为过载控制系统设计提供模型基础。

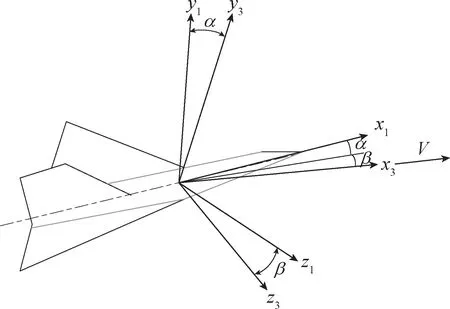
图1 高动态飞行器的机体坐标系和速度坐标系Fig.1 Body coordinate system and velocity coordinate system of high dynamic aircraft

对于高动态飞行器,纵向通道的设计较为典型,且对于航向等其他通道具有参考意义,因此为方便研究,只以其纵向平面运动为例进行分析。高动态飞行器纵向运动的方程组如下

式（1）中,α为攻角,ϑ为俯仰角,θ为弹道倾角,v为飞行速度,x、y为质心位置坐标,Jz为转动惯量,Mz为作用力矩,P为发动机推力,X、Y为气动力,ωz为角加速度,mc为飞行器质量每秒消耗数。

当采用小扰动、线性化和系数冻结法后,可得到简化的飞行器纵向运动方程组[12]

式（2）中,δz为升降舵控制偏角信号;aω为阻尼动力系数;aδ为操纵动力系数;bα为法向动力系数;bδ为舵面动力系数;aα为恢复动力系数,与静稳定度相关: 当aα>0 时系统处于静稳定状态,当aα=0 时系统处于静中立状态,当aα<0 时系统处于静不稳定状态。

由式（2） 可得纵向平面俯仰运动的机体传递函数

式（3）中,Km为传递系数,Tc为时间常数,ξc为相对阻尼系数,均为同机体特征相关的系数,并由下式计算得到

将式（3）中增量符号略去,转化为微分式得

式（7）两边取拉普拉斯变换,可得到对应的过载二阶传递函数

1.2 高动态飞行器过载控制方法

高过载飞行器的过载控制是指通过直接测量和控制机体横向过载及其变化率,以操纵其飞行轨迹并按照预定的弹道飞行。飞行器的过载矢量可以表征改变机体飞行速度大小和方向的能力,因此可以用来直接反映其机动能力[13]。理论上,高过载飞行器的可用过载越大,其机动性能就越好,所以过载控制方法对高过载飞行器末端机动有较好的控制能力。

在小攻角和小侧滑角的条件下,可得到在机体坐标系中机体横向过载ny（nz） 与外加作用力的关系

式（9）中,Y1、Z1分别为升力和侧向力,mg为重力。

因此,可以通过测量和控制机体的过载来控制其外作用力。对于轴对称结构的高动态飞行器来说,在机体坐标系上有

由式（10）可知,角加速度与控制飞行器的作用力矩成正比关系。因此,可以通过测量和控制机体的角加速度来控制飞行器的外作用力。

飞行器的俯仰角ϑ与弹道倾角θ之间的关系为

式（11） 中,τ为时间常数。忽略通道间耦合,式（11）可改写为

在纵向通道上,由式（1）近似可得

则有

将式（14）代入式（1）得到

由此可见,横向过载的一阶微分可视为角加速度与一阶惯性环节串联。为简化计算,常将式（15）中的一阶惯性环节简化为比例环节

式（16）表明可以用角加速度来近似表示机体横向过载变化率,因此可利用角加速度计（或陀螺仪）直接对角加速度（或角速度）测量来控制飞行器横向过载及其变化率,从而实现过载控制。

1.3 自动驾驶仪控制回路设计

针对自动驾驶仪控制回路设计问题,建立过载控制系统的两种带PI 校正的典型模型,其均以线加速度计的测量值作为主反馈,并分别采用陀螺仪和角加速度计作为阻尼回路,以改善机体的等效阻尼[4]。

（1）基于角速度测量的自动驾驶仪控制回路

角速度制导回路的典型结构如图2所示。图2中,ωz/δz可根据式（8）、式（15）得到

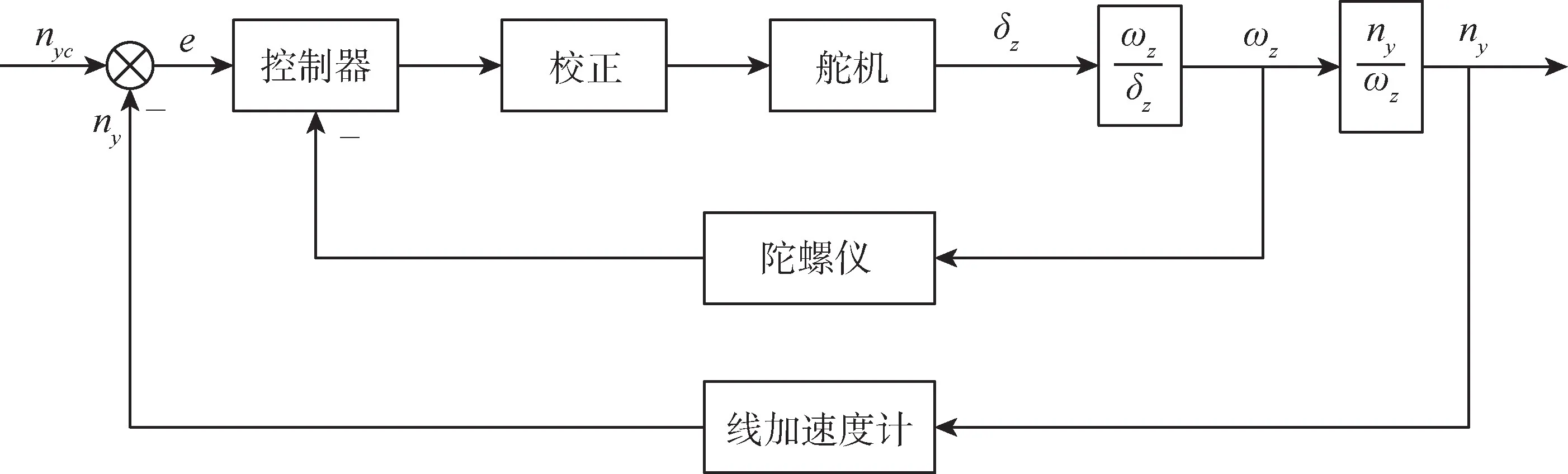
图2 角速度控制回路Fig.2 Diagram of angular velocity control loop

该控制系统的输入为横向过载指令nyc,且包含有内、外两个反馈回路: 反馈内环用于稳定自动驾驶仪控制回路姿态运动,其中的角速度信号ωz由陀螺仪测得;反馈外环实现对过载指令的跟踪,其横向过载ny由线加速度计测得。

（2）基于角加速度直接测量的控制回路

与角速度回路相比,基于角加速度反馈的控制回路采用角加速度计代替陀螺仪,其结构更加简单、成本低廉,并且具有更良好的控制效果。根据过载控制原理及机体纵向运动方程,可设计得到高动态飞行器纵向通道控制回路,如图3所示[5]。

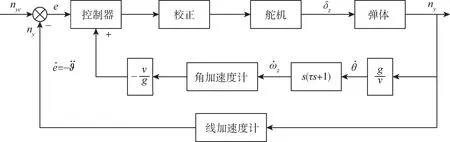
图3 角加速度控制回路Fig.3 Diagram of angular acceleration control loop

该控制系统的输入为横向过载指令nyc,且同样包含有内、外两个反馈回路: 角加速度计安装在机体的z轴上,用来测量角速度变化率;线加速度计安装在机体的y轴上,用来测量横向过载ny。

2 自动驾驶仪自抗扰过载控制系统设计

由于高动态飞行器作为被控对象存在的大范围不确定性,文本采用自抗扰控制方法对自动驾驶仪进行设计: 在上述传统控制方案的基础上,利用扩张状态观测器对系统内的不确定因素进行实时估计和补偿[14-15]。该自抗扰控制系统的设计重点在于对被控对象建立二阶数学模型以及控制器参数的调整。

为后续对两种不同控制方法进行稳定性对比,使自抗扰控制系统被控对象的动力学模型与1.3 节中PI 控制系统一致,其数学模型即为传递函数。自抗扰控制系统本质上可以理解为是一种添加了扩张状态观测器的PID 控制,其控制原理可简化为图4所示[16]。

图4 自抗扰控制系统简化原理示意图Fig.4 Simplified schematic diagram of active disturbance rejection control system

图4中,取纵向舵偏角δz作为（s）的输入信号u,ny为（s）的输出,将式（8）转化为微分方程形式可得

可将式（18）写为

式（19）中,f为被控对象的总扰动,其包含了内部扰动和外部扰动;b0为扩张状态观测器的增益。在实际工程中,控制器的设计一般都是基于一些已知的平衡点,且飞行器实际速度是可测的。b与飞行器速度有关,因此可根据平衡点处的速度信息进行计算。

假设系统的状态变量为:x1=ny、x2=、x3=f,x3为被扩张的状态变量。根据式（18）、式（19）得到系统被控对象（s）的状态空间模型

为使控制系统能对上述扰动项实时补偿,需要实现对不确定项的实时估计[17]。因此,在自抗扰控制系统中,构造三阶扩张状态观测器用于对外部扰动和系统未建模部分进行估计,其状态空间模型为

式（21）中,z1、z2、z3为x1、x2、x3的估计值,β01、β02、β03为扩张状态观测器的误差反馈增益[11]。

通过调节参数值,可以使z3准确估计模型不确定性及干扰。状态空间方程可整理为

采用带宽法整定自抗扰控制器及扩张状态观测器的参数: 通过配置控制器的带宽来配置控制器增益,并通过观测器的带宽来调节ESO 的各项增益。假设ωo为观测器的带宽,则其特征多项式为

进而,可得:β01=3ωo、β02=3ω2o、β03=ω3o。通过确定观测器带宽ωo即可确定各误差反馈增益,利用扩张状态观测器得到系统总扰动f的估计值z3=。利用的补偿作用消除被控对象的总扰动f,将原对象转化为纯二阶积分环节

由于角加速度制导回路相比角速度制导回路在控制效果等方面更具优势,自抗扰控制系统的控制器部分基于前者进行设计,如图5所示。该控制器利用角加速度计测量值及实际过载ny作为反馈,扩张状态观测器仅将总扰动估计值z3作为反馈,以提高系统的抗扰性能并稳定过渡过程。系统的控制律为

式（25）中,kp、kd为控制器的比例系数、微分系数。

假设控制器的带宽为ωc,结合图5的控制律得到其特征多项式为

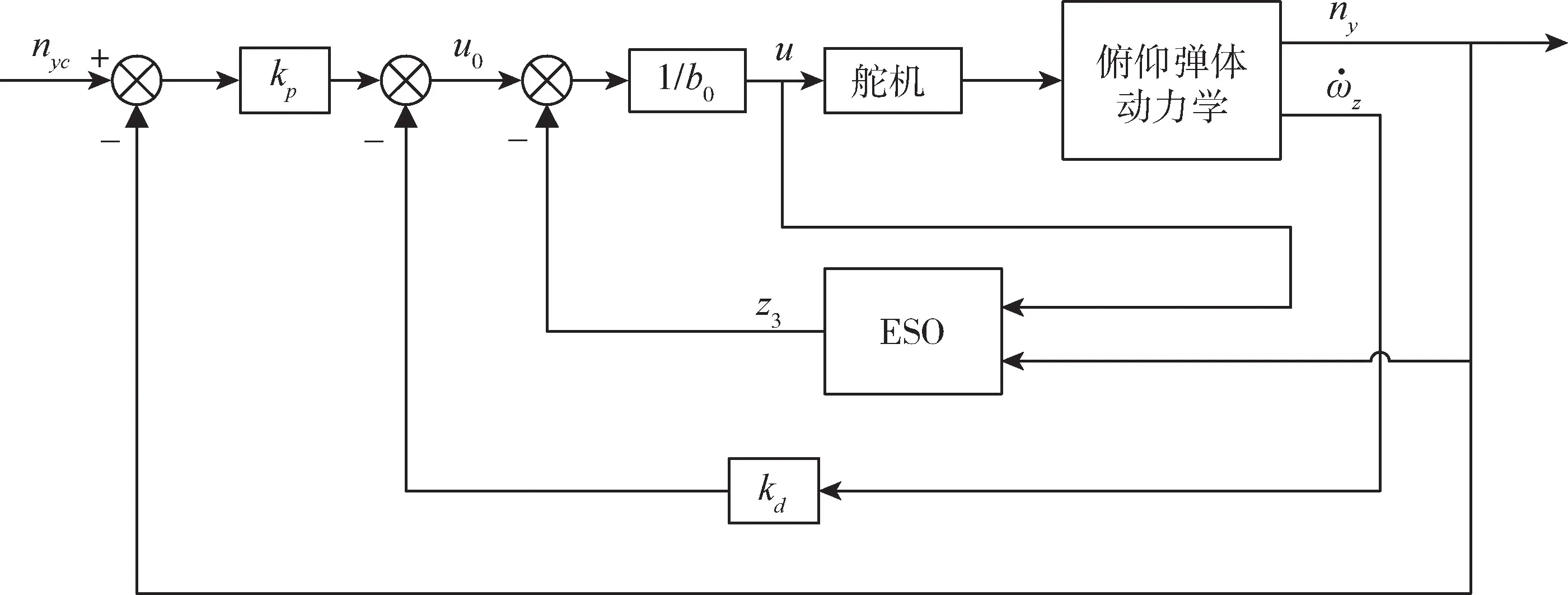
图5 角加速度反馈自抗扰过载控制原理图Fig.5 Schematic diagram of angular acceleration feedback active disturbance rejection overload control

可得:kp=ω2c、kd=2ωcv/g。因此,可通过调整控制器带宽ωc来确定控制器参数。

3 自抗扰过载控制系统稳定性分析

为对自抗扰控制系统进行频域分析,需求得自抗扰过载控制系统的等效闭环传递函数。根据文献[16]的二自由度控制结构方法,将自抗扰过载控制系统转化为二自由度PID 形式,如图6所示。在该控制框架下,环内控制器Gc（s）和前置滤波器F（s）可以进行独立设计,使系统具有两个自由度,因此被称为二自由度系统。其中,环内控制器Gc（s）用于抑制扰动,前置滤波器F（s）则能更好地满足系统对输入指令的跟踪特性。

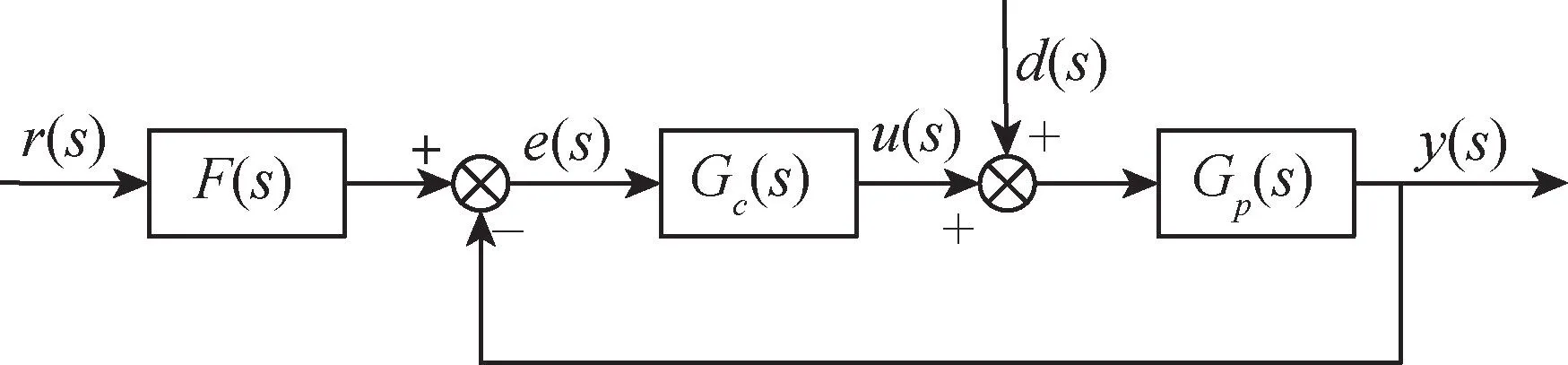
图6 经典二自由度控制结构Fig.6 Diagram of classical two-degree-of-freedom control structure

等效闭环传递函数Gcl（s）为

式（27） 中,被控对象Gp（s） 即为传递函数。

由扩张状态观测器的状态空间表达式（式（22））及控制律（式（24）、式（25））得到与nyc、y的关系如下

进而得到z与nyc、y的关系

将式（24）、式（25）代入式（29）中,得到

将式（31）代入式（27）中得到等效闭环传递函数,可由该传递函数对自抗扰控制系统进行频域分析

4 实验仿真与分析

高动态飞行器从发射到到达目标点的整个飞行过程中,其自身参数会因飞行高度、飞行速度等因素不断变化,因此机体作为被控对象是一个变参数环节。本文无法对飞行轨迹上每个点进行分析,所以选取飞行过程中代表飞行特性的6 个特征点,各参数如表1所示[18]。在特征点处对数学模型进行分析,用于对前文的控制回路进行比较。

表1 飞行轨迹上各特征点的参数Table 1 Parameters of each feature point on the flight path

4.1 角加速度与角速度反馈控制对比分析

为便于后续各控制回路的比较分析,将1.3 节中两种过载控制模型简化为经典PID 控制回路,并进行频域分析。

由于角加速度计和线加速度计的动态响应过程很快,固有频率较大,其频率响应位于高频段,因此可以忽略其影响。将角加速度计、线加速度计的相关信息在回路中进行简化处理,同时不考虑舵机动力学补偿,则可以将图3转化为图7的控制回路。其中,控制器采用两回路PI 经典自动驾驶控制,角加速度计的动力学模型简化为一微分环节,由式（16）得到其传递函数为

图7 简化角加速度反馈PI 控制回路Fig.7 Diagram of simplified angular acceleration feedback PI control loop

与角加速度反馈控制回路同理,经过简化处理可以将图2转化为图8的控制回路。高动态飞行器控制器同样采用传统PI 控制,该回路中角速度计的数学模型可根据式（16）简化为一比例环节

图8 简化角速度反馈PI 控制回路Fig.8 Diagram of simplified angular velocity feedback PI control loop

根据系统的性能指标要求选取一组理想闭环极点,由此计算出各个特征点处的自动驾驶仪控制参数,包括PI 控制器系数kp、ki和角加速度计（陀螺仪）的反馈系数kd,如表2所示。

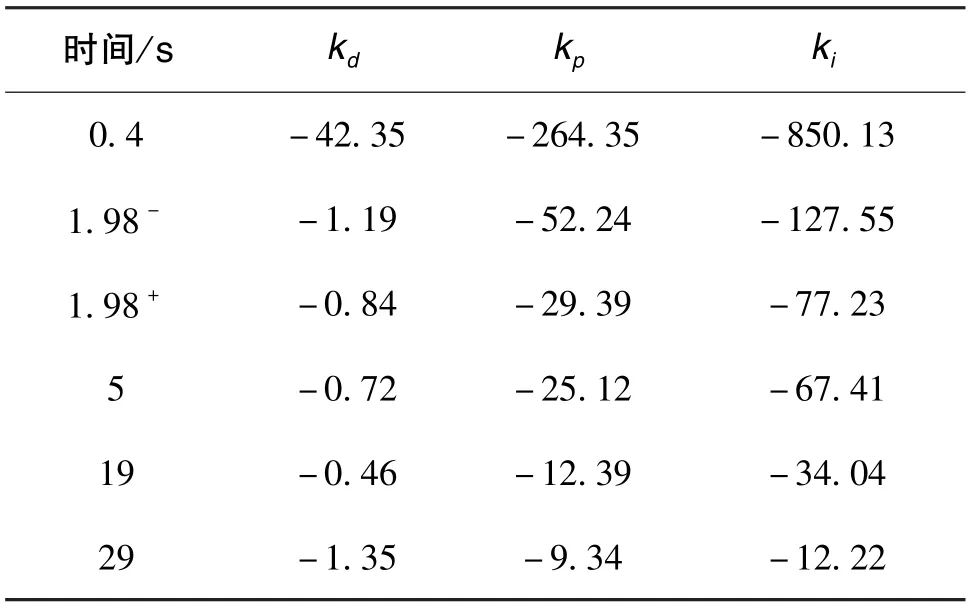
表2 各特征点处的参数设计值Table 2 Design values of parameters at each feature point

为便于直观比较两种控制回路的性能,选取其中一个特征点,在相同参数条件下进行仿真比对。取29s 时的飞行特征点,得到控制回路参数:v=300m/s、b=- 30.6483s-2、g1=43.5041s-2、g2=3.0210s-1。令输入过载指令为nyc=5g,得到的动态响应如图9所示。

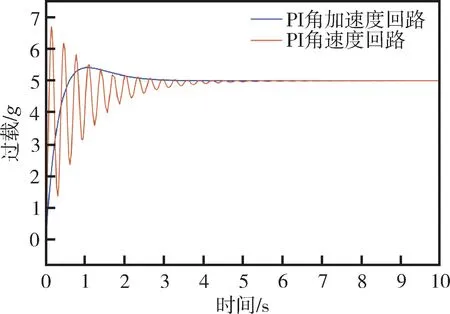
图9 角加速度回路及角速度回路动态响应Fig.9 Dynamic response of angular acceleration loop and angular velocity loop

采用经典控制理论对系统稳定性进行分析,在相同参数条件下对比角加速度回路与角速度回路的开环Bode 图,如图10所示。

由图9可知,在所选的特征点处,角加速度回路控制系统稳定,动态响应速度较快,但仍存在一定超调;而在相同条件下角速度回路系统不稳定,动态响应存在大幅震荡。由图10可知,角加速度回路的相角裕度为74°,而角速度幅值裕度为9°,综合分析可知,前者的稳定性能优于后者。进一步,仿真得到各个特征点上两种回路的相角裕度、幅值裕度和穿越频率等稳定性指标,如表3、表4所示。

图10 角加速度回路及角速度回路Bode 图对比Fig.10 Bode diagram comparison of angular acceleration loop and angular velocity loop

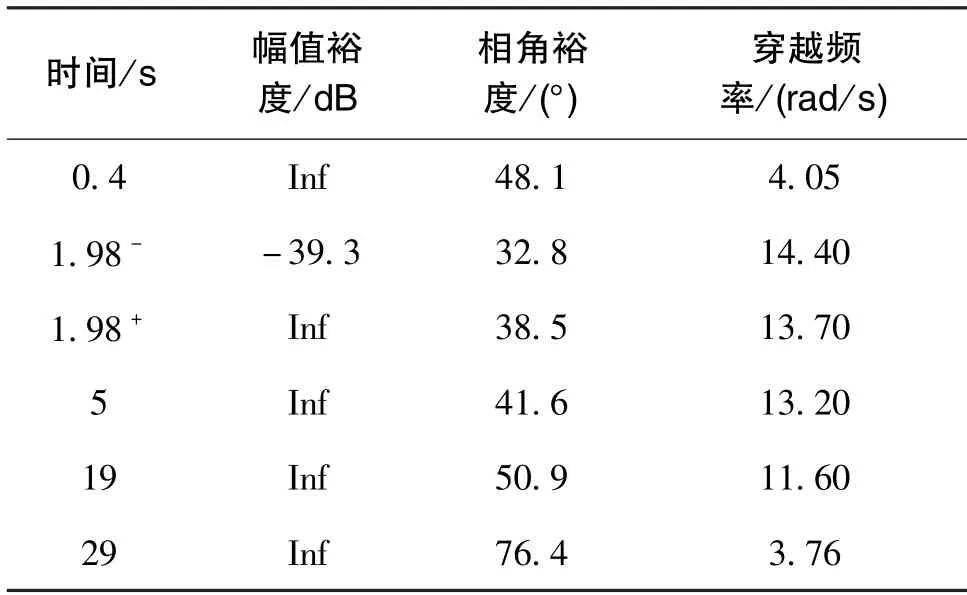
表3 各特征点上角加速度回路的稳定性指标Table 3 Stability indexes of angular acceleration loop at each feature point

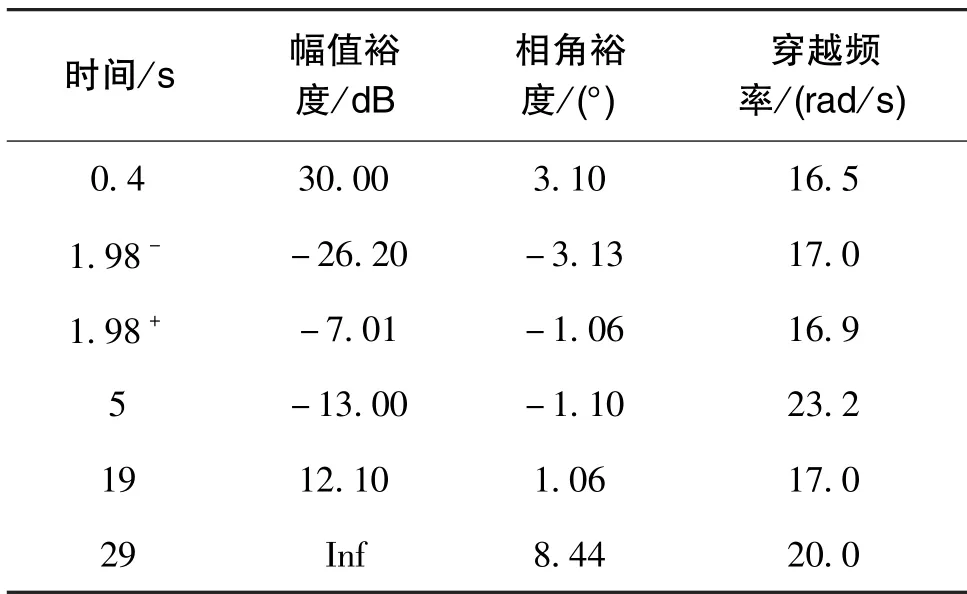
表4 各特征点上角速度回路的稳定性指标Table 4 Stability index of angular velocity loop at each feature point

由表3、表4可知,在飞行轨迹的各个特征点上,角加速度回路相比角速度回路均具有更高的幅值裕度、相角裕度和穿越频率,因此采用角加速度制导回路的高动态飞行器在整个飞行过程中具有更高的稳定性能。综合比较可知,在经典PI 控制系统中,角加速度反馈比角速度反馈能更有效地提高系统的动态响应性能和稳定性。

4.2 ADRC 与PI 控制对比分析

对自抗扰过载控制系统进行仿真分析,调节b0、ωo、ωc等参数,如表5所示,得到系统动态响应曲线如图11所示。由图11可知,PI 角加速度回路动态响应存在8.4%的超调量,在2.5s 时达到稳态;而ADRC 回路则不存在超调,且能在0.5s时达到稳态。对比可知,在相同条件下,自抗扰控制系统的动态响应超调量减小,跟踪效果明显优于传统PID 控制系统。

表5 自抗扰控制系统参数数据Table 5 Data of active disturbance rejection control system parameters

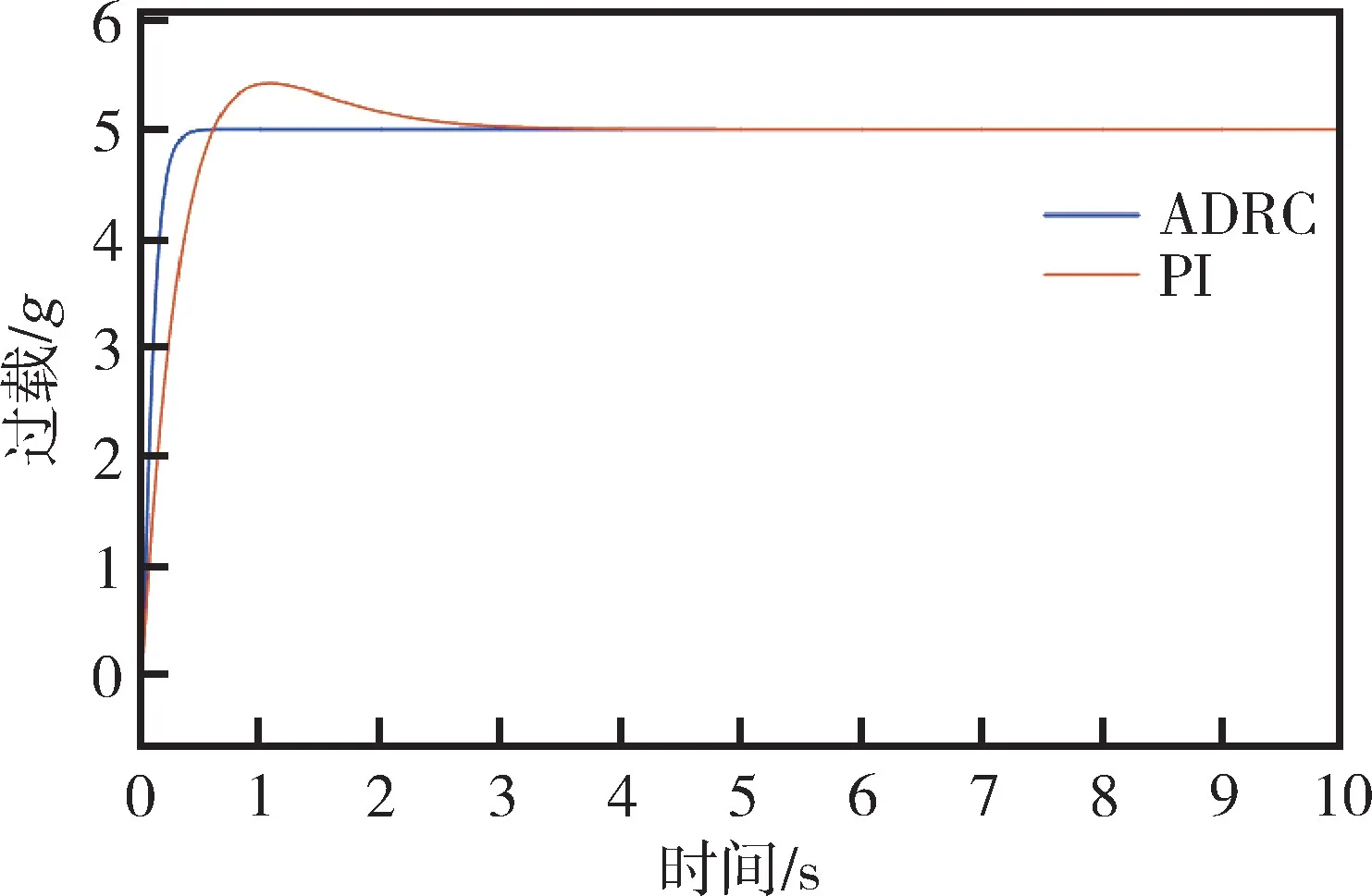
图11 ADRC 与PI 角加速度回路动态响应Fig.11 Dynamic response of ADRC and PI angular acceleration loop

由前文可知,自抗扰控制系统等效的二自由度系统由两部分串联组成,分别为前置滤波器F（s）以及由环内控制器Gc（s）和被控对象Gp（s）组成的闭环系统。由于前置滤波器F（s）用于改善输入指令的跟踪特性,而不影响后续被控过程,因此该系统的稳定性主要与后半部分即等效PID 控制的内环系统有关。取该系统的开环传递函数Gop（s）,通过PI与ADRC 角加速度回路的开环Bode 图分析系统的稳定性能,如图12所示。Gop（s）表达式为

由图12可知,ADRC 回路的幅值裕度和相角裕度在大部分频率范围内均高于PI 回路。综合分析可得,自抗扰姿态控制系统与传统的带PI 校正的控制系统相比,其跟踪性能、抗干扰性能都有了明显的提升。

4.3 静稳定度对各控制回路稳定裕度影响

以静稳定度为例研究机体参数变化对各控制回路稳定性能的影响,选取表1中29s 时的特征点参数,通过数值仿真分析各系统的稳定性能。同时取不同静稳定特性下的飞行器参数,即令恢复动力系数aα为41.54、0、-41.54,分别对应机体的静稳定、静中立、静不稳定状态,其他参数不变[19]。被控对象即传递函数（s）的开环Bode 图如图13所示。

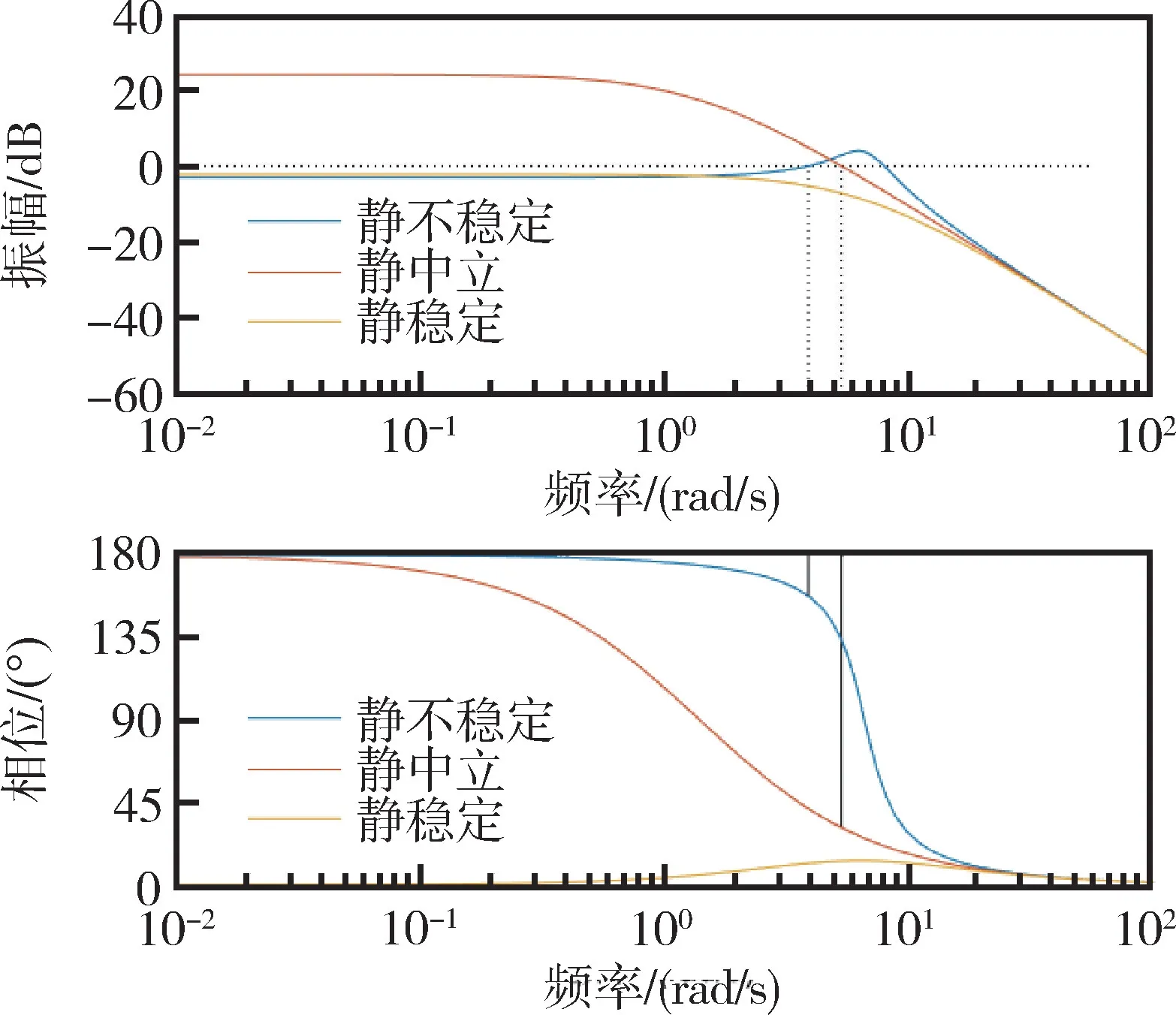
图13 不同静稳定度对应的机体动力学传递函数开环Bode 图Fig.13 Open-loop Bode diagram of airframe dynamics transfer function corresponding to different static stability

取相同参数对角加速度反馈的PI 两回路过载控制系统及自抗扰控制系统进行仿真,得到其开环Bode 图如图14、图15所示。

对比图14和图15可知,在穿越频率处PI 角加速度回路的相角裕度在静不稳定、静中立、静稳定三种飞行状态之间依次相差约5°,而自抗扰控制系统在穿越频率处的相角裕度几乎不受静稳定度的影响。因此,后者对于被控对象参数变化有更高的容错率,其鲁棒性要强于前者。

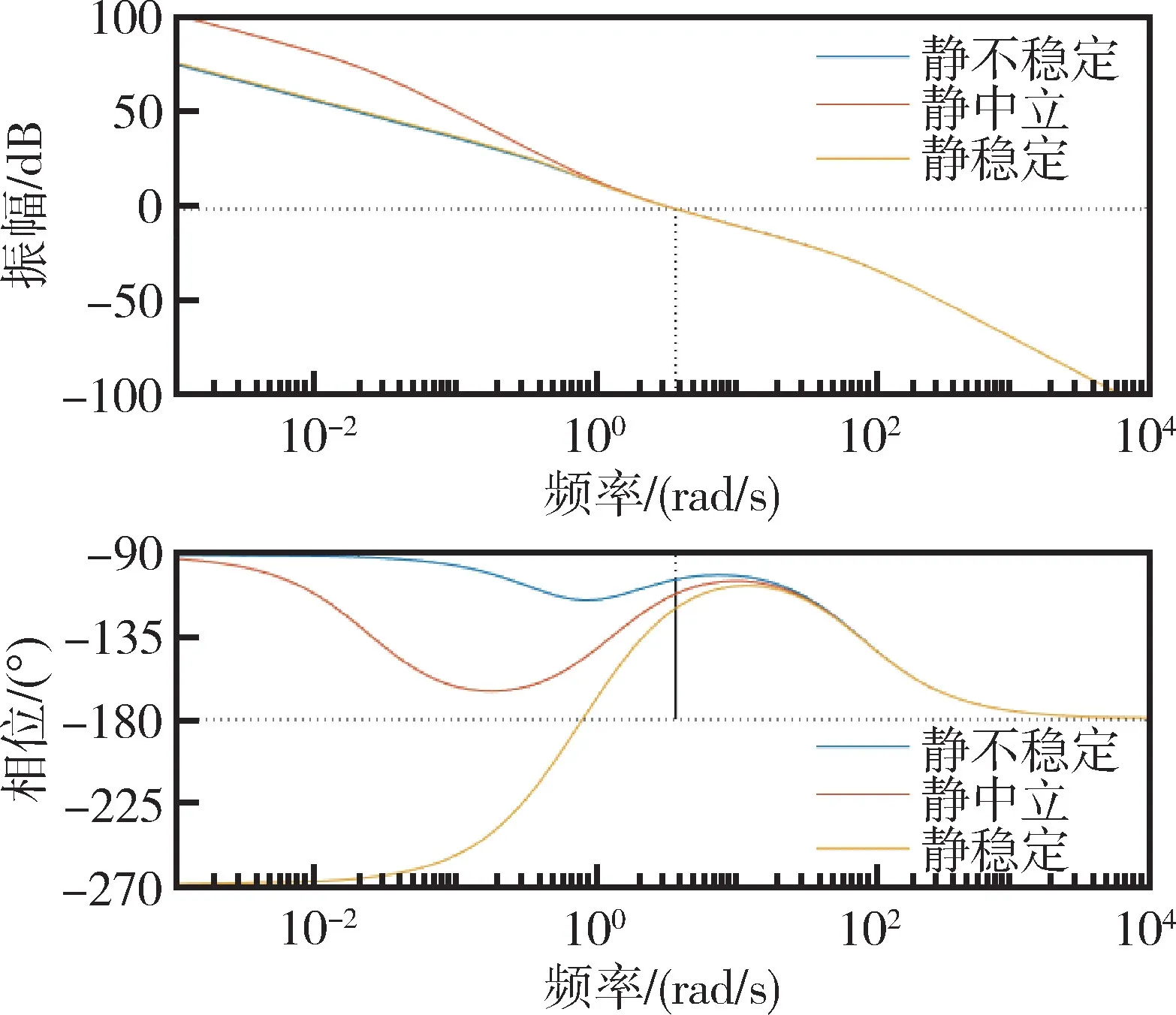
图14 不同静稳定度对应的PI 角加速度回路开环Bode 图Fig.14 Open-loop Bode diagram of PI angular acceleration loop corresponding to different static stability

图15 不同静稳定度对应的自抗扰过载控制开环Bode 图Fig.15 Open-loop Bode diagram of ADRC overload control corresponding to different static stability

5 结论

本文对比了以角速度和角加速度作为反馈的两种经典PI 两回路自动驾驶仪控制回路,并在角加速度反馈过载控制回路的基础上设计了自抗扰控制系统,对其进行了仿真校验及稳定性理论分析,得到结论如下:

1）传统的带PI 校正的过载控制回路中,角加速度反馈的控制方案相比角速度反馈,具有更好的跟踪性能和稳定性;

2）在高动态飞行器过载控制系统中加入自抗扰控制器,可对模型的不确定性及干扰进行补偿,明显提高了系统的稳定性能;

3）在控制系统参数变化时,自抗扰控制系统的稳定性几乎不受影响,表明其对模型的不确定性有较强的容错率,相比传统PI 控制回路拥有更好的鲁棒性。

在后续工作中,还需进一步优化自抗扰控制系统的结构,分析系统的抗干扰性能,并研究其余系统参数变化对稳定性能的影响,以完善系统鲁棒性的相关结论。此外,本文各控制回路的仿真结果均是在机体参数、控制参数一致的情况下得到的,因此可基于以上对比结果,针对控制系统的结构和稳定性关系进行理论研究,提出关于系统稳定性度量准则的假设。