基于双惯性器件的角速度差分相对姿态测量方法

张 天,靳舒馨,王 强,刘 刚,刘铁成

（1.中国兵器工业计算机应用技术研究所,北京 100089;2.北京卫星导航中心,北京 100094; 3.清华大学电子工程系,北京 100084）

0 引言

相对位姿测量技术利用传感器的特征信息解算出被测物相对于载体的位置与姿态,广泛应用于航天器空间对接、机器人控制、头盔瞄准器中[1]。在诸多相对位姿测量手段中,惯性测量无需外部信号、计算消耗低并且积分稳定,能够在恶劣环境中维持稳定输出,通常作为位姿测量滤波器的核心状态量[2-3]。由于捷联惯导的姿态解算会随陀螺漂移产生累积误差,在惯性系中通常由GNSS、重力与磁强计、视觉等提供姿态观测信息,实时修正积分结果[4]。

想要通过惯性技术获得载体坐标系下被测物的相对姿态,一种思路使用被测物和载体上各自IMU,解算出被测物相对惯性系和载体相对惯性系的实时姿态,将这两个姿态对齐到载体坐标系中获取到相对姿态[5]。但在该方法中,由于被测物处于载体内部,GNSS、磁强计等信息无法用于结果修正,相对视觉测姿又难以引入到两个独立的捷联惯导解算中,这限制了该方法的应用范围[6]。

相对姿态解算的另一种思路是引入当前时刻的相对旋转矩阵Rrel,将两个IMU 所测角速度值变换为当前时刻被测物与载体的相对角速度,再积分得到被测物与载体的相对姿态[5]。在该方法中,视觉等相对位姿信息可直接用于惯性位姿测量结果修正[7],但当外部修正失效时（视觉测姿失效时）,每次解算时使用的相对旋转矩阵Rrel都由上一时刻的姿态解算得到,Rrel中的误差会随积分过程迅速累积,导致测量误差迅速增大[8]。目前,大部分研究集中于使用视觉与惯性姿态测量融合方法[9-10],而缺少相关研究验证纯惯性相对姿态测量的有效性与精度。

鉴于上述原因,为给出合理的惯性相对位姿测量方法,本文首先结合数学关系推导了相对姿态测量的递推公式,证明了角速度差分相对姿态测量方法是传统独立积分方法的等价变换。此后,根据推导过程给出了具体的简化算法,并对算法适用范围进行了分析。最后,为验证角速度差分相对姿态测量方法的正确性,搭建了实验平台,对算法进行了工程适用性验证。

1 差分姿态算法推导

1.1 捷联惯导姿态解算

首先给出捷联惯导姿态解算公式便于后续推导[7,11]。使用四元数来表示旋转,对于表征惯性系i系至捷联坐标系b系的旋转四元数Q,有变换四元数与坐标系旋转角速度微分方程

式（1）中,的获取满足

式（2）中,ωbib为捷联陀螺的输出,Cbn由姿态更新的最新值确定,ωnen和ωnie分别为位置速率和地球自转角速率。

其中,⊗为四元数乘法,有

对于相同采样时间间隔的角增量,采用Picard求解法求解四元数微分方程,在时间段tk至tk+1满足定轴转动条件时,有

其中,

式（5）中,旋转角Δθb（tk）的物理意义为tk-1时刻b系到tk时刻b系的旋转角度,Δθx、Δθy、Δθz为陀螺在采样时间间隔内补偿后的角增量。

1.2 相对旋转性质推导

为获得两个已知相对旋转关系旋转的矩阵指数运算性质,这里进行假设,两个初始时刻对齐于惯性坐标系i的两个坐标系——坐标系a与坐标系b,在一段微小的时间τ内,相对坐标系i存在微小旋转,记为θa与θb,如图1所示。根据式（4）,可得到这两个微小旋转

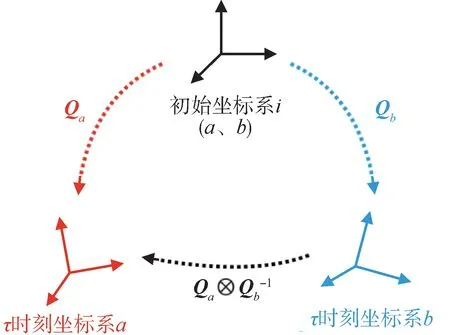
图1 相对惯性系的微小旋转示意图Fig.1 Schematic diagram of small rotation for relative inertial system

Qa与Qb为旋转发生后的两坐标系对应的旋转四元数。此时,坐标系b到坐标系a的相对旋转为

采用Picard 求解法求解四元数微分方程,在满足定轴转动条件时,微分方程的解为

该微分方程的解可以写为

式（10）中,的定义如下

根据定义可知: 式（11）中,物理含义为将b系相对i系的旋转运算M′（θb）通过M′（θa）的旋转操作,变换为a系中观察b系相对i系的旋转运算,即M′（θb）为从b系观察b系相对i系的旋转运算,而为从a系观察b系相对i系的旋转运算。

式（10）和式（11）表明了两个初始时刻对齐于惯性坐标系i的两个坐标系——坐标系a与坐标系b,在一段微小的时间τ内,相对坐标系i存在微小旋转,它们的相对旋转等同于将坐标系a与坐标系b的旋转都转换到坐标系a中,从a系观察两个坐标系相对运动的一次旋转。

简言之: 两个已知相对旋转关系的旋转矩阵,其指数函数的积等同于统一坐标系后差分旋转矩阵的指数函数。该相对旋转性质是差分测姿迭代算法推导的基础。

1.3 差分迭代算法推导

在被测物与载体的纯惯性差分测姿过程中,约定载体IMU 坐标系为p,被测物IMU 坐标系为h,空间坐标系为i。载体IMU 与载体固连,可在惯性系自由运动,被测物IMU 固连在被测物上与载体相对运动,具体如图2所示。

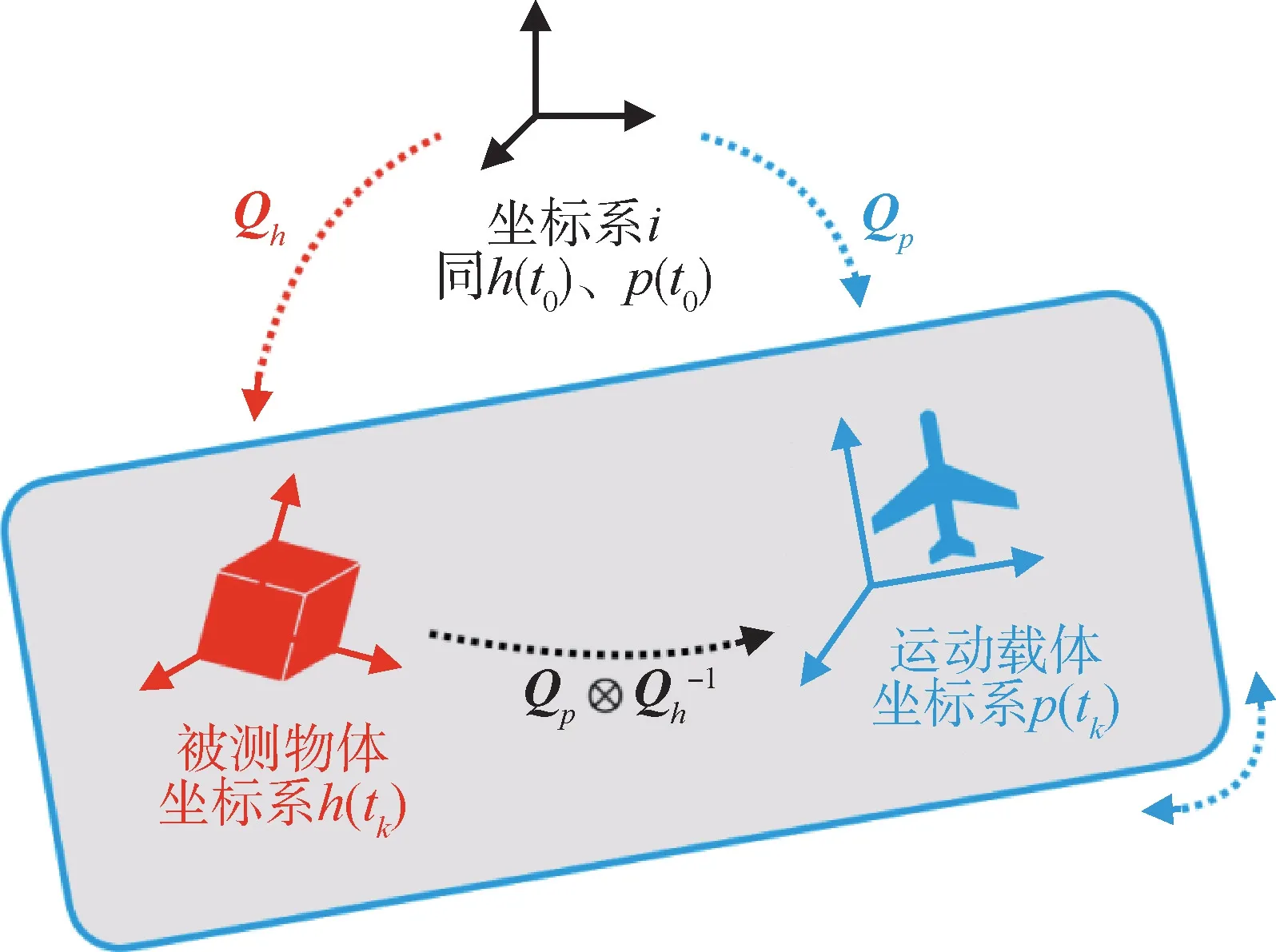
图2 运动载体中姿态测量的坐标系示意图Fig.2 Schematic diagram of coordinate system for attitude measurement in dynamic vehicles

根据上述坐标系定义分析相对运动条件下四元数微分方程的解。如果此时被测物坐标系到空间坐标系的旋转四元数Qh（tk）、载体坐标系到惯性坐标系的旋转四元数Qp（tk）已知,按照式（4）展开公式对Qh（tk）、Qp（tk）展开可得

定义k时刻被测物坐标系到载体坐标系的相对旋转为Qrel（tk）,则有

将式（12）、式（13）带入到式（14）中,有

式（16）表明了相对旋转四元数存在递推关系。依据1.2 小节推导的差分测姿运算性质公式（式（10））,使用表示载体坐标系下观察tk-1时刻至tk时刻被测物IMU 的旋转角度,带入式（16）中,将指数函数的积变换为统一坐标系后差分旋转矩阵的指数函数,有

根据相对旋转的积分关系,相对旋转可以写为角速度的积分形式

式（18） 中,Rrel（tk-1）为tk-1时刻的相对旋转矩阵,可以与相对旋转四元数Qrel（tk-1）相互转换,带入整理得到Qrel（tk）与角速度相关的递推公式

式（15）与式（19）表明,可以通过惯性系中载体角速度ωp（t）与惯性系中被测物角速度ωh（t）使用递推方法得到被测物相对载体的旋转四元数,其各自角速度解算后得到的姿态结果的差分等同于它们差分角速度的姿态解算结果。

2 两种算法比较

根据1.3 小节的讨论,分别利用两个惯性器件的角速度输出进行独立姿态解算,差分得到相对姿态结果的传统方法称为“独立积分法”;本文提出的使用两个角速度输出与当前时刻的相对旋转矩阵获取相对角速度,利用相对角速度积分得到相对姿态的方法称为“角速度差分法”。

在“独立积分法” 中,需要分别通过惯性积分计算被测物与惯性系、载体与惯性系的姿态信息,并在最后使用差分运算,获得被测物与载体的相对姿态。根据式（12）～式（15）,整理成算法如下:

1）根据被测物与载体的捷联惯导获取角速度信息ωh（t）与ωp（t）,计算当前时刻角增量Δθh（tk）与Δθp（tk）

2）使用当前时刻角增量Δθh（tk）与Δθp（tk）计算四元数独立积分Qh（tk）与Qp（tk）

3）使用独立积分Qh（tk）与Qp（tk）计算相对旋转四元数Qrel（tk）

在“角速度差分法” 中,在每一步使用上一次相对姿态的迭代结果,获取被测物与载体的相对角速度,再通过惯性积分直接获得被测物相对载体的姿态信息。根据式（17）～式（19）,写成算法如下:

1）根据被测物与载体的捷联惯导获取角速度信息ωh（t）与ωp（t）,计算当前时刻相对角增量Δθrel（tk）

2）使用当前时刻相对角增量Δθrel（tk）计算相对旋转四元数Qrel（tk）

对比“独立积分法” 与“角速度差分法”,从算法精度上看,二者均使用ωh（t）与ωp（t）作为捷联惯导解算输入量,均使用了Δt内的Picard 求解法求解四元数微分方程,具有相同的定轴转动边界条件,因此不考虑计算舍入误差的影响时,二者的理论精度基本相同。可以近似认为独立积分方法与直接差分方法具有基本相同的解算效果,这两种相对姿态测量的主要误差均源自捷联惯导中陀螺仪采样误差。

从算法的便捷性上看,直接差分方法相比独立积分方法获取Qrel（tk）的单次解算计算量更小,并且计算过程中引入了实时迭代的Rrel（tk-1）,便于滤波器外部观测接入时修正惯性测量引起的相对误差,是一种在工程上更具实用价值的惯性相对测姿算法。

3 实验设计

3.1 双IMU 数据同步采集

为验证差分测姿算法的有效性,选用两个IMU分别安装在载体上和被测物上,通过MCU 进行同步数据采集。考虑到载体的机动性,选用体积小、质量小、具有同步触发功能的IMU 进行数据采集实验[12-13]。在本实验中,选型ADI 公司的六轴微机电惯性测量单元ADIS16475,该传感器常温漂移量小于5（°） /h、量程大于300（°） /s,接近战术级精度,满足短时测姿精度需求[14]。该IMU 对外数据接口为SPI 总线,最高采样频率为2kHz,具备同步触发功能,可实现惯性数据的高频实时采集。

为实现两个IMU 同步触发,设计被测物上与载体上的两个IMU 的硬件电路原理如图3所示。两个MCU（微控制单元） 电路采用外部12V 供电,使用SPI 接口采集各自IMU 数据,采集频率为500Hz,并每隔1s 同步一次系统时钟。采集后的IMU 数据汇总到载体MCU 后传输到测试计算机中标记时间戳,用于后续数据处理。按照上述原理设计的被测物上MCU 电路与IMU 实物如图4所示。

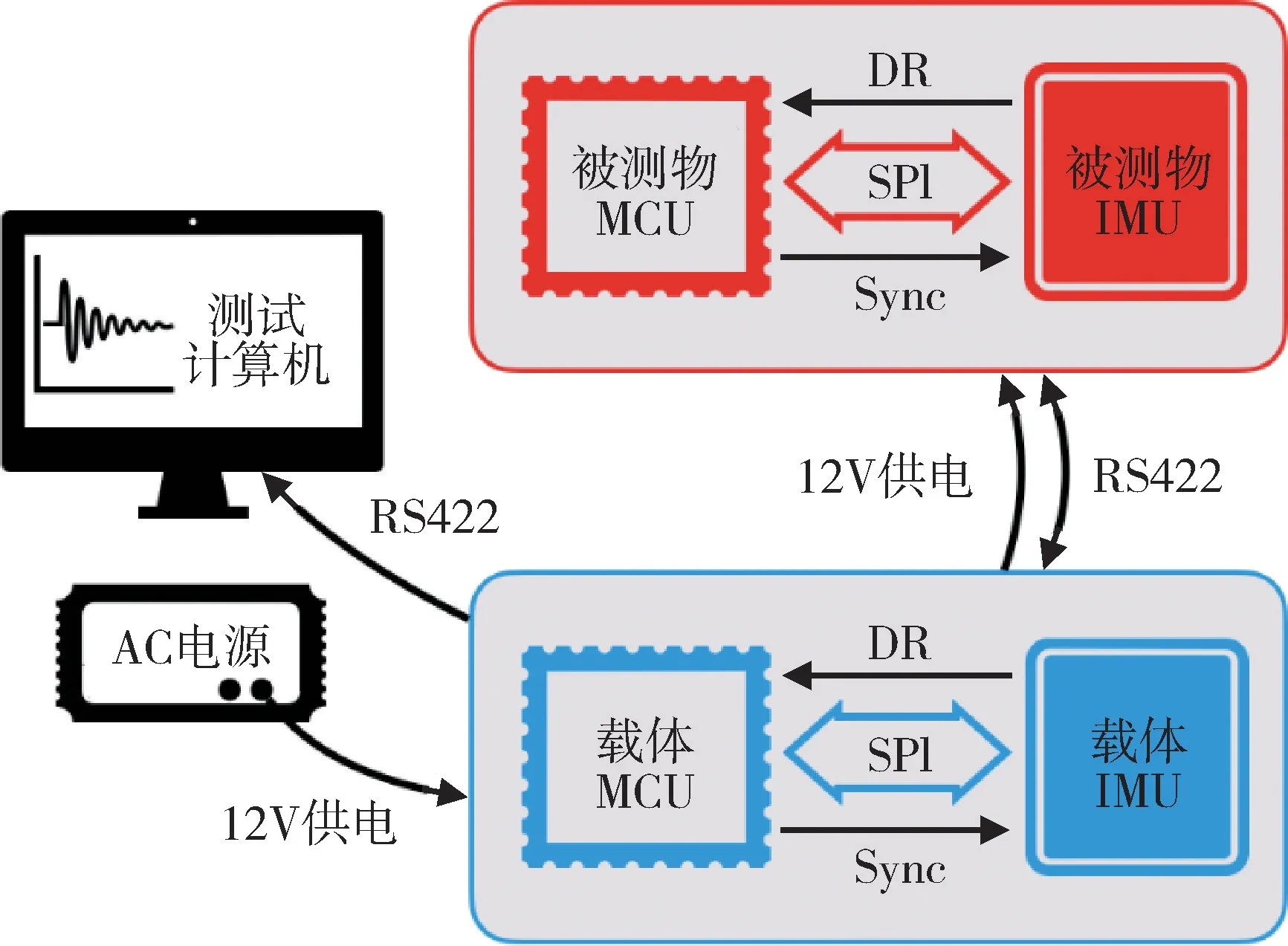
图3 搭载双IMU 的最小系统Fig.3 Diagram of minimum system equipped with dual IMU

图4 被测物上MCU 电路与IMU 实物Fig.4 Diagram of MCU circuit and IMU on the tested object

3.2 差分测姿环境搭建

为模拟载体运动,使用六个机械电缸驱动的六自由度并联运动台,通过控制器的运动学解算产生X轴、Y轴、Z轴的三轴平动以及围绕横滚轴、俯仰轴、航向轴的三个旋转运动[15]。本实验采用的六自由度运动台平动精度优于1mm,运动范围优于±0.3m,角运动精度优于0.1°,运动范围优于±20°,响应延迟优于10ms,可模拟载体常规运动。按照使用习惯定义该六自由度运动台模拟载体运动轴向,如图5所示。

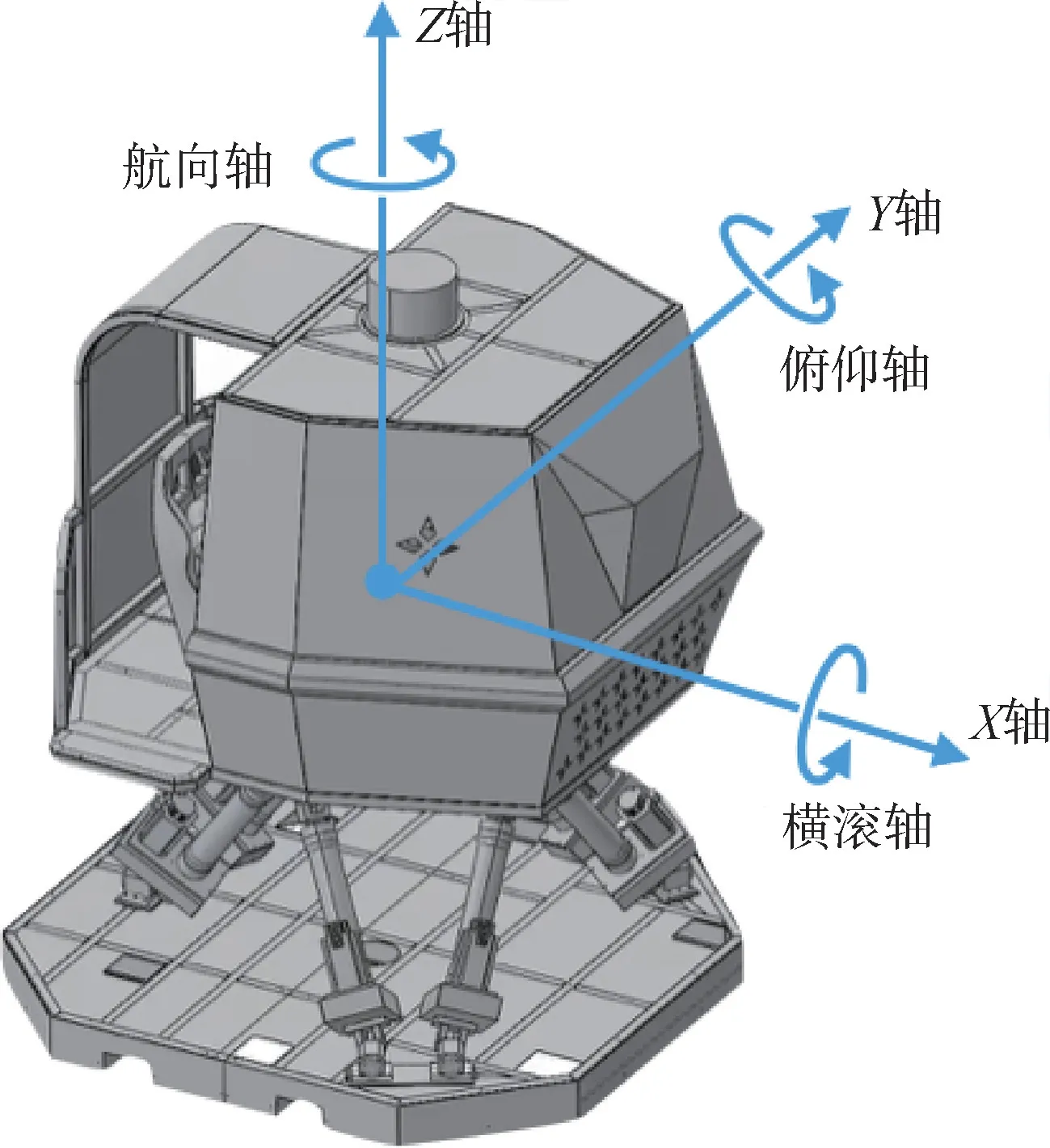
图5 载体运动轴向的定义Fig.5 Definition of the carrier motion axis

为模拟双IMU 差分工作环境,在六自由度运动台上的安装基准面上设置载体IMU 以及搭载被测物IMU 的双轴转台,原理如图6所示。其中,高精度双轴旋转台安装在六自由度运动台的安装基准面上,模拟被测物与载体的俯仰角与航向角相对姿态运动。该双轴转台可在航向角与俯仰角上连续运动,角度反馈精度优于0.01°。被测物IMU 设置在双轴旋转台的俯仰轴平台上,通过安装调整将IMU 敏感轴与转台运动轴对齐。载体IMU 设置在六自由度运动台的安装基准面上,通过安装调整将IMU 敏感轴与六自由度运动台的运动轴重合。

图6 相对姿态测量实验原理图Fig.6 Schematic diagram of relative attitude measurement experiment

按照上述原理搭建的测试环境如图7所示。完成实验环境布置后进行设备标定,将被测物IMU、载体IMU 坐标系对齐,开始数据采集。

图7 相对姿态测量实验环境Fig.7 Diagram of relative attitude measurement experimental environment

3.3 测姿数据采集

在双IMU 差分实验中,六自由度运动台的各轴以不同频率做正弦运动模拟载体自由运动。实验中的运动幅值、频率与相位选取考虑到载体的较大运动范围以及避免运动轴周期重合,设定X轴平动幅值50mm、频率0.25Hz、相位20°,Y轴平动幅值50mm、频率0.3Hz、相位50°,Z轴平动幅值50mm、频率0.2Hz、相位70°,俯仰轴幅值10°、频率0.1Hz、相位90°,横滚轴幅值10°、频率0.12Hz、相位0°,航向轴幅值180°、频率0.05Hz、相位40°。各运动轴幅值、频率、相位如表1所示。

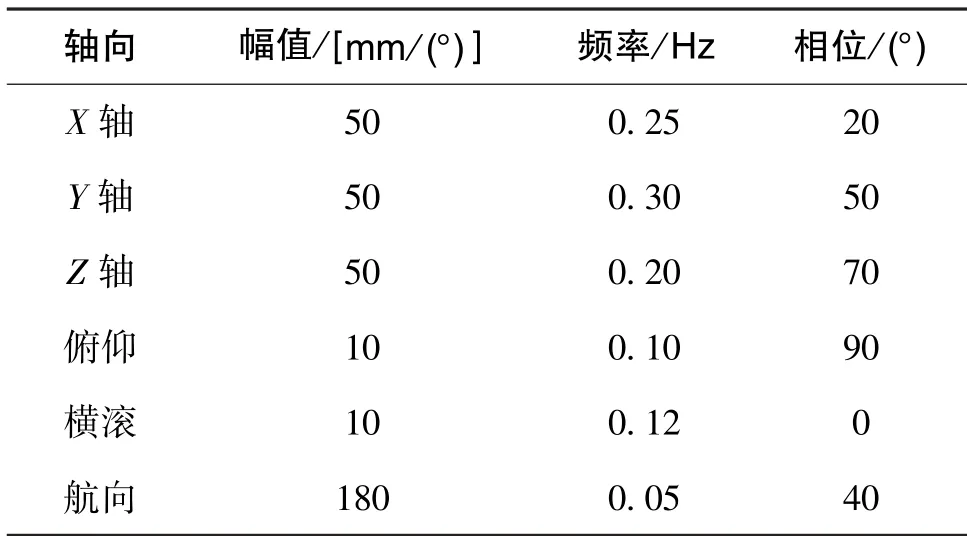
表1 载体六轴正弦运动Table 1 Six-axis sinusoidal movement of the carrier

双轴转台进行一组覆盖航向角与俯仰角运动范围的定点运动,其运动按照如下的方式生成:将双轴转台航向角范围（-180°～180°）和俯仰角范围（-75°～75°）均匀划分为20 个区域,并在每个航向角区域、俯仰角区域内随机选取一个角度,获取20 个航向角角度、20 个俯仰角角度,再从20个航向角与20 个俯仰角中不放回抽取,依次组合成为20 个姿态角。在本实验中,随机生成的20 组双轴转台运动的姿态角如表2所示。

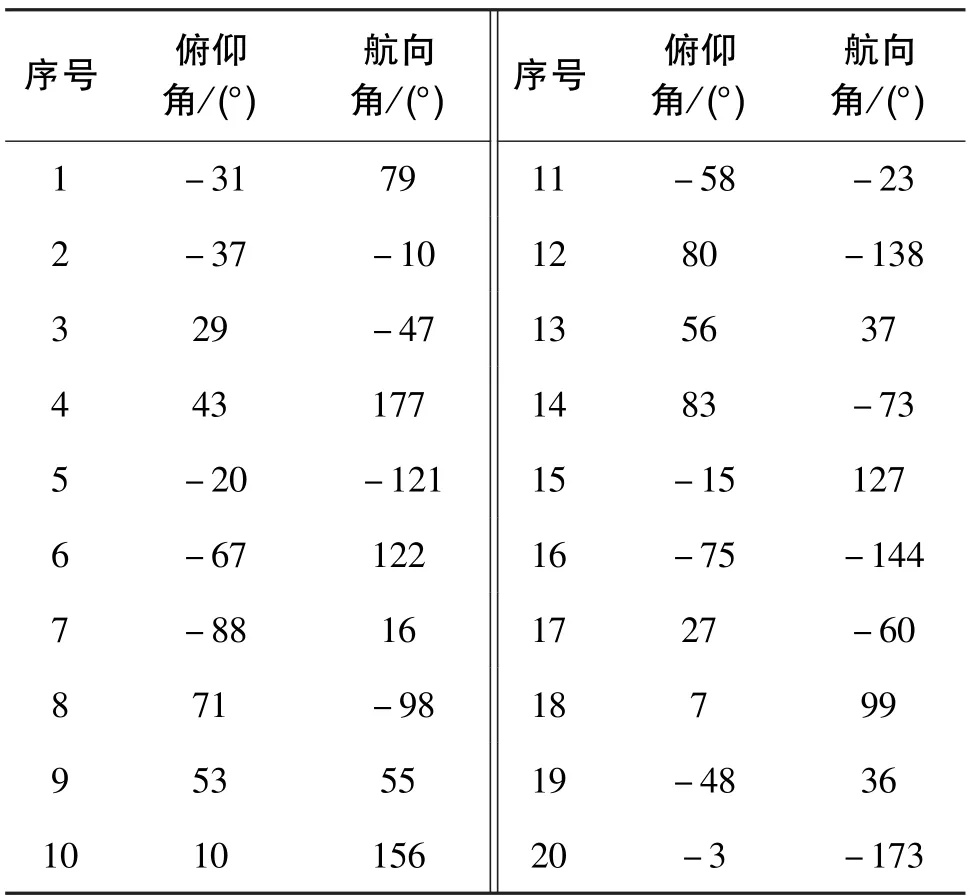
表2 双轴转台运动的姿态角Table 2 Attitude angles of two-axis turntable movement

完成上述运动数据准备后,按照如下顺序进行双IMU 差分测试数据采集实验:

1）开启六自由度运动台,使运动台六轴按表1做不同频的正弦运动以模拟载体自由运动情况;

2）开启测试计算机,开始双IMU 差分数据采集,在收到IMU 数据时标记时间戳并记录;

3）控制双轴转台按照表2从零位出发,依次运动到20 个姿态角,每个角度运行到位置后采集5s数据,20 个姿态角运行完成后,双轴转台回到零位;

4）结束数据记录并停止六自由度运动台,结束数据采集实验。

3.4 数据分析

使用“独立积分法” 与“角速度差分法” 对数据进行处理,选取俯仰轴数据与转台回传的真实数据进行比较,如图8所示。可以看出,在450s 内,两种测姿方法在20 个选取姿态角位置点的解算数据几乎与转台真实数据相同,三条曲线几乎重合。为了更清晰地观察测姿结果的准确性,选取7 号位置点局部放大,如图9所示。可以看出,独立积分法与角速度差分法的测姿输出曲线几乎重合,与转台真值相比存在一定测姿误差。

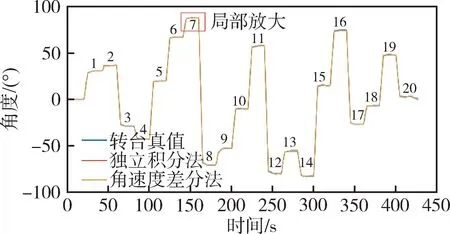
图8 俯仰角测姿数据与转台实际数据对比Fig.8 Comparison of pitch angle attitude measurement data with actual turntable data

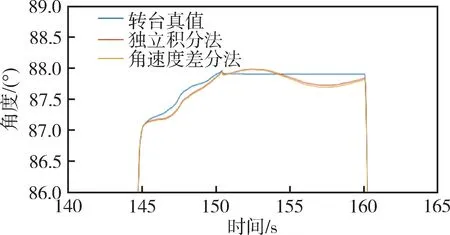
图9 俯仰角测姿数据与转台实际数据对比局部放大图Fig.9 Partial enlarged view of comparison between pitch angle attitude measurement data and actual turntable data

将“独立积分法” 与“角速度差分法” 得到的俯仰轴测姿结果减去转台俯仰轴返回真值得到测姿误差,绘制测姿误差角度随时间变化曲线,如图10所示。可以看出,在450s 内,独立积分法的RMSE 为0.490°,角速度差分法的RMSE 为0.510°,两种测姿方式均具有较高的测姿准确性。

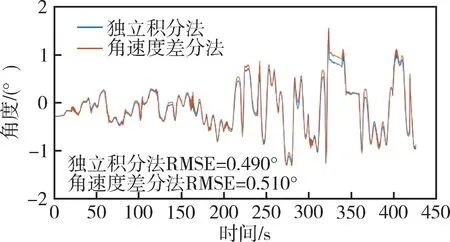
图10 俯仰角测姿误差Fig.10 Attitude measurement error of pitch angle

将两种测姿结果作差,绘制测姿差别随时间变化曲线,如图11所示。可以看出,两种测姿方式差别的RMSE 为0.060°,相较于约0.510°测姿误差RMSE,基本可以认为两种测姿方法等同。

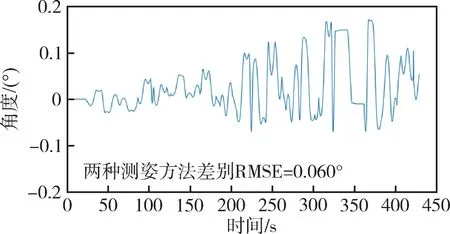
图11 俯仰角“独立积分” 与“角速度差分” 的差别Fig.11 Differences between independent integral and angular velocity difference for pitch angle

同样选取“独立积分法” 与“角速度差分法”的航向轴数据与转台回传的真实数据进行比较,如图12所示。可以看出,在450s 内,三条曲线几乎重合。为了更清晰地观察测姿结果的准确性,选取10 号位置点局部放大,如图13所示。可以看出,两种测姿方法的输出曲线几乎重合,与转台真值相比存在一定测姿误差。

图12 航向角测姿数据与转台实际数据对比Fig.12 Comparison of heading angle attitude measurement data with actual turntable data

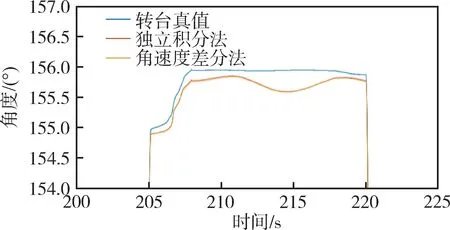
图13 航向角测姿数据与转台实际数据对比局部放大图Fig.13 Partial enlarged view of comparison between heading angle attitude measurement data and actual turntable data

将“独立积分法” 与“角速度差分法” 得到的航向轴测姿结果减去转台航向轴返回真值得到测姿误差,绘制测姿误差角度随时间变化曲线,如图14所示。可以看出,测姿误差在±1.5°范围内,独立积分法的RMSE 为0.372°,角速度差分法的RMSE 为0.372°,两种测姿方式均具有较高的测姿准确性。

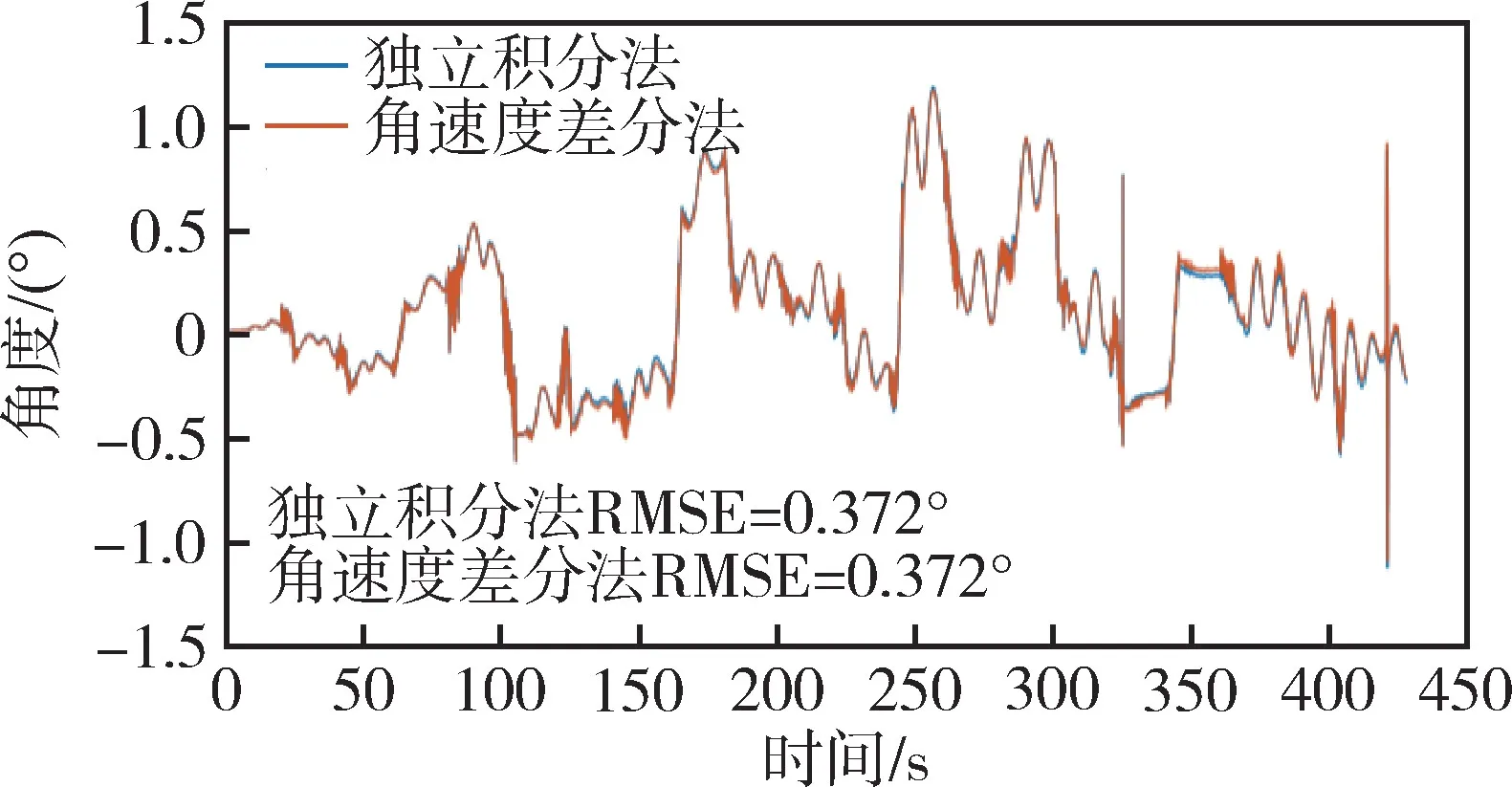
图14 航向角测姿误差Fig.14 Attitude measurement error of heading angle

将两种测姿结果作差,绘制测姿差别随时间变化曲线,如图15所示。可以看出,两种测姿方式差别的RMSE 为0.015°,相较于0.372°测姿RMSE,基本可以认为两种测姿方法等同。

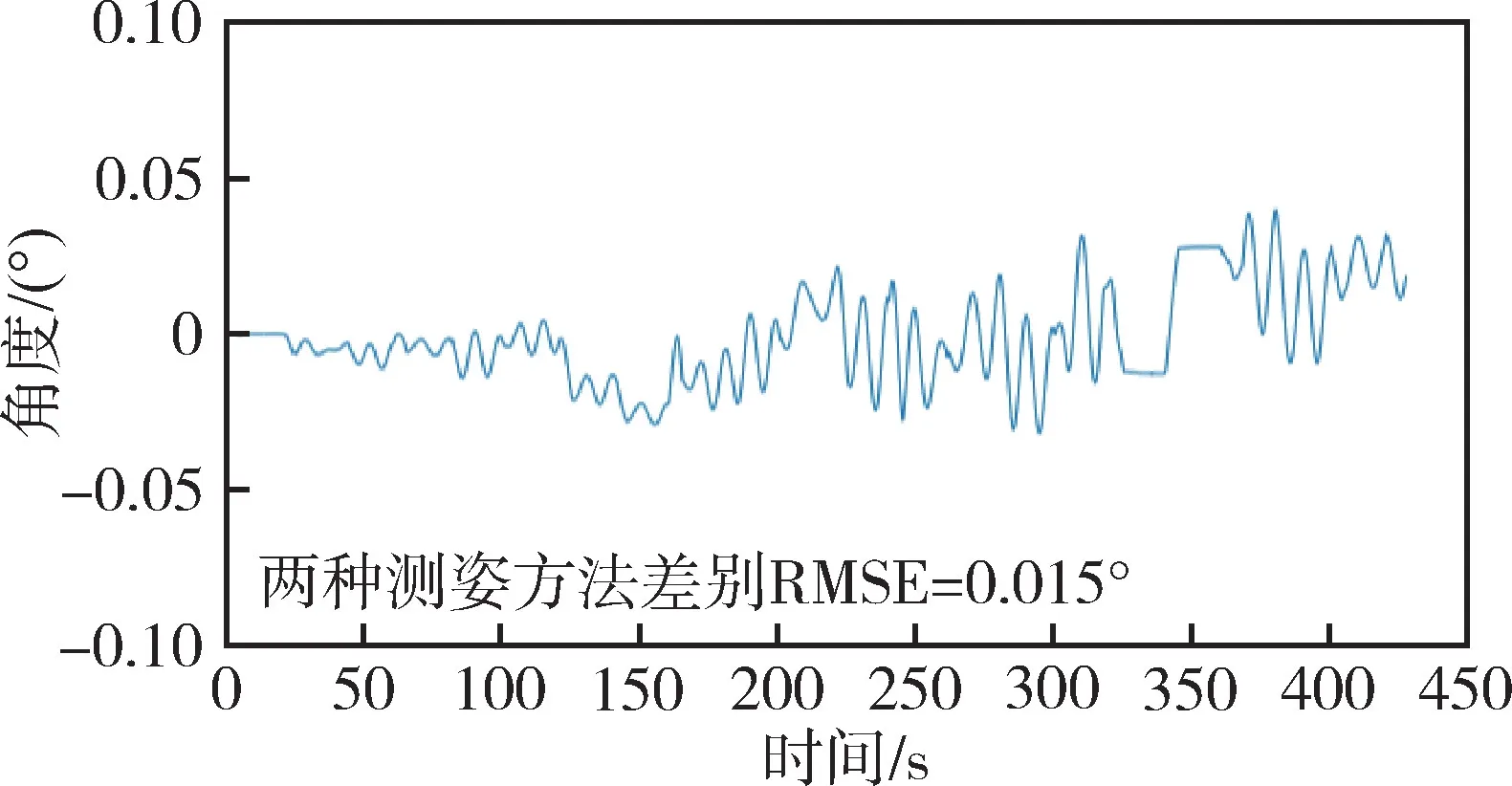
图15 航向角“独立积分” 与“角速度差分” 的差别Fig.15 Differences between independent integral and angular velocity difference for heading angle

将俯仰轴数据与航向轴数据对比可以看出,航向轴测姿精度略优于俯仰轴,该现象主要由双轴转台未修正的安装误差、六自由度运动台的高频振动对陀螺角速度输出的影响造成。

4 结论

本文从捷联惯导姿态解算出发,通过双IMU差分测姿公式推导,提出了一种基于双惯性器件的角速度差分相对姿态测量方法,并设计了双IMU差分测姿实验,从数学上与实际应用上证明了本文提出的“角速度差分法” 与传统“独立积分法”具有相同的测姿结果。从实验结果可以看出,“角速度差分法” 与“独立积分法” 两种差分测姿解算的偏差为0.060°（1σ,俯仰轴）与0.015°（1σ,航向轴）,均比0.510°（1σ,俯仰轴） 与0.372°（1σ,航向轴）的惯性测姿误差小1 个数量级,基本可以认为两种测姿方法等同。相较于传统的“独立积分法”,本文提出的“角速度差分法” 更便于引入外部观测量,构造滤波器,具有更强的工程适用性。后续可以围绕滤波器构造进一步探究,消除纯惯性差分测姿过程中的误差累积,进一步提升算法实用性。