基于高阶多项式的爬游机器人足端轨迹规划
戴 祯,刘卫东,徐景明,李 乐
(西北工业大学 航海学院,西安 710072)
0 引言
海洋是一个充满未知、领域广阔、可达性差的区域,近年来,人类对海洋的探索越来越深入。为了更好的认识海洋,开发海洋资源,世界各国都在大力发展水下机器人技术。对比几类典型机器人:轮式机器人在面对崎岖地形时移动速率大大降低;履带式机器人机动性差,在严重崎岖地形下,容易发生侧翻;而足式机器人在爬行运动时与地面接触点是一系列离散点,能够适应大多数非平坦结构地形,具有较强的灵活性,且不易侧翻[1-4]。因此,对具有海底爬行和水中巡游功能的水下爬游机器人的研究具有重要的意义。
水下爬游机器人能够在海底进行灵活爬行运动,需要对机器人足端位置进行轨迹规划。轨迹规划是采用时间序列信息对机器人足端的位置、速度等参数进行规划进而控制机器人足端空间位置与姿态[5-8]。常用的轨迹规划方法有贝塞尔曲线[9-10]、基于遗传算法的轨迹曲线[11]和B样条曲线[12]等。通过对机器人足端轨迹进行规划,使机械腿运动平滑,减少冲击和振动,对提高机械腿的稳定性、可靠性和工作效率有重要意义。文献[13] 为了解决机器人在运动过程中机械腿与机体之间存在的互斥力问题,提出了一种当机器人足端处于支撑相时,足端与跟关节的纵向距离保持恒定的直线行走方式,使机器人足端轨迹为平行于机体的直线轨迹,如图1所示。而对于机器人足端处于摆动相时,如何在空间中运动,并没有进行深入的研究。
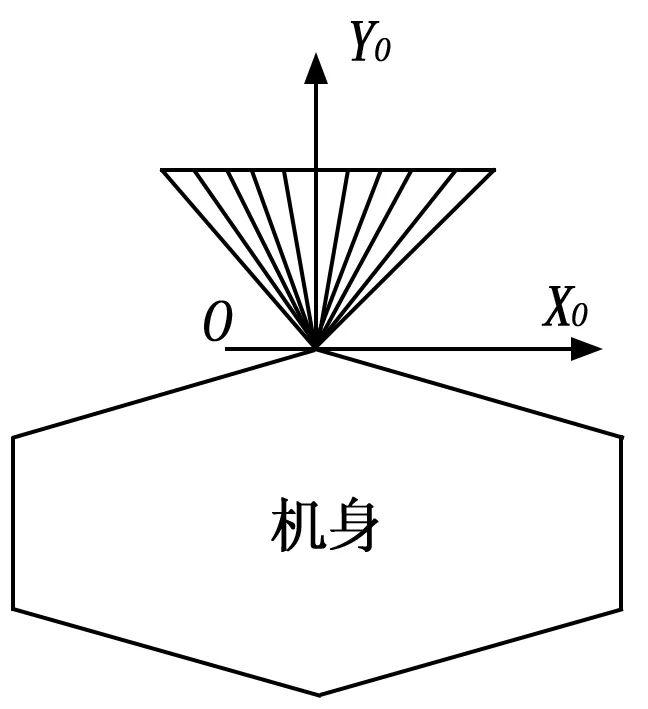
图1 机器人直线行走方式
文献[14] 采用一种改进B样条曲线的方法进行机器人足端轨迹规划,该方法能够有效提高机器人足端空间轨迹的平滑性,但所拟合的曲线不会经过其控制点,因此控制精度不高。
本文以水下爬游机器人为研究对象,为了使机器人具有良好的水下爬行运动能力,采用了一种直线和曲线相结合的机器人足端空间运动轨迹;利用四阶多项式和六阶多项式分别对水下爬游机器人足端轨迹进行规划,由于六阶多项式所规划的轨迹曲线包含其加速度约束比四阶多项式所规划的轨迹曲线包含的约束条件多,所以六阶多项式更适合用于本文所提出的足端空间运动轨迹规划。通过对机器人足端速度以及加速度的约束,使机器人足端轨迹在直线和曲线连接处的速度连续,解决了机械腿在运动过程中的抖动问题,使机械腿能够柔顺运动。
1 水下爬游机器人整体结构及建模
水下爬游机器人兼顾水中巡游和海底爬行运动能力,爬游机器人能够在复杂的海底环境中运动,其运动控制系统起到了至关重要的作用。运动控制系统在接收到爬行运动指令后,按照规划的运动步态解算出机器人各腿关节电机的角度,将解算结果通过多轴管理器发送至各关节电机,使机器人实现爬行运动。图2为水下爬游机器人整体结构示意图。

图2 水下爬游机器人整体结构
运动学建模是进行机器人轨迹规划及运动控制的基础。根据水下爬游机器人的结构,建立机器人的机体模型如图3所示。图中①、②、③、④分别表示爬游机器人的四条腿:①-左前腿、②-左后腿、③-右后腿、④-右前腿。机体坐标系的原点是爬游机器人的机体重心,Xb正向指向机器人前进方向,Yb正向指向右移方向,Zb正向垂直XbOYb平面竖直向上。d1表示前腿/后腿沿OYb轴偏移量,d2表示前腿/后腿沿OXb轴偏移量。
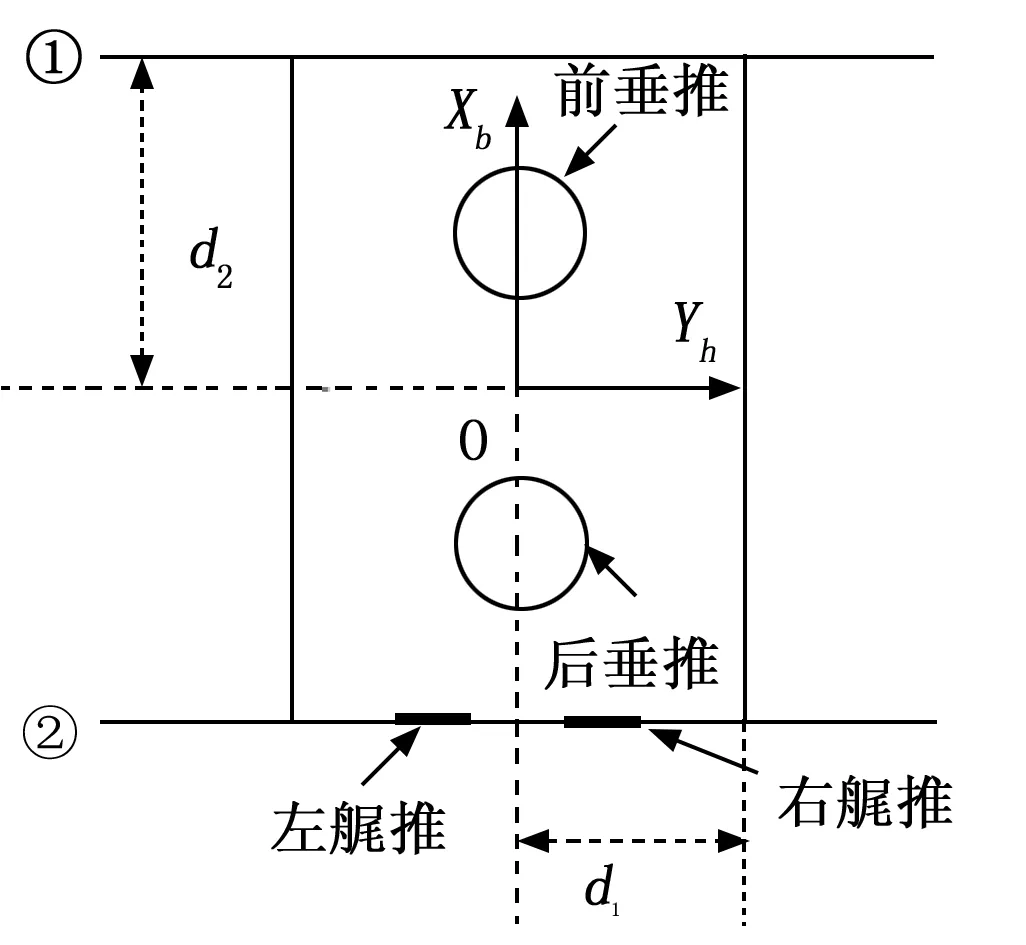
图3 水下爬游机器人机体模型
根据水下爬游机器人模型,对其进行运动学分析,利用数学方法推导出爬游机器人的正、逆运动学解[15-16],为水下爬游机器人运动控制奠定基础。
本文主要研究水下爬游机器人足端轨迹规划,首先需要求解机器人逆运动学。所谓逆运动学,即已知机器人足端在机体坐标系XbOYb下的位置坐标,反解出各腿关节角的过程[17]。已知腿部足端在机体坐标系下的坐标为(x,y,z),在求解跟关节处转角θ1的大小时,首先做出其单腿结构图,如图4(a)所示,(x,y)表示足端在机体坐标系XbOYb下的坐标,D为腿在支撑走一步过程中形成的足端轨迹与跟关节保持的恒定间隔距离,由正切函数定义:
(1)
在求解肩关节处转角θ2和膝关节处转角θ3时,对机械腿进行后视投影,得到在YbOZb平面的结构图,如图4(b)所示,(y,z)为腿在该平面下的足端坐标,b为足端在支撑走一步过程中,该腿跟关节与足端的连线距离,它与图4(a)中D的关系是:
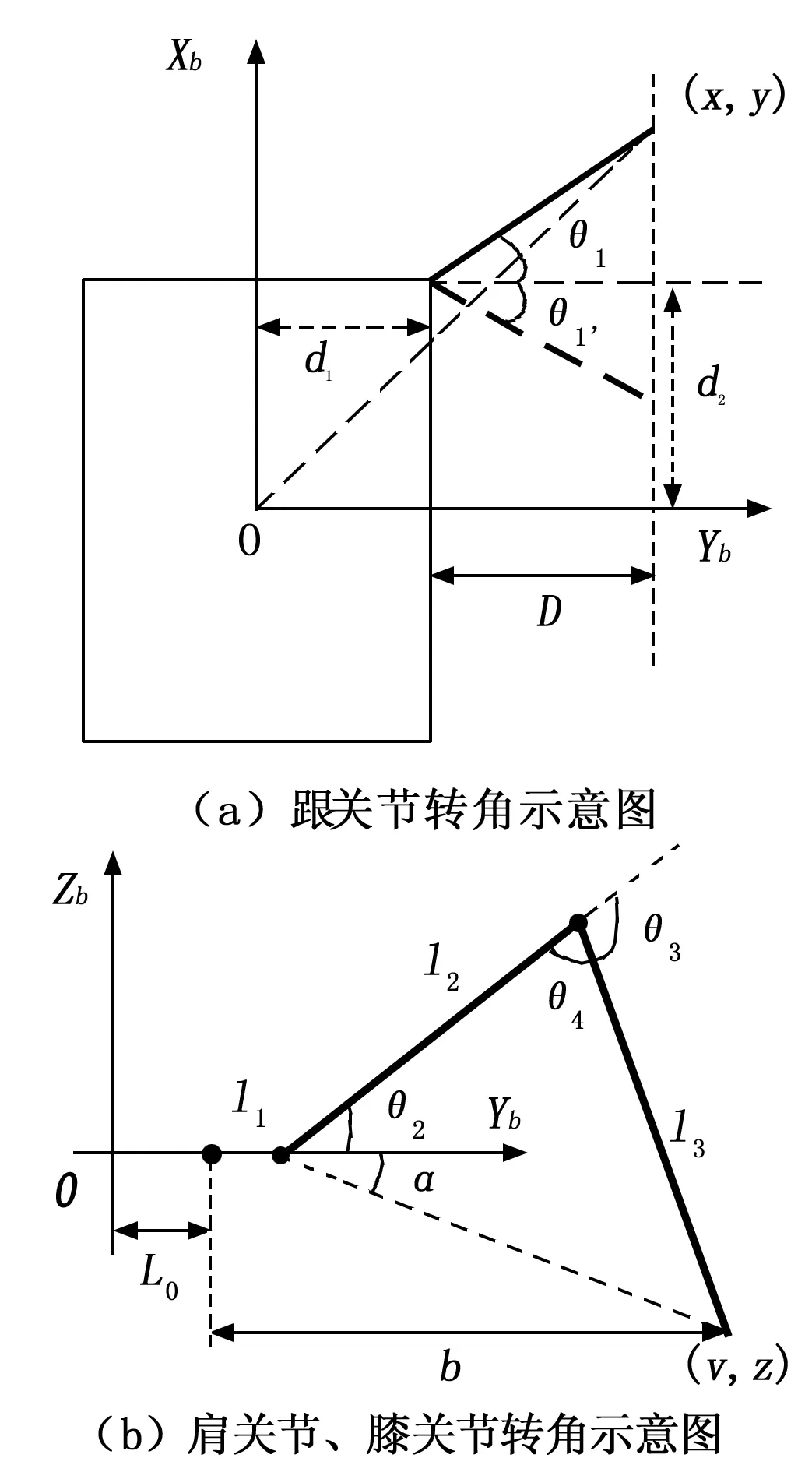
图4 机器人腿部结构
bcosθ1=D
(2)
解得θ2的值为:
(3)
同样的方法求解θ4,
(4)
(5)
则:
θ3=π-θ4
(6)
2 水下爬游机器人足端轨迹规划算法
水下爬游机器人足端轨迹规划所要解决的是机器人在爬行时的单腿足端轨迹生成问题,规划的意义在于既满足机器人运动的需要,又能根据机器人的结构、运动及动力特性对其运动进行约束,从而保证了机器人有序、稳定的运动。
通常机器人在运动的过程中与地面接触时会产生一定冲击,为了保证机械腿摆动过程中具有良好的启动和制动特性,减小足端与地面的冲击力,所以运动轨迹曲线除了规划足端参考点的起始点和终止点的位置外,还需要规划以上两点的速度和加速度特性。以往机器人爬行过程中的足端轨迹一般采用典型的直线型轨迹或者抛物线型轨迹[18-20],如图5所示。但是直线型轨迹在机械腿的柔顺控制方面表现较差,所以一般用抛物线型轨迹代替直线型轨迹,抛物线型轨迹不但解决了机械腿的柔顺控制问题而且具有更好的跃障能力,但是抛物线型轨迹在与地面接触或离开地面时足端会与地面产生一个切向力,会对机械腿关节和足端造成严重的机械磨损。
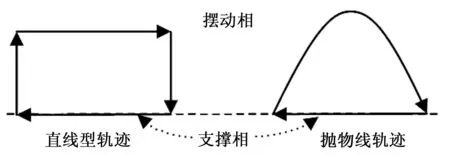
图5 典型机械腿末端轨迹曲线
本文提出一种曲线和直线相结合的足端轨迹。 如图6所示为机械腿运动一个周期内,足端在空间的运动轨迹示意图,当机器人处于静止状态时,足端端点为规划轨迹的中点,x为前进方向,z为竖直抬起方向,y方向为恒定值。为了更好的研究足端轨迹在空间中的特性,把图6中的轨迹划分为4个阶段,分别为摆动相的抬起阶段(AB)、摆动阶段(BCD)、下落阶段(DE)和支撑相的支撑平移阶段(EA),当机器人进行爬行运动时,机械腿末端始终处于空间中规划轨迹上的一点,并且满足一定的速度、加速度约束条件。
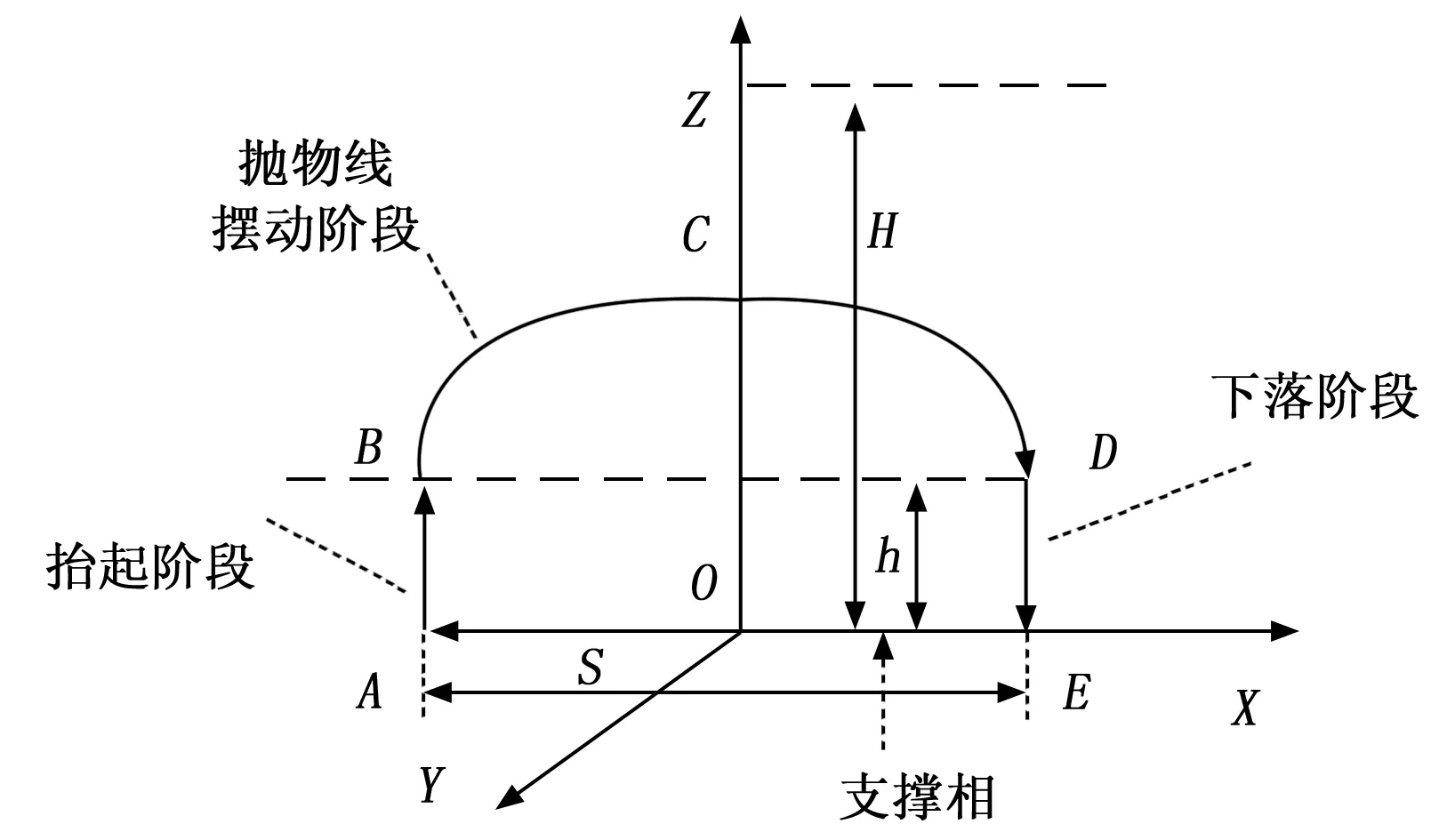
图6 爬游机器人足端空间轨迹
对于直线型轨迹,可以用简单的三次多项式策略进行规划,其形式为:
s(t)=c0+c1t+c2t2+c3t3
(7)
在时间T内足端从起点运动到终点,在起始处施加约束条件s(0)=s′(0)=0,在终点处施加s(T)=s′(T)=0的约束。在t=0和t=T时,对上式求导得:
s′(t)=c1+2c2t+3c3t2
(8)
通过以上4个约束条件求得多项式系数:c0=0,c1=0,c2=3/T2,c3=-2/T,但是本文所设计的足端轨迹存在曲线线段,需要确定一个中间点,如图6中的C点,所以采用四阶多项式来描述轨迹曲线:
s(t)=c0+c1t+c2t2+c3t3+c4t4
(9)
四阶多项式可以由起始点位置和速度,终止点位置和速度以及中间点位置唯一确定。但爬游机器人腿部控制还需要考虑轨迹起止点和终止点的加速度约束,所以选用六阶多项式来求解轨迹曲线,其数学表达为:
(10)
末端速度为:
(11)
末端加速度为:
(12)
当机器人足端处于摆动相时,假设所需要的时间是tw,起始抬起时刻为t0=0,向前摆动和竖直下落时刻为t1=tw/4、t2=3tw/4,足端抛物线摆动所用时间为t=tw/2。
以竖直抬起阶段AB段为例,六次多项式轨迹曲线求解方程:
(13)
然后利用轨迹曲线约束条件,即起止时刻的位置s(t0)、s(t1),速度v(t0)、v(t1),加速度a(t0)、a(t1)以及中间时刻的位置s(t1/2)就可以唯一确定一组解c0、c1、c2、c3、c4、c5、c6。
3 水下爬游机器人足端轨迹仿真与分析
针对本文提出的机器人足端轨迹,采用高阶多项式对其进行仿真分析,然后对多段轨迹连接点处的速度问题以及机器人足端抬起和下落过程中机械腿的抖动问题进行分析,通过设置相关运动参数,优化机器人足端轨迹速度以及加速度特性,使机器人在爬行过程中具有良好的运动控制性能。
3.1 机器人足端轨迹规划仿真分析
本文所采用的水下爬游机器人足端轨迹中每一段都相对独立,当约束条件中每一段的起始点速度和加速度,终止点速度和加速度都为0时,根据机械腿结构和其相关运动参数,求得爬游机器人爬行一步的轨迹曲线方程,如式(14)、(15)和(16):
y=-128
(14)
(15)
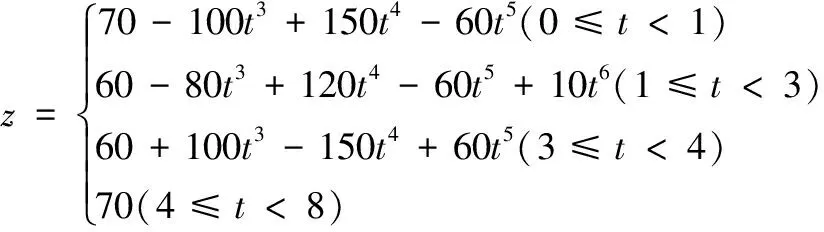
(16)
利用上述轨迹曲线方程,画出爬游机器人足端轨迹曲线如图7(a)所示,图7(b)为利用四阶多项式求解得到的机器人足端空间轨迹曲线。对比图7(a)、图7(b)中所示曲线并不能明显看出六阶多项式规划得到曲线的优势,分别对图7(a)、图7(b)中机器人足端轨迹曲线求二阶导,得到爬游机器人足端在空间中的加速度曲线,如图8(a)、8(b)所示。由于y分量在整个运动过程中保持恒定不变,所以只对轨迹z分量和x分量的加速度进行讨论。
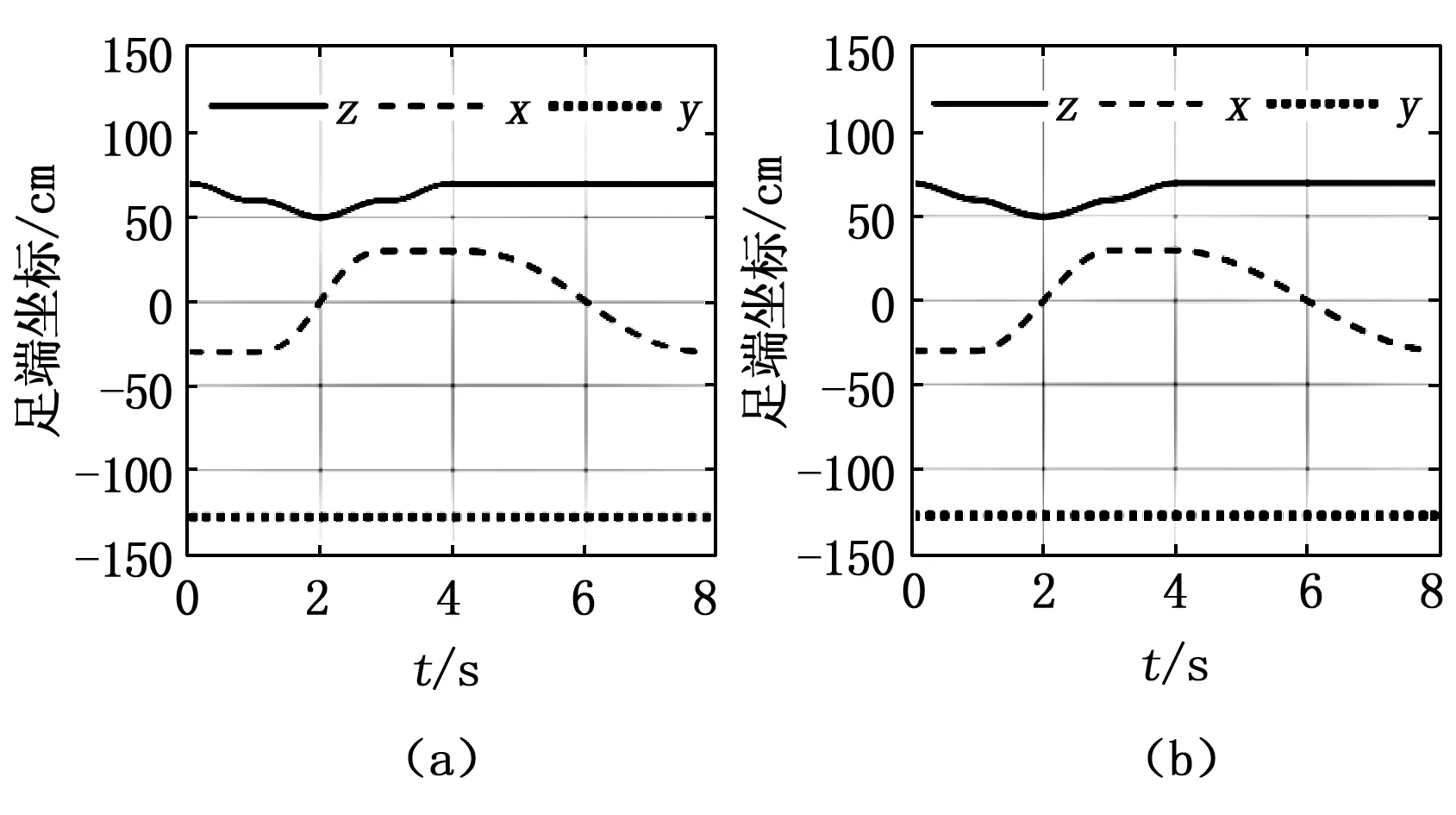
图7 爬游机器人足端轨迹曲线
对比分析图8(a)、图8(b),在整个运动过程中,利用六阶多项式规划得到的曲线加速度比四阶多项式规划得到的曲线加速度更光滑,而且加速度不会发生突变,这为机器人的柔顺控制奠定了基础。另外,在整个运动结束时刻,由于六阶多项式对机器人足端轨迹加速度存在约束作用,所以曲线加速度为0,而四阶多项式求解得到的加速度是一个不等于0的值,这样的加速度值会影响到下一阶段的运动控制,会使机械腿产生抖动,进而影响机器人整体运动控制效果。
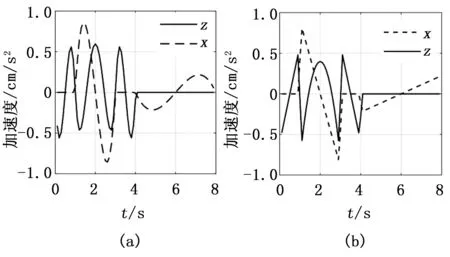
图8 爬游机器人足端加速度曲线
综上所述,六阶多项式不但可以约束机器人足端轨迹位置,还可以约束轨迹的速度以及加速度,因此,更适合本文所提出的水下爬游机器人足端轨迹规划。
六阶多项式所规划得到的轨迹曲线能够满足本文所研究的机器人足端轨迹曲线的性能要求。但结合图7(a)和图8(a)分析可知,首先在图7(a)中机器人足端轨迹曲线在z方向存在抖动;其次由于每执行完一段独立的轨迹,机器人足端速度就会为0。当机器人足端从A点运动到B点时速度就会为0,从B点经过C点运动到D点,整个过程中起始点和终止点机械腿末端的速度都为0,所以在图8(a)中,加速度曲线连续上下波动。如果机械腿末端在AB段运动结束之后保持匀速进入BCD段,在B点附近加速度则保持为0不变化。根据牛顿第二定律F=ma,当加速度为0时,机械腿关节电机力矩也等于0,这将意味着在整个运动过程中机械腿所消耗得能量将会减小。同时会消除两段轨迹连接处加速度连续波动问题,为机械腿的柔顺控制提供良好的基础。
3.2 机器人足端轨迹优化仿真分析
考虑到机器人在海底爬行运动时,会遇到各种复杂地形,为了使机器人适应不同地形,机械腿在抬起阶段速度快,而下落阶段速度缓慢,防止机器人足端与地面发生刚性接触。
根据以上分析,对机器人足端轨迹进行优化,重新设定机器人足端轨迹直线与曲线连接点处的约束条件为:v=vt(vt≠0)、a=0,同时使机器人足端抬起阶段,即AB段时间缩短,而下落阶段,即DE段时间增加,得到如图9所示为优化后的爬游机器人足端轨迹曲线与未优化的轨迹曲线图。
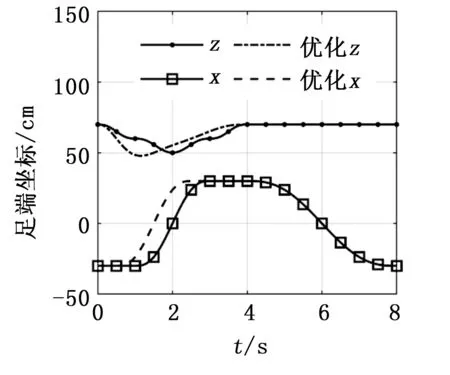
图9 优化前后机器人足端轨迹曲线
如图9所示,前4 s内机器人足端处于摆动相,优化后的轨迹曲线中消除了z分量的波动,而且比未优化的轨迹曲线提前到达了指定位置,后4 s机器人处于支撑相,优化后和优化前的曲线没有明显差别。而优化后的x分量相对于未优化之前响应时间缩短。对图9中轨迹曲线x分量和z分量求导得到轨迹的速度曲线如图10所示,对比分析图10中优化前和优化后的速度曲线可知,优化后z分量速度在机器人足端初始抬起阶段比未优化的速度值更大,而且在机器人足端摆动和下落阶段其波动性明显要小于优化前的值,这会使得机械腿足端的速度控制更加柔顺。另外,图10中x分量在足端抬起阶段相对于未优化的轨迹曲线其响应时间更短,而在下落阶段其所用时间延长,从而为足端接触地面过程中的运动控制提供条件。

图10 优化前后机器人足端速度
对图9中的机器人足端轨迹曲线求二阶导,得到相应加速度曲线如图11所示,图11中优化后的z分量加速度在机器人足端抬起阶段其值明显大于未优化的加速度值,而且在摆动阶段和下落阶段加速度波动的幅值明显小于优化前。相比较优化前x分量的加速度曲线,优化后的曲线响应速度更快,这一现象符合前面所提到的机器人足端快抬慢落的运动规律。
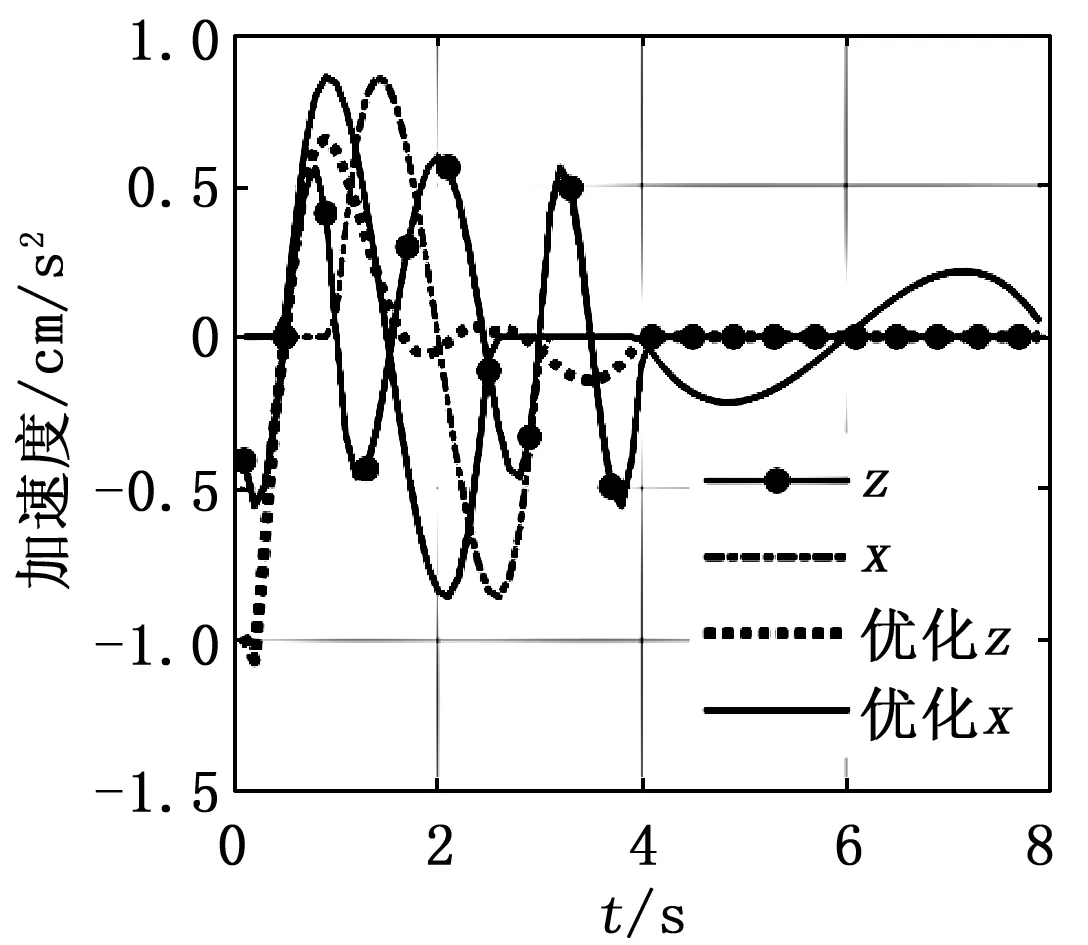
图11 优化前后机器人足端加速度
由以上分析可以得出结论,利用优化后的六次多项式轨迹规划方法所求解得到的足端轨迹曲线具有良好的运动性能,为机器人运动控制奠定了基础。
根据D-H法则,结合爬游机器人机械腿结构参数建立仿真模型,通过仿真得到机器人单腿足端在空间中的运动轨迹,如图12所示。图12中机器人足端首先竖直抬起,之后呈抛物线向前摆动,接着竖直下落进入支撑相,最后机器人足端向后平移,使机器人机体向前运动,这符合本文所规划的足端轨迹曲线。图12中ABCDEA为完整一步的空间轨迹,而OB′C′DEO为机器人足端从初始位置抬起行走半步的空间轨迹。机器人从支撑状态开始运动和运动结束时回到支撑状态都需要运动半步,保证机器人在运动开始时和运动结束时处于支撑状态。
4 爬游机器人水池爬行运动实验
基于以上所述机器人足端轨迹规划方法,经过仿真验证后,进一步在深度为20 m的水池环境中利用机器人实物样机进行试验。试验中机器人进行前进爬行运动,运动过程如图13所示,通过水面观察和水下相机记录,表明水下爬游机器人具有良好的爬行运动能力,且在运动过程中机械腿不再出现抖动,验证了本文所提出的基于高阶多项式的机器人足端轨迹规划算法的可行性和有效性。

图13 爬游机器人前进爬行运动
机器人在水底进行前进爬行运动时,其腿部各关节角度变化如图14所示。定义机体中心为机器人参考原点,各机械腿顺时针方向转动为机械腿跟关节的正方向,图14中,从起始点开始左前腿和右前腿跟关节角度都减小,而左后腿和右后腿跟关节角度都增大,说明机器人右前腿和左后腿处于摆动前进状态,左前腿和右后腿处于支撑向后状态。肩关节和膝关节随时间发生周期性变化以保证机器人足端在空间中始终处在同一平面内运动。
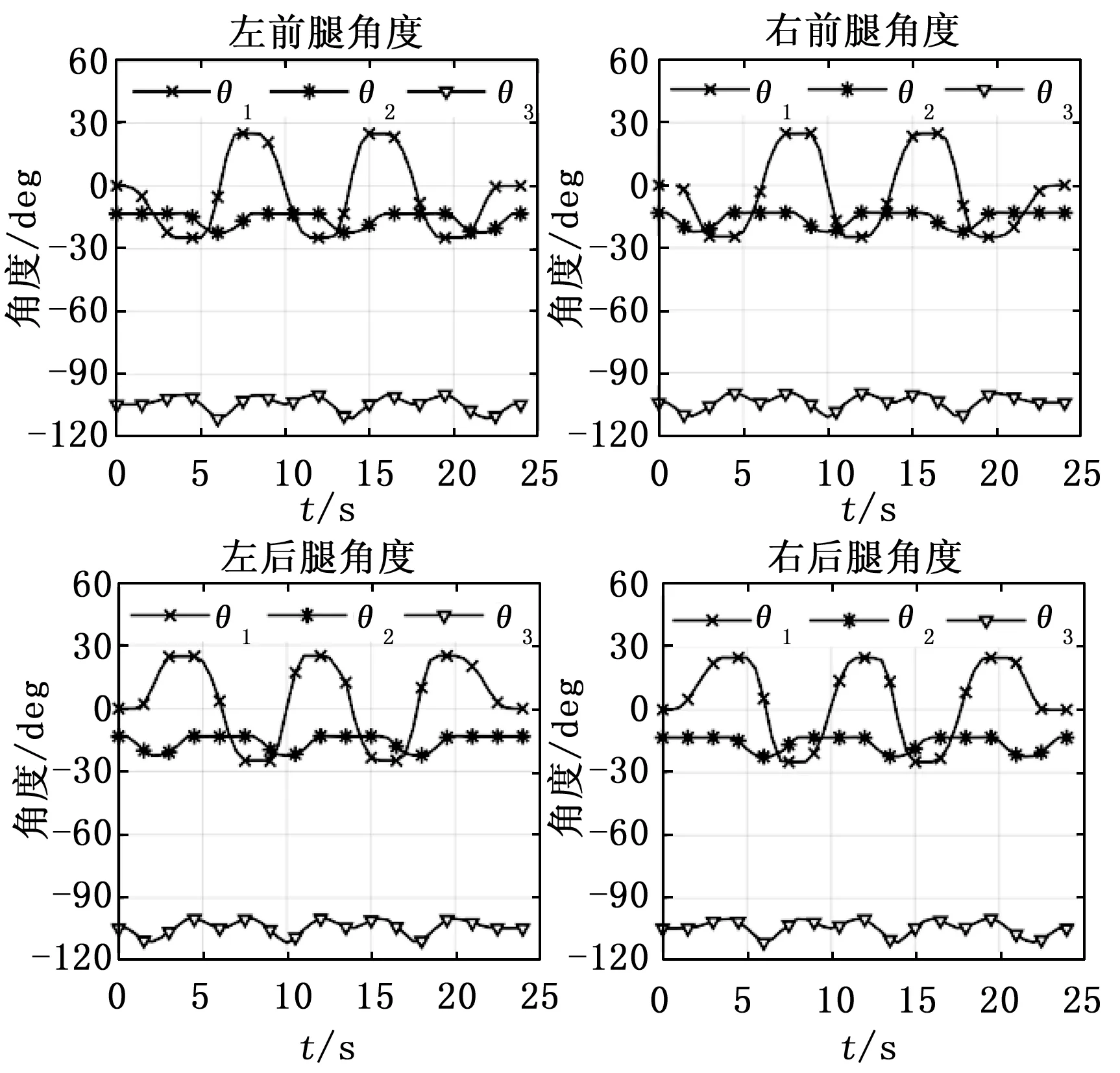
图14 机器人前进爬行运动时各腿关节角度
5 结束语
为了对爬游机器人足端轨迹进行合理规划,本文首先根据爬游机器人的整体结构研究并建立了机器人运动学数学模型;然后分析了四阶多项式和六阶多项式对机器人足端轨迹曲线的可控性,运用基于六阶多项式的机器人足端轨迹规划算法,解决了直线轨迹和曲线轨迹连接处的速度不连续问题,使机械腿在运动过程中更加柔顺;之后建立机械腿仿真模型,通过仿真验证了算法的有效性。最后利用爬游机器人实物样机在水池中稳定爬行运动,验证了本文所提出的高阶多项式机器人足端轨迹规划方法的有效性。

