基于VR设备中IMU的无手交互方法研究

张雁鹏,陈世均,高建勇

(苏州热工研究院有限公司 设备管理部，广东 深圳 518028 )

0 引言

虚拟现实(VR,virtual reality)设备是一种头戴式设备，允许用户通过显示立体视觉图像与三维虚拟现实环境进行交互。该设备可以分析用户的头部状态，并在虚拟现实世界中调整虚拟摄像机的位置，以增强沉浸感。随着VR技术的发展，基于这项技术的教育和培训越来越流行[1-7]。

使用虚拟现实进行教育和培训可以与使用二维计算机辅助教学模拟相媲美。在每一个层次的教育中，VR都有发挥作用的潜力，引导学习者获得新发现，激励、激发学习热情。学习者可以在学习环境中获得一种存在感、一种融入环境的感觉。在教育和培训中使用VR的优势可以总结为：

1) 沉浸式虚拟现实提供第一人称非象征体验，可以专门设计适应于帮助某个学生的学习材料；

2) 这些体验在常规教育中无法获得。

3) 这种体验构成了我们与外界日常互动的大部分，尽管学校更提倡第三人称的象征体验。

4)知识建构理论与虚拟现实技术的融合，使得学习能够通过虚拟世界中物体相对大小的操纵，通过传递其他不易察觉的信息源，以及通过具体化迄今为止无法表达的抽象概念来促进。

采用外部视觉跟踪设备对头部进行姿态测量和运动感知[8-9]，虽然具有很高的精度，但是无形之中增加了教学成本和场地使用的局限性。此外，还需要两种系统间的通信，难免会存在时间上的延迟。将低成本惯性测量单元(IMU，inertial measurement unit)与VR设备进行刚性连接，然后对人体头部姿态和运动状态进行测量的方式[10-11]，可以充分利用IMU中嵌入的加速度计、陀螺仪以及磁强计等传感器对姿态和运动信息进行感知，保证了可靠的精度，降低了成本，同时降低了设备使用的局限性，提高了使用的独立性。

在VR设备与用户的交互设计中，最流行的当属体感游戏的设计。在基于VR的体感射击游戏中，文献[12]中使用原地踏步走(WIP，walking-in-place)来模拟前进运动，这种方式的优点在于可以解放使用者的双手，正如文章标题中所示的“无手交互”，达到更加逼近真实体验的效果。大多数使用WIP方式交互的VR设备使用硬件(例如跑步机)进行步行运动识别[13-14]。近年来，仅使用移动VR设备中IMU的研究越来越多[15-18]。因此，可以借鉴VR体感射击游戏中WIP技术的应用，轻松实现教育培训中遇到的动态人机交互问题。

针对VR设备与使用者的动态交互问题，本文提出了将姿态感知与步态识别相结合的交互方法，来实现虚拟的靠近和躲避。首先，设计了基于间接扩展卡尔曼滤波器的姿态感知算法用于感知头部的姿态，该方法采用多传感器融合的方法，利用比力和地磁信息对姿态角误差进行外部观测，进而通过卡尔曼滤波器得到姿态误差角的最优估计量，最后对原始姿态进行补偿，实现了高的姿态测量精度；其次，由于原地踏步走时人体重心会有起伏，通过固定滑窗计算比力的峰值，并根据峰值大小和相邻峰值时间间隔进行静止和行走状态的识别；最终，将计算出的航向角和固定步长代入三角函数公式计算出虚拟运动的轨迹，模拟实现了前进与躲避障碍物。

1 姿态感知算法

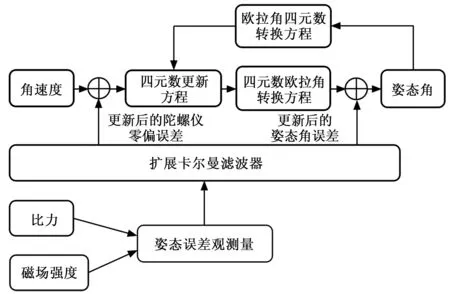
图1 测姿算法整体框图

1.1 扩展卡尔曼滤波器设计

EKF作为标准卡尔曼滤波器在非线性情况下的推广，其设计的关键在于状态方程(时间更新)和测量方程(测量更新)的推导。该滤波方法利用泰勒级数展开对非线性状态方程和非线性测量方程进行线性化，所以从本质上讲它也是一种线性卡尔曼滤波的方法，具体详见文献[20]。在本文中，我们使用它的间接形式，即先估计出系统状态的最优误差量，然后再对系统状态进行补偿。

1.1.1 系统误差状态模型

因为需要对姿态进行计算，所以我们设定系统状态向量xk包含3-D姿态角φk和陀螺仪零位偏移bω,k，因此有：

(1)

其中:姿态角φk可以通过四元数计算得到。那么，姿态角φ(包含俯仰角θ、滚转角γ、偏航角ψ)可以表示为：

(2)

其中:q0q1q2q3表示四元数矢量的4个元素。四元数可以表示为q=q0+q1i+q2j+q3k，其中q0表示四元数的实部或标量部分，而q1i+q2j+q3k表示虚部或矢量部分。

下一时刻的旋转四元数可以通过四元数更新方程[19]求得：

(3)

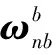
如果只考虑陀螺仪零偏误差bω,k，角速度真值ωk可由陀螺仪实际测量信号yk得到：

(4)

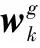
(5)

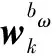
紧接着，利用EKF的间接形式，我们可以引入姿态测量系统状态向量xk的误差量δxk，最终对系统状态xk进行补偿。因此，系统的误差状态向量将包含6维元素，即:

δxk=[δφk,δbω,k]T

(6)

其中:δbω,k表示陀螺仪零位偏移误差，δφk表示姿态误差角。

根据文献[20]所述，要设计扩展卡尔曼滤波器的状态方程，首先写出误差状态量的微分方程，然后再将其离散化。那么，连续误差状态方程可以描述为：

(7)

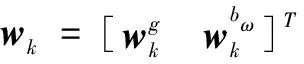
那么，离散化后的误差状态方程为：

(8)

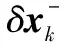
将离散状态转移矩阵Φk进行一阶泰勒级数展开(相当于将非线性模型线性化)，保留一阶项，那么有:

Φk=exp(Fc,kΔt)≈I6×6+Fc,kΔt

(9)

其中:Δt表示IMU的采样间隔。

1.1.2 系统误差测量模型

系统误差测量模型可以表示为：

zk=Hδxk+nk

(10)

其中:zk为误差测量向量；H为测量转移矩阵；nk为测量噪声的协方差矩阵。

假定人体运动的加速度远小于重力加速度，通过比力fk可以求得俯仰角和滚转角，那么有:

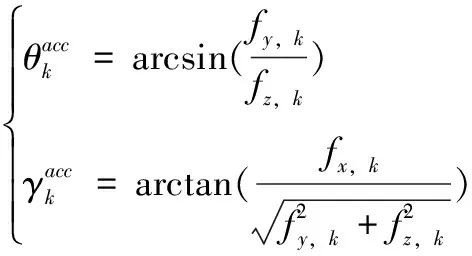
(11)

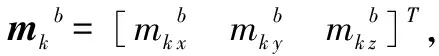
(12)

式中，n系下IMU的滚转角γk和俯仰角θk可以通过公式(11)求得。

由于地磁北极与地理北极不完全一致，定义地球表面任意点的地磁场强度矢量所在的垂直平面(地磁子午面)与地理子午面的夹角为地磁偏角(D)，不同地区对应有不同的磁偏角。因此地磁航向角可以表示为：

(13)

滤波器更新方程为：

(14)

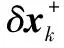
2 步态感知算法

我们利用比力模值来进行静止和行走行为的识别。比力模值的计算公式为：

(15)

其中:f表示比力矢量(比力表示加速度计测量到的包含重力加速度的加速度)，fx，fy，fz分别表示3个轴向的比力分量。

对计算所得的比力模值信号进行均值滤波，从而对信号进行平滑，减小运动时振动的影响。选取长度为N的滑窗，计算窗口中的最大值。当该最大值与重力加速度的绝对值小于某个范围时，则认为当前时间段内为静止状态；当大于这个范围且相邻两个满足条件的峰值的时间间隔大于某个时间时，则认为当前时间段内为行走状态，且在当前峰值状态时可以用来进行位置的更新。用公式可以表示为：

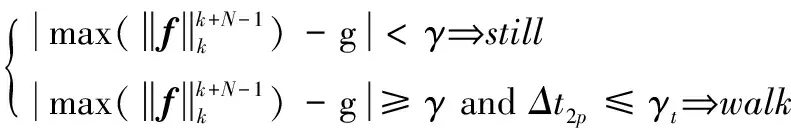
(16)

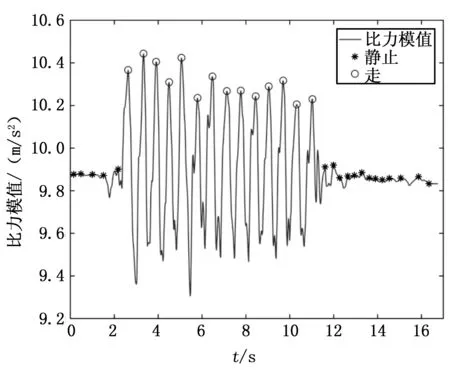
图2 静止和行走识别结果

3 虚拟轨迹计算

在计算虚拟路径时，仅在检测到比力模值峰值时，对位置进行更新。通过文中第二节提出的方法，可以判断出不同峰值时人体所处的运动状态。针对不同运动状态对应不同的位置更新公式，如下：

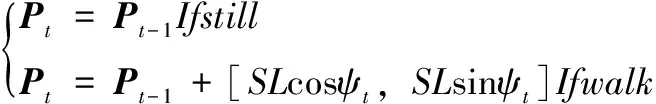
(17)

其中:P表示2D位置矢量；SL表示给定的步长，在本文中采用固定步长；t表示峰值所在的时间点。该公式可以解释为：当静止状态(still)时，说明人体没有移动，保持与上一峰值时相同的位置；当行走状态(walk)时，利用步长和航向角，根据三角函数关系计算出该时刻的位置。

4 实验结果与分析

为了验证本文提出算法的有效性，本文设计了多姿态运动实验和模拟交互实验。多姿态运动实验包括蛇形、俯仰、晃动、转圈和倒退5种姿态进行运动实验。模拟交互实验包括模拟直线行走和模拟在直线行走过程中躲避障碍物两种实验。使用的IMU是SBG公司生产的IG-500N，包含三轴加速度计、三轴陀螺仪和三轴磁强计。其中，加速度计的量程为±5 g，零偏稳定性为±4 mg；陀螺仪的量程为±300°，零偏稳定性为±0.1°/s；磁强计量程为±1.2 Gauss，零偏稳定性为±0.5 mGauss。

4.1 多姿态运动实验

多姿态运动实验的测试地点为室内直线走廊。该实验的具体过程为：测试者将IMU佩戴在头部的额头位置，依次按照蛇形(原地从左转到右再转到左来模拟蛇形运动)、俯仰(头部先向前倾，进而向后仰)、晃动(左右晃动头部)、转圈(原地转圈)和倒退(原地身体边后倾边原地踏步来模拟倒退运动)5种姿态进行原地运动。将IMU内部集成的商业姿态感知算法实时输出的姿态角和本文提出的姿态感知算法解算出的姿态角画在同一坐标系中进行对比，如图3所示。图中，深色线表示本文算法解算出的姿态角；浅色线表示IMU直接输出的姿态角。可以看出，两条线基本重合。

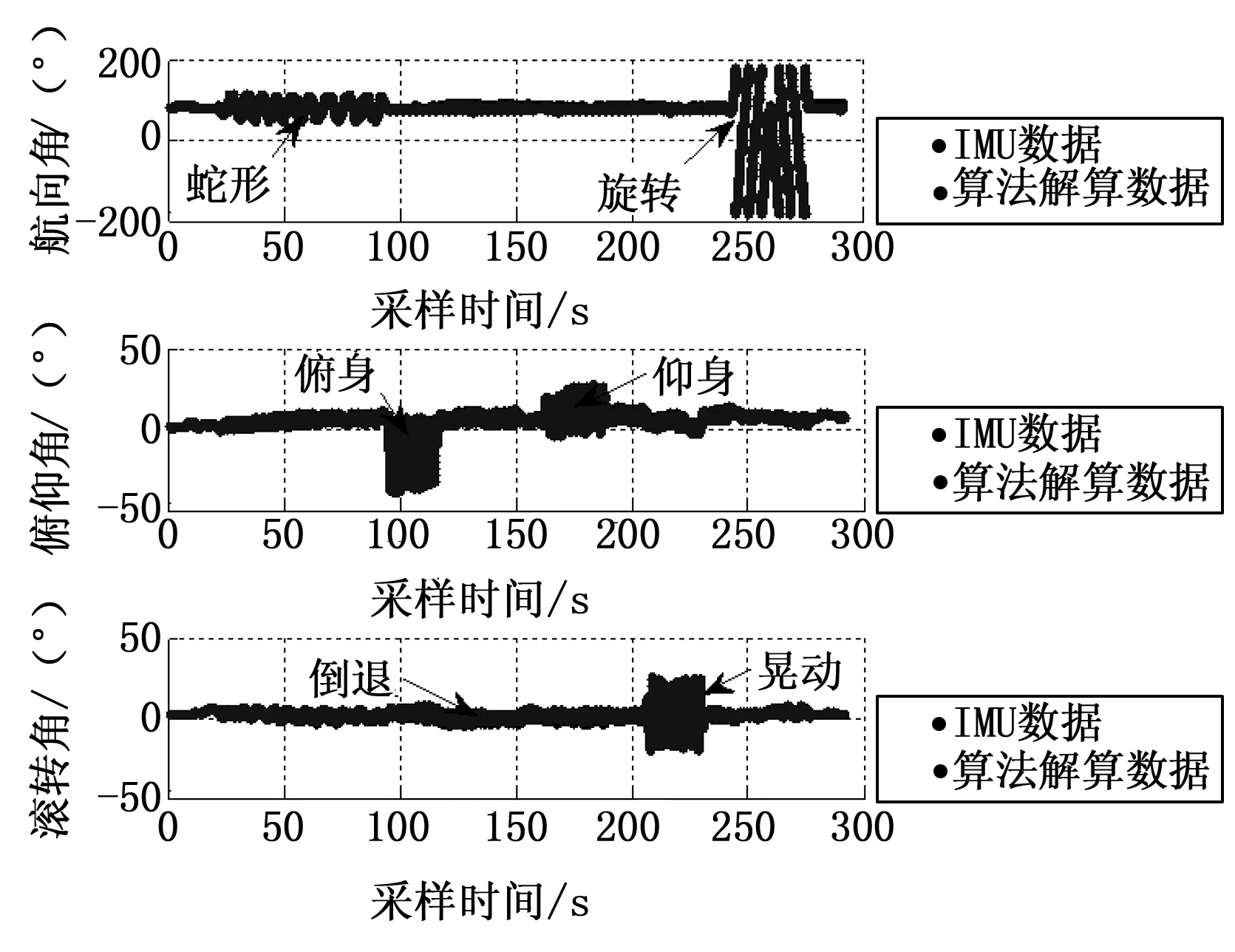
图3 多姿态运动解算结果对比

4.2 模拟交互实验

为了检验提出的交互方法的有效性，模拟交互实验包含模拟直线行走和模拟在直线行走过程中躲避障碍物两种实验。IMU的安装位置为额头处。具体的实验过程为：(1)测试者佩戴IMU面朝一个方向不断原地踏步来模拟在现实世界中的直线行走，本文提出的系统计算出的路径如图4所示；(2)测试者面朝一个方向通过原地踏步走模拟直线行走，同时不同改变朝向来模拟躲避前方障碍物，然后恢复与起始朝向相同的方向向来实现沿原轨迹继续直线行走，所提系统的计算结果如图5所示。

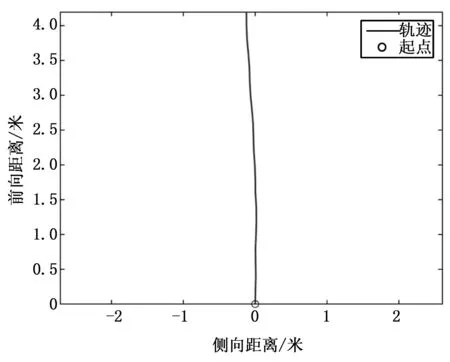
图4 模拟直线行走实验结果

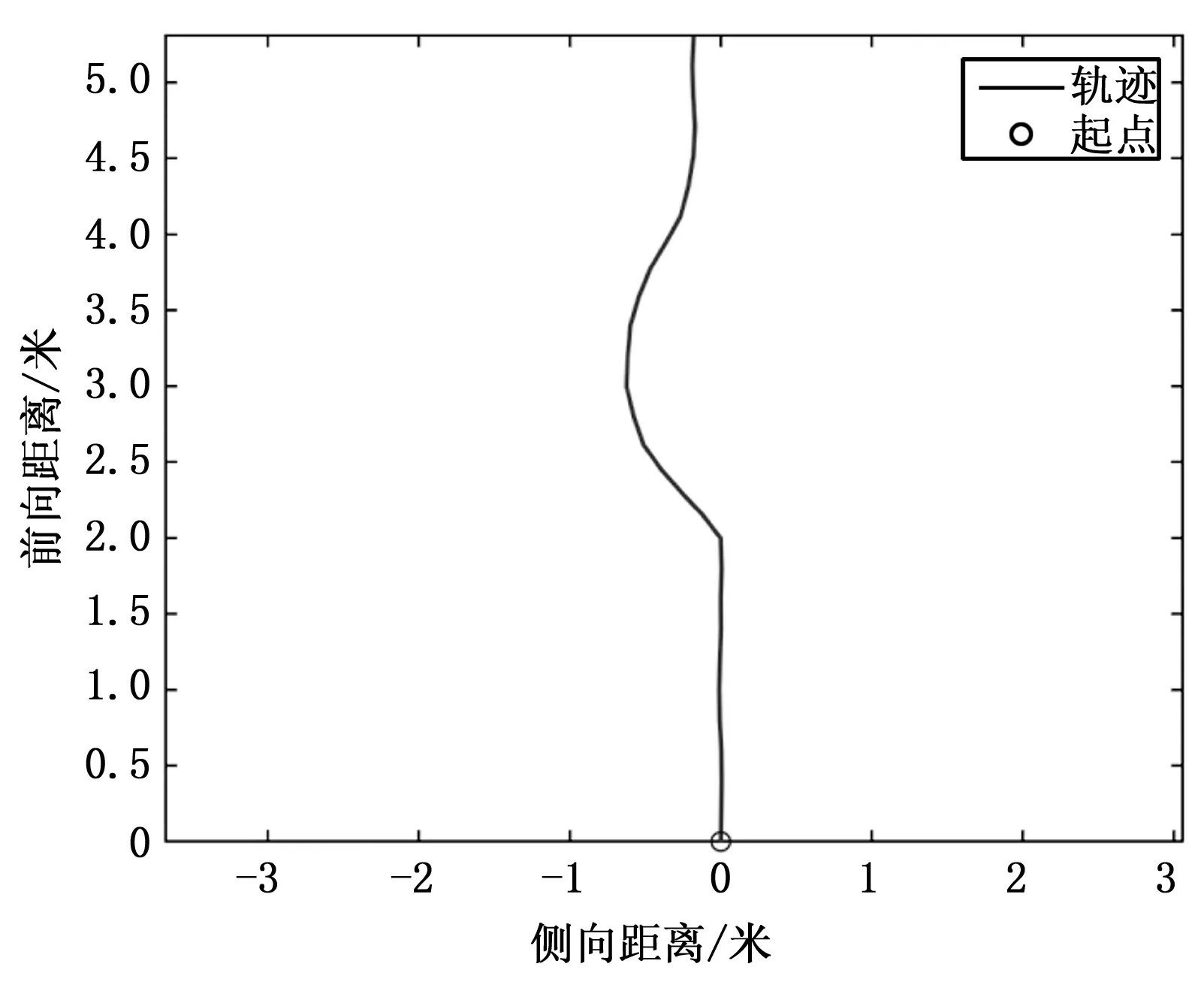
图5 模拟避障实验结果

4.3 结果分析

如图3中结果显示，在多种运动状态下，本文提出姿态算法可以精确的计算出相应的姿态信息，同时本文所提算法与IMU自带的商业解算程序计算的结果基本重合，通过计算得出与商用惯性测量单元提供的姿态角具有1.1×10-2°的平均姿态偏差，从而最终证明本文提出的姿态感知算法的有效性，可以精确有效的解算出人体头部的真实姿态。

从模拟交互实验中两组实验的结果(如图4～5所示)可以看出，本文提出的交互方法能够很好的模拟实现人体的前进和在前进的过程中躲避前方的障碍物。将本文所提算法部署到VR设备中，能够有效的帮助使用者在体验VR的同时，实现与VR视频中对象的靠近与躲避，从而实现人与设备之间的交互，达到身临其境的沉浸式效果。

但是该算法也有不足的地方，在未来的工作中，期望能够加入更多的交互动作，比如说后退或者侧行，来进一步丰富体验者与VR设备间的交互方式。

5 结束语

针对VR设备与使用者的动态交互问题，本文提出了姿态感知与步态识别相结合的交互方法，实现了靠近或躲避VR视频中的对象。实验证明，提出的姿态感知算法可以有效的计算出使用者头部的姿态，且具有较高的解算精度，与商用惯性测量单元提供的姿态角基准相比具有1.1×10-2的平均姿态角偏差；提出的步态识别算法可以有效的识别出人体的静止与行走状态；所提出的两者结合的交互方法，可以有效的实现虚拟的靠近与躲避。在未来的工作中，期望能够加入更多的交互动作，比如说后退或者侧行。