四足机器人足端复合轨迹运动特性研究*
齐晓宇,王赫莹,郭忠峰
(1.沈阳工业大学机械工程学院,辽宁 沈阳 110870;2.沈阳工业大学辽宁省智能制造与工业机器人重点实验室,辽宁 沈阳 110870)
0 引言
与更适应平整地面运动的轮式移动机器人以及履带式移动机器人相比,腿足式移动机器人运动更灵活,具备能通过复杂崎岖地形的能力[1],其中四足机器人已经成为国内外机器人研究领域的热点,更强的地形适应能力是四足机器人未来的发展大趋势[2]。合理的足端运动轨迹规划不仅能保证四足机器人运动效率,还能提高机器人运动平稳性[3],因此针对四足机器人足端轨迹规划和运动特性进行研究,具有十分重要意义。
国内外对四足机器人的足端轨迹规划研究,基于机器人在平地运动平稳性上考虑多选用简单的摆线函数[4]、多项式函数[5]、椭圆函数[6]等完整统一的曲线规划足端轨迹。本文将综合考虑机器人运动平稳性、运动效率、地形适应能力等方面因素,对机器人足端轨迹进行设计,以运动效率较高的对角步态运动方式在Adams和matlab/simulink仿真环境搭建机器人模型和虚拟模型控制系统,研究机器人在该足端轨迹规划下的运动特性。
1 四足机器人模型介绍
1.1 四足机器人模型结构
本文以前肘后膝式的四足机器人为对象,机器人每条腿具有髋关节前摆、侧摆和膝关节前摆3个主动自由度,整体共有12个自由度,机器人的控制方法采用虚拟模型控制方法,研究机器人以运动效率较高的对角步态在平地和崎岖地形的运动特性。
如图1所示,机器人大腿长度为l1,小腿长度为l2,机器人前后髋关节距离的一半为A,左右髋关节距离的一半为B,设机器人质心坐标为{O},以右前腿为例设其髋关节坐标为{A},右前腿足端坐标系为{Q},髋关节侧摆角度为θ0,前摆角度为θ1,膝关节前摆角度为θ2。足端在髋关节的坐标系{A}下的位置表示为P(x,y,z),其中x代表前进方向,y代表侧向,z代表竖直方向,则方程式如下:
x=-l1cosθ1-l2cos(θ2+θ1)
y=l1cosθ0sinθ1+l2cosθ0sin(θ2+θ1)
z=-l1sinθ1cosθ1-l2sinθ0sin(θ2+θ1)
(1)
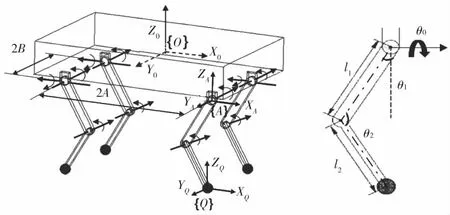
图1 四足机器人模型和单腿模型
通过对式(1)中的髋关节前摆角度和侧摆角度以及膝关节的前摆角度进行求导并转置可得到力雅可比矩阵:
(2)
其中,c0=cosθ0,s0=sinθ0;
c1=cosθ1,s1=sinθ1;
c2=cosθ2,s2=sinθ2;
c12=cos(θ1+θ2),s12=sin(θ1+θ2)。
1.2 四足机器人控制方法
虚拟模型控制方法(VMC,Virtual model control)是直觉控制方法的一种,其控制原理为在机器人上的作用点与外部期望运动轨迹之间通过虚拟假想的弹簧、阻尼器等构件连接,使其产生好像真实构件存在产生的虚拟力实现类似实际构件驱动的运动状态[8]。
对于四足机器人的控制来说就是足端和髋关节之间建立虚拟的弹簧元件和阻尼元件,生成机器人各腿部关节所需的力矩驱动机器人腿部运动从而达到跟随期望速度和位移的目的。
设控制膝关节和髋关节的力矩为:
τ=JTf
(3)
代入(2)式可得:
(4)
其中,τh1、τh2、τh3分别代表髋关节侧摆和前摆力矩和膝关节力矩,Fhx、Fhy、Fhz分别代表虚拟的弹簧和阻尼构件牵引机器人足端按照期望的足端轨迹运动的XQ、YQ、ZQ三个方向上的虚拟力[9],其本构方程为:
(5)
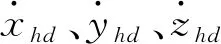
2 四足机器人足端轨迹规划
2.1 足端轨迹规划要求
不考虑机器人的视觉处理系统,对四足机器人在崎岖地形行走设计一种足端轨迹,设计目标主要有:
①机器人能顺利越过高度不超过足端最大抬腿高度80%的不规则障碍物。
②机器人能够适应由地面高度变化引起机身翻转,即质心处的横滚角、俯仰角以及偏移角±0.1 rad内的波动,并在完全通过障碍后恢复平衡。
③机器人通过障碍时侧向偏移位移不应超过前进位移的7%,以保证机器人的运动效率。
将机器人的足端运动轨迹分为起步、跨步、落地三个阶段进行设计,整体的运动轨迹为:机器人足端收腿运动从P0到P1,然后竖直抬腿到P2,再从P2跨步运动经过抬腿最高点P3后到P4完成跨步运动,从P4运动到P6完成竖直落地运动,机器人的足端行走轨迹如图2所示。
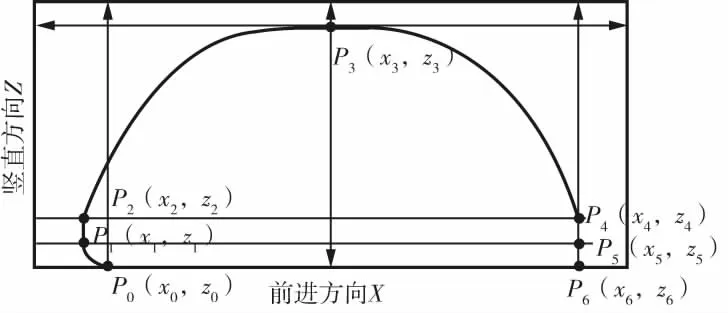
图2 足端行走轨迹
2.2 足端轨迹规划起步阶段
足端轨迹在摆动相起步时,模仿生物狗的足端运动轨迹,先向后收腿再竖直抬起然后进行跨步,可在起步阶段绕过未知突出障碍物;向后收腿并竖直抬起一定高度后再进行跨步向前,可防止机器人足端在起步阶段就碰到障碍,导致机器人足端运动突变引起机器人倾覆,如图3所示。
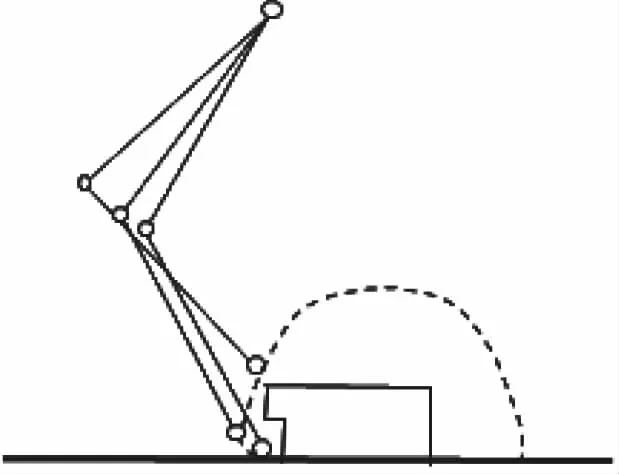
图3 起步阶段绕过凸出障碍的足端轨迹示意图

因此添加以下约束:
(6)
足端起步阶段的轨迹采用五次多项式曲线拟合,设起步轨迹方程为:
x=ft5+et4+dt3+ct2+bt+a
(7)
z=lt5+kt4+jt3+it2+ht+g
(8)
其中,a、b、c、d、e、f为前进方向轨迹方程的系数,g、h、i、j、k、l为竖直方向轨迹方程系数,带入以上约束(6),解得起步阶段足端轨迹方程:
(9)
(10)
2.3 足端轨迹规划跨步阶段
选择复合摆线曲线规划作为跨步阶段足端轨迹,其主要优势有以下两点:
①复合摆线曲线平滑流畅,可避免机器人在跨步运动时由于规划的足端轨迹突变引起运动不稳定。
②复合摆线曲线规划的足端运动到最大抬腿高度时曲线变化较平缓,与其他带尖顶的足端轨迹相比,可以在障碍物不高于规划的最大抬腿高度的情况下,尽可能的跨越障碍物,如图4所示。
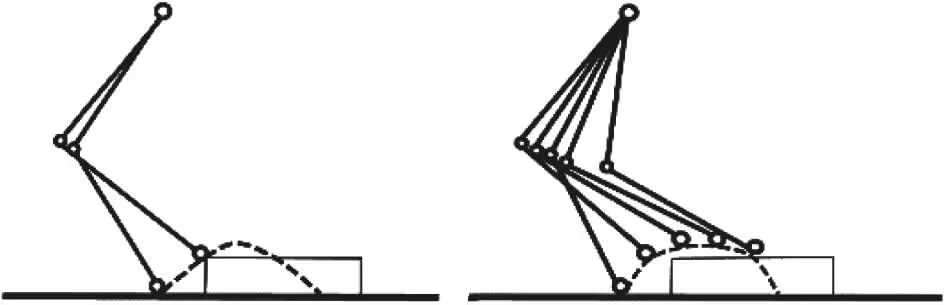
图4 跨步阶段越过障碍的足端轨迹对比示意图
(11)
设跨步阶段的复合摆线轨迹曲线前进加速度方程为:
(12)
通过积分得出速度方程:
(13)
再次积分得到位移方程:
(14)
分别代入以上约束(11),可得跨步阶段前进方向足端轨迹方程为:
(15)
同理,可得跨步阶段竖直方向足端轨迹方程:
(16)
2.4 足端轨迹整体规划
最后落地部分,规划足端以一定高度跨步到要求位置后竖直下落,使其能够适应足端提前落地或者滞后落地的情况,可尽量避免机器人落地打滑的发生。从跨步运动结束后,机器人足端的前进方向的位移、速度和加速度均为零,竖直方向采用同起步阶段对称的五次多项式曲线轨迹规划。
综上所述,四足机器人摆动相足端轨迹规划前进方向和竖直方向的数学方程式为:
(17)
(18)
令足端轨迹的步长L为0.08 m,抬腿高度为0.045 m,摆动相运动周期为1 s,前进方向起始位置在距离跨步起点的0.0025 m处,将轨迹方程相关程序在matlab软件中运行得到前进方向和竖直方向位移曲线和速度曲线如图5(a)、(b)、(c)、(d)所示,位移曲线和速度曲线均平滑流畅无较大突变。
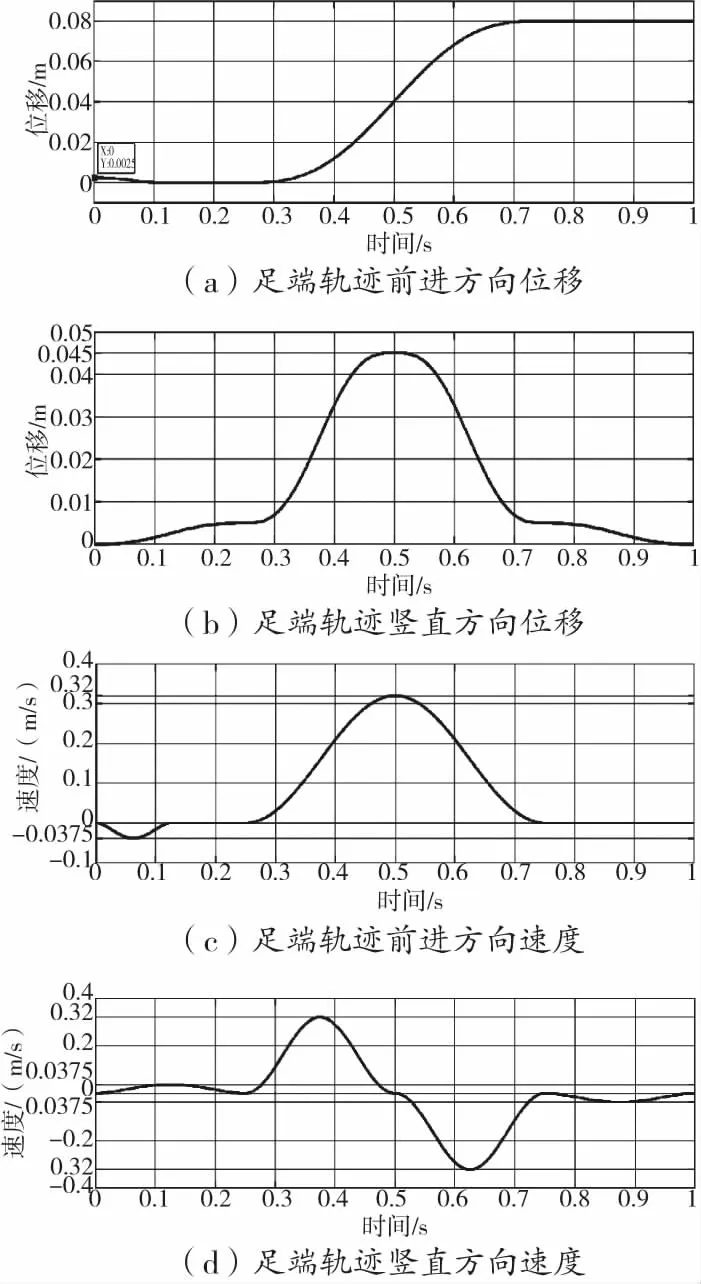
图5 足端轨迹主要数据曲线
由于机器人在支撑相时,足端不离开地面,只有一个足端相对髋关节向后方向的运动,因此无需对足端竖直方向轨迹规划,前进方向的轨迹与摆动相的前进方向相反,则有:
(19)
zf(t)=0
(20)
其中Th为支撑相周期。
3 四足机器人仿真试验验证
3.1 四足机器人仿真环境介绍
为检验机器人以设计的足端轨迹规划运动特性,搭建机器人分别在平地上和崎岖地形的以目前使用较多的五次多项式曲线规划足端轨迹与设计的足端轨迹进行运动仿真实验。
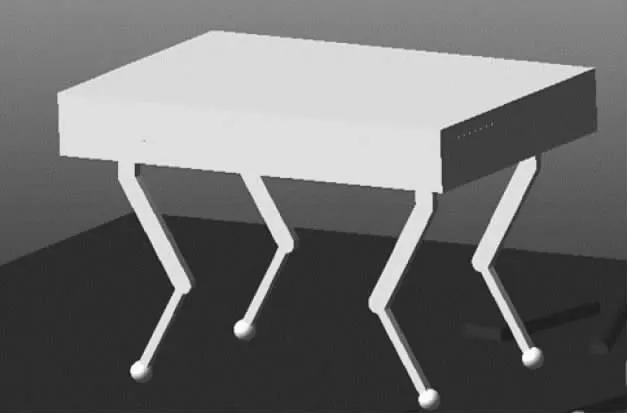
图6 机器人模型图
在Adams软件完成机器人的运动模型搭建,如图6所示,机器人的控制系统在matlab/simulink下搭建,并进行联合仿真。机器人结构参数如表1所示,躯干重量分布于四个髋关节位置和躯干几何中心位置,运动模式为对角小跑步态。

表1 机器人结构参数表
3.2 四足机器人的平地运动仿真
在Adams软件中的平地运动环境设置两种足端轨迹步长均为0.07 m,抬腿高度为0.04 m,运动周期为2 s。以下仿真数据中实线和虚线分别代表设计的足端轨迹和五次多项式曲线足端轨迹的机器人运动数据曲线,如图7(a)中,两种足端轨迹规划的机器人运动在30 s后前进方向的位移几乎一致;如图7(b)所示,以五次多项式曲线足端轨迹运动的机身质心俯仰角的波动大致在-0.013~0.015 rad,以设计的足端轨迹运动的机身质心俯仰角的波动大致在-0.015~0.022 rad;如图7(c)所示,以五次多项式曲线足端轨迹运动的机身质心横滚角的波动在-0.01~0.003 rad,以设计足端轨迹运动的机身质心横滚角的波动在-0.012~0.005 rad。
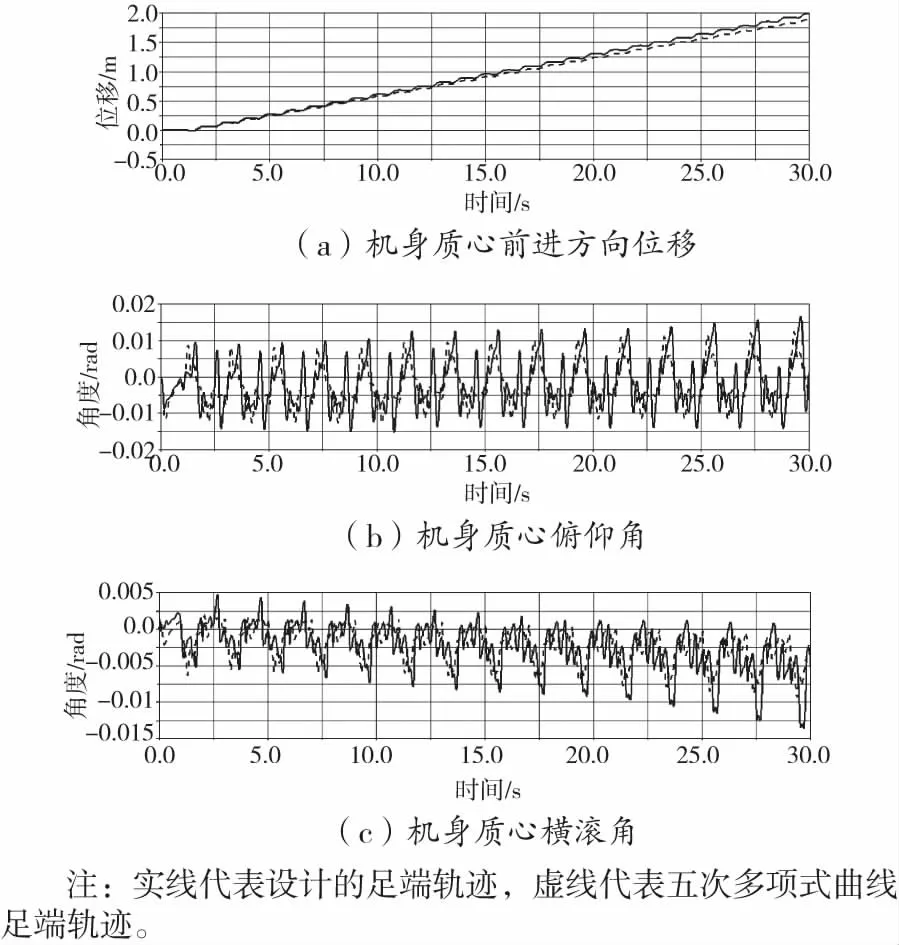
图7 机器人平地行走的仿真实验主要数据曲线
以上仿真数据证明,以设计的足端轨迹规划运动和五次多项式曲线规划运动的机器人在平地上能保证一定运动平稳性,且采用设计的足端轨迹并没有因为是分段式函数不如完全使用五次多项式曲线规划的行走曲线更平滑,而导致运动效率下降,机器人运动平稳性也没有受到过大影响。
3.3 四足机器人的崎岖地形仿真
崎岖地形多是由高低不平的地面和未知的可移动障碍物组成,因此通过Adams软件设置多个高度不同的凸台和可移动的球体随机分布在机器人运动范围内模拟崎岖地形,如图8所示。其中凸台高度最大的为0.055 m,最小的为0.03 m,可移动球体直径最高为0.055 m,最小为0.03 m,设置两种足端轨迹步长为0.07 m,抬腿高度为0.06 m,运动周期为2 s。

图8 仿真环境下建立的崎岖地形
图9为机器人通过崎岖地形时在0 s、10 s、28 s、44 s时的仿真截图,机器人总共前进了约3 m,历时50 s,在44 s左右完全通过了仿真环境中所有障碍物。
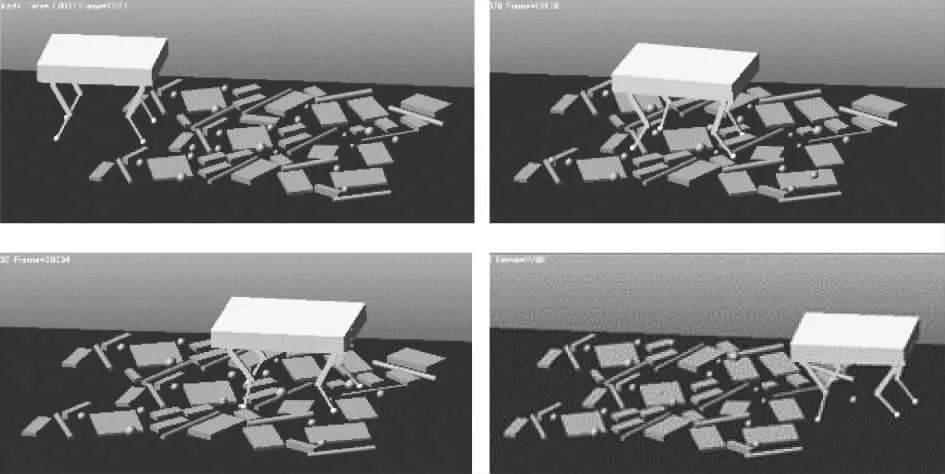
图9 机器人通过崎岖地形的仿真截图
图10(a)为四足机器人在崎岖地形运动时两种足端轨迹运动的前进方向位移,两者差距不大。由于机器人受崎岖地形中的凸台影响,不可避免的发生侧向运动的偏移,如图10(b)所示,机器人采用设计的足端轨迹通过障碍时的侧向偏移位移约为前进位移的6.7%,随后便保持稳定不再增大。而五次多项式足端轨迹通过障碍时的侧向偏移位移约为前进位移的9.0%。如图10(e)的数据曲线显示五次多项式足端轨迹机身质心偏移角,明显大于设计的足端轨迹的质心偏移角,并在完全通过障碍后仍继续增大。
如图10(c),在机器人完全通过障碍以后,设计的足端轨迹的机器人整体恢复平衡质心俯仰角逐渐稳定在±0.015 rad范围内,而采用五次多项式曲线的足端轨迹的机器人质心俯仰角在-0.02~0.025 rad范围内波动。另外观察图10(d)的数据曲线波动情况,采用五次多项式曲线的足端轨迹运动的机身质心横滚角在通过崎岖地面以后仍逐渐变大,容易导致机器人运动侧翻,而采用设计的足端轨迹运动的横滚角在通过崎岖地面以后则逐渐稳定在±0.01 rad附近。
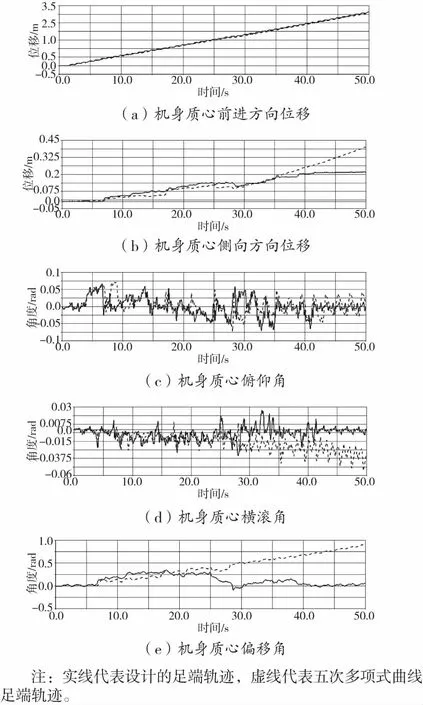
图10 机器人崎岖地面行走的仿真实验主要数据曲线
综上所述,可以证明机器人采用设计的足端轨迹能更好地抵御崎岖地形对机器人运动的干扰,保证一定的运动平稳性和方向准确性,达到了足端轨迹规划预期要求。
4 结论
本文提出了一种可适应崎岖地形的复合足端轨迹规划方法,对设计的足端轨迹的运动特性进行分析研究,并且在matlab/simulink与Adams联合仿真环境下采用设计的足端轨迹与五次多项式足端轨迹分别在平地、崎岖环境下进行运动情况对比,仿真结果显示采用以五次多项式轨迹运动和以设计的足端轨迹运动的机器人均能顺利通过平地和障碍物不超过足端轨迹步长80%的崎岖地面,在平地上运动时以设计的足端轨迹运动与以五次多项式轨迹运动相比平稳性稍逊,在崎岖地形上以设计的足端轨迹运动的机器人能够适应横滚角、俯仰角以及偏移角±0.1 rad内的波动,并在完全通过障碍后恢复平衡,侧向偏移位移为前进位移的6.7%,而以五次多项式轨迹运动在完全通过障碍后并未恢复到平衡状态,侧向偏移位移为前进位移的9.0%,因此可以证明以设计的足端轨迹运动的机器人能更好地抵御崎岖地形的干扰,具有更好的运动平稳性和地形适应能力。

